Effect of Ambient Parameters on the Temperature Distribution of Photovoltaic (PV) Modules
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermal Modeling and Finite Element Analysis (FEA)
- is the Prandtl number
- (N-s/m2) is the dynamic viscosity
- . (kJ/kg-K) is the specific heat capacity
- k (W/m-K) is the thermal conductivity
- β (1/K) is the coefficient of thermal expansion
- ν (m2/s) is the kinematic viscosity
2.2. Experimental Set-Up
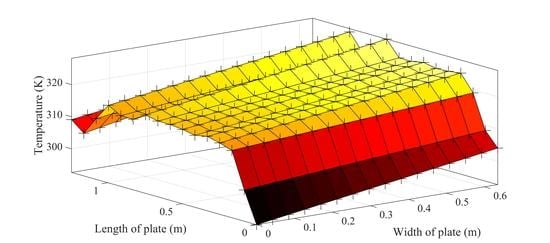
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tonui, J.; Tripanagnostopoulos, Y. Air-cooled PV/T solar collectors with low cost performance improvements. Sol. Energy 2007, 81, 498–511. [Google Scholar] [CrossRef]
- Armstrong, S.; Hurley, W. A thermal model for photovoltaic panels under varying atmospheric conditions. Appl. Eng. 2010, 30, 1488–1495. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Clugston, V.; Basore, P.A. Modelling free-carrier absorption in solar cells. Prog. Photovolt. 1997, 52, 29–239. [Google Scholar] [CrossRef]
- Vogt, M.R.; Holst, H.; Winter, M.; Brendel, R.; Altermatt, P.P. Numerical Modeling of c-Si PV Modules by Coupling the Semiconductor with the Thermal Conduction, Convection and Radiation Equations. Energy Procedia 2015, 77, 215–224. [Google Scholar] [CrossRef] [Green Version]
- Siddiqui, M.U.; Arif, A.; Arif, A.F.M. Electrical, thermal and structural performance of a cooled PV module: Transient analysis using a multiphysics model. Appl. Energy 2013, 112, 300–312. [Google Scholar] [CrossRef]
- Zhou, J.-C.; Zhang, Z.; Liu, H.-J.; Yi, Q. Temperature distribution and back sheet role of polycrystalline silicon photovoltaic modules. Appl. Eng. 2017, 111, 1296–1303. [Google Scholar] [CrossRef]
- Zhou, J.; Yi, Q.; Wang, Y.; Ye, Z. Temperature distribution of photovoltaic module based on finite element simulation. Sol. Energy 2015, 111, 97–103. [Google Scholar] [CrossRef]
- Assila, H.; Essadiqi, E.; Faqir, M.; Meziane, M.; Ghanameh, F.; Ahzi, S. Numerical simulation of photovoltaic panel thermal condition under wind convection. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 14–17 November 2016. [Google Scholar]
- Jones, A.; Underwood, C. A thermal model for photovoltaic systems. Sol. Energy 2001, 70, 349–359. [Google Scholar] [CrossRef]
- Hammami, M.; Torretti, S.; Grimaccia, F.; Grandi, G. Thermal and Performance Analysis of a Photovoltaic Module with an Integrated Energy Storage System. Appl. Sci. 2017, 7, 1107. [Google Scholar] [CrossRef]
- Dubey, S.; Tiwari, G. Thermal modeling of a combined system of photovoltaic thermal (PV/T) solar water heater. Sol. Energy 2008, 82, 602–612. [Google Scholar] [CrossRef]
- Akhsassi, M.; El Fathi, A.; Erraissi, N.; Aarich, N.; Bennouna, A.; Raoufi, M.; Outzourhit, A. Experimental investigation and modeling of the thermal behavior of a solar PV module. Sol. Energy Mater. Sol. Cells 2018, 180, 271–279. [Google Scholar] [CrossRef]
- Holman, J.P. Heat Transfer, 10th ed.; The McGraw-Hill Companies: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Nateri, A.S.; Ebrahimi, F.; Sadeghzade, N. Evaluation of yarn defects by image processing technique. Optik 2014, 125, 5998–6002. [Google Scholar] [CrossRef]
- Russ, J.C.; Woods, R.P. The image processing handbook. J. Comput. Assist. Tomogr. 1995, 19, 979–981. [Google Scholar] [CrossRef]
- Aghaei, M.; Grimaccia, F.; Gonano, C.A.; Leva, S.; Gonano, C. Innovative Automated Control System for PV Fields Inspection and Remote Control. IEEE Trans. Ind. Electron. 2015, 62, 7287–7296. [Google Scholar] [CrossRef]











| DUNA SOLAR (Module A) | SOLARWATTS (Module B) | SOLAREX (Module C) | RWE SCOTT SOLAR (Module D) | |
|---|---|---|---|---|
| Parameter | a-Si (G-G) | mc-Si (G-G) | pc-Si (G-T) (60Wp) | pc-Si (G-T) (105Wp) |
| Pmax (Wp) | 40 | 165 | 60 | 105 |
| Module Area (m2) | 0.791 | 1.62 | 0.564 | 0.826 |
| Temp. coeff. of power | −0.47%/°C | −0.40%/°C | −0.47%/°C | −0.47 %/°C |
| Stratigraphy | Glass-EVA-CELL-EVA-Glass (No frame) (G-G) | Glass-EVA-CELL-EVA-Glass (No frame) (G-G) | Glass-EVA-CELL-EVA-Tedlar (With frame) (G-T) | Glass-EVA-CELL-EVA-Tedlar (With frame) (G-T) |
| Parameter | Specification |
|---|---|
| TemperatureRange | −40 to 500 °C |
| Spectral range | 8–13 μm |
| Emissivity | 0.1–1.00 |
| Basic accuracy | ±2% or ± 2 °C |
| A/D Resolution | 14 bits |
| Response time | 150 ms |
| Detector | Microbolometer |
| Focusing range | 30 cm to infinity |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atsu, D.; Dhaundiyal, A. Effect of Ambient Parameters on the Temperature Distribution of Photovoltaic (PV) Modules. Resources 2019, 8, 107. https://doi.org/10.3390/resources8020107
Atsu D, Dhaundiyal A. Effect of Ambient Parameters on the Temperature Distribution of Photovoltaic (PV) Modules. Resources. 2019; 8(2):107. https://doi.org/10.3390/resources8020107
Chicago/Turabian StyleAtsu, Divine, and Alok Dhaundiyal. 2019. "Effect of Ambient Parameters on the Temperature Distribution of Photovoltaic (PV) Modules" Resources 8, no. 2: 107. https://doi.org/10.3390/resources8020107
APA StyleAtsu, D., & Dhaundiyal, A. (2019). Effect of Ambient Parameters on the Temperature Distribution of Photovoltaic (PV) Modules. Resources, 8(2), 107. https://doi.org/10.3390/resources8020107