Approaching Optimal Nonlinear Dimensionality Reduction by a Spiking Neural Network
Abstract
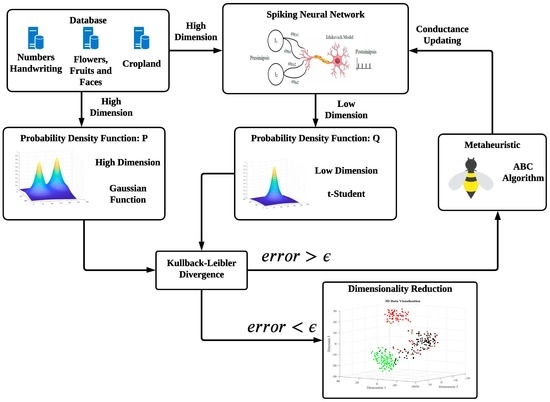
:1. Introduction
2. Main Topics
2.1. Dimensionality Reduction
2.2. Internet of Things
2.3. Edge Computing
2.4. Pre-Training Concept
2.5. Edge Computing Advantages by Using Neuromorphic Systems
- Energy efficiency: NS are more suitable than general-purpose computing hardware. The expected difference is several orders of magnitude.
- Low latency: NS surpass at processing continuous streams of data, reducing the delay to accomplish intelligent tasks.
- Adaptive processing: NS can adapt to changes in context.
- Rapid learning or adaptation: NS show capabilities beyond most standard artificial intelligence systems.
- The Artificial Bee Colony (ABC) algorithm is a gradient-free optimizer that conveniently replaces the STDP rule and backpropagation-based algorithms.
- The loss function in the t-distributed Stochastic Neighbor Embedding (t-SNE) method can act as the objective function in the ABC algorithm.
- The training phase is guided by the objective function of the ABC algorithm.
- The trained spiking neural network achieves efficiently a nonlinear dimensionality reduction, which is suitable for either task: reducing memory size or classifying complex data.
2.6. Metaheuristic Optimization
| Algorithm 1 ABC Pseudocode. |
|
| Algorithm 2 Employed Bees’ Labor Pseudocode (Modified from [15]). |
|
| Algorithm 3 Onlooker Bees’ Labor Pseudocode (Modified from [15]). |
|
| Algorithm 4 Scout Bees’ Labor Pseudocode (Modified from [15]). |
|
2.7. The T-Sne Machine Learning Method
3. Topics Related to Preparing Experiments
3.1. Neuron Model Used in This Work
3.2. Spiking Neural Network Architecture Used in This Work
3.3. Databases
3.4. Training Phase Strategy
4. Experimental Results
4.1. Relative Quality of Efficiency by Mse Evaluations
- MSE-1: Spiking versus Reference. Measures the deviation of the spiking network versus a reference neural network.
- MSE-2: Random versus Reference. Measures the deviation of the random distances versus a reference neural network.
4.2. Quality Measurement by the Co-Ranking Matrix
4.3. Handwriting Numbers Experiment
4.4. Images Experiment
4.5. Croplands Experiment
4.6. Discussion
- The numerical evaluation of the centers of the classes, i.e., Dimension 1, Dimension 2, and Dimension 3 in Figure 6, Figure 10, and Figure 14, by both the reference and spiking networks follow the same trend pattern. This proves that the spiking networks reproduce a performance near to the reference network.
- The MSE-1 and MSE-2 values are reported graphically in Figure 7, Figure 11, and Figure 15 and, whose comparisons follow the premises, P1 and P2. Their statements are below.
- P1. MSE-1 can compare the results provided by the experimental spiking network with the set of the expected results produced by a continuous sigmoid neuron network. MSE-1 should be relatively small.
- P2. MSE-2 can compare the results provided by a no correlated network with the set of the expected results produced by a continuous sigmoid neuron network. MSE-2 should be relatively large.
Comparing MSE-1 with MSE-2 leads to find that MSE-1 is always lower than MSE-2. This point proves that the efficiencies by all the SNNs are acceptable. - The graphical results in Figure 8, Figure 12, and Figure 16 show co-ranking matrices for all the experiments. The pairs Spiking/Reference Network have nearly the same trace. In addition, the third trace due to the numeric t-SNE was presented as the theoretical case, whose saturation is the same as the spiking and reference networks. The evaluation at this point demonstrates that the quality of the spiking networks are satisfactory.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, W.; Lu, J.; Li, X.; Chen, L.; Liu, K. Rethinking Motivation of Deep Neural Architectures. IEEE Circuits Syst. Mag. 2020, 20, 65–76. [Google Scholar] [CrossRef]
- Roy, K.; Jaiswal, A.; Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 2019, 575, 607–617. [Google Scholar] [CrossRef]
- Wang, X.; Lin, X.; Dang, X. Supervised learning in spiking neural networks: A review of algorithms and evaluations. Neural Netw. 2020, 125, 258–280. [Google Scholar] [CrossRef] [PubMed]
- Bouvier, M.; Valentian, A.; Mesquida, T.; Rummens, F.; Reyboz, M.; Vianello, E.; Beigne, E. Spiking neural networks hardware implementations and challenges: A survey. Acm J. Emerg. Technol. Comput. Syst. (JETC) 2019, 15, 1–35. [Google Scholar] [CrossRef]
- Ojha, V.K.; Abraham, A.; Snášel, V. Metaheuristic design of feedforward neural networks: A review of two decades of research. Eng. Appl. Artif. Intell. 2017, 60, 97–116. [Google Scholar] [CrossRef] [Green Version]
- Vazquez, R.A. Training spiking neural models using cuckoo search algorithm. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 679–686. [Google Scholar]
- Vazquez, R.A.; Garro, B.A. Training spiking neural models using artificial bee colony. Comput. Intell. Neurosci. 2015, 2015, 947098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enríquez-Gaytán, J.; Gómez-Castañeda, F.; Flores-Nava, L.; Moreno-Cadenas, J. Spiking neural network approaches PCA with metaheuristics. Electron. Lett. 2020, 56, 488–490. [Google Scholar] [CrossRef]
- Pavlidis, N.; Tasoulis, O.; Plagianakos, V.P.; Nikiforidis, G.; Vrahatis, M. Spiking neural network training using evolutionary algorithms. In Proceedings of the Proceedings, 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 4, pp. 2190–2194. [Google Scholar]
- Altamirano, J.S.; Ornelas, M.; Espinal, A.; Santiago-Montero, R.; Puga, H.; Carpio, J.M.; Tostado, S. Comparing Evolutionary Strategy Algorithms for Training Spiking Neural Networks. Res. Comput. Sci. 2015, 96, 9–17. [Google Scholar] [CrossRef]
- López-Vázquez, G.; Ornelas-Rodriguez, M.; Espinal, A.; Soria-Alcaraz, J.A.; Rojas-Domínguez, A.; Puga-Soberanes, H.; Carpio, J.M.; Rostro-Gonzalez, H. Evolutionary spiking neural networks for solving supervised classification problems. Comput. Intell. Neurosci. 2019, 2019, 4182639. [Google Scholar] [CrossRef]
- Liu, C.; Shen, W.; Zhang, L.; Du, Y.; Yuan, Z. Spike Neural Network Learning Algorithm Based on an Evolutionary Membrane Algorithm. IEEE Access 2021, 9, 17071–17082. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Ji, S.; Wuang, Z.; Wei, Y. Principal Component Analysis and Autoencoders. Available online: http://people.tamu.edu/~sji/classes/PCA.pdf (accessed on 22 April 2021).
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Asghari, P.; Rahmani, A.M.; Javadi, H.H.S. Internet of Things applications: A systematic review. Comput. Netw. 2019, 148, 241–261. [Google Scholar] [CrossRef]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Al-Garadi, M.A.; Mohamed, A.; Al-Ali, A.K.; Du, X.; Ali, I.; Guizani, M. A survey of machine and deep learning methods for internet of things (IoT) security. IEEE Commun. Surv. Tutor. 2020, 22, 1646–1685. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Chen, X.; Li, E.; Zeng, L.; Luo, K.; Zhang, J. Edge intelligence: Paving the last mile of artificial intelligence with edge computing. Proc. IEEE 2019, 107, 1738–1762. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2015; Volume 25. [Google Scholar]
- Erhan, D.; Courville, A.; Bengio, Y.; Vincent, P. Why does unsupervised pre-training help deep learning? In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 201–208. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Bennis, F.; Bhattacharjya, R.K. Nature-inspired Methods for Metaheuristics Optimization: Algorithms and Applications in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2020; Volume 16. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Izhikevich, E.M. Dynamical Systems in Neuroscience; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Handwritten Digits Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/Pen-Based+Recognition+of+Handwritten+Digits (accessed on 29 April 2021).
- Flowers, Fruits and Faces Data Set. Available online: https://es.dreamstime.com/foto-de-archivo-sistema-de-caras-de-la-gente-image79273852 (accessed on 22 April 2021).
- Fused Optical-Radar Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/Crop+mapping+using+fused+optical-radar+data+set# (accessed on 29 April 2021).
- Lee, J.A.; Verleysen, M. Quality assessment of dimensionality reduction: Rank-based criteria. Neurocomputing 2009, 72, 1431–1443. [Google Scholar] [CrossRef]
- Lueks, W.; Mokbel, B.; Biehl, M.; Hammer, B. How to evaluate dimensionality reduction?—Improving the co-ranking matrix. arXiv 2011, arXiv:1110.3917. [Google Scholar]
- Xu, Y.; Tang, H.; Xing, J.; Li, H. Spike trains encoding and threshold rescaling method for deep spiking neural networks. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–6. [Google Scholar]
- Mostafa, H. Supervised learning based on temporal coding in spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3227–3235. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Srinivasan, G.; Panda, P.; Roy, K. Deep spiking convolutional neural network trained with unsupervised spike-timing-dependent plasticity. IEEE Trans. Cogn. Dev. Syst. 2018, 11, 384–394. [Google Scholar]
- Zhang, T.; Jia, S.; Cheng, X.; Xu, B. Tuning Convolutional Spiking Neural Network With Biologically Plausible Reward Propagation. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
















| Variables and Parameters | Name |
|---|---|
| v | membrane potential |
| u | membrane recovery |
| resting membrane potential | |
| cutoff or threshold potential | |
| C | membrane capacitance |
| I | injected current |
| dynamics type parameters |
| Neural Model Configurations (Acronym) | a | b | c | d |
|---|---|---|---|---|
| Regular Spiking (RS) | 8 | |||
| Fast Spiking (FS) | 2 | |||
| Low-Threshold Spiking (LTS) | 2 | |||
| Chattering (CH) | 2 | |||
| Intrinsically Bursting (IB) | 4 |
| Name | Value |
|---|---|
| a | ms |
| b | |
| c | mV |
| d | mV |
| k | 0.9 |
| C | 100 pF |
| mV | |
| mV | |
| 35 mV |
| Name | Data | Features | Classes | Dimension |
|---|---|---|---|---|
| Handwriting Numbers | 1000 | 16 | 10 | |
| Fruits, Flowers, and Faces | 300 | 67 | 3 | |
| Croplands | 700 | 174 | 7 |
| Parameters |
|---|
| N, number of samples in one class. |
| {}, set of distances between the center of the cluster and all N samples; |
| by a landmark experiment, in the same class. |
| {}, set of distances between the center of the cluster and all N samples; |
| by the spiking network, in the same class. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anzueto-Ríos, Á.; Gómez-Castañeda, F.; Flores-Nava, L.M.; Moreno-Cadenas, J.A. Approaching Optimal Nonlinear Dimensionality Reduction by a Spiking Neural Network. Electronics 2021, 10, 1679. https://doi.org/10.3390/electronics10141679
Anzueto-Ríos Á, Gómez-Castañeda F, Flores-Nava LM, Moreno-Cadenas JA. Approaching Optimal Nonlinear Dimensionality Reduction by a Spiking Neural Network. Electronics. 2021; 10(14):1679. https://doi.org/10.3390/electronics10141679
Chicago/Turabian StyleAnzueto-Ríos, Álvaro, Felipe Gómez-Castañeda, Luis M. Flores-Nava, and José A. Moreno-Cadenas. 2021. "Approaching Optimal Nonlinear Dimensionality Reduction by a Spiking Neural Network" Electronics 10, no. 14: 1679. https://doi.org/10.3390/electronics10141679
APA StyleAnzueto-Ríos, Á., Gómez-Castañeda, F., Flores-Nava, L. M., & Moreno-Cadenas, J. A. (2021). Approaching Optimal Nonlinear Dimensionality Reduction by a Spiking Neural Network. Electronics, 10(14), 1679. https://doi.org/10.3390/electronics10141679