Estimating the Memory Consumption of a Hardware IP Defragmentation Block
Abstract
:1. Introduction
1.1. Significance of the Research
- 5G infrastructure, e.g., packet data gateways;
- Security appliances, such as firewall or Intrusion Detection System (IDS).
1.2. Problem Statement
1.3. Contribution of the Article
- carrying out an extensive design space exploration that yields robust confidence intervals for obtained performance metrics and confirms the original hypothesis about the performance of an IP reassembly block
- developing an original Monte Carlo validation method for estimating the performance of network protocol accelerators and, in particular, for an IP reassembly block.
1.4. Paper Organization
2. Related Work
2.1. Ip Defragmentation
2.1.1. References
2.1.2. Ip Defragmentation Algorithm
- id—a 16-bit field identifying the fragment series;
- total length—length of the entire IP datagram;
- offset—a 16-bit data offset from the beginning of the original (not fragmented) IP packet;
- MF—“more fragments” flag indicating that this is not the last fragment;
- DF—“do not fragment” flag preventing fragmentation by gateways and routers;
- proto—type of the payload, e.g., TCP or UDP.
- id—a 32-bit field identifying the fragment series;
- payload length—length of the payload (including extension headers);
- offset—a 16-bit data offset from the beginning of the original (not fragmented) IP packet;
- M—“more fragments” flag indicating that this is not the last fragment;
- next—type of the next header: e.g.,: TCP or UDP or an extension header.
- —for IPv4
- —for IPv6.
2.2. Network Traffic Statistics
2.3. Flow State Memory and Caching
2.4. Creating Synthetic Traffic in Networking
2.5. Summary of the Related Works
3. Materials and Methods
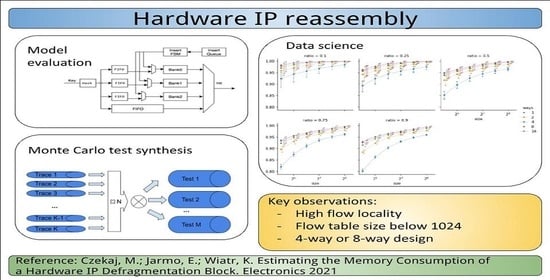
3.1. Software Simulation of the Ip Reassembly Module
3.1.1. Flow Table Design
- Constant associativity A, which is a design parameter;
- Constant number of flow table entries , where B is a number of buckets or “sets” (also a design parameter);
- Least Recently Used (LRU) replacement policy based on a timestamp (e.g., a cycle or a packet counter).
- Finite flow table with a predefined size in the range from 16 to 512 entries.
- Fixed associativity A from 1 to 16
- Infinite packet buffer space. Payload buffering limitations are not simulated.
- Constant 40-byte flow key constructed from .
- LRU replacement policy based on a timestamp.
- IP Fragments are properly defragmented even when they arrive out of order or duplicated.
- Infinite fragment list.
- No data flow modeling.
- No cycle-level modeling.
3.1.2. Simulation System
3.2. Performance Estimation Methodology
3.2.1. Rationale
3.2.2. Test Generation
- Abnormal network events captured in sampled traffic;
- Time-dependent traffic characteristics (network traffic from a single time zone follows daily and weekly patterns [26]);
- Insufficient bandwidth in the original sampled traffic;
- Operator-specific traffic profile.
- —a set of all packet traces, each trace spans equal time;
- —a packet trace, i.e., a sequence of packets each with the associated timestamp , such that a first timestamp is 0 (the trace records only the relative time);
- M—the desired total number of tests;
- N—the number of packet traces forming a single test, ;
- —predefined IPv4 address constants.
3.2.3. Estimators and Confidence Intervals
4. Results
4.1. Data Sources
4.2. Simulation Parameters
- The total number of traces is with each trace lasting 15 min
- −
- 130 packet traces from MAWI;
- −
- 93 traces from WAND with 30 min length were split into two halves, giving 186 traces, each lasting 15 min.
- The total number of individual tests was chosen as .
- Each individual test was a mix of , where R is a test composition ratio
- For each test run, the simulation program tested the following flow table parameters (see Figure 4):
- −
- The number of flow table entries is ;
- −
- The associativity (number of ways) .
- The bandwidth of a synthetic packet trace (mixed by Algorithm 3) increases with the ratio R. This is important in the case of IP fragmentation, as the original packet traces contain less than 1% of the relevant traffic.
- The statistical diversity (variance of the estimators) obtained from samples diminish as the R grows. This is observed empirically in Section 4.3 and can be deduced from the standard formula of a variance of a sample mean:
| Algorithm 1 Test generation. |
Require:S, M, N
|
| Algorithm 2 Trace anonymization |
function Anonymize()
|
| Algorithm 3 Trace mixing. |
function Mix(S)
|
4.3. Simulation Results
4.3.1. Efficiency
4.3.2. Intra-Arrival
4.3.3. Flow Parallelism
4.3.4. Flow Length
5. Discussion
5.1. Simulation Results
5.2. Methodology
5.3. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronyms
| CAM | Content-Addressable Memory |
| CDF | Cumulative Distribution Function |
| CI | Confidence Interval |
| CI | Confidence Interval |
| DPI | Deep Packet Inspection |
| FPGA | Field Programmable Gate Array |
| IDS | Intrusion Detection System |
| ISP | Internet Service Provider |
| LRU | Least Recently Used |
| MTU | Maximum Transmission Unit |
| NIC | Network Interface Card |
| SDN | Software-Defined Networking |
| SOC | System On Chip |
| SRAM | Synchronous Random Access Memory |
| TCAM | Ternary Content-Addressable Memory |
| TLS | Transport Layer Security |
Glossary
| MPLS/GRE | A tunnel protocol based on Multi Protocol Label Switching (MPLS) and Greneric Routing Encapsulation(GRE) |
| HBM2 | High Bandwidth Memory, an on-chip dynamic RAM optimized for high bandwidth. Puplar in Graphics Prosessing Units (GPUs) and high-end FPGAs |
| DDOS | Distributed Denial of Service attack, a massive request stream aimed at overwhelming the network service originated from many (geographically distributed) clients |
Appendix A. Estimation Method
References
- Shannon, C.; Moore, D.; Claffy, K.C. Beyond folklore: Observations on fragmented traffic. IEEE/Acm Trans. Netw. 2002, 10, 709–720. [Google Scholar] [CrossRef]
- Rescorla, E. The Transport Layer Security (TLS) Protocol Version 1.3; 2018; Available online: https://datatracker.ietf.org/doc/html/rfc8446 (accessed on 8 April 2021).
- Kent, S.; Seo, K. Security Architecture for the Internet Protocol; RFC 4301; 2005; Available online: http://www.rfc-editor.org/rfc/rfc4301.txt (accessed on 8 April 2021).
- Worster, T.; Rekhter, Y.; Rosen, E. Encapsulating MPLS in IP or Generic Routing Encapsulation (GRE); RFC 4023; 2005; Available online: https://www.rfc-editor.org/rfc/rfc4023.html (accessed on 8 April 2021).
- Mahalingam, M.; Dutt, D.; Duda, K.; Agarwal, P.; Kreeger, L.; Sridhar, T.; Bursell, M.; Wright, C. Virtual eXtensible Local Area Network (VXLAN): A Framework for Overlaying Virtualized Layer 2 Networks over Layer 3 Networks; RFC 7348; 2014; Available online: http://www.rfc-editor.org/rfc/rfc7348.txt (accessed on 8 April 2021).
- Holz, R.; Hiller, J.; Amann, J.; Razaghpanah, A.; Jost, T.; Vallina-Rodriguez, N.; Hohlfeld, O. Tracking the deployment of TLS 1.3 on the Web: A story of experimentation and centralization. ACM Sigcomm Comput. Commun. Rev. 2020, 50, 3–15. [Google Scholar] [CrossRef]
- Kunz, A.; Salkintzis, A. Non-3GPP Access Security in 5G. J. ICT Stand. 2020, 8, 41–56. [Google Scholar] [CrossRef]
- Bonica, R.; Baker, F.; Huston, G.; Hinden, B.; Troan, O.; Gont, F. IP Fragmentation Considered Fragile; Technical Report, IETF Internet-Draft (Draft-Ietf-Intarea-Frag-Fragile), Work in Progress…; 2019; Available online: https://datatracker.ietf.org/doc/rfc8900/ (accessed on 8 April 2021).
- Intel. Intel® FPGA Programmable Acceleration Card N3000 for Networking. 2016. Available online: https://www.intel.com/content/dam/www/programmable/us/en/pdfs/literature/po/intel-fpga-programmable-acceleration-card-n3000-for-networking.pdf (accessed on 8 April 2021).
- NVidia. ConnectX-6 DxDual-Port 100GbE/Single-Port 200GbE SmartNIC. 2021. Available online: https://www.mellanox.com/products/ethernet-adapters/connectx-6-dx (accessed on 8 April 2021).
- Intel. Intel® XL710 40 GbE Ethernet Adapter. 2016. Available online: https://i.dell.com/sites/csdocuments/Shared-Content_data-Sheets_Documents/en/us/Intel_Dell_X710_Product_Brief_XL710_40_GbE_Ethernet_Adapter.pdf (accessed on 8 April 2021).
- Marvell. Marvell® Infrastructure Processors. 2021. Available online: https://www.marvell.com/products/infrastructure-processors.html (accessed on 8 April 2021).
- Xilinx. Xilinx Alveo Adaptable Accelerator Cards for Data Center Workloads. 2021. Available online: https://www.xilinx.com/products/boards-and-kits/alveo.html (accessed on 8 April 2021).
- Yamaki, H. Effective cache replacement policy for packet processing cache. Int. J. Commun. Syst. 2020, 33, e4526. [Google Scholar] [CrossRef]
- Tanaka, K.; Yamaki, H.; Miwa, S.; Honda, H. Evaluating architecture-level optimization in packet processing caches. Comput. Networks 2020, 181, 107550. [Google Scholar] [CrossRef]
- Congdon, P.T.; Mohapatra, P.; Farrens, M.; Akella, V. Simultaneously reducing latency and power consumption in openflow switches. IEEE/ACM Trans. Netw. (TON) 2014, 22, 1007–1020. [Google Scholar] [CrossRef]
- Postel, J. Internet Protocol; STD 5; 1981; Available online: http://www.rfc-editor.org/rfc/rfc791.txt (accessed on 8 April 2021).
- Touch, J. Updated Specification of the IPv4 ID Field; RFC 6864; 2013; Available online: http://www.rfc-editor.org/rfc/rfc6864.txt (accessed on 8 April 2021).
- Deering, S.; Hinden, R. Internet Protocol, Version 6 (IPv6) Specification; STD 86; 2017; Available online: https://www.omgwiki.org/dido/doku.php?id=dido:public:ra:xapend:xapend.b_stds:tech:ietf:ipv6 (accessed on 8 April 2021).
- NXP. Overview of Autonomous IPSec with QorIQT Series Processors. 2014. Available online: https://www.nxp.com/files-static/training/doc/ftf/2014/FTF-NET-F0111.pdf (accessed on 8 April 2021).
- Lin, V.; Manral, V. Methods and Systems for Fragmentation and Reassembly for IP Tunnels in Hardware Pipelines. U.S. Patent App. 11/379,559, 23 April 2006. [Google Scholar]
- Zhao, Y.; Yuan, R.; Wang, W.; Meng, D.; Zhang, S.; Li, J. A Hardware-Based TCP Stream State Tracking and Reassembly Solution for 10G Backbone Traffic. In Proceedings of the 2012 IEEE Seventh International Conference on Networking, Architecture, and Storage, Xiamen, China, 28–30 June 2012; pp. 154–163. [Google Scholar]
- Ruiz, M.; Sidler, D.; Sutter, G.; Alonso, G.; López-Buedo, S. Limago: An FPGA-Based Open-Source 100 GbE TCP/IP Stack. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 9–13 September 2019; pp. 286–292. [Google Scholar] [CrossRef]
- Adamic, L.; Huberman, B. Zipfs law and the internet. Glottometrics 2002, 3, 143–150. [Google Scholar]
- Ribeiro, V.J.; Zhang, Z.L.; Moon, S.; Diot, C. Small-time scaling behavior of Internet backbone traffic. Comput. Netw. 2005, 48, 315–334. [Google Scholar] [CrossRef] [Green Version]
- Benson, T.; Akella, A.; Maltz, D.A. Network Traffic Characteristics of Data Centers in the Wild. In Proceedings of the IMC ’10: 10th ACM SIGCOMM Conference on Internet Measurement, Melbourne, Australia, 1–30 November 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 267–280. [Google Scholar] [CrossRef]
- Arfeen, M.A.; Pawlikowski, K.; Willig, A.; Mcnickle, D. Internet traffic modelling: From superposition to scaling. IET Netw. 2014, 3, 30–40. [Google Scholar] [CrossRef]
- Feldmeier, D.C. Improving Gateway Performance with a Routing-Table Cache. In Proceedings of the IEEE INFOCOM’88, Seventh Annual Joint Conference of the IEEE Computer and Communcations Societies, Networks: Evolution or Revolution? New Orleans, LA, USA, 27–31 March 1988; pp. 298–307. [Google Scholar]
- Kim, N.; Jean, S.; Kim, J.; Yoon, H. Cache replacement schemes for data-driven label switching networks. In Proceedings of the 2001 IEEE Workshop on High Performance Switching and Routing (IEEE Cat. No.01TH8552), Dallas, TX, USA, 29–31 May 2001; pp. 223–227. [Google Scholar] [CrossRef]
- Pfaff, B.; Pettit, J.; Koponen, T.; Jackson, E.; Zhou, A.; Rajahalme, J.; Gross, J.; Wang, A.; Stringer, J.; Shelar, P.; et al. The Design and Implementation of Open vSwitch. In Proceedings of the 12th USENIX Symposium on Networked Systems Design and Implementation (NSDI 15), Oakland, CA, USA, 4–6 May 2015; USENIX Association: Oakland, CA, USA, 2015; pp. 117–130. [Google Scholar]
- Okuno, M.; Nishimura, S.; Ishida, S.I.; Nishi, H. Cache-based network processor architecture: Evaluation with real network traffic. IEICE Trans. Electron. 2006, 89, 1620–1628. [Google Scholar] [CrossRef]
- Czekaj, M.; Jamro, E. Flow caching effectiveness in packet forwarding applications. Comput. Sci. 2019, 20. [Google Scholar] [CrossRef]
- Li, J.; Sun, Z.; Yan, J.; Yang, X.; Jiang, Y.; Quan, W. DrawerPipe: A Reconfigurable Pipeline for Network Processing on FPGA-Based SmartNIC. Electronics 2020, 9, 59. [Google Scholar] [CrossRef] [Green Version]
- Technologies, K. Network Visibility and Network Test Products. 2021. Available online: https://www.keysight.com/zz/en/cmp/2020/network-visibility-network-test.html (accessed on 8 April 2021).
- Spirent. High-Speed Ethernet Testing Solutions. 2021. Available online: https://www.spirent.com/solutions/high-speed-ethernet-testing (accessed on 8 April 2021).
- Erlacher, F.; Dressler, F. Testing ids using genesids: Realistic mixed traffic generation for ids evaluation. In Proceedings of the ACM SIGCOMM 2018 Conference on Posters and Demos, Budapest, Hungary, 20–25 August 2018; pp. 153–155. [Google Scholar]
- Cisco. TRex Realistic Traffic Generator. Available online: https://trex-tgn.cisco.com/ (accessed on 8 April 2021).
- Gadelrab, M.; Abou El Kalam, A.; Deswarte, Y. Manipulation of network traffic traces for security evaluation. In Proceedings of the 2009 International Conference on Advanced Information Networking and Applications Workshops, Bradford, UK, 26–29 May 2009; pp. 1124–1129. [Google Scholar]
- Cerqueira, V.; Torgo, L.; Mozetič, I. Evaluating time series forecasting models: An empirical study on performance estimation methods. Mach. Learn. 2020, 109, 1997–2028. [Google Scholar] [CrossRef]
- Sudarshan, T.; Mir, R.A.; Vijayalakshmi, S. Highly efficient LRU implementations for high associativity cache memory. In Proceedings of the 12 International Conference on Advances in Computing and Communications, ADCOM-2004, Ahmedabad, India, 15–18 December 2004; pp. 24–35. [Google Scholar]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Cambridge University Press: Cambridge, UK, 2016; Volume 5. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Young, G. 15. The Jackknife and Bootstrap. J. R. Stat. Soc. Ser. A (Stat. Soc.) 1996, 159, 631–632. [Google Scholar] [CrossRef]
- WITS: Waikato INTERNET Traffic Storage. 2013. Available online: https://wand.net.nz/wits/ (accessed on 8 April 2021).
- Cleary, J.; Graham, I.; McGregor, T.; Pearson, M.; Ziedins, L.; Curtis, J.; Donnelly, S.; Martens, J.; Martin, S. High precision traffic measurement. IEEE Commun. Mag. 2002, 40, 167–173. [Google Scholar] [CrossRef]
- WIDE Project. 2020. Available online: http://mawi.wide.ad.jp/mawi/ (accessed on 8 April 2021).
- Sony, C.; Cho, K. Traffic data repository at the WIDE project. In Proceedings of the USENIX 2000 Annual Technical Conference: FREENIX Track, San Diego, CA, USA, 18–23 June 2000; pp. 263–270. [Google Scholar]
- Politis, D.N.; Romano, J.P. Large sample confidence regions based on subsamples under minimal assumptions. Ann. Stat. 1994, 22, 2031–2050. [Google Scholar] [CrossRef]










| Problem | Length | Bandwidth | Connection State | Buffering |
|---|---|---|---|---|
| Connection tracking | short and long | high | optional | no |
| IP defragmentation | short | low | mandatory | yes |
| TCP reassembly | short | high | mandatory | yes |
| Publication | Protocol | Test Data | Ways | Size |
|---|---|---|---|---|
| Yamaki [14] | TCP, UDP | samples | 4, 8 | 1 K |
| Tanaka [15] | TCP, UDP | samples | 2, 4 | 128–128 K |
| Congdon [16] | TCP, UDP | samples | full | 2–64 |
| This work | IPv4,IPv6 | mixing samples | 1, 2, 4, 8 | 16–512 |
| Ratio | High Slope | Low Slope | Mean Slope | Min. |
|---|---|---|---|---|
| 0.10 | 0.46589 | 0.30953 | 0.40379 | 0.97732 |
| 0.25 | 0.46042 | 0.39083 | 0.42903 | 0.98409 |
| 0.50 | 0.46382 | 0.41744 | 0.44497 | 0.98323 |
| 0.75 | 0.46755 | 0.44189 | 0.45782 | 0.97932 |
| 0.90 | 0.46907 | 0.45781 | 0.46386 | 0.97625 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czekaj, M.; Jamro, E.; Wiatr, K. Estimating the Memory Consumption of a Hardware IP Defragmentation Block. Electronics 2021, 10, 2015. https://doi.org/10.3390/electronics10162015
Czekaj M, Jamro E, Wiatr K. Estimating the Memory Consumption of a Hardware IP Defragmentation Block. Electronics. 2021; 10(16):2015. https://doi.org/10.3390/electronics10162015
Chicago/Turabian StyleCzekaj, Maciej, Ernest Jamro, and Kazimierz Wiatr. 2021. "Estimating the Memory Consumption of a Hardware IP Defragmentation Block" Electronics 10, no. 16: 2015. https://doi.org/10.3390/electronics10162015
APA StyleCzekaj, M., Jamro, E., & Wiatr, K. (2021). Estimating the Memory Consumption of a Hardware IP Defragmentation Block. Electronics, 10(16), 2015. https://doi.org/10.3390/electronics10162015