Evolutionary Coalitional Game-Based Cooperative Localization in Vehicular Networks
Abstract
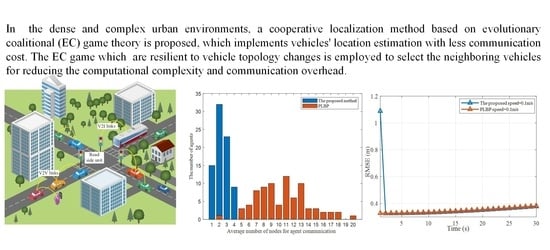
:1. Introduction
2. Materials and Methods
2.1. Network Model
2.2. Belief Propagation Algorithm for Cooperative Localization
| Algorithm 1: Belief propagation of cooperative localization |
| Initialization: |
| nodesin parallel |
| The vehicle discovers its neighboring vehicles and RSUs. |
| The vehicle measures the distance between it and its neighbors. |
| For . |
| The vehicle broadcasts the belief . |
| The vehicle receives from the neighbors. |
| Vehicle calculates the incoming and outgoing message. |
| Vehicle calculates the new belief . |
| end for |
| end parallel |
2.3. Evolutionary Coalitional Game Algorithm Based Cooperative Localizaion
- Players: The finite vehicles join in the game of cooperative localization. The RSUs assist in vehicle localization but do not play a role in games.
- Population: All vehicles form coalitions, and each coalition belongs to a population.
- Strategy: The vehicle’s strategy set is defined in the neighboring coalitions, and the vehicle determines its activities based on the actions of other vehicles.
- Payoff: The vehicle’s payoff is influenced by its connected neighbor vehicles. Each vehicle determines which coalition to join according to the preference profile set during the formation and strategy learning stage.
| Algorithm 2: Evolutionary coalitional game based cooperative localization |
| Initialization: The vehicle discovers its neighboring vehicles. |
| For Time |
| Range measurement is implemented, where . |
| The RSUs broadcast their beliefs (positions). Vehicle forms initial coalitions by calculating and exchanging with neighboring vehicles. |
| Vehicle calculates for neighboring vehicles. |
| Vehicle determines to join in or to quit the coalition according to . |
| For Iteration |
| The message is calculated and transmitted from neighboring vehicle to vehicle , where the vehicle belongs to the same coalition with the vehicle . |
| The vehicle broadcasts its belief (the location estimation ). |
| Until Iteration |
| Until Time |
3. Results
- (1)
- Localization performance
- (2)
- Complexity and Network Traffic
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bounini, F.; Gingras, D.; Pollart, H.; Gruyer, D. From Simultaneous Localization and Mapping to Collaborative Localization for Intelligent Vehicles. IEEE Intell. Transp. Syst. Mag. 2021, 13, 196–216. [Google Scholar] [CrossRef]
- Cao, Z.; Yang, D.; Jiang, K.; Xu, S. Monocular Connected-Vehicle Position Estimation on Sloping and Uneven Roads. IEEE Intell. Transp. Syst. Mag. 2022, 14, 228–241. [Google Scholar] [CrossRef]
- Liu, D.; Cui, Y.; Guo, X.; Ding, W.; Yang, B.; Chen, Y. Visual Localization for Autonomous Driving: Mapping the Accurate Location in the City Maze. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 3170–3177. [Google Scholar]
- Yuan, W.; Liu, F.; Masouros, C.; Yuan, J.; Ng, D.W.K.; Gonzalez-Prelcic, N. Bayesian Predictive Beamforming for Vehicular Networks: A Low-Overhead Joint Radar-Communication Approach. IEEE Trans. Wireless Commun. 2021, 20, 1442–1456. [Google Scholar] [CrossRef]
- Kassas, Z.Z.M.; Maaref, M.; Morales, J.J.; Khalife, J.J.; Shamei, K. Robust Vehicular Localization and Map Matching in Urban Environments Through IMU, GNSS, and Cellular Signals. IEEE Intell. Transp. Sys. Mag. 2020, 12, 36–52. [Google Scholar] [CrossRef]
- Eskandarian, A.; Wu, C.; Sun, C. Research Advances and Challenges of Autonomous and Connected Ground Vehicles. IEEE Trans. Intell. Transp. Sys. 2021, 22, 683–711. [Google Scholar] [CrossRef]
- Wymeersch, H.; Seco-Granados, G.; Destino, G.; Dardari, D.; Tufvesson, F. 5G mmWave Positioning for Vehicular Networks. IEEE Wirel. Commun. 2017, 24, 80–86. [Google Scholar] [CrossRef] [Green Version]
- 3GPP TS38.305; NG Radio Access Network (NG-RAN); User Equipment (UE) Positioning in NG-RAN. 3GPP: Sophia Antipolis, France, 2019.
- Kim, H.; Granstrom, K.; Gao, L.; Battistelli, G.; Kim, S.; Wymeersch, H. 5G mmWave Cooperative Positioning and Mapping Using Multi-Model PHD Filter and Map Fusion. IEEE Trans. Wireless Commun. 2020, 19, 3782–3795. [Google Scholar] [CrossRef] [Green Version]
- Luo, F.; Wang, S.; Gong, Y.; Jing, X.; Zhang, L. Geographical Information Enhanced Cooperative Localization in Vehicular Ad-Hoc Networks. IEEE Signal Process. Lett. 2018, 25, 556–560. [Google Scholar] [CrossRef]
- Meng, W.; Chu, X.; Lu, Z.; Wang, L.; Wen, X.; Li, M. V2V Communication Assisted Cooperative Localization for Connected Vehicles. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Wymeersch, H.; Lien, J.; Win, M.Z. Cooperative Localization in Wireless Networks. Proc. IEEE 2009, 97, 427–450. [Google Scholar] [CrossRef]
- Ihler, A.; Fisher, J.; Moses, R.; Willsky, A. Nonparametric belief propagation for self-localization of sensor networks. IEEE J. Sel. Areas Commun. 2005, 23, 809–819. [Google Scholar] [CrossRef] [Green Version]
- García-Fernández, Á.F.; Svensson, L.; Särkkä, S. Cooperative Localization Using Posterior Linearization Belief Propagation. IEEE Trans. Veh. Technol. 2018, 67, 832–836. [Google Scholar] [CrossRef]
- Tang, C.; Dou, L. An Improved Game Theory-Based Cooperative Localization Algorithm for Eliminating the Conflicting Information of Multi-Sensors. Sensors 2020, 20, 5579. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Zhang, R.; Cheng, X.; Yang, L.; Jiao, B. Network formation games for the link selection of cooperative localization in wireless networks. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014; pp. 4577–4582. [Google Scholar]
- Hedhly, K.; Laaraiedh, M.; AbdelKefi, F.; Siala, M. Optimizing communication costs based on novel cooperative localization techniques using coalitional game theory in wireless networks. In Proceedings of the 2018 14th International Wireless Communications & Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018; pp. 1043–1046. [Google Scholar]
- Zhang, R.; Zhao, Z.; Cheng, X.; Yang, L. Overlapping Coalition Formation Game Based Opportunistic Cooperative Localization Scheme for Wireless Networks. IEEE Trans. Commun. 2017, 65, 3629–3642. [Google Scholar]
- Tian, K.M.; Tong, S.; Zhang, K. An EKF based overlapping coalition formation game for cooperative wireless network navigation. IET Commun. 2021, 15, 2407–2424. [Google Scholar]
- Abu-Shaban, Z.; Wymeersch, H.; Abhayapala, T.; Seco-Granados, G. Distributed Two-Way Localization Bounds for 5G mmWave Systems. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Khan, M.A.; Tembine, H.; Vasilakos, A.V. Evolutionary coalitional games: Design and challenges in wireless networks. IEEE Wireless Commun. 2012, 19, 50–56. [Google Scholar] [CrossRef]
- Asheralieva, A.; Quek, T.Q.S.; Niyato, D. An Asymmetric Evolutionary Bayesian Coalition Formation Game for Distributed Resource Sharing in a Multi-Cell Device-to-Device Enabled Cellular Network. IEEE Trans. Wireless Commun. 2018, 17, 3752–3767. [Google Scholar] [CrossRef]
- Shen, Y.; Wymeersch, H.; Win, M.Z. Fundamental Limits of Wideband Localization—Part II: Cooperative Networks. IEEE Trans. Inform. Theory 2010, 56, 4981–5000. [Google Scholar] [CrossRef] [Green Version]
- Mazuelas, S.; Shen, Y.; Win, M.Z. Spatiotemporal information coupling in network navigation. IEEE Trans. Inform. Theory 2018, 64, 7759–7779. [Google Scholar] [CrossRef]
- Xiong, Y.; Wu, N.; Shen, Y.; Win, M.Z. Cooperative localization in massive networks. IEEE Trans. Inform. Theory 2021, 68, 1–23. [Google Scholar] [CrossRef]
- Luo, X.; Tembine, H. Evolutionary coalitional games for random access control. In Proceedings of the 2013 Proceedings IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 535–539. [Google Scholar]
- Yuan, W.; Wu, N.; Guo, Q.; Huang, X.; Li, Y.; Hanzo, L. TOA-Based Passive Localization Constructed Over Factor Graphs: A Unified Framework. IEEE Trans. Commun. 2019, 67, 6952–6965. [Google Scholar] [CrossRef] [Green Version]
- 3GPP TS 36.331; Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA) and Evolved Universal Terrestrial Radio Access Network (E-UTRAN). 3GPP: Sophia Antipolis, France, 2017.
- Xiong, Y.; Wu, N.; Shen, Y.; Win, M.Z. Cooperative Network Synchronization: Asymptotic Analysis. IEEE Trans. Signal Process. 2018, 66, 757–772. [Google Scholar] [CrossRef]
- Yuan, W.; Wu, N.; Etzlinger, B.; Wang, H.; Kuang, J. Cooperative Joint Localization and Clock Synchronization Based on Gaussian Message Passing in Asynchronous Wireless Networks. IEEE Trans. Veh. Technol. 2016, 65, 7258–7273. [Google Scholar] [CrossRef] [Green Version]
- Etzlinger, B.; Meyer, F.; Hlawatsch, F.; Springer, A.; Wymeersch, H. Cooperative Simultaneous Localization and Synchronization in Mobile Agent Networks. IEEE Trans. Signal Process. 2017, 65, 3587–3602. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Yuan, J.; Kwan Ng, D.W. Parametric Message-Passing for Joint Localization and Synchronization in Cooperative Networks. In Proceedings of the 2020 IEEE Global Communications Conference (GLOBECOM), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, T.; Zou, D.; Lu, X.; Bi, C. Evolutionary Coalitional Game-Based Cooperative Localization in Vehicular Networks. Electronics 2022, 11, 638. https://doi.org/10.3390/electronics11040638
Yin T, Zou D, Lu X, Bi C. Evolutionary Coalitional Game-Based Cooperative Localization in Vehicular Networks. Electronics. 2022; 11(4):638. https://doi.org/10.3390/electronics11040638
Chicago/Turabian StyleYin, Ting, Decai Zou, Xiaochun Lu, and Cheng Bi. 2022. "Evolutionary Coalitional Game-Based Cooperative Localization in Vehicular Networks" Electronics 11, no. 4: 638. https://doi.org/10.3390/electronics11040638
APA StyleYin, T., Zou, D., Lu, X., & Bi, C. (2022). Evolutionary Coalitional Game-Based Cooperative Localization in Vehicular Networks. Electronics, 11(4), 638. https://doi.org/10.3390/electronics11040638