Variability and Reliability of Single-Walled Carbon Nanotube Field Effect Transistors
Abstract
:1. Introduction

 (Figure 1a), aC-C = 0.142 nm is the C–C bond length, t ~ −3 eV is the C–C bonding energy. SWCNTs with n = m are called armchair nanotubes and always show metallic behavior, whereas SWCNTs with n ≠ m either show metallic behavior for mod (n − m)/3 = 0 or semiconducting behavior for mod (n − m)/3 = 1, 2. SWCNTs with m = 0 are called zigzag nanotubes and the rest with n ≠ m ≠ 0 are called chiral nanotubes.
(Figure 1a), aC-C = 0.142 nm is the C–C bond length, t ~ −3 eV is the C–C bonding energy. SWCNTs with n = m are called armchair nanotubes and always show metallic behavior, whereas SWCNTs with n ≠ m either show metallic behavior for mod (n − m)/3 = 0 or semiconducting behavior for mod (n − m)/3 = 1, 2. SWCNTs with m = 0 are called zigzag nanotubes and the rest with n ≠ m ≠ 0 are called chiral nanotubes.

2. Configurations and Performance of SWCNT-FET
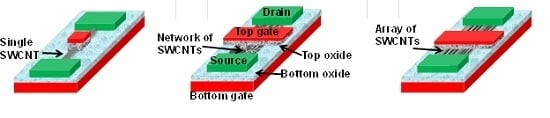
2.1. Device Geometry

2.2. Materials for SWCNT-FETs
2.3. FETs with Single SWCNT
2.4. FETs with Multiple SWCNTs



3. Variability in SWCNT-FETs
3.1. Variability in FETs with Single SWCNT

3.2. Variability in FETs with Multiple SWCNTs





4. Reliability of SWCNT-FETs
4.1. Interface Defects in SWCNT-FETs
4.2. Oxide Defects in SWCNT-FETs

4.3. Hysteresis in SWCNT-FETs


4.4. Low-Frequency Noise in SWCNT-FETs
| Reference | EOT [nm] | D [μm−1] | Ξ | Vg,max [V] | EP,max [MV cm−1] | Eox,max [MV cm−1] | Type of Dielectric |
|---|---|---|---|---|---|---|---|
| [9] Cao et al., Nature ʼ08 | 8.2 | ~6 | 0.01 | 2 | 2.44 | 0.02 | HfO2 |
| [106] Weitz et al., NL ʼ07 | 20.3 | 5.48 | 0.16 | 2 | 0.98 | 0.16 | Octadecyltrichlor osilanated-SiO2 |
| [107] Hur et al., JACS ʼ05 | 6.9 | 1 (Single CNT) | 0.01 | 1 | 1.45 | 0.02 | Octachlorotrisilox ane-capped organic dielectric |
| [83] Kim et al., NLʼ03 | 500 | 1 (Single CNT) | 0.36 | 10 | 0.2 | 0.07 | SiO2 with PMMA coating |
| [103] McGill et al., APL ʼ06 | 100 | ~3 | 0.30 | 2 | 0.2 | 0.06 | Octadecyltrichlor osilanated-SiO2 |
| [121] Hu et al., Phys. E ʼ08 | 200 | ~3 | 0.45 | 10 | 0.5 | 0.23 | Aminopropyltrieth oxysilaned-SiO2 |
| [131] Kim et al., APL ʼ07 | 6.5 | 1 (Single CNT) | 0.01 | 1 | 1.54 | 0.02 | Al2O3 |
| [94] Jin et al., AFM ʼ12 | 40 | ~6 | 0.29 | 6 | 1.5 | 0.45 | Spin-on-glass (SOG) + HfO2 |




4.5. Radiation Damage in SWCNT-FETs



4.6. Performance Degradation in SWCNT-FETs

5. Summary and Outlook
Acknowledgments
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Datta, S. Quantum Transport: Atom to Transistor, 2nd ed.; Cambridge University Press: Cambridge CB2 2RU, UK, 2005. [Google Scholar]
- Saito, R.; Sato, K.; Oyama, Y.; Jiang, J.; Samsonidze, G.G.; Dresselhaus, G.; Dresselhaus, M.S. Cutting lines near the Fermi energy of single-wall carbon nanotubes. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Jorio, A.; Pimenta, M.A.; Souza, A.G.; Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Characterizing carbon nanotube samples with resonance Raman scattering. New J. Phys. 2003, 5. [Google Scholar] [CrossRef]
- Zhou, X.J.; Park, J.Y.; Huang, S.M.; Liu, J.; McEuen, P.L. Band structure, phonon scattering, and the performance limit of single-walled carbon nanotube transistors. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Durkop, T.; Getty, S.A.; Cobas, E.; Fuhrer, M.S. Extraordinary mobility in semiconducting carbon nanotubes. Nano Lett. 2004, 4, 35–39. [Google Scholar] [CrossRef]
- Guo, J.; Goasguen, S.; Lundstrom, M.; Datta, S. Metal-insulator-semiconductor electrostatics of carbon nanotubes. Appl. Phys. Lett. 2002, 81, 1486–1488. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and mechanics for stretchable electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef]
- Cao, Q.; Kim, H.S.; Pimparkar, N.; Kulkarni, J.P.; Wang, C.J.; Shim, M.; Roy, K.; Alam, M.A.; Rogers, J.A. Medium-scale carbon nanotube thin-film integrated circuits on flexible plastic substrates. Nature 2008, 454, 495–500. [Google Scholar] [CrossRef]
- Sun, Y.; Rogers, J.A. Inorganic semiconductors for flexible electronics. Adv. Mater. 2007, 19, 897–1916. [Google Scholar]
- Perelaer, J.; Smith, P.J.; Mager, D.; Soltman, D.; Volkman, S.K.; Subramanian, V.; Korvink, J.G.; Schubert, U.S. Printed electronics: The challenges involved in printing devices, interconnects, and contacts based on inorganic materials. J. Mater.Chem. 2010, 20, 8446–8453. [Google Scholar] [CrossRef]
- Cao, Q.; Hur, S.H.; Zhu, Z.T.; Sun, Y.G.; Wang, C.J.; Meitl, M.A.; Shim, M.; Rogers, J.A. Highly bendable, transparent thin-film transistors that use carbon-nanotube-based conductors and semiconductors with elastomeric dielectrics. Adv. Mater. 2006, 18, 304–309. [Google Scholar] [CrossRef]
- Xiong, F.; Liao, A.D.; Estrada, D.; Pop, E. Low-power switching of phase-change materials with carbon nanotube electrodes. Science 2011, 332, 568–570. [Google Scholar] [CrossRef]
- Kianian, S.; Rosendale, G.; Manning, M.; Hamilton, D.; Huang, X.M.H.; Robinson, K.; Kim, Y.W.; Rueckes, T. A 3D stackable Carbon Nanotube-based nonvolatile memory (NRAM). In Proceedings of the ESSDERC, Sevilla, Spain, 14–16 September, 2010; pp. 404–407.
- Rosendale, G.; Kianian, S.; Manning, M.; Hamilton, D.; Huang, X.M.H.; Robinson, K.; Kim, Y.W.; Rueckes, T. A 4 Megabit Carbon Nanotube-based nonvolatile memory (NRAM). In Proceedings of the ESSDERC, Sevilla, Spain, 14–16 September, 2010; pp. 478–481.
- Fuhrer, M.S.; Kim, B.M.; Durkop, T.; Brintlinger, T. High-mobility nanotube transistor memory. Nano Lett. 2002, 2, 755–759. [Google Scholar] [CrossRef]
- Di Bartolomeo, A.; Yang, Y.; Rinzan, M.B.M.; Boyd, A.K.; Barbara, P. Record endurance for single-walled carbon nanotube-based memory cell. Nanoscale Res. Lett. 2010, 5, 1852–1855. [Google Scholar] [CrossRef]
- Jarosz, P.R.; Shaukat, A.; Schauerman, C.M.; Cress, C.D.; Kladitis, P.E.; Ridgley, R.D.; Landi, B.J. High-performance, lightweight coaxial cable from carbon nanotube conductors. ACS Appl. Mater. Interfaces 2012, 4, 1103–1109. [Google Scholar] [CrossRef]
- Nair, P.R.; Alam, M.A. Performance limits of nanobiosensors. Appl. Phys. Lett. 2006, 88, 233120:1–233120:3. [Google Scholar]
- Pengfei, Q.F.; Vermesh, O.; Grecu, M.; Javey, A.; Wang, O.; Dai, H.J.; Peng, S.; Cho, K.J. Toward large arrays of multiplex functionalized carbon nanotube sensors for highly sensitive and selective molecular detection. Nano Lett. 2003, 3, 347–351. [Google Scholar] [CrossRef]
- Collins, P.G.; Bradley, K.; Ishigami, M.; Zettl, A. Extreme oxygen sensitivity of electronic properties of carbon nanotubes. Science 2000, 287, 1801–1804. [Google Scholar] [CrossRef]
- Alam, M. Reliability- and process-variation aware design of integrated circuits. Microelectron. Reliab. 2008, 48, 1114–1122. [Google Scholar] [CrossRef]
- Lee, Y.H.; McMahon, W.; Mielke, N.; Lu, Y.L.R.; Walstra, S. Managing bias-temperature instability for product reliability. Proc. Int. Symp. VLSI Technol. 2007, 1, 52–53. [Google Scholar]
- Moore, G.E. Cramming more components onto integrated circuits (Reprinted from Electronics, pg 114–117, April 19, 1965). Proc. IEEE 1998, 86, 82–85. [Google Scholar] [CrossRef]
- Kang, S.J.; Kocabas, C.; Ozel, T.; Shim, M.; Pimparkar, N.; Alam, M.A.; Rotkin, S.V.; Rogers, J.A. High-performance electronics using dense, perfectly aligned arrays of single-walled carbon nanotubes. Nat. Nanotechnol. 2007, 2, 230–236. [Google Scholar] [CrossRef]
- Patil, N.; Lin, A.; Myers, E.R.; Ryu, K.; Badmaev, A.; Zhou, C.W.; Wong, H.S.P.; Mitra, S. Wafer-scale growth and transfer of aligned single-walled carbon nanotubes. IEEE Trans. Nanotechnol. 2009, 8, 498–504. [Google Scholar] [CrossRef]
- Wang, C.; Badmaev, A.; Jooyaie, A.; Bao, M.Q.; Wang, K.L.; Galatsis, K.; Zhou, C.W. Radio frequency and linearity performance of transistors using high-purity semiconducting carbon nanotubes. ACS Nano 2011, 5, 4169–4176. [Google Scholar] [CrossRef]
- Cao, Q.; Han, S.-J.; Tulevski, G.S.; Franklin, A.D.; Haensch, W. Evaluation of field-effect mobility and contact resistance of transistors that use solution-processed single-walled carbon nanotubes. ACS Nano 2012, 6, 6471–6477. [Google Scholar] [CrossRef]
- Vijayaraghavan, A.; Blatt, S.; Weissenberger, D.; Oron-Carl, M.; Hennrich, F.; Gerthsen, D.; Hahn, H.; Krupke, R. Ultra-large-scale directed assembly of single-walled carbon nanotube devices. Nano Lett. 2007, 7, 1556–1560. [Google Scholar] [CrossRef]
- Bardecker, J.A.; Afzali, A.; Tulevski, G.S.; Graham, T.; Hannon, J.B.; Jen, A.K.Y. Directed assembly of single-walled carbon nanotubes via drop-casting onto a UV-patterned photosensitive monolayer. J. Am. Chem. Soc. 2008, 130, 7226–7227. [Google Scholar] [CrossRef]
- Park, H.; Afzali, A.; Han, S.-J.; Tulevski, G.S.; Franklin, A.D.; Tersoff, J.; Hannon, J.B.; Haensch, W. High-density integration of carbon nanotubes via chemical self-assembly. Nat. Nanotechnol. 2012, 7, 787–791. [Google Scholar] [CrossRef]
- Cao, J.; Nyffeler, C.; Lister, K.; Ionescu, A.M. Resist-assisted assembly of single-walled carbon nanotube devices with nanoscale precision. Carbon 2012, 50, 1720–1726. [Google Scholar] [CrossRef]
- Wang, J. Carbon-nanotube based electrochemical biosensors: A review. Electroanalysis 2005, 17, 7–14. [Google Scholar] [CrossRef]
- Javey, A.; Guo, J.; Farmer, D.B.; Wang, Q.; Wang, D.W.; Gordon, R.G.; Lundstrom, M.; Dai, H.J. Carbon nanotube field-effect transistors with integrated ohmic contacts and high-k gate dielectrics. Nano Lett. 2004, 4, 447–450. [Google Scholar] [CrossRef]
- Cao, Q.; Han, S.-J.; Tulevski, G.S.; Zhu, Y.; Lu, D.D.; Haensch, W. Arrays of single-walled carbon nanotubes with full surface coverage for high-performance electronics. Nat. Nanotechnol. 2013, 8, 180–186. [Google Scholar] [CrossRef]
- Franklin, A.D.; Wong, H.S.P.; Lin, A.; Chen, Z.H. Current scaling in aligned carbon nanotube array transistors with local bottom gating. IEEE Electron Device Lett. 2010, 31, 644–646. [Google Scholar] [CrossRef]
- Cao, J.; Ionescu, A.M. Self-aligned lateral dual-gate suspended-body single-walled carbon nanotube field-effect transistors. Appl. Phys. Lett. 2012, 100, 063103:1–063103:3. [Google Scholar]
- Franklin, A.D.; Koswatta, S.O.; Farmer, D.B.; Smith, J.T.; Gignac, L.; Breslin, C.M.; Han, S.-J.; Tulevski, G.S.; Miyazoe, H.; Haensch, W.; et al. Carbon nanotube complementary wrap-gate transistors. Nano Lett. 2013, 13, 2490–2495. [Google Scholar] [CrossRef]
- Pimparkar, N.; Alam, M.A. A “bottom-up” redefinition for mobility and the effect of poor tube-tube contact on the performance of CNT nanonet thin-film transistors. IEEE Electron Device Lett. 2008, 29, 1037–1039. [Google Scholar] [CrossRef]
- Pimparkar, N.; Guo, J.; Alam, M.A. Performance assessment of subpercolating nanobundle network thin-film transistors by an analytical model. IEEE Trans. Electron Devices 2007, 54, 637–644. [Google Scholar] [CrossRef]
- Raychowdhury, A.; de, V.K.; Kurtin, J.; Borkar, S.Y.; Roy, K.; Keshavarzi, A. Variation tolerance in a multichannel carbon-nanotube transistor for high-speed digital circuits. IEEE Trans. Electron Devices 2009, 56, 383–392. [Google Scholar] [CrossRef]
- Nessim, G.D. Properties, synthesis, and growth mechanisms of carbon nanotubes with special focus on thermal chemical vapor deposition. Nanoscale 2010, 2, 1306–1323. [Google Scholar] [CrossRef]
- Cao, Q.; Rogers, J.A. Ultrathin films of single-walled carbon nanotubes for electronics and sensors: A review of fundamental and applied aspects. Adv. Mater. 2009, 21, 29–53. [Google Scholar] [CrossRef]
- Islam, A.E.; Du, F.; Ho, X.; Jin, S.H.; Dunham, S.; Rogers, J.A. Effect of variations in diameter and density on the statistics of aligned array carbon-nanotube field effect transistors. J. Appl. Phys. 2012, 111, 054511:1–054511:7. [Google Scholar]
- Salamat, S.; Ho, X.N.; Rogers, J.A.; Alam, M.A. Intrinsic performance variability in aligned array CNFETs. IEEE Trans. Nanotechnol. 2011, 10, 439–444. [Google Scholar] [CrossRef]
- Sarker, B.K.; Shekhar, S.; Khondaker, S.I. Semiconducting enriched carbon nanotube aligned arrays of tunable density and their electrical transport properties. ACS Nano 2011, 5, 6297–6305. [Google Scholar] [CrossRef]
- Kocabas, C.; Kim, H.-S.; Banks, T.; Rogers, J.A.; Pesetski, A.A.; Baumgardner, J.E.; Krishnaswamy, S.V.; Zhang, H. Radio frequency analog electronics based on carbon nanotube transistors. Proc. Natl. Acad. Sci. USA 2008, 105, 1405–1409. [Google Scholar] [CrossRef]
- Hong, S.W.; Banks, T.; Rogers, J.A. Improved density in aligned arrays of single-walled carbon nanotubes by sequential chemical vapor deposition on quartz. Adv. Mater. 2010, 22, 1826–1830. [Google Scholar] [CrossRef]
- Xiao, J.L.; Dunham, S.; Liu, P.; Zhang, Y.W.; Kocabas, C.; Moh, L.; Huang, Y.G.; Hwang, K.C.; Lu, C.; Huang, W.; et al. Alignment controlled growth of single-walled carbon nanotubes on quartz substrates. Nano Lett. 2009, 9, 4311–4319. [Google Scholar] [CrossRef]
- Arnold, M.S.; Green, A.A.; Hulvat, J.F.; Stupp, S.I.; Hersam, M.C. Sorting carbon nanotubes by electronic structure using density differentiation. Nat. Nanotechnol. 2006, 1, 60–65. [Google Scholar] [CrossRef]
- Heller, D.A.; Mayrhofer, R.M.; Baik, S.; Grinkova, Y.V.; Usrey, M.L.; Strano, M.S. Concomitant length and diameter separation of single-walled carbon nanotubes. J. Am. Chem. Soc. 2004, 126, 14567–14573. [Google Scholar] [CrossRef]
- Zheng, M.; Jagota, A.; Strano, M.S.; Santos, A.P.; Barone, P.; Chou, S.G.; Diner, B.A.; Dresselhaus, M.S.; McLean, R.S.; Onoa, G.B.; et al. Structure-based carbon nanotube sorting by sequence-dependent DNA assembly. Science 2003, 302, 1545–1548. [Google Scholar] [CrossRef]
- Stokes, P.; Khondaker, S.I. High quality solution processed carbon nanotube transistors assembled by dielectrophoresis. Appl. Phys. Lett. 2010, 96, 083110:1–083110:3. [Google Scholar]
- Jin, S.H.; Dunham, S.N.; Song, J.; Xie, X.; Kim, J.-H.; Lu, C.; Islam, A.; Du, F.; Kim, J.; Felts, J.; et al. Using nanoscale thermocapillary flows to create arrays of purely semiconducting single-walled carbon nanotubes. Nat. Nanotechnol. 2013, 8, 347–355. [Google Scholar] [CrossRef]
- Shulaker, M.M.; Wei, H.; Patil, N.; Provine, J.; Chen, H.Y.; Wong, H.S.P.; Mitra, S. Linear increases in carbon nanotube density through multiple transfer technique. Nano Lett. 2011, 11, 1881–1886. [Google Scholar] [CrossRef]
- Wang, C.; Ryu, K.; de Arco, L.G.; Badmaev, A.; Zhang, J.; Lin, X.; Che, Y.; Zhou, C. Synthesis and device applications of high-density aligned carbon nanotubes using low-pressure chemical vapor deposition and stacked multiple transfer. Nano Res. 2010, 3, 831–842. [Google Scholar] [CrossRef]
- Kim, W.; Javey, A.; Tu, R.; Cao, J.; Wang, Q.; Dai, H.J. Electrical contacts to carbon nanotubes down to 1 nm in diameter. Appl. Phys. Lett. 2005, 87, 173101:1–173101:3. [Google Scholar]
- Tseng, Y.C.; Phoa, K.; Carlton, D.; Bokor, J. Effect of diameter variation in a large set of carbon nanotube transistors. Nano Lett. 2006, 6, 1364–1368. [Google Scholar] [CrossRef]
- Chen, Z.H.; Appenzeller, J.; Knoch, J.; Lin, Y.M.; Avouris, P. The role of metal-nanotube contact in the performance of carbon nanotube field-effect transistors. Nano Lett. 2005, 5, 1497–1502. [Google Scholar] [CrossRef]
- Nosho, Y.; Ohno, Y.; Kishimoto, S.; Mizutani, T. n-Type carbon nanotube field-effect transistors fabricated by using Ca contact electrodes. Appl. Phys. Lett. 2005, 86, 073105:1–073105:3. [Google Scholar]
- Wang, S.; Zeng, Q.S.; Yang, L.J.; Zhang, Z.Y.; Wang, Z.X.; Pei, T.A.; Ding, L.; Liang, X.L.; Gao, M.; Li, Y.; et al. High-performance carbon nanotube light-emitting diodes with Asymmetric contacts. Nano Lett. 2011, 11, 23–29. [Google Scholar] [CrossRef]
- Wei, H.; Chen, H.-Y.; Liyanage, L.; Wong, H.S.P.; Mitra, S. Air-Stable Technique for Fabricating n-Type Carbon Nanotube FETs. In Proceedings of the IEEE International Electron Devices Meeting, Washington DC, USA, 5–7 December, 2011; pp. 505–508.
- Franklin, A.D.; Chen, Z.H. Length scaling of carbon nanotube transistors. Nat. Nanotechnol. 2010, 5, 858–862. [Google Scholar] [CrossRef]
- Franklin, A.D.; Luisier, M.; Han, S.-J.; Tulevski, G.; Breslin, C.M.; Gignac, L.; Lundstrom, M.S.; Haensch, W. Sub-10 nm carbon nanotube transistor. Nano Lett. 2012, 12, 758–762. [Google Scholar] [CrossRef]
- Lin, Y.M.; Appenzeller, J.; Avouris, P. Novel Carbon Nanotube FET Design with Tunable Polarity. In Proceedings of the IEEE International Electron Devices Meeting, SanFrancisco, CA, 13–15 December, 2004; pp. 687–690.
- Sze, S.M. Physics of Semiconductor Devices, 2nd ed.; John Wiley & Sons: Hoboken, NY, USA, 1981. [Google Scholar]
- Ho, X.; Ye, L.; Rotkin, S.V.; Cao, Q.; Unarunotai, S.; Salamat, S.; Alam, M.A.; Rogers, J.A. Scaling properties in transistors that use aligned arrays of single-walled carbon nanotubes. Nano Lett. 2010, 10, 499–503. [Google Scholar] [CrossRef]
- Deshpande, V.V.; Chandra, B.; Caldwell, R.; Novikov, D.S.; Hone, J.; Bockrath, M. Mott insulating state in ultraclean carbon nanotubes. Science 2009, 323, 106–110. [Google Scholar] [CrossRef]
- Charlier, J.C.; Blase, X.; Roche, S. Electronic and transport properties of nanotubes. Rev. Mod. Phys. 2007, 79, 677–732. [Google Scholar] [CrossRef]
- Wahab, M.A.; Jin, S.H.; Islam, A.E.; Kim, J.; Kim, J.-H.; Yeo, W.-H.; Lee, D.J.; Chung, H.U.; Rogers, J.A.; Alam, M.A. Electrostatic dimension of aligned-array carbon nanotube field-effect transistors. ACS Nano 2013, 7, 1299–1308. [Google Scholar] [CrossRef]
- Rutherglen, C.; Jain, D.; Burke, P. Nanotube electronics for radiofrequency applications. Nat. Nanotechnol. 2009, 4, 811–819. [Google Scholar] [CrossRef]
- Ryu, K.; Badmaev, A.; Wang, C.; Lin, A.; Patil, N.; Gomez, L.; Kumar, A.; Mitra, S.; Wong, H.S.P.; Zhou, C.W. CMOS-analogous wafer-scale nanotube-on-insulator approach for submicrometer devices and integrated circuits using aligned nanotubes. Nano Lett. 2009, 9, 189–197. [Google Scholar] [CrossRef]
- Ishikawa, F.N.; Chang, H.K.; Ryu, K.; Chen, P.C.; Badmaev, A.; de Arco, L.G.; Shen, G.Z.; Zhou, C.W. Transparent electronics based on transfer printed aligned carbon nanotubes on rigid and flexible substrates. ACS Nano 2009, 3, 73–79. [Google Scholar] [CrossRef]
- Feng, C.; Liu, K.; Wu, J.S.; Liu, L.; Cheng, J.S.; Zhang, Y.Y.; Sun, Y.H.; Li, Q.Q.; Fan, S.S.; Jiang, K.L. Flexible, stretchable, transparent conducting films made from superaligned carbon nanotubes. Adv. Funct. Mater. 2010, 20, 885–891. [Google Scholar] [CrossRef]
- Ago, H.; Imamoto, K.; Ishigami, N.; Ohdo, R.; Ikeda, K.-I.; Tsuji, M. Competition and cooperation between lattice-oriented growth and step-templated growth of aligned carbon nanotubes on sapphire. Appl. Phys. Lett. 2007, 90, 123112:1–123112:3. [Google Scholar]
- Ismach, A.; Segev, L.; Wachtel, E.; Joselevich, E. Atomic-step-templated formation of single wall carbon nanotube patterns. Angew. Chem. Int. Ed. 2004, 43, 6140–6143. [Google Scholar] [CrossRef]
- Kocabas, C.; Kang, S.J.; Ozel, T.; Shim, M.; Rogers, J.A. Improved synthesis of aligned arrays of single-walled carbon nanotubes and their implementation in thin film type transistors. J. Phys. Chem. C 2007, 111, 17879–17886. [Google Scholar] [CrossRef]
- Huang, H.J.; Maruyama, R.; Noda, K.; Kajiura, H.; Kadono, K. Preferential destruction of metallic single-walled carbon nanotubes by laser irradiation. J. Phys. Chem. B 2006, 110, 7316–7320. [Google Scholar]
- Collins, P.C.; Arnold, M.S.; Avouris, P. Engineering carbon nanotubes and nanotube circuits using electrical breakdown. Science 2001, 292, 706–709. [Google Scholar] [CrossRef]
- Chen, C.X.; Yan, L.J.; Kong, E.S.W.; Zhang, Y.F. Ultrasonic nanowelding of carbon nanotubes to metal electrodes. Nanotechnology 2006, 17, 2192–2197. [Google Scholar] [CrossRef]
- Perebeinos, V.; Avouris, P. Impact excitation by hot carriers in carbon nanotubes. Phy. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Liao, A.; Zhao, Y.; Pop, E. Avalanche-induced current enhancement in semiconducting carbon nanotubes. Phys. Rev. Lett. 2008, 101, 256804. [Google Scholar] [CrossRef]
- Kim, W.; Javey, A.; Vermesh, O.; Wang, O.; Li, Y.M.; Dai, H.J. Hysteresis caused by water molecules in carbon nanotube field-effect transistors. Nano Lett. 2003, 3, 193–198. [Google Scholar] [CrossRef]
- Polishchuk, I.; Ranade, P.; King, T.J.; Hu, C.M. Dual work function metal gate CMOS technology using metal interdiffusion. IEEE Electron Device Lett. 2001, 22, 444–446. [Google Scholar] [CrossRef]
- Lim, A.E.J.; Hwang, W.S.; Wang, X.P.; Lai, D.M.Y.; Samudra, G.S.; Kwong, D.L.; Yeo, Y.C. Metal-gate work function modulation using hafnium alloys obtained by the interdiffusion of thin metallic layers. J. Electrochem. Soc. 2007, 154, H309–H313. [Google Scholar] [CrossRef]
- Franklin, A.D.; Tulevski, G.S.; Han, S.-J.; Shahrjerdi, D.; Cao, Q.; Chen, H.-Y.; Wong, H.S.P.; Haensch, W. Variability in carbon nanotube transistors: Improving device-to-device consistency. ACS Nano 2012, 6, 1109–1115. [Google Scholar] [CrossRef]
- Paul, B.C.; Fujita, S.; Okajima, M.; Lee, T.H.; Wong, H.S.P.; Nishi, Y. Impact of a process variation on nanowire and nanotube device performance. IEEE Trans. Electron Devices 2007, 54, 2369–2376. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Mitra, S.; Akinwande, D.; Beasley, C.; Chai, Y.; Chen, H.-Y.; Chen, X.; Close, G.; Deng, J.; Hazeghi, A.; et al. Carbon Nanotube Electronics—Materials, Devices, Circuits, Design, Modeling, and Performance Projection. In Proceedings of the IEEE International Electron Devices Meeting, Washington DC, USA, 5–7 December, 2011; pp. 501–504.
- Balijepalli, A.; Sinha, S.; Cao, Y. Compact Modeling of Carbon Nanotube Transistor for Early Stage Process-Design Exploration. In Proceedings of the 2007 ACM/IEEE International Symposium on Low Power Electronics and Design (ISLPED), Portland, OR, USA, 27–29 August 2007.
- Zhang, G.; Qi, P.; Wang, X.; Lu, Y.; Li, X.; Tu, R.; Bangsaruntip, S.; Mann, D.; Zhang, L.; Dai, H. Selective etching of metallic carbon nanotubes by gas-phase reaction. Science 2006, 314, 974–977. [Google Scholar] [CrossRef]
- Zhang, J.; Patil, N.P.; Hazeghi, A.; Wong, H.S.P.; Mitra, S. Characterization and design of Logic circuits in the presence of carbon nanotube density variations. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2011, 30, 1103–1113. [Google Scholar] [CrossRef]
- Boslaugh, S.; Watters, P.A. Safari Tech Books Online. In Statistics in a Nutshell; OʼReilly Media: Sebastopol, CA, USA, 2008. [Google Scholar]
- Sun, Y.; Tuleski, G.; Han, S.-J.; Haensch, W.; Chen, Z. Improve Variability in Carbon Nanotube FETs by Scaling. In Proceedings of the Device Research Conference, NotreDame, IN, USA, 21–23 June, 2010; pp. 283–284.
- Jin, S.H.; Islam, A.E.; Kim, T.-I.; Kim, J.-H.; Alam, M.A.; Rogers, J.A. Sources of hysteresis in carbon nanotube field-effect transistors and their elimination via methylsiloxane encapsulants and optimized growth. Adv. Funct. Mater. 2012, 22, 2276–2284. [Google Scholar] [CrossRef]
- Qu, M.; Qiu, Z.-J.; Zhang, Z.-B.; Li, H.; Li, J.; Zhang, S.-L. Charge-injection-induced time decay in carbon nanotube network-based FETs. IEEE Electron Device Lett. 2010, 31, 1098–1100. [Google Scholar] [CrossRef]
- Peng, N.; Zhang, Q.; Yuan, S.; Li, H.; Tian, J.; Chan, L. Current instability of carbon nanotube field effect transistors. Nanotechnology 2007, 18. [Google Scholar] [CrossRef]
- Ellison, M.D.; Crotty, M.J.; Koh, D.; Spray, R.L.; Tate, K.E. Adsorption of NH3 and NO2 on single-walled carbon nanotubes. J. Phys. Chem. B 2004, 108, 7938–7943. [Google Scholar] [CrossRef]
- Yao, Z.; Postma, H.W.C.; Balents, L.; Dekker, C. Carbon nanotube intramolecular junctions. Nature 1999, 402, 273–276. [Google Scholar] [CrossRef]
- Robinson, J.A.; Snow, E.S.; Badescu, S.C.; Reinecke, T.L.; Perkins, F.K. Role of defects in single-walled carbon nanotube chemical sensors. Nano Lett. 2006, 6, 1747–1751. [Google Scholar] [CrossRef]
- Zhou, C.W.; Kong, J.; Yenilmez, E.; Dai, H.J. Modulated chemical doping of individual carbon nanotubes. Science 2000, 290, 1552–1555. [Google Scholar] [CrossRef]
- Zhuravlev, L.T. The surface chemistry of amorphous silica. Zhuravlev model. Colloids Surfaces Physicochem. Eng. Asp. 2000, 173, 1–38. [Google Scholar] [CrossRef]
- Chakrapani, V.; Anderson, A.B.; Wolter, S.D.; Stoner, B.R.; Sumanasekera, G.U.; Angus, J.C. Charge transfer equilibria between diamond and an aqueous oxygen electrochemical redox couple. Science 2007, 318, 1424–1430. [Google Scholar] [CrossRef]
- McGill, S.A.; Rao, S.G.; Manandhar, P.; Xiong, P.; Hong, S. High-performance, hysteresis-free carbon nanotube field-effect transistors via directed assembly. Appl. Phys. Lett. 2006, 89, 163123:1–163123:3. [Google Scholar]
- Aguirre, C.M.; Levesque, P.L.; Paillet, M.; Lapointe, F.; St-Antoine, B.C.; Desjardins, P.; Martel, R. The role of the oxygen/water redox couple in suppressing electron conduction in field-effect transistors. Adv. Mater. 2009, 21. [Google Scholar] [CrossRef]
- Levesque, P.L.; Sabri, S.S.; Aguirre, C.M.; Guillemette, J.; Siaj, M.; Desjardins, P.; Szkopek, T.; Martel, R. Probing charge transfer at surfaces using graphene transistors. Nano Lett. 2011, 11, 132–137. [Google Scholar] [CrossRef]
- Weitz, R.T.; Zschieschang, U.; Effenberger, F.; Klauk, H.; Burghard, M.; Kern, K. High-performance carbon nanotube field effect transistors with a thin gate dielectric based on a self-assembled monolayer. Nano Lett. 2007, 7, 22–27. [Google Scholar] [CrossRef]
- Hur, S.H.; Yoon, M.H.; Gaur, A.; Shim, M.; Facchetti, A.; Marks, T.J.; Rogers, J.A. Organic nanodielectrics for low voltage carbon nanotube thin film transistors and complementary logic gates. J. Am. Chem. Soc. 2005, 127, 13808–13809. [Google Scholar]
- Reisman, A.; Williams, C.K.; Maldonado, J.R. Generation and annealing of defects in silicon dioxide. J. Appl. Phys. 1987, 62, 868–874. [Google Scholar] [CrossRef]
- Alam, M.A. SILC as a measure of trap generation and predictor of T-BD in ultrathin oxides. IEEE Trans. Electron Devices 2002, 49, 226–231. [Google Scholar] [CrossRef]
- Solomon, P. Breakdown in silicon-oxide. J. Vac. Sci. Technol. 1977, 14, 1122–1130. [Google Scholar] [CrossRef]
- Ribes, G.; Mitard, J.; Denais, M.; Bruyere, S.; Monsieur, F.; Parthasarathy, C.R.; Vincent, E.; Ghibaudo, G. Review on high-k dielectrics reliability issues. IEEE Trans. Device Mater Reliab. 2005, 5, 5–19. [Google Scholar] [CrossRef]
- Lenahan, P.M.; Dressendorfer, P.V. Hole traps and trivalent silicon centers in metal-oxide silicon devices. J. Appl. Phys. 1984, 55, 3495–3499. [Google Scholar] [CrossRef]
- Lenahan, P.M. Dominating defects in the MOS system: Pb and E' centers. In Defects in Microelectronic Materials and Devices; Fleetwood, S.P.D., Schrimpf, R.D., Eds.; CRC Press: Taylor and Francis Group, Boca Raton, FL, USA, 2009; pp. 163–214. [Google Scholar]
- Skuja, L. Optically active oxygen-deficiency-related centers in amorphous silicon dioxide. J. Non Cryst. Solids 1998, 239, 16–48. [Google Scholar] [CrossRef]
- Spinelli, A.S.; Lacaita, A.L.; Rigamonti, M.; Ielmini, D.; Ghidini, G. Separation of electron and hole traps by transient current analysis. Microelectron. Eng. 1999, 48, 151–154. [Google Scholar] [CrossRef]
- Hongo, H.; Nihey, F.; Yorozu, S. Relationship between carbon nanotube density and hysteresis characteristics of carbon nanotube random network-channel field effect transistors. J. Appl. Phys. 2010, 107, 094501:1–094501:9. [Google Scholar]
- Di Bartolomeo, A.; Rinzan, M.; Boyd, A.K.; Yang, Y.; Guadagno, L.; Giubileo, F.; Barbara, P. Electrical properties and memory effects of field-effect transistors from networks of single- and double-walled carbon nanotubes. Nanotechnology 2010, 21. [Google Scholar] [CrossRef]
- Memming, R. Semiconductor Electrochemistry; Wiley-VCH: Weinheim, NY, USA, 2001. [Google Scholar]
- Shockley, W.; Read, W.T. Statistics of the recombinations of holes and electrons. Phys. Rev. 1952, 87, 835–842. [Google Scholar] [CrossRef]
- Chang, M.H.; Zhang, J.F.; Zhang, W.D. Assessment of capture cross sections and effective density of electron traps generated in silicon dioxides. IEEE Trans. Electron Devices 2006, 53, 1347–1354. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, C.; Fasoli, A.; Scardaci, V.; Pisana, S.; Hasan, T.; Robertson, J.; Milne, W.I.; Ferrari, A.C. Hysteresis suppression in self-assembled single-wall nanotube field effect transistors. Phys. ELowDimens. Syst. Nanostruct. 2008, 40, 2278–2282. [Google Scholar] [CrossRef]
- Kim, S.K.; Xuan, Y.; Ye, P.D.; Mohammadi, S.; Back, J.H.; Shim, M. Atomic layer deposited Al2O3 for gate dielectric and passivation layer of single-walled carbon nanotube transistors. Appl. Phys. Lett. 2007, 90, 163108:1–163108:3. [Google Scholar]
- Kirton, M.J.; Uren, M.J. Noise in solid-state microstructures—A new perspective on individual defects, interface states and low-frequency (1/f) noise. Adv. Phys. 1989, 38, 367–468. [Google Scholar] [CrossRef]
- Vandamme, L.K.J. Noise as a diagnostic tool for quality and reliability of electronic devices. IEEE Trans. Electron Devices 1994, 41, 2176–2187. [Google Scholar] [CrossRef]
- Vandamme, L.K.J.; Li, X.S.; Rigaud, D. 1/f Noise in MOS Devices, Mobility or Number Fluctuations. IEEE Trans. Electron Devices 1994, 41, 1936–1945. [Google Scholar] [CrossRef]
- Weissman, M.B. 1/f noise and other slow, nonexponential kinetics in condensed matter. Rev. Mod. Phys. 1988, 60, 537–571. [Google Scholar] [CrossRef]
- Weissman, M.B. Low-frequency noise as a tool to study disordered materials. Annu. Rev. Mater. Sci. 1996, 26, 395–429. [Google Scholar] [CrossRef]
- Kurata, H.; Otsuga, K.; Kotabe, A.; Kajiyama, S.; Osabe, T.; Sasago, Y.; Narumi, S.; Tokami, K.; Kamohara, S.; Tsuchiya, O. Random telegraph signal in flash memory: Its impact on scaling of multilevel flash memory beyond the 90-nm node. IEEE J. SolidState Circuits 2007, 42, 1362–1369. [Google Scholar] [CrossRef]
- Ghetti, A.; Compagnoni, C.M.; Biancardi, F.; Lacaita, A.L.; Beltrami, S.; Chiavarone, L.; Spinelli, A.S.; Visconti, A. Scaling trends for random telegraph noise in deca-nanometer Flash memories. In Proceedings of the IEEE International Electron Devices Meeting Technical Digest, SanFrancisco, CA, 15–17 December, 2008; pp. 835–838.
- Gierkink, S.L.J.; Klumperink, E.A.M.; van der Wel, A.P.; Hoogzaad, G.; van Tuijl, E.; Nauta, B. Intrinsic 1/f device noise reduction and its effect on phase noise in CMOS ring oscillators. IEEE J. SolidState Circuits 1999, 34, 1022–1025. [Google Scholar] [CrossRef]
- Cao, Q.; Xia, M.G.; Kocabas, C.; Shim, M.; Rotkin, S.V.; Rogers, J.A. Gate capacitance coupling of singled-walled carbon nanotube thin-film transistors. Appl. Phys. Lett. 2007, 90, 023516:1–023516:3. [Google Scholar]
- Rosenblatt, S.; Yaish, Y.; Park, J.; Gore, J.; Sazonova, V.; McEuen, P.L. High performance electrolyte gated carbon nanotube transistors. Nano Lett. 2002, 2, 869–872. [Google Scholar] [CrossRef]
- Vitusevich, S.A.; Sydoruk, V.A.; Petrychuk, M.V.; Danilchenko, B.A.; Klein, N.; Offenhaeusser, A.; Ural, A.; Bosman, G. Transport properties of single-walled carbon nanotube transistors after gamma radiation treatment. J. Appl. Phys. 2010, 107, 063701:1–063701:6. [Google Scholar]
- Lin, Y.-M.; Appenzeller, J.; Knoch, J.; Chen, Z.; Avouris, P. Low-frequency current fluctuations in individual semiconducting single-wall carbon nanotubes. Nano Lett. 2006, 6, 930–936. [Google Scholar] [CrossRef] [Green Version]
- Collins, P.G.; Fuhrer, M.S.; Zettl, A. 1/f noise in carbon nanotubes. Appl. Phys. Lett. 2000, 76, 894–896. [Google Scholar] [CrossRef]
- Snow, E.S.; Novak, J.P.; Lay, M.D.; Perkins, F.K. 1/f noise in single-walled carbon nanotube devices. Appl. Phys. Lett. 2004, 85, 4172–4174. [Google Scholar] [CrossRef]
- Liu, F.; Wang, K.L.; Li, C.; Zhou, C. Study of random telegraph signals in single-walled carbon nanotube field effect transistors. IEEE Trans. Nanotechnol. 2006, 5, 441–445. [Google Scholar] [CrossRef]
- Vitusevich, S.; Gasparyan, F. Low-Frequency Noise Spectroscopy at Nanoscale: Carbon Nanotube Materials and Devices. Available online: http://cdn.intechweb.org/pdfs/17294.pdf (accessed on 1 July 2013).
- Veksler, D.; Bersuker, G.; Rumyantsev, S.; Shur, M.; Park, H.; Young, C.; Lim, K.Y.; Taylor, W.; Jammy, R.; IEEE. Understanding noise measurements in MOSFETs: The role of traps structural relaxation. In Proceedings of the International Reliability Physics Symposium, Anaheim, CA, 2–6 May, 2010; pp. 73–79.
- Hooge, F.N. 1/F noise sources. IEEE Trans. Electron Devices 1994, 41, 1926–1935. [Google Scholar] [CrossRef]
- Liu, F.; Bao, M.; Wang, K.L.; Zhang, D.; Zhou, C. Coulomb attractive random telegraph signal in a single-walled carbon nanotube. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Liu, F.; Wang, K.L. Correlated random telegraph signal and low-frequency noise in carbon nanotube transistors. Nano Lett. 2008, 8, 147–151. [Google Scholar] [CrossRef]
- Liu, F.; Wang, K.L.; Zhang, D.; Zhou, C. Random telegraph signals and noise behaviors in carbon nanotube transistors. Appl. Phys. Lett. 2006, 89, 243101:1–243101:3. [Google Scholar]
- Chan, J.; Kidd, D.; Burke, B.; Harriott, L.; Williams, K. Noise analysis of carbon nanotube field effect transistors irradiated by electron beam. J. Vac. Sci. Technol. B 2010, 28, C6P66–C6P69. [Google Scholar] [CrossRef]
- Cress, C.D.; McMorrow, J.J.; Robinson, J.T.; Friedman, A.L.; Hughes, H.L.; Weaver, B.D.; Landi, B.J. Total ionizing dose-hardened carbon nanotube thin-film transistors with silicon oxynitride gate dielectrics. MRS Commun. 2011, 1, 27–31. [Google Scholar] [CrossRef]
- Cress, C.D.; McMorrow, J.J.; Robinson, J.T.; Friedman, A.L.; Landi, B.J. Radiation effects in single-walled carbon nanotube thin-film-transistors. IEEE Trans. Nucl. Sci. 2010, 57, 3040–3045. [Google Scholar]
- Hulman, M.; Skakalova, V.; Roth, S.; Kuzmany, H. Raman spectroscopy of single-wall carbon nanotubes and graphite irradiated by gamma rays. J. Appl. Phys. 2005, 98, 024311:1–024311:5. [Google Scholar]
- Rossi, J.E.; Cress, C.D.; Helenic, A.R.; Schauerman, C.M.; DiLeo, R.A.; Cox, N.D.; Messenger, S.R.; Weaver, B.D.; Hubbard, S.M.; Landi, B.J. Ion irradiation of electronic-type-separated single wall carbon nanotubes: A model for radiation effects in nanostructured carbon. J. Appl. Phys. 2012, 112, 034314:1–034314:11. [Google Scholar]
- Tang, X.W.; Yang, Y.; Kim, W.; Wang, Q.; Qi, P.F.; Dai, H.J.; Xing, L. Measurement of ionizing radiation using carbon nanotube field effect transistor. Phys. Med. Biol. 2005, 50, N23–N31. [Google Scholar] [CrossRef]
- Cress, C.D.; Schauerman, C.M.; Landi, B.J.; Messenger, S.R.; Raffaelle, R.P.; Walters, R.J. Radiation effects in single-walled carbon nanotube papers. J. Appl. Phys. 2010, 107, 014316:1–014316:5. [Google Scholar]
- Skakalova, V.; Woo, Y.S.; Osvath, Z.; Biro, L.P.; Roth, S. Electron transport in Ar+-irradiated single wall carbon nanotubes. Phys. Status Solidi B 2006, 243, 3346–3350. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Saito, R.; Jorio, A. Raman spectroscopy of carbon nanotubes. Phys. Rep. Rev. Sect. Phys. Lett. 2005, 409, 47–99. [Google Scholar]
- Buchowicz, G.; Stone, P.R.; Robinson, J.T.; Cress, C.D.; Beeman, J.W.; Dubon, O.D. Correlation between structure and electrical transport in ion-irradiated graphene grown on Cu foils. Appl. Phys. Lett. 2010, 98, 032102:1–032102:3. [Google Scholar]
- Hong, W.-K.; Lee, C.; Nepal, D.; Geckeler, K.E.; Shin, K.; Lee, T. Radiation hardness of the electrical properties of carbon nanotube network field effect transistors under high-energy proton irradiation. Nanotechnology 2006, 17, 5675–5680. [Google Scholar] [CrossRef]
- Hughes, H.L.; Benedetto, J.M. Radiation effects and hardening of MOS technology: Devices and circuits. IEEE Trans. Nucl. Sci. 2003, 50, 500–521. [Google Scholar] [CrossRef]
- Islam, A.E.; Kufluoglu, H.; Varghese, D.; Mahapatra, S.; Alam, M.A. Recent issues in negative bias temperature instability: Initial degradation, field-dependence of interface trap generation, hole trapping effects, and relaxation. IEEE Trans. Electron Devices 2007, 54, 2143–2154. [Google Scholar] [CrossRef]
- Schroder, D.K.; Babcock, J.A. Negative bias temperature instability: Road to cross in deep submicron silicon semiconductor manufacturing. J. Appl. Phys. 2003, 94, 1–18. [Google Scholar] [CrossRef]
- Gu, G.; Kane, M.G.; Mau, S.C. Reversible memory effects and acceptor states in pentacene-based organic thin-film transistors. J. Appl. Phys. 2007, 101, 014504:1–014504:9. [Google Scholar]
- Liu, J.; Wang, C.; Tu, X.; Liu, B.; Chen, L.; Zheng, M.; Zhou, C. Chirality-controlled synthesis of single-wall carbon nanotubes using vapour-phase epitaxy. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef]
- Wilk, G.D.; Wallace, R.M.; Anthony, J.M. High-kappa gate dielectrics: Current status and materials properties considerations. J. Appl. Phys. 2001, 89, 5243–5275. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Islam, A.E. Variability and Reliability of Single-Walled Carbon Nanotube Field Effect Transistors. Electronics 2013, 2, 332-367. https://doi.org/10.3390/electronics2040332
Islam AE. Variability and Reliability of Single-Walled Carbon Nanotube Field Effect Transistors. Electronics. 2013; 2(4):332-367. https://doi.org/10.3390/electronics2040332
Chicago/Turabian StyleIslam, Ahmad Ehteshamul. 2013. "Variability and Reliability of Single-Walled Carbon Nanotube Field Effect Transistors" Electronics 2, no. 4: 332-367. https://doi.org/10.3390/electronics2040332
APA StyleIslam, A. E. (2013). Variability and Reliability of Single-Walled Carbon Nanotube Field Effect Transistors. Electronics, 2(4), 332-367. https://doi.org/10.3390/electronics2040332