High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control for Quadrotor Attitude System
Abstract
:1. Introduction
- The ESO in ADRC is improved via robust uniform high-order sliding mode differentiator to achieve fixed time convergence given bounded differential of lumped disturbance.
- A non-linear feedback control law combining a high-order sliding mode with feedback linearization is applied in the improved ADRC scheme. In this way, the attitude controller provides fixed-time stability.
2. Mathematical Models
2.1. Rigid Body Dynamics
2.2. Actuator Mode
2.2.1. Motor Model
2.2.2. Propeller Aerodynamic Model
- Set .
- Solve the equation through the Newton method with initial value in the case of :
- Calculate , go to step 2 and start the next iteration.
2.3. Example of Measuring and Calculating Propeller Aerodynamic Model Parameters
3. Active Disturbance Rejection Control (ADRC) Method
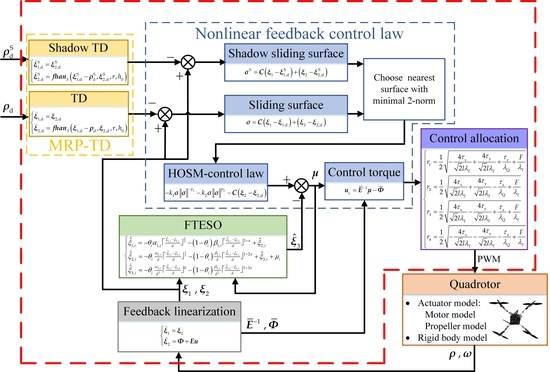
4. High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control (FTADRC)
- Feedback linearization for regularizing the attitude dynamic model;
- Fixed-time extended state observer (FTESO) for observing the unknown disturbances accurately;
- MRP-TD for tracking the differential of input attitude described by MRP;
- Non-linear feedback control law for driving the orientation of quadrotor to track the desired attitude timely;
- Control allocation for generating pulse-width modulation (PWM) signals for motors.
4.1. Feedback Linearization
4.2. Fixed-Time Third-Order Sliding Mode Observer-Based Extended State Observer (ESO)
4.3. Tracking Differentiator
4.4. Multivariable High-Order Sliding Mode (HOSM)-Based Fixed-Time Non-Linear Feedback Law
4.5. Non-Linear Control Allocation
5. Simulation and Experimental Results
5.1. Simulation Results
5.2. Experimental Results
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Design and control of an indoor micro quadrotor. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May; pp. 4393–4398.
- Özbek, N.S.; Önkol, M.; Efe, M.Ö. Feedback control strategies for quadrotor-type aerial robots: A survey. Trans. Inst. Meas. Control 2016, 38, 529–554. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.J. Trajectory tracking control of multirotors from modelling to experiments: A survey. Int. J. Control Autom. Syst. 2017, 15, 281–292. [Google Scholar] [CrossRef]
- Tayebi, A.; McGilvray, S. Attitude stabilization of a vtol quadrotor aircraft. IEEE Trans. Control Syst. Technol. 2006, 14, 562–571. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor aerial vehicles modeling, estimation, and control of quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Pounds, P.; Mahony, R.; Corke, P. Modelling and control of a large quadrotor robot. Control Eng. Practice 2010, 18, 691–699. [Google Scholar] [CrossRef] [Green Version]
- Kendoul, F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems. J. Field Robot. 2012, 29, 315–378. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.J.; Sastry, S. Feedback linearization vs. Adaptive sliding mode control for a quadrotor helicopter. Int. J. Control Autom. Syst. 2009, 7, 419–428. [Google Scholar] [CrossRef]
- Kim, J.; Kang, M.S.; Park, S. Accurate modeling and robust hovering control for a quad-rotor vtol aircraft. In Proceedings of the 2nd International Symposium on UAVs, Reno, NV, USA, June 2009; pp. 9–26. [Google Scholar]
- Lyu, X.M.; Zhou, J.N.; Gu, H.W.; Li, Z.X.; Shen, S.J.; Zhang, F. Disturbance observer based hovering control of quadrotor tail-sitter vtol uavs using h-infinity synthesis. IEEE Robot. Autom. Lett. 2018, 3, 2910–2917. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Output feedback control of a quadrotor uav using neural networks. IEEE Trans. Neural Netw. 2010, 21, 50–66. [Google Scholar] [CrossRef] [PubMed]
- Aboudonia, A.; El-Badawy, A.; Rashad, R. Disturbance observer-based feedback linearization control of an unmanned quadrotor helicopter. Proc. Inst. Mech. Eng. Part I: J. Syst. Control Eng. 2016, 230, 877–891. [Google Scholar] [CrossRef]
- Aboudonia, A.; Rashad, R.; El-Badawy, A. Composite hierarchical anti-disturbance control of a quadrotor uav in the presence of matched and mismatched disturbances. J. Intell. Robot. Syst. 2018, 90, 201–216. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A new disturbance attenuation control scheme for quadrotor unmanned aerial vehicles. IEEE Trans. Ind. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- Ahmed, N.; Chen, M. Sliding mode control for quadrotor with disturbance observer. Adv. Mech. Eng. 2018, 10, 16. [Google Scholar] [CrossRef]
- Benallegue, A.; Mokhtari, A.; Fridman, L. High-order sliding-mode observer for a quadrotor uav. Int. J. Robust Nonlinear Control 2008, 18, 427–440. [Google Scholar] [CrossRef]
- Besnard, L.; Shtessel, Y.B.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Fethalla, N.; Saad, M.; Michalska, H.; Ghommam, J. Robust observer-based dynamic sliding mode conroller for a quadrotor uav. IEEE Access 2018, 6, 45846–45859. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Z.; Chou, W. Super-twisting extended state observer and sliding mode controller for quadrotor uav attitude system in presence of wind gust and actuator faults. Electronics 2018, 7, 128. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Z.; Chou, W. Generalized extended state observer based high precision attitude control of quadrotor vehicles subject to wind disturbance. IEEE Access 2018, 6. [Google Scholar] [CrossRef]
- Han, J. From pid to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wu, Z.-H.; Guo, B.-Z. On convergence of active disturbance rejection control for a class of uncertain stochastic nonlinear systems. Int. J. Control 2017, 1–14. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. Active Disturbance Rejection Control for Nonlinear Systems: An Introduction, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 6–9. [Google Scholar]
- Yang, H.J.; Cheng, L.; Xia, Y.Q.; Yuan, Y. Active disturbance rejection attitude control for a dual closed-loop quadrotor under gust wind. IEEE Trans. Control Syst. Technol. 2018, 26, 1400–1405. [Google Scholar] [CrossRef]
- Ma, D.L.; Xia, Y.Q.; Li, T.Y.; Chang, K. Active disturbance rejection and predictive control strategy for a quadrotor helicopter. IET Contr. Theory Appl. 2016, 10, 2213–2222. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, B.; Zhang, Y. A novel robust attitude control for quadrotor aircraft subject to actuator faults and wind gusts. IEEE/CAA J. Autom. Sinica 2018, 5, 292–300. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Basin, M.; Yu, P.; Shtessel, Y. Finite-and fixed-time differentiators utilising hosm techniques. IET Control Theory Appl. 2016, 11, 1144–1152. [Google Scholar] [CrossRef]
- Menard, T.; Moulay, E.; Perruquetti, W. Fixed-time observer with simple gains for uncertain systems. Automatica 2017, 81, 438–446. [Google Scholar] [CrossRef] [Green Version]
- Angulo, M.T.; Moreno, J.A.; Fridman, L. Robust exact uniformly convergent arbitrary order differentiator. Automatica 2013, 49, 2489–2495. [Google Scholar] [CrossRef]
- Li, P.; Ma, J.; Zheng, Z. Disturbance-observer-based fixed-time second-order sliding mode control of an air-breathing hypersonic vehicle with actuator faults. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2018, 232, 344–361. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Chen, M.; Liu, C. Fixed-time disturbance observer design for brunovsky system. IEEE Trans. Circuit Syst. Part 2: Express Birefs 2018, 65, 341–345. [Google Scholar] [CrossRef]
- Yu, P.; Shtessel, Y.; Edwards, C. Continuous higher order sliding mode control with adaptation of air breathing hypersonic missile. Int. J. Adapt. Control Signal Process. 2016, 30, 1099–1117. [Google Scholar] [CrossRef] [Green Version]
- Basin, M.V.; Yu, P.; Shtessel, Y.B. Hypersonic missile adaptive sliding mode control using finite-and fixed-time observers. IEEE Trans. Ind. Electron. 2018, 65, 930–941. [Google Scholar] [CrossRef]
- Yu, X.; Li, P.; Zhang, Y. The design of fixed-time observer and finite-time fault-tolerant control for hypersonic gliding vehicles. IEEE Trans. Ind. Electron. 2018, 65, 4135–4144. [Google Scholar] [CrossRef]
- Schaub, H.; Junkins, J.L. Stereographic orientation parameters for attitude dynamics: A generalization of the rodrigues parameters. J. Astron. Sci. 1996, 44, 1–19. [Google Scholar]
- Leishman, G.J. Principles of Helicopter Aerodynamics, 2nd ed.; Cambridge university press: Cambridge, UK, 2006; pp. 55–167. [Google Scholar]
- Basin, M.; Panathula, C.B.; Shtessel, Y. Multivariable continuous fixed-time second-order sliding mode control: Design and convergence time estimation. IET Control Theory Appl. 2016, 11, 1104–1111. [Google Scholar] [CrossRef]
- Madgwick, S. An efficient orientation filter for inertial and inertial/magnetic sensor arrays. Report x-io Univ. Bristol 2010, 25, 113–118. [Google Scholar]
































| Parameters | Description | Determination method | |
|---|---|---|---|
| Atmospheric parameter | Air density | 1.2kg/m3 in low altitude | |
| Propeller parameters | Propeller radius | Measuring directly | |
| Blade chord | Measuring directly | ||
| Blade pitch angle | Measuring directly | ||
| Number of rotor blades | Measuring directly | ||
| Velocity parameters | Climb inflow ratio | Calculated according to velocity of quadrotor and wind speed | |
| Advance ratio | Calculated according to velocity of quadrotor and wind speed | ||
| Aerodynamic coefficients | Lift-curve slope | Estimated with trust-rotation speed curve | |
| Drag coefficient | Estimated with torque-rotation speed curve | ||
| Radial Position (mm) | Chord (mm) | Pitch Angle (°) |
|---|---|---|
| 32 | 29 | 35.2 |
| 48 | 40 | 28 |
| 64 | 48 | 21.4 |
| 80 | 52 | 17.6 |
| 96 | 55 | 14.2 |
| 112 | 56 | 12.7 |
| 128 | 55 | 11.3 |
| 144 | 51 | 10.6 |
| 160 | 47 | 6.6 |
| 176 | 38 | 6.0 |
| 192 | 28 | 6.0 |
| 203.2 | 0 | 6.0 |
| Parameter | Description | True Value | Nominal Value |
|---|---|---|---|
| Ix | Inertia along xb-axis | 0.1 kgm2 | 0.05 kgm2 |
| Iy | Inertia along yb-axis | 0.1 kgm2 | 0.05 kgm2 |
| Iz | Inertia along zb-axis | 0.22 kgm2 | 0.5 kgm2 |
| l | Distance between rotor and centroid | 0.4 m | 0.4 m |
| m | Mass | 8 kg | -- |
| Kv | Motor velocity constant | 325 rpm/V | -- |
| Equivalent resistance of motor | 0.26 Ω | -- |
| Parameters | Nominal Value |
|---|---|
| 0.01 kgm2 | |
| 0.01 kgm2 | |
| 0.02 kgm2 | |
| diag(5,5,30) | |
| 70 | |
| 10 | |
| 0.5 | |
| 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Wei, C.; Yang, F.; Cui, N. High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control for Quadrotor Attitude System. Electronics 2018, 7, 357. https://doi.org/10.3390/electronics7120357
Song C, Wei C, Yang F, Cui N. High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control for Quadrotor Attitude System. Electronics. 2018; 7(12):357. https://doi.org/10.3390/electronics7120357
Chicago/Turabian StyleSong, Chunlin, Changzhu Wei, Feng Yang, and Naigang Cui. 2018. "High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control for Quadrotor Attitude System" Electronics 7, no. 12: 357. https://doi.org/10.3390/electronics7120357
APA StyleSong, C., Wei, C., Yang, F., & Cui, N. (2018). High-Order Sliding Mode-Based Fixed-Time Active Disturbance Rejection Control for Quadrotor Attitude System. Electronics, 7(12), 357. https://doi.org/10.3390/electronics7120357