A 6-Bit Ku Band Digital Step Attenuator with Low Phase Variation in 0.13-μm SiGe BiCMOS
Abstract
:1. Introduction
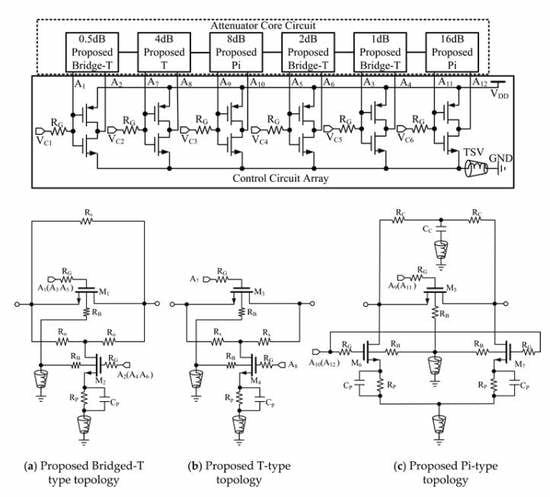
2. Proposed Circuit Design and Analysis
3. Measurement Results
4. Comparison with Relevant Digital Control Step Attenuators
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Sim, S.; Jeon, L.; Kim, J. A compact X-Band Bi-directional phased-array T/R chipset in 0.13 μm CMOS technology. IEEE Trans. Microw. Theory Tech. 2013, 61, 562–569. [Google Scholar] [CrossRef]
- Jeong, J.; Yom, I.; Kim, J.; Lee, W.; Lee, C. A 6–18 GHz GaAs multifunction chip with 8-bit true time delay and 7-bit amplitude control. IEEE Trans. Microw. Theory Tech. 2018, 66, 2220–2230. [Google Scholar] [CrossRef]
- Wagner, J.; Mayer, U.; Wickert, M.; Wolf, R.; Joram, N.; Strobel, A.; Ellinger, F. X-type attenuator in CMOS with novel control linearization, very low phase variations and automatic matching. In Proceedings of the 2013 European Microwave Integrated Circuit Conference, Nuremberg, Germany, 6–8 October 2013; pp. 200–203. [Google Scholar]
- Li, D.; Fei, C.; Wu, X.; Yang, Y. A 6-bit digital CMOS variable gain attenuator with large dynamic range and high linearity-in-dB for ultrasound imaging applications. Microelectron. J. 2019, 83, 32–38. [Google Scholar] [CrossRef]
- Koolivand, Y.; Shoaei, O.; Jafarabadi-Ashtiani, S. Linear in dB, sub 0.2 dB gain-step CMOS programmable gain amplifier for ultrasound applications. Analog Integr. Circuits Signal Process. 2017, 93, 309–318. [Google Scholar] [CrossRef]
- Cho, M.; Song, I.; Fleetwood, Z.E.; Cressler, J.D. A SiGe-BiCMOS wideband active bidirectional digital step attenuator with bandwidth tuning and equalization. IEEE Trans. Microw. Theory Tech. 2018, 66, 3866–3876. [Google Scholar] [CrossRef]
- Mikul, A.O.; Zhu, S.; Sun, P.; You, Y.; Sah, S.P.; Heo, D. Compact low phase imbalance broadband attenuator based on SiGe PIN diode. In Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium Digest, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. [Google Scholar] [CrossRef]
- Eom, H.; Yang, K. A 6–20 GHz compact multi-bit digital attenuator using InP/InGaAs PIN Diodes. In Proceedings of the 2008 20th International Conference on Indium Phosphide and Related Materials, Versailles, France, 25–29 May 2008; pp. 1–3. [Google Scholar] [CrossRef]
- Zhu, S.; Mikul, A.O.; Sun, P.; You, Y.; Kim, J.H.; Kim, B.S.; Heo, D. Inductor-less SiGe pin diode attenuator with low phase variations. Electron. Lett. 2012, 48, 1287–1289. [Google Scholar] [CrossRef]
- Bae, J.; Lee, J.; Nguyen, C. A 10–67-GHz CMOS dual-function switching attenuator with improved flatness and large attenuation range. IEEE Trans. Microw. Theory Tech. 2013, 61, 4118–4129. [Google Scholar] [CrossRef]
- Min, B.; Rebeiz, G.M. A 10–50-GHz CMOS distributed step attenuator with low loss and low phase imbalance. IEEE J. Solid State Circuits 2007, 42, 2547–2554. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C.; Zhang, X.; Wu, Y.; Kang, K. A CMOS K-band 6-bit attenuator with low phase imbalance for phased array applications. IEEE Access 2017, 5, 19657–19661. [Google Scholar] [CrossRef]
- Shi, W.; Ma, K.; Mou, S.; Meng, F. A compact Ku-band 6-bit attenuator in 0.35um SiGe BiCMOS technology. In Proceedings of the 2017 IEEE Electrical Design of Advanced Packaging and Systems Symposium (EDAPS), Haining, China, 14–16 December 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Bae, J.; Nguyen, C. A novel concurrent 22–29/57–64-GHz dual-band CMOS step attenuator with low phase variations. IEEE Trans. Microw. Theory Tech. 2016, 64, 1867–1875. [Google Scholar] [CrossRef]
- Kandis, H.; Yazici, M.; Gurbuz, Y.; Kaynak, M. A wideband (3–13 GHz) 7-Bit SiGe BiCMOS step attenuator with improved flatness. In Proceedings of the 2018 18th Mediterranean Microwave Symposium (MMS), Istanbul, Turkey, 31 October–2 November 2018; pp. 139–142. [Google Scholar] [CrossRef]
- Davulcu, M.; Caliskan, C.; Kalyoncu, I.; Kaynak, M.; Gurbuz, Y. 7-Bit SiGe-BiCMOS step attenuator for X-Band phased-array RADAR applications. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 598–600. [Google Scholar] [CrossRef]
- Sarfraz, M.M.; Ullah, F.; Wang, M.; Zhang, H. A 6-Bit 0.13 μm SiGe BiCMOS digital step attenuator with low phase variation for K-band application. Electronics 2018, 7, 74. [Google Scholar] [CrossRef]
- Ku, B.; Hong, S. 6-bit CMOS digital attenuators with low phase variations for X-band phased-array systems. IEEE Trans. Microw. Theory Tech. 2010, 58, 1651–1663. [Google Scholar] [CrossRef]
- Ciccognani, W.; Giannini, F.; Limiti, E.; Longhi, P.E. Compensating for parasitic phase shift in microwave digitally controlled attenuators. Electron. Lett. 2008, 44, 743–744. [Google Scholar] [CrossRef]
- Sun, P. Analysis of phase variation of CMOS digital attenuator. Electron. Lett. 2014, 50, 1912–1914. [Google Scholar] [CrossRef]
- Song, I.; Cho, M.; Cressler, J.D. Design and analysis of a low loss, wideband digital step attenuator with minimized amplitude and phase variations. IEEE J. Solid State Circuits 2018, 53, 2202–2213. [Google Scholar] [CrossRef]
- Askari, M.; Kaabi, H.; Kavian, Y.S.; Ajabi, S. A wideband 5-bit switched step attenuator in 0.18 µm CMOS technology. IETE J. Res. 2015, 62, 295–300. [Google Scholar] [CrossRef]
- Jarihani, A.E.; Kocer, F. A phase coherent 7-bit digital step attenuator on 0.18μm SOI. In Proceedings of the 2017 12th European Microwave Integrated Circuits Conference (EuMIC), Nuremberg, Germany, 8–10 October 2017; pp. 167–170. [Google Scholar] [CrossRef]
- Dogan, H.; Meyer, R.G.; Niknejad, A.M. Analysis and design of RF CMOS attenuators. IEEE J. Solid State Circuits 2008, 43, 2269–2283. [Google Scholar] [CrossRef]
- Ahn, M.; Kim, B.S.; Lee, C.; Laskar, J. A high power CMOS switch using substrate body switching in Multistack structure. IEEE Microw. Wirel. Compon. Lett. 2017, 17, 682–684. [Google Scholar] [CrossRef]
- Huang, Y.; Woo, W.; Yoon, Y.; Lee, C. Highly linear RF CMOS variable attenuators with adaptive body biasing. IEEE J. Solid State Circuits 2011, 46, 1023–1033. [Google Scholar] [CrossRef]














| Number of Row Vias. | Number of Column Vias | Parasitic Inductance (pH) | Parasitic Resistance (mΩ) |
|---|---|---|---|
| 1 | 3 | 33 | 37 |
| 2 | 2 | 28 | 26 |
| 1 | 7 | 23 | 17 |
| 1 | 12 | 17 | 9 |
| 2 | 7 | 15 | 10 |
| 2 | 5 | 11 | 5 |
| 2 | 12 | 8 | 5 |
| 2 | 22 | 6 | 3 |
| Atten. (dB) | Topology | Rs (Ω) | Ro (Ω) | Rp (Ω) | Rc (Ω) | W1,3,5 (μm) | W2,4,6,7 (μm) | Cc (fF) | Cp (fF) |
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | Bridge-T | 5.92 | 40.9 | 368 | 0 | 40 | 15 | 0 | 17 |
| 1 | Bridge-T | 15.7 | 74.1 | 1293 | 0 | 90 | 20 | 0 | 17 |
| 2 | Bridge-T | 20.7 | 164.6 | 873 | 0 | 80 | 20 | 0 | 83 |
| 4 | T-type | 15.3 | 0 | 90.5 | 0 | 80 | 15 | 0 | 50.7 |
| 8 | Pi-type | 0 | 0 | 91.1 | 53.7 | 60 | 15 | 84.2 | 58.1 |
| 16 | Pi-type | 0 | 0 | 50.1 | 70.6 | 20 | 15 | 102.5 | 152.2 |
| Reference | [12] 2017 | [13] 2017 | [16] 2016 | [17] 2018 | [18] 2010 | [21] 2018 | This Work |
|---|---|---|---|---|---|---|---|
| Frequency (GHz) | 19–21 | 14–18 | 6–12.5 | 20–24 | DC–14 | DC–20 | 12–17 |
| Technology | 0.18 μm CMOS | 0.35 μm BiCMOS | 0.25 μm BiCMOS | 0.13 μm BiCMOS | 0.18 μm CMOS | 0.13 μm BiCMOS | 0.13 μm BiCMOS |
| Number of Bits | 6 | 6 | 7 | 6 | 6 | 6 | 6 |
| Attenuation Rang (dB) | 32 | 31.5 | 16.51 | 31.5 | 31.5 | 31.5 | 31.87–30.31 |
| Attenuation Step (dB) | 0.5 | 0.5 | 0.26 | 0.5 | 0.5 | 0.5 | 0.5 |
| RL (dB) | >12 | >10 | >13 | >9 | >10 | >12 | >13 |
| IL (dB) | <8 | 8±0.6 | <12.7 | 20.9–21.95 | <10 | 1.7–7.2 | 6.99–9.33 |
| RMS Amplitude Error (dB) | N/A | <0.29 | <0.26 | <0.43 | <0.5 | <0.37 | 0.58–0.36 |
| RMS Phase Error (°) | <3.8 | <3.9 | 2.2–3.5 | 1.6–4.2 | <4.2 | <4 | 2.06–3.46 |
| IP−1dB (dBm) | N/A | 10 | 12.5 | 14 | 15 | 10 | 13.6–16.2 |
| Die area (mm2) | 0.451 | 0.271 | 0.291 | 0.772 | 0.51 | 0.982 | 0.92 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Li, Z.; Yao, Y.; Cheng, G. A 6-Bit Ku Band Digital Step Attenuator with Low Phase Variation in 0.13-μm SiGe BiCMOS. Electronics 2019, 8, 1149. https://doi.org/10.3390/electronics8101149
Luo L, Li Z, Yao Y, Cheng G. A 6-Bit Ku Band Digital Step Attenuator with Low Phase Variation in 0.13-μm SiGe BiCMOS. Electronics. 2019; 8(10):1149. https://doi.org/10.3390/electronics8101149
Chicago/Turabian StyleLuo, Lei, Zhiqun Li, Yan Yao, and Guoxiao Cheng. 2019. "A 6-Bit Ku Band Digital Step Attenuator with Low Phase Variation in 0.13-μm SiGe BiCMOS" Electronics 8, no. 10: 1149. https://doi.org/10.3390/electronics8101149
APA StyleLuo, L., Li, Z., Yao, Y., & Cheng, G. (2019). A 6-Bit Ku Band Digital Step Attenuator with Low Phase Variation in 0.13-μm SiGe BiCMOS. Electronics, 8(10), 1149. https://doi.org/10.3390/electronics8101149