Efficient Neural Network Implementations on Parallel Embedded Platforms Applied to Real-Time Torque-Vectoring Optimization Using Predictions for Multi-Motor Electric Vehicles

Abstract

The combination of machine learning and heterogeneous embedded platforms enables new potential for developing sophisticated control concepts which are applicable to the field of vehicle dynamics and ADAS. This interdisciplinary work provides enabler solutions -ultimately implementing fast predictions using neural networks (NNs) on field programmable gate arrays (FPGAs) and graphical processing units (GPUs)- while applying them to a challenging application: Torque Vectoring on a multi-electric-motor vehicle for enhanced vehicle dynamics. The foundation motivating this work is provided by discussing multiple domains of the technological context as well as the constraints related to the automotive field, which contrast with the attractiveness of exploiting the capabilities of new embedded platforms to apply advanced control algorithms for complex control problems. In this particular case we target enhanced vehicle dynamics on a multi-motor electric vehicle benefiting from the greater degrees of freedom and controllability offered by such powertrains. Considering the constraints of the application and the implications of the selected multivariable optimization challenge, we propose a NN to provide batch predictions for real-time optimization. This leads to the major contribution of this work: efficient NN implementations on two intrinsically parallel embedded platforms, a GPU and a FPGA, following an analysis of theoretical and practical implications of their different operating paradigms, in order to efficiently harness their computing potential while gaining insight into their peculiarities. The achieved results exceed the expectations and additionally provide a representative illustration of the strengths and weaknesses of each kind of platform. Consequently, having shown the applicability of the proposed solutions, this work contributes valuable enablers also for further developments following similar fundamental principles.

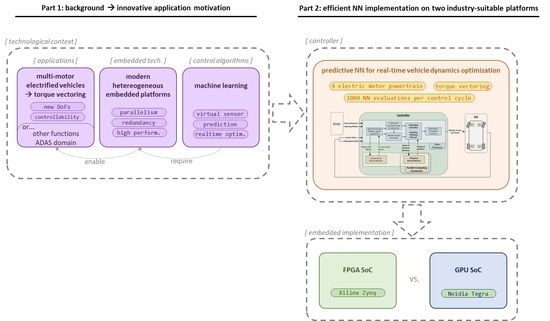
1. Introduction

As vehicle electrification moves forward [1,2], new powertrain topologies are appearing and attractive research and innovation opportunities for developing enhanced propulsion systems can be identified [3]. The potential of the increased degrees of freedom and controllability of powertrains driven by multiple electric motors can be unleashed by exploiting several enabler technologies which are addressed in this work, aiming to implement sophisticated Torque-Vectoring techniques [4,5,6]. Furthermore, this kind of advanced active chassis control systems not only can be eventually categorized inside the field of ADAS by themselves but they also can be exploited to support further ADAS -or even automated driving- functionalities, such as active support in critical evasive manoeuvres or to provide predictions and estimations of unmeasurable variables to take corresponding actions.

The cited applications imply multiple requirements which are satisfied by modern high performance heterogeneous embedded platforms. While keeping reasonable cost points and power consumption, they are bringing vast computing power and intrinsic parallelism (for performance) and redundancy (for safety). This power can be harnessed to implement complex algorithms, including Machine Learning, in both the cited application fields [7,8,9,10,11,12,13,14,15,16,17,18]. Furthermore, such advanced controller designs can be greatly supported by the means of the continuously improving model-based development solutions. However, major challenges appear not only on the notably complex technical layers but also in the regulatory layer addressing safety-critical applications [19,20].

This context has motivated the research presented in this work, in which after a deeper discussion about the abovementioned topics, we use Machine Learning to target a complex optimization problem—as are vehicle dynamics- in a typically constrictive domain—as are automotive systems-, thus providing an illustrative, innovative and challenging application. Specifically, this work leads to a detailed analysis of the embedded implementation of a conventional neural network (NN) aiming to rapidly provide batches of predictions within a real-time optimization algorithm. The representative use case consists in predicting the slip of the wheels for a batch of possible future control actions determined by a multi-objective Torque-Vectoring optimization algorithm. We have implemented the computationally demanding NN inference, which delivers batches with many evaluations per control cycle, on two different highly parallel platforms, aiming to evaluate their suitability and potential. The embedded platforms are a FPGA and a GPU, each integrated inside SoC devices with adequate industry suitability.

The remainder of the paper is structured as follows. Section 2 extends the key topics discussed in this introduction section, highlighting the most relevant aspects of the technological context which motivate and support this research, focusing particularly on the embedded platforms, as they are the keystone to enable the upcoming implementation work. Section 3 introduces the particular automotive control use case, targeted to illustrate the applicability of the proposed solution. Section 4 describes the proposed control solution, starting with an overview over the general approach, discussing relevant restrictions regarding automotive systems and finally introducing the NN itself. Section 5 and Section 6 carefully describe the implementation of the said NN inference, respectively using embedded GPU and FPGA components. After a brief introduction focusing on the different computation paradigms, implementation details are presented and discussed by means of theoretical discussion and intermediate results. Section 7 summarizes the final results, first regarding the prediction capability of the NN itself and then focusing on the embedded implementation. Finally, Section 8 and Section 9 summarize conclusions and future work respectively.

2. Technological Context

2.1. Heterogeneous Embedded Platforms

The field of embedded platforms has typically shown a steady evolution regarding computing power and features. But beyond that, recent years are showing an uprising variety of new solutions providing notable and attractive computing capabilities, as exemplified in Figure 1. This is fuelled not only by faster clock rates and multi-core designs—which are only providing a moderate performance growth rate- but also by the integration of different computing paradigms into heterogeneous embedded platforms which can act as accelerators for complex algorithms. This evolution has been strengthened by the fact that the application fields for platforms such as FPGAs and GPUs have been widened. The result is a remarkable leap forward regarding computing capacity powered by their vast intrinsic parallelism, with the potential of providing at least one order of magnitude gain with respect to conventional processor-based devices [7,21,22,23,24,25,26].

The remainder of this section provides an overview about the more relevant embedded platform types and the evolution of their topologies, emphasizing the trend towards heterogeneous devices and SoCs.

Microcontrollers keep enhancing their capabilities for hard real-time and safety critical applications by implementing redundant cores—i.e., lockstep- and diverse error protection mechanisms. Besides, they are also showing performance gains not only through higher clock frequencies and parallel cores but also offloading functions to dedicated hardware modules [27,28].

Application oriented microprocessors provide typically higher clock frequencies and more cores than microcontrollers, often even with notable 64 bit processing capabilities providing faster double precision floating point operations. They represent a powerful solution for a wide variety of demanding applications but unless combined with elaborate software solutions or some other elements—e.g., real-time co-processing cores and certain integrity mechanisms- their suitability for safety-critical real-time control functions is rather limited. Equally to the microcontrollers, their sequential code execution paradigm only is capable of providing limited parallelism [29,30].

FPGAs enable very fast cycle times and massive throughput due to their programmable hardware nature with intrinsic parallelism and pipelining, as better detailed in Section 6. As their performance figures grow at a remarkable rate and good capabilities are available even for cost-sensitive devices, their current and potential application fields are widening [7,21,22,24,26,31].

GPUs base their instruction execution paradigm on a massive multi-core architecture which also provides high intrinsic parallelism. They have evolved from graphical and multimedia applications to also tackle computing tasks in desktop environments, also propagating this trend to embedded devices. An in-depth discussion on these devices is given in Section 5 [7,9,10,25,32].

Finally, SoCs are bringing a new generation of heterogeneous devices to the market which offer different combinations of the abovementioned device types. Besides SoC approaches typically used in other domains such as multimedia consumer products, new computation and control oriented SoCs offer great improvements. Over one order of magnitude of performance gain can be expected by combining multi-core processors with at least one of the previously mentioned highly parallel GPU and FPGA computing solutions [21,22,23,24,25,33].

Figure 1 illustrates the mentioned variety of platform types, with representative examples focusing on the topology of the architectures. Additionally, some indicative GFLOP/s (giga floating point operations per second) values are given to illustrate the performance order of magnitude that can be expected. It is worth noting that these values are rough theoretical peak numbers and must not be misinterpreted: the effective performance figures depend greatly on both the application itself and its implementation, thus requiring exhaustive analysis for each case. Achieving maximum performance requires correctly exploiting the capacity of the instruction sets, caches, parallelism, different kinds of pipelining and so forth. Such complex implementation aspects are discussed in detail, for the selected FPGA and GPU platforms, in the upcoming Section 5 and Section 6 [26,34,35].

Furthermore, it must be noted that some of the highest performing devices are excessively costly to be considered suitable for the typical automotive price ranges. The highest performing microcontrollers and microprocessors might have a borderline reasonable cost point but currently only the SoCs on the lower performance end are considered to be suitable for the typical automotive cost constraints, although technology and the market keep improving the performance/cost ratios.

The computing power provided by the more powerful platforms previously discussed, enables implementing relatively complex and computationally demanding algorithms. A clear example is the currently very active domain of perception algorithms for ADAS and automated driving, with current research involving Machine Learning and Deep Neural Networks (DNNs) [7,8]. Similarly, this paper aims at benefiting from the discussed computation gains but for relatively smaller networks within more restrictive applications, as will be explained in Section 3.

2.2. Multi-Electric-Motor Powertrains

Electrified vehicles—i.e., hybrid and pure electric vehicles- are showing a steadily growing sales trend [1,2]. This is not only pushed by environmental and geo-political/economic considerations which have brought stringent regulations, related to emission issues [36] and even certain scandals [37]. It is also driven by improving acceptance rates as technology is evolving and providing better capabilities at more affordable prices [1,2]. Consequently, some electrified powertrain topologies are evolving towards multi-motor configurations which are beyond conventional hybrids typically equipped with just one motor of each kind. Such a topology is illustrated in Figure 2.

Powertrains with independent motors for each of the wheels on a same axis enable the implementation of refined Torque-Vectoring algorithms. Torque-Vectoring relies on controlling the torque of each wheel aiming not only to enhance cornering performance but also to enhance stability and consequently increasing safety [38,39], as will be further discussed in Section 3.

Although these new technologies are being introduced mostly in high-performance cars, they are expected to propagate to the mainstream sector, where they could provide the abovementioned technical benefits, besides enabling constructive advantages like better space utilization.

Table 1. Overview of some relevant multi-motor vehicles [3,40,41,42,43,44,45,46,47].

Powertrain Type	Hybrid FWD	Hybrid 4WD			Electric RWD	Full Elec. 4WD	Full Electric 4-Motor 4WD
Vehicle	Chevrolet Volt	Porsche 918	Honda-Accura NSX	Mercedes AMG Project One	BMW i3	Tesla P100D	Mercedes AMG SLS e-Drive	Rimac Concept One	NIO EP9
Highlights	Value	Perform.Innovat.	4 motors (incl. petrol)		Optional range extender	Range Accelerat.	4 independent electric motors; Handling by Torque Vectoring; Record-breaking performance
Motors	2 electric	2 electric (per axle) 1 petrol (rear axle)	3 electric (2 front, 1 rear) 1 petrol (rear)		1 electric 1 petrol	2 electric (per axle)	4 electric (per wheel)
Torque Vect.	✗	~ per axle	✓ front axle	✓ front axle	✗	✗	✓	✓	✓
Power	149 HP	887 HP	573 HP	~1200 HP	170 HP	525 HP	751 HP	1224 HP	1360 HP
Year (appear)	2015	2013	2016	2018	2014	2015	2013	2016	2016/TBD
Mass	1607 kg	1700 kg	1725 kg	TBD	1422 kg	~2200 kg	2110 kg	1900 kg	1735 kg
0–100 km/h	7.5 s	2.6 s	3.1 s	2.5 sec	7.0 s	2.5 s	3.9 s	2.5 s	2.7 s
Price	~34.000 $	~900.000 $	~150.000 $	TBD	~43.000 $	~140.000 $	~400.000 $	TBD	TBD

summarizes a selection of relevant electrified vehicles, either hybrid or full electric. It illustrates that beyond conventional hybrids, multi-motor powertrains are progressively appearing, most of them enabling the implementation of Torque-Vectoring on two or four wheels, which is the foundation of the presented use case.

2.3. Complexity, Safety Criticality and Regulations Concerning Automotive Control Systems

Relevant changes worth considering are occurring, besides the powertrain control domain, in the field of vehicle control systems in general. As the number of components and functions in modern vehicles increases, the complexity and its derived issues are reaching hardly sustainable levels, with up to over 100 million lines of source code distributed on board among over 100 ECUs (electronic control units). In this scenario, besides infotainment and comfort features, the advent of vehicles with multiple motors and energy sources, as well as ADAS and Automated Driving capabilities, are strongly contributing to the above mentioned complexity issue [48].

The technical challenges associated to the introduction of modern complex control systems are increased further by several industry-related constraints. Firstly, some well-known aspects inherent to the big-scale vehicle industry need to be considered, such as extreme cost sensitivity and diverse modularity requirements, all combined with accelerating product cycles [49]. Secondly, major restrictions have been added to this already challenging scenario, with the introduction of new standards and regulations addressing safety critical systems from the functional point of view. Standards—such as the recently updated ISO-26262 [50]- require costly and time-consuming tasks to be fulfilled for the certification process. This includes methodically addressing requirement traceability, validation and documentation and the need for exhaustive analysis like HARA (hazard analysis and risk assessment) and FMEA (failure mode effects analysis) [28,51].

In what respects to the software development, several enabler technologies can be highlighted to provide means to tackle some of the challenges associated to these points. From the software point of view, steadily advancing toolchains enable elaborate model-based development approaches to be applied, typically aligned with the V development methodology. This includes highly automated tools providing hardware abstraction through automatic code-generation—or hardware synthesis for FPGAs-, which can be helpful to tackle the complexity of modern embedded platforms and exploit the features of heterogeneous devices. It also includes tools for automated testing—from Model-in-the-Loop (MiL) to Hardware-in-the-Loop (HiL)- and also requirement management and documentation solutions. Consequently, besides providing means for agile, efficient and modular developments, they can also notably facilitate the required test and validation of complex algorithms, as the ones discussed in this work [6,51,52].

In what respects to the hardware, the embedded platforms discussed in the previous Section 2.1 also represent a set of enabler technologies with notable relevance by providing protection mechanisms, redundancy and diversity. Furthermore, the gains in computational power and the multicore and heterogeneous topologies, do enable a further solution: consolidating the control architecture by integrating multiple control units into one ECU [48,53].

3. Targeted Application: Quadruple Electric-Motor Vehicle

The bottom-line of the above discussed topics leads to the motivation already anticipated in the introduction: we aim to provide enabler solutions targeting advanced Torque-Vectoring algorithms with real-time optimization, which represent a challenging application and a restrictive domain. In particular, our research efforts were dedicated to assessing the usability of automotive-suitable parallel embedded platforms for deploying such advanced control algorithms on vehicles with up to four independent electric motors.

The controller we propose uses NNs to estimate unmeasurable vehicle dynamics signals, in this case the prediction of future values. Being the target signals in the future, their values depend on the different control actions that the Torque-Vectoring could apply, meaning that the effect of many possible control actions will have to be evaluated and optimized in real time. Details on the control algorithm will be disclosed in Section 4.

Firstly focusing on the vehicle itself, quadruple-electric-motor powertrains present several advantages from the control point of view. By having independent control over the torque applied to each of the four wheels, they allow the implementation of sophisticated control strategies, basing on the Torque-Vectoring approach previously mentioned also in Section 2.2 and Figure 2 [6,38,54]. In comparison to the hybrid topology illustrated in this figure, in the targeted vehicle there is no differential on the rear axis, thus, in the same way as on the front axis, the torque on each of the rear wheels can also be directly controlled. This further increases the degrees of freedom of the controller. Besides, electric motors offer better controllability than internal combustion engines—as they provide a faster and more precise torque delivery [4,5]-, which is another reason for aiming at a more refined controller with short control cycles.

From the vehicle dynamics point of view, having four independent motors enables ideal Torque-Vectoring capabilities. The principle of operation is the following: when driving in a curve, dynamic weight transfer occurs along the vehicle’s chassis, meaning that the wheels on the exterior side of the curve will temporarily support a greater normal force and provide greater traction capacity. This can be very conveniently exploited by reassigning a part of the torque from the interior wheels to the exterior ones. As has also already assessed by means of race-track tests in previous works [6,39,54,55], this does not only avoid the inner wheel to spin because of the lower traction capacity but it also generates an additional yaw moment, helping the vehicle rotate over its vertical axis towards the direction of the curve, thus mitigating understeer—i.e., the front wheels turning the car less than expected according to their steering angle- [38,56].

Besides the vehicle dynamics aspects, having four motors also provides enhancement potential regarding energy efficiency. This is due to the fact that each electric motor will have different degrees of efficiency depending on their operating point—i.e., current rotation speed and applied torque, as well as temperature-. Therefore, depending on the situation, a reassignment of the torque demand from one motor to another—i.e., a motor increasing its torque delivery with another being set to handle less power- could lead to a better global efficiency.

Furthermore, also thermal aspects are to be taken into account. Excessive temperatures on the motor components and power electronics must be avoided. As the motor loads will be unbalanced, so will the heat accumulation. This means that trying to re-balance the temperature distribution should be added as an extra aspect for the control function.

Finally, besides the handling, efficiency and thermal optimization, a fourth aspect to be considered is the smoothness of operation, aiming at improving stability and comfort, while reducing mechanical stress and wear on different components.

The aspects to be controlled that have been discussed in the previous paragraphs are illustrated in Figure 3 and represent a challenging multi-objective optimization problem which is addressed with an elaborate control solution, as described in the following Section 4.

4. Advanced Controller Design: NNs for Batch Prediction Based Real-Time Optimization

4.1. Description of the Control Problem

As described in the previous Section 3, the torque of four independent motors needs to be controlled in order to optimize not only the handling but also the efficiency, the thermal load and the smoothness of operation, all of which depends on different input variables. This means that it is not only a multi-objective optimization problem but also a MIMO (multiple input multiple output) system.

The 4 outputs of the system are the torque set points for each wheel ($T_{FL},T_{FR},T_{RL},T_{RR}$). However, one degree of freedom is reduced and the control variables reformulated from 4 to 3, by imposing their sum to equal the requested total torque set point ($T_{tot}$) according to the throttle command. A natural way to reformulate this problem from the automotive engineering perspective is to define the variables as follows:

$$\begin{array}{c}{T}_{FL}+T_{FR}+T_{RL}+T_{RR}=T_{tot}=\\ =\left(1-D_{long}\right)\left[\left(1-D_{front}\right)T_{tot}+D_{front}{T}_{tot}\right]\\ +D_{long}\left[\left(1-D_{rear}\right)T_{tot}+D_{rear}{T}_{tot}\right]\end{array}$$

(1)

being $D_{long}$ the longitudinal torque distribution along axes (% of torque to rear axis) and $D_{front}$ and $D_{rear}$ the lateral distribution among each of the axes.

Figure 4 provides a simplified overview of the controller-level diagram, highlighting in bold the parts of most relevance for this paper and marking with dashed lines the NN inference part that needs to be accelerated and on which the following sections will focus on.

In essence, the controller relies on a simpler Torque-Vectoring algorithm to determine the default torque distribution value. Then it applies a multi-objective optimization algorithm in order to find an optimized torque distribution in the surroundings of the default value.

It is worth noting that the multi-objective MIMO optimizing strategy dynamically adjusts the priorities of each of the objectives according to the situation in real-time, evaluating several inputs which provide information about the driving situation of the vehicle. Vehicle dynamics is generally the top priority objective, especially when the driving state is getting closer to critical limits. Otherwise, energy efficiency is kept predominant, unless temperatures get closer to the functional limits, which progressively increases the weight of the corresponding objective.

Vehicle dynamics are the most critical part from the safety point of view and they are also critical in what respects to their computation for an algorithm such as the one targeted in this work. Good evaluation functions for aspects concerning efficiency, temperature and comfort can be integrated in the controller with reasonable effort due to their nature. But the complex and strongly non-linear interactions of the many physical magnitudes and degrees of freedom involved in vehicle dynamics are notably more complicated to model and control [56,57].

This paper focuses on the technical challenge of predicting such magnitudes in real-time under the constraints of an automotive control system. A relevant reference point is that even running a single instance of a vehicle dynamics model is already a major challenge on an embedded platform [57]. It must be considered that the targeted application requires not one but a batch of evaluations of the vehicle dynamics -to predict the effect of the control actions for the optimizing algorithm- which we have determined in a typical range between several hundreds and a few thousands. In order to reduce the computational cost and make it possible to execute all the evaluations in the stringent time of a control cycle which has been specified with 5 ms, we chose a Machine Learning approach as prediction solution. In particular, we selected a NN, which is further described in Section 4.3.

The targeted use case in this paper is the estimation of future slip values of each wheel for a batch of possible Torque-Vectoring set points. These predictions are used to select the torque distribution that will reduce unnecessary slip, while also satisfying the efficiency, thermal load and the additional smoothness criteria. In order to achieve good predictions, a careful selection of the relevant input signals is necessary, which was based on a combination of expert knowledge in the field of vehicle dynamics and evaluation of the outcome of different input sets. The signals firstly need to include the torque set points for each wheel, as it is their effect to be evaluated. The remaining signals are related to the current state of the vehicle and therefore are equal for all the potential solutions. These include, the current wheel slips, the steering wheel position, inertial sensor (accelerations and angular velocity on 3 axes) and vehicle speed, adding up to 16 inputs. Additionally, an extended input set of 24 is also evaluated, including derivatives of the inertial sensor and two metrics of theoretical nature related to the steering wheel and vehicle speed. These are meant to reflect the transient behaviour of the involved dynamics over time.

4.2. Restrictions of Automotive Systems

One notable characteristic of automotive control systems is their series of relatively stringent constraints, as already anticipated in Section 2. On the side of the embedded electronics there are the requirements affecting their cost and features and consequently their performance. This means that the algorithm should be as computationally efficient as possible. But significant restrictions are also to be considered in what respects to the functionality, especially for safety-critical control functions—as is the case for powertrain applications like the one presented- which are addressed by regulations like the ISO-26262 and the corresponding certification implications [28,51,52].

The control architecture and the individual sub-functions have been carefully conceived to reduce the degree of uncertainty, facilitate its mathematical analysis and mitigate the impact of an eventual prediction malfunction. This inevitably induces the control algorithm and the predictive and virtual sensing algorithms to be designed avoiding unnecessary complexity, not only to enhance computational efficiency but also to enhance robustness and furthermore facilitate the analysis of its intended behaviour. In this sense, a relatively simple NN architecture is preferred, which additionally reduces computational cost.

Another fundamental consideration to be highlighted is that the malfunction of a virtual sensor should be considered similarly to a malfunction of a physical sensor, as both can potentially suffer some kind of error and need the corresponding support mechanisms to mitigate the effect.

The final consideration is that the designed optimizing algorithm is conceived to provide an enhanced set-point over the default Torque-Vectoring algorithm, aiming to reduce the slip but it must not be permitted to cause critical situations. It might happen that anyway certain slip occurs, in the same way slip can happen with a generic Torque-Vectoring or simply a normal torque distribution. The worst case scenario would be some other unwanted effect which could eventually affect the stability of the vehicle. But in such an unlikely situation, a superior layer of conventional traction and stability control functions—i.e., TCS and ESP- can override the torque set-points.

To mitigate the risk of stability systems having to intervene in such a worst case scenario, a series of additional pre-emptive mechanisms have been put in place in order to enhance the robustness and stability both of the estimations and the control actions. These include simple elements such as saturators and rate-limiters but also more elaborate functions that detect excessive fluctuations in multiple time windows. Furthermore, a simplified mathematical model is used to enable plausibility checks. Whenever unexpected values are detected, logical functions trigger an error and smoothly fall back to the default Torque-Vectoring values.

4.3. Definition of the Algorithm: A Neural Network

The remainder of this work focuses on the NN in particular and its implementation on the two selected embedded platforms. We chose a relatively simple Feedforward NN algorithm for a variety of reasons, having also considered other plausible approaches for a system with a dynamic time behaviour as the one described, like for instance Recurrent Neural Networks (RNN) [58,59,60] or Long Short Term Memory (LSTM) Networks [61,62,63], as well as solutions involving Kalman Filter based approaches [64,65,66]. Considering that a review over the broad diversity of possible solutions or even a more detailed comparison with respect to the ones just mentioned, cannot be covered in the scope of this paper, it is still worth noting some relevant points which have supported the selected option. The fundamental reason is that the performance of this simpler NN can be considered as adequate regarding the accuracy and tolerances for this controller, as will be seen in the results in Section 7. Furthermore, in general terms, the simplest possible design is preferred for the sake of reducing complexity in what refers to computation -for speed- as well as in what refers to the analysis of the NNs behaviour -for robustness and regulations-, as already discussed in the previous sections. Furthermore, information about the variation in time of signals for which this information is relevant can be included into to NN by the means of feeding filtered derivatives of those signals into its inputs. Furthermore, this approach simplifies the layered kernel approach on the GPU, as well as the hardware implementation on the FPGA. In fact, the very same logical blocks that are used in the FPGA for the batch predictions, can easily also be used for simpler virtual sensing purposes, which is convenient to save programmable area and associated costs.

This section describes briefly the fundamentals of the proposed NN archetype, the Multilayer Perceptron [67,68], for the purpose of setting a common ground for the upcoming platform dependent implementation discussions (Section 5 and Section 6).

As illustrated in the flow chart in Figure 5, once the input signals are received, they need to be scaled to normalized values, before the execution of the actual NN can start with the hidden layers. For each hidden layer, each of its neurons needs to apply a weight to each of the signals from the previous layer (or the inputs, in the case of the first layer) and calculate the resulting sum. This can be represented as a multiplication of a vector with a matrix and can be also implemented as dot products. Having the intermediate results of the previous layer, the bias values are added to each output. The final output of the layer is obtained after applying the activation function for each neuron. This process is repeated for each hidden layer, until reaching the output layer. This last layer does not have an activation function and will provide the results to be scaled to get the actual NN outputs.

It is relevant to understand that due to the vectorial and matrixial character of the operations, the computational complexity and spatial complexity are not neglectable. The dimensions are represented as $L_0$ for the amount of inputs and $O$ for the output count. Each hidden layer numbered from $1$ to $H$ with the index i, has $L_i$ neurons, meaning that the dimension of the weight matrix will be $L_{i}x{L}_{i-1}$ and the bias vector $L_i$. Consequently, the count of parameters (weights and biases) and basic math operations are expressed in (2) and (3) respectively.

$$N{N}_{Params}=2L_0+{\displaystyle \sum _{i=1}^H}\left(L_i\left(L_{i-1}+1\right)\right)+O\left(L_H+3\right)$$

(2)

$$N{N}_{Opers}=2L_0+{\displaystyle \sum _{i=1}^H}\left(L_i\left(2L_{i-1}+1\right)\right)+O\left(2L_H+3\right)$$

(3)

The mathematical operations from (3) are decomposed in multiplications and additions in (4) and (5).

$$N{N}_{MultOpers}=L_0+{\displaystyle \sum _{i=1}^H}{L}_i{L}_{i-1}+O\left(L_H+1\right)$$

(4)

$$N{N}_{AddOpers}=L_0+{\displaystyle \sum _{i=1}^H}\left(L_i\left(L_{i-1}+1\right)\right)+O\left(L_H+2\right)$$

(5)

To the previous basic arithmetic operations, the operations for the computation of the activation function needs to be added. As each hidden neuron includes an activation function, the number of activation functions equals the number of hidden neurons, as in (6).

$$N{N}_{hidden\_neurons}={\displaystyle \sum _{i=1}^H}\left(L_i\right)$$

(6)

In this work a NN with a sigmoidal activation function, has been selected, expressed as in (7).

$$\mathrm{Sigmoid}\left(\mathrm{x}\right)=\frac{2}{1+e^{-2x}}$$

(7)

Besides increasing both the addition and multiplication count by one per hidden neuron, the reciprocal division and especially the exponential function can represent a notable computation cost, depending on the platform and the implementation. To tackle this issue, an approximate function could be implemented by the means of a look-up table (LUT) with a specific amount of data points. Therefore these operations are counted separately.

The following

Table 2. This theoretical values of complexity for different neural network topologies.

Topology						Complexity
In (L0)	Hidden Layers				Out (O)	Parameters	Operations	Activation Func. (Hidden Neurons)
	L1	L2	L3	L4
16	32	16	8	0	4	1284	2468	56
24	32	16	8	0	4	1556 (+21%)	2996 (+21%)	56 (+0%)
8	16	12	8	0	4	512 (−60%)	960 (−61%)	36 (−36%)
32	32	16	8	0	4	1828 (+42%)	3524 (+43%)	56 (+0%)
32	32	24	0	0	4	2020 (+57%)	3908 (+58%)	56 (+0%)
32	64	32	16	0	4	4860 (+279%)	9532 (+286%)	112 (+100%)
32	128	32	16	0	4	9020 (+602%)	17,788 (+602%)	176 (+214%)
32	64	64	32	16	4	9020 (+602%)	17,788 (+602%)	176 (+214%)

collects the theoretical complexity magnitudes—parameter and operation counts- for a few representative NN topology examples. A NN with three hidden layers $L_{1-3}$ of 32, 16 and 8 neurons respectively with a reduced input set $In$ of 16 is taken as default topology for the targeted use case. As for all other cases, the output count $Out$ is 4—one per wheel-, thus the topology is {16, 32|16|8, 4}. This is also taken as baseline to normalize relative complexity for other topologies. The same topology with an extended input set of 24 is also considered in the second row. The third row reflects a smaller topology which will be discussed during the FPGA development in Section 6. The remaining rows show examples for bigger topologies which might be of interest for other applications, illustrating the notable growth of complexity and the fact that even for the same quantity of neurons, these magnitudes change depending on the distribution across layers.

The impact of the scaling operations is almost negligible, accounting for $L_0+O$ multiply and addition operations (e.g., just 40 operations for the baseline NN). Furthermore, as these can be optimized by implementing them in the interfacing functions instead of repeating them for each NN, they are not included in our performance metrics. Similarly, as the presented work focuses on the computation and memory aspects of the GPU and FPGA implementations—and being the data transfer for the presented use case relatively small- the application and platform dependent overhead related to the different interfacing aspects are not accounted in this work.

5. GPU Implementation of Neural Network

GPUs are highly parallel instruction-based platforms which can be seen as a vastly extended multi-core processor but with a different architecture and instruction set. Historically developed for massive parallel manipulation of tasks related to computer graphics -such as pixel manipulation, three-dimensional graphics or filtering-, their architecture has been specifically optimized for high performance data-parallel workloads. After the advent of the programmable pipeline, usage of GPUs for general purpose applications affirmed as an active research field [69,70,71]. Furthermore, recognizing and exploiting synergistically the potential of both CPU and GPU architectures—e.g. in SoC devices- has showed to deliver even further computational gains [72,73].

The computational power and parallelism of GPUs has already been largely adopted for training DNNs, mainly targeting computer vision and other machine learning applications [8,9,10]. Besides, GPUs demonstrated to excel also for deployment of DNNs, with several tools arising for tackling the DNN inference challenge within dedicated embedded platforms [11,74].

For the developments presented along this paper, we exploit CUDA, a parallel computing platform and programming model created by NVIDIA [75]. In this environment and as is illustrated in Figure 6, heterogeneous programming is performed by having one host processor in charge of launching the execution of the parallel workloads on the GPU. Each program executed on the GPU is referred to as a kernel. Parallel execution of all threads in a kernel is structured as a grid of blocks, each block containing several threads, which are actually synchronously executed in several smaller sets called warps. Memory and communication among all the threads of a kernel are also structured following the same hierarchy (illustrated on the right side of Figure 6). Each thread has exclusive access to its registers but it is able to share its registers within all the threads of the same warp by means of shuffle operations. Within each block, threads can exchange information via shared memory, whereas the much slower global memory must be used for the wider scope of the grid level [75].

In this programming model, execution of the blocks is hardware dependent, with a block being allocated for execution on a given Streaming Multiprocessor (SM), as soon as its resource demand is satisfied. Therefore, the performance of such CUDA accelerated programs is strongly platform dependent.

For the sake of this work, we selected the affordable NVidia Tegra K1 SoC platform. The Tegra K1 features a GK20a GPU (Kepler architecture), including 192 SM3.2 CUDA cores clocked up to 852 MHz. The SoC is complemented with 4 ARM Cortex-A15 cores (ARMv7-A architecture) clocked at 2.0 GHz and an additional low power core at 1 GHz. It supports up to 8GB of (LP)DDR3 RAM. The warp size for the current architecture is fixed at 32, meaning that a program needs to have at least 12 warps running in order to theoretically maximize occupancy [25].

The remainder of the section describes the GPU implementation of the NN inference algorithm described in Section 4.3, focusing on the most important aspects necessary to unleash the full potential of the selected platform.

5.1. Multi-Kernel NN Inference

As a first step, we programmed—in C language- a single-thread CPU implementation of the NN inference algorithm described in 4.3 and then migrated it to GPU by means of CUDA. As depicted in Figure 7, the NN inference implies a sequence of different parallelizable tasks. Besides the values propagated between tasks, reading of constant parameters is also necessary for weights and biases (blocks to the left in Figure 7).

The simplest implementation, referred as GM1, relies on Global Memory for both storage requirements. The size of the kernel launches -expressed in braces in the Figure 7 and given in

Table 3. NN inference on GPU: GM1 performance for batch of 512 NNs with {16, 32|16|8, 4} topology.

Layer	Kernel Size {grid a, block b}	Occupancy Achieved (Theoretical) [%]	Registers per Thread	Comput. Time [µs]
L1	{512, 32}	24.1 (25)	34	0.160
L2	{512, 16}	24.2 (25)	37	0.174
L3	{512, 8}	23.6 (25)	34	0.104
O	{512; 4}	22.7 (25)	21	0.061
Total				0.499

^a Number of thread blocks executed; ^b Number of threads per block.

- was set to be equal to the output layer dimensions. In GM1, each layer is implemented as an individual kernel launch. The profiling results -corresponding to the computation of a set of 512 NNs- confirmed the potential of using GPUs for NN evaluation, with a substantial speed-up of around 27x, w.r.t. the CPU performance, while also highlighting two main drawbacks: a suboptimal occupancy due to the chosen kernel sizes and a massive use of memory (and in particular of the texture units, needed for caching the reading operations).

We achieved a slightly better implementation, GM2, by tuning the kernel launch sizes, such to have larger thread blocks, each of them working on a fixed amount of NNs. The proposed modification resulted in a better usage of the GPU (higher occupancies), which is also reflected in a performance gain of a factor ~2x w.r.t. GM1. However, both GM1 and GM2 implementations share the drawback of abusing global memory for storing the intermediate data of the hidden layers -as depicted in Figure 7- and for reading the parameters -weights and offset values-.

5.2. Single-Kernel NN Inference: Shared and Global Memory

As a second step we developed the enhanced implementations -SM1 and SM2- by introducing the use of shared memory. We derived SM1 from GM2, using the same work partition strategy among the thread. However, we implemented the algorithm as a single kernel launch in order to enable the usage of shared memory for storing intermediate results between layers, thus avoiding the high latency corresponding to read/store operations from global memory. As shown in

Table 4. Inference on GPU: GM2, SM1, SM2 and CM implementations for a batch of 512 NNs with a {16, 32|16|8, 4} topology.

	Occupancy Achieved (Theoretical) [%]	Shared Memory (per Block)	Registers (per Thread)	Comput. Time [µs]
GM2-L1 a	53.6 (62.5)	0 B	43	0.090
GM2-L2 a	60.1 (75)	0 B	37	0.099
GM2-L3 a	60.5 (75)	0 B	33	0.033
GM2-O a	76.8 (100)	0 B	21	0.006
GM2-Total	58.65 (71.69) b	0 B	38 b	0.237
SM1 a	26.7 (31.2)	9 KiB	50	0.089
SM2 a	46.6 (50.0)	4 KiB	52	0.064
CM c	24.9 (56.2)	0 B	52	0.052

^a Kernel Size: 16 blocks, each block of 128 threads; ^b Values normalized w.r.t overall duration; ^c Kernel Size: 4 blocks, each block of 128 threads.

, the transition to shared memory provided an additional performance gain of about ~3x. However, it also resulted in reduced occupancy levels, because the limited amount of shared memory of each SM (configured as 48 KB for the used Kepler architecture) became the limiting factor, with a total of maximum 5 (rounding down 48/9) blocks per SM active, instead of the maximum of 16 allowed by the GPU.

Therefore, we pursued a more efficient usage of shared memory in SM2. This was achieved by buffering the storage and reading to shared memory in order to reuse the same buffer among the different layers. As reported in Table 4, SM2 offers a substantial performance gain of ~1.5x w.r.t. SM1, in line with the increased occupancy of ~1.75x and the increased complexity added to prevent race conditions.

5.3. Single-Kernel NN Inference: Registers + Constant Memory

In spite the notable net improvement w.r.t the CPU implementation, all the aforementioned implementations share the common bottleneck of reading the NN parameters (i.e., weights and bias of each layer) from global memory. As depicted in Figure 8, this resulted in overloading the texture memory buffer, with only marginal improvement achieved by the shared memory implementations.

The only feasible alternative for reading the constant values of the NN, is to exploit the GPU constant memory, which corresponds to a portion of the device memory accessed through constant cache. However, high reading performances from the constant memory are achieved only when all the threads access the same address simultaneously, in opposite to the concept of coalescent access pattern required for shared and global memory.

To enable an effective use of constant memory, we implemented the algorithm illustrated in Figure 7 to dedicate each thread to the evaluation of a different NN, thus allowing the required perfectly coordinated access to constant memory. Moreover, being the data flow of each thread independent from the others, storage of the intermediate results was implemented on the local scope of each thread, avoiding the need of shared memory and the corresponding synchronization mechanisms required for preventing race conditions.

The resulting final implementation (referred as CM) achieved the best GPU performances, with an incremental performance up to ~3x w.r.t the SM2 and an overall acceleration relative to a basic single-thread CPU implementation, ranging between ~68x and ~730x depending on the batch size, as showed in Figure 9. It can be observed how the batch size required to saturate the GPU depends on the implementation: while the computation time gains per NN for previous implementations saturate for batches beyond 256 or 512, the CM implementation takes 28 ns for 1024 evaluations, 20 ns for 4096 evaluations and as little as 18 ns for a batch of 8192 evaluations. Nevertheless, in spite of this remarkable maximum performance, it does not pay off for smaller batches, where the SM1 and SM2 implementations are faster.

This can be explained considering the theoretical occupancy of the CM version kernel. In fact, requiring 52 registers per thread (Table 4) and being launched in blocks of 128 threads, the GPU of the TK1 is saturated only when more than 9 blocks per SM are launched, which corresponds to a total of over 1152. Below that size, the size of the batch problem is not sufficient to compensate the latency of the required operations.

Additionally, the extended version of this NN with 24 inputs was also implemented. The computation time results of this are collected in Section 7.

6. FPGA Implementation of NN

FPGAs are versatile prefabricated silicon devices fundamentally consisting of generic logic cells, non-volatile embedded memory, digital signal processing blocks, input/output blocks and an interconnect structure. Basic FPGA structure is illustrated in Figure 10. Historically FPGAs arose as an alternative to ASICs (application specific integrated circuits) due to lower development and time-to-market expenses provided by their programmable character. Although, when compared to ASICs, FPGAs provide poorer cost/area, delay and consumption metrics, their flexible nature and performance turn them into convenient high performance devices for a diversity of solutions, especially in the field of signal processing applications with a relatively high throughput [76,77].

Internally, FPGA logic cells consist of a programmable combinational logic which feeds into fixed sequential logic in the form of D-type flip-flops (registers). This enables to pipeline a massive amount of data and to achieve parallel execution of algorithms. The principle of pipelining is illustrated in Figure 11. Essentially, in a fully pipelined solution, all functions (represented by the letter “F”) of the algorithm are executed concurrently and a new output is produced on every clock cycle once the latency time—needed for the signals of the first instance to propagate through the system- has passed [76,78].

Additionally, most modern FPGAs include DSP blocks, which usually ingrain multipliers and accumulators while improving power efficiency, chip size and timing for mathematical operations.

Regarding memory, embedded memory can be used as read-only-memory to store essential data but it can also be used for buffering. Memory is organized in blocks, which enable to use separate interfaces, meaning that they can be accessed concurrently [76,78].

The rise of more demanding algorithms—such as DNNs used for perception- is finding support in new features that vendors are introducing to FPGAs. For the implementation of algorithms using floating point variables on FPGAs, the usage of DSP blocks [7,79] and the reduction of numerical precision [80] are common solutions for the sake of performance and hardware resource efficiency.

Considerable research effort has been documented about NN implementations on FPGAs. Most of them focuses on convolutional NNs [12,13,14,15], whereas fewer works target smaller—or very small- feed-forward NNs [16,17,18]. Usually, the activation function of the NN is approximated using piece-wise-linear approximation or a LUT. Furthermore, for the sake of resource efficiency, floating point data is usually replaced with fixed point variables, thus reducing dynamic range [76,78].

For the sake of this work, we selected a Xilinx Zynq 7020 SoC platform. The Zynq 7020 features an Artix-7 FPGA combined with 2 ARM Cortex-A9 cores (ARMv7-A architecture) clocked at 666 MHz. The FPGA has 280 embedded memory blocks (4.9 Mb), 220 DSPs, 53200 LUTs (combinational logic) and 106400 registers (sequential logic). The processing system (ARM) and the FPGA are connected through multiple bidirectional interfaces, including support for direct memory access (DMA) and coherent and noncoherent access [24].

Although abstract schematics can be described effectively with hardware description languages such as VHDL and Verilog, this makes the implementations strongly hardware-specific thus limiting description reusability and maintainability. In view of a more solid applicability in the automotive industrial context, this work exploits Xilinx SDx tools, a modern High Level Synthesis (HLS) solution provided by Xilinx in combination with its Software-Defined SoC workflow [81]. This toolchain addresses the SoC design in general, as it provides the connection between hardware accelerator and processor software while the HLS tools allows HDL and Verilog code generation from C or C++ code properly enriched with a set of certain directives.

The remainder of this section describes the implications and challenges faced to achieve an optimized NN implementation on the FPGA fabric.

6.1. Automatic Hardware Synthesis of NN Inference

We implemented the NN inference algorithms for the FPGA as a C++ object in accordance with the description in Section 4.3. Vivado HLS synthesizes this C++ code into RTL (register transfer level) description. The RTL generation flow is tuned by means of special directives to manage implementation aspects such as pipelining, loop unrolling, array instantiation and port specifications.

The generated hardware accelerator design is passed to the Xilinx SDSoC (Software Defined System on Chip) tool, which enables to select intercommunication interfaces, create the software layer and implement the data mover between the processor and the FPGA.

In this work, we used the FPGA master communications model, where data transactions are conducted by the FPGA master. The overall implementation architecture is shown in Figure 12. The Data Mover is implemented as DMA (direct memory access) controller, connecting the FIFO based accelerator interface with the ACP (accelerator coherency port) of the processor, thus supporting cache coherent transactions.

As the FPGA part of the Zynq does not include dedicated floating-point arithmetic, these operations need to be implemented with the available resources. This requires a series of compromise solutions depending on the resource usage of different implementations, which we had to bring into consideration using different data types and precisions for the sake of reducing resource usage and increasing speed.

6.2. Theoretical Performance and Resource Utilization

FPGAs excel at performance when a fully pipelined implementation is achieved, as previously discussed and illustrated in Figure 11. When fully pipelined and if data is continuously fed, a new output result -or results- will be generated at every clock cycle after the latency time has elapsed. For instance, in a fully pipelined solution with a latency of 1000 ns at 100 MHz, the first output would be available after this 1000 ns latency time but consecutive outputs would be available every 10 ns.

Following (3–7) the total count of mathematical operations is determined. These operations are implemented using deterministic functional blocks, thus it is possible to theoretically determine the resource utilization of a NN.

Table 5. Resource utilization of single precision operations on Xilinx Zynq FPGA.

Instance	Resources
	DSP	Registers	LUTs
Multiplier	3	143	321
Adder	2	205	390
Divider	0	761	944
Exponent	7	277	924

illustrates the amount of resources each mathematical operation requires for single precision data type when selecting implementations which exploit maximum hardware DSP block utilization [82].

It must be noted that associating the total number of operations directly to the resource utilization corresponds to a fully pipelined implementation, which would provide a very fast throughput. This level of performance is determined to be above needed specifications and it would require excessive resources. By avoiding full pipelining, resource utilization can be reduced at the price of compromising speed. Nevertheless, for the following analysis, a smaller NN will be assumed, with a topology of {8, 16|12|8, 4}. Although this will still be too big for a fully pipelined implementation, it is adequate for different solutions of non-pipelined implementations.

Table 6. NN inference on FPGA: fully pipelined solutions for {8, 16|12|8, 4} topology.

Solution for NN	Resource Utilization								Latency [µs]
	BRAM		DSP		Registers		LUTs
	Total	%	Total	%	Total	%	Total	%
Single (theor.)	0	0.0%	2744	1247.3%	213,180	200.4%	425,412	799.6%	-
Single (HLS)	0	0.0%	2744	1247.3%	233,367	219.3%	427,469	803.5%	218
Fixed < 32 > (HLS)	0	0.0%	1148	521.8%	140,541	132.1%	216,208	406.4%	181
Fixed < 16 > (HLS)	0	0.0%	618	280.9%	73,890	69.4%	117,279	220.4%	134

illustrates the theoretical amount of resources a fully pipelined implementation of this NN requires, indicating the percentage of available resources in relation to the Artix-7 FPGA which is integrated in the Zynq 7020. The table also shows the real values achieved through the synthesized HLS implementation. Furthermore, the resource utilization of HLS implementations of 32 bit and 16 bit fixed point versions is also provided, although in this case the theoretical calculation is not straight-forward due to low-level aspects such as bit-level optimizations.

The obtained numbers confirm that a fully pipelined implementation would still require far more hardware resources than the selected Zynq 7020 has available. Roughly 12x the available DSPs would be needed for the single precision version. For the 16 bit fixed point version this is reduced to roughly 3x available DSPs. Consequently, the implemented solution described in the following section is a compromise solution.

6.3. Resulting Hardware-based NN Inference

We have tried different NN implementation approaches, both regarding data type as well as regarding the usage of LUTs, as summed up in

Table 7. NN inference on FPGA: implemented solution results for {8, 16|12|8, 4} topology.

Data Type	LUT	Resource Utilization								Normaliz. Mean Error	Computation Time [µs]
		BRAM		DSP		Registers		LUTs
		Tot.	%	Tot.	%	Tot.	%	Tot.	%
Single	No	0	0%	129	58%	23,919	22%	19,893	37%	~0%	5.53
Single	256	29	20%	98	44%	26,246	24%	21,782	40%	0.86%	4.92
Single	512	30	21%	98	44%	26,246	24%	21,873	41%	0.45%	5.04
Single	1024	30	21%	98	44%	26,246	24%	21,956	41%	0.29%	5.16
Fix32	No	0	0%	197	89%	23,051	21%	20,710	38%	0.04%	3.8
Fix32	256	27	19%	176	80%	18,739	17%	15,442	29%	0.89%	3.12
Fix32	512	27	19%	176	80%	18,739	17%	15,514	29%	0.46%	3.19
Fix32	1024	27	19%	176	80%	18,740	17%	15,738	29%	0.30%	3.25
Fix16	No	0	0%	86	39%	17,081	16%	16,867	31%	8.77%	2.02

. LUTs of different data point count are used to replace the costly mathematical functions for the sigmoid of the activation function as in (4). This is meant to reduce resource usage -mostly regarding DSPs- and accelerate the computation but it must be noted that they cannot be pipelined.

Regarding constant data handling, we implemented weights and biases using registers, in order to improve their access speeds.

The results illustrate that using LUTs accelerates the calculation and reduces the DSP usage, in exchange of using BRAM and some more registers and LUTs. The use of fixed-point data types reduces resource utilization, which permits to implement a faster solution, with more loop unrolling, which ultimately does consume more DSPs. Finally, the 16-bit precision solution outperforms the other solutions even without any loop unrolling, thus notably decreasing resource utilization but at the expense of excessive numerical error for the case of this implementation. Nevertheless, it must be noted that the error metrics should only be interpreted as indicative, as they would require further analysis, implementation optimization and training specifically for the specific data type.

As the previous intermediate results with the small NN have shown that acceptable performance and resource utilization can be achieved with fixed point data types, the originally targeted NN size is implemented for the 32 bit fixed-point implementation with the biggest LUT. The results for both 16 and 24 inputs versions are shown in

Table 8. NN inference on FPGA: implemented solution results for a batch of 1024 NNs {16, 32|16|8, 4} and {24, 32|16|8, 4} topologies with 32 bit fixed point and 1024 value LUT solution.

NN Topology	Resource Utilization								Normalized Mean Error	Average Computation Time per NN [µs]
	BRAM		DSP		Registers		LUTs
	Tot.	%	Tot.	%	Tot.	%	Tot.	%
16, 32|16|8, 4	52	37.%	184	83%	27,129	25%	40,787	76%	0.302%	4.20
24, 32|16|8, 4	56	40%	184	83%	30,872	29%	50,769	95%	0.318%	5.40

.

It must be noted that although avoiding the floating data type is a reasonable compromise which provides adequate results, it is expected that this compromise will eventually be less relevant in future FPGAs, as models with dedicated floating point functions are starting to appear even for low range families [83].

7. Results

Before proceeding to the core challenge discussed in this paper -which is the efficient implementation of the NN inference on the two automotive-suitable embedded platforms- Figure 13 shows the worst case prediction capabilities for the two selected NN topologies implemented in the targeted use cases: {16, 32|16|8, 4} and {24, 32|16|8, 4}. This particular plot is considered as worst case for two main reasons. Firstly, because with 50 ms it is providing a longer prediction horizon than really necessary. Secondly, because it is an extract of the most unfavourable situation among over 10 min of driving, subject to exceptionally strong fluctuations which result in notably worse accuracy and the appearance of a shift of up to roughly 15–20 ms.

The bottom-line is that the achieved accuracy of the predictions is certainly satisfying and adequate for the application, with a mean average error (over the entire lap) of just 0.28% and 0.24% for the NNs with 16 and 24 inputs respectively. For the especially difficult to predict situation illustrated in Figure 13, the values rise to 0.70% and 0.45% respectively. This illustrates that the NN provides sufficient capacity to adapt also to highly dynamic situations, including those of which only few fragments are present in the training dataset. It also shows the benefit of the extended inputs providing information about the derivatives of relevant signals.

Furthermore, several aspects must be emphasized in this respect. First, that the slip is strongly affected by random irregularities of the road surface, which are unknown and cannot be predicted. Second, that for the presented use-case, considering the lower time constant of the electric motors and the design of the presented Torque-Vectoring optimizing controller, the prediction can be adjusted to less challenging horizons under 50ms. Third, the said controller has been designed with far greater safety margins than the obtained accuracy, even for the worst case fragments.

In what respects to the setup and approach for the training and validation of these NNs, we generated a broad and diverse dataset, aiming to avoid overfitting and ensure good generalization, including a variety of road/track models (Nürburgring, Inta and different generic test tracks) and different driving styles (normal, aggressive, borderline and drifting) by different drivers. For this we relied on a high-fidelity multibody vehicle dynamics simulator (Dynacar, [84,85], also involved in real circuit tests in previous work for validation purposes [54,84]) integrated into an elaborate model-based development framework (using MatLab-Simulink for accelerated MiL tests as well as HiL validation [6,86]), together with models of other relevant components, subsystems and control units. Therefore, validation tests were performed using data generated by the same setup but driving differently. In particular, the final results were generated by one lap of mixed-style driving, including extreme manoeuvres on the Nürburgring, driving in opposite direction to the training data.

In conclusion this approach is highly representative to assess realistically the good learning and prediction capacity of the NNs and the outcome was successful even under the most challenging situations in what respects to dynamical behaviour of the predicted variables.

Ultimately focusing on the principal technical challenge which is addressed in the implementation part of this paper,

Table 9. Final summary of inference on GPU and FPGA for a batch of 1024 NNs with different NN topologies (selected solutions in bold).

Device	Implementation	Computation Time per NN [µs]
		NN Topology
	in: hidden: out:	{8, 16|12|8, 4}	{16, 32|16|8, 4}	{24, 32|16|8, 4}
GPU	GM1	-	0.509	0.567
GPU	GM2	-	0.232	0.264
GPU	SM1	-	0.077	0.087
GPU	SM2	-	0.058	0.071
GPU	CM	-	0.028	0.040
FPGA	Single (LUT-no)	5.534	-	-
FPGA	Single (LUT-1024)	5.092	-	-
FPGA	Fix32 (LUT-no)	3.832	-	-
FPGA	Fix32 (LUT-1024)	3.254	4.201	5.403
FPGA	Fix16 (LUT-no)	2.021	-	-

provides a wrap-up of the intermediate results together with the final results for the embedded NN implementation on the two selected embedded devices, the GPU and the FPGA.

The execution time results show the remarkable computation capacity of the selected embedded GPU SoC, providing an average computation time of just 40 ns per NN for a batch of 1024 evaluations of the targeted NN with extended inputs and even below 20 ns for bigger batches with 16 inputs.

In contrast, the performance of the FPGA has suffered from the notable penalty of not being able to implement a fully pipelined solution, providing an average computation time per NN of 5.4 µs for the extended inputs topology, which is 135x slower than the GPU. For a batch of 1024 evaluations for the conceived optimization algorithm, this is slower than required for the—quite demanding- 5 ms specification of the targeted application. Nevertheless, this also means that providing an efficient hardware interfacing solution, a suitable design is possible also for the FPGA if some adjustment of the use-case specification is made: reducing the batch size to 512 or alternatively either relaxing the cycle time to 10ms or slightly reducing the complexity and precision of the NN.

Another aspect is the scaling proportionality of the computation time, considering that the theoretical growth of computational complexity is 21% for extending the inputs from 16 to 24, as expressed in Table 2. For the FPGA implementation, the penalty grows to 29%. For the GPU, the effect clearly depends on the implementation: while the less efficient GM, GM2 and SM1 solutions suffer a penalty of just 11–14%, SM2 suffers an almost exactly proportional 22%. In contrast, the penalty for extending the inputs on the fine-tuned highly efficient CM version rises to 43%.

8. Conclusions

This work has successfully presented several NN implementations on parallel embedded platforms of different nature, FPGAs and GPUs, integrated in cost-sensitive and industry-suitable SoC devices. Consequently, it provides multiple enabler solutions for the innovative and challenging vehicle dynamics use-case proposed in this paper, as well as for further research also in other fields involving advanced control applications.

For the case of the targeted application, which required fast batch predictions of slip values for a real-time Torque-Vectoring optimization algorithm to control multi-motor electric vehicles, we assessed the technical feasibility of the developed implementations. These were conceived under consideration of the current technological context as well as the automotive domain constraints, which have been reviewed and discussed. Even when fulfilling the highly demanding design specifications defined in this particular use-case, the outcome met or even exceeded the expectations in what respects to both computational performance and accuracy.

The presented work has involved several notable particularities. One is restricting the embedded platforms to industry-suitable devices which due to a lower cost point, energy consumption and size, inevitably represent capacity and performance limitations with respect to typical non-embedded and high-end devices. Another is that the vehicle dynamics predictions corresponding to this application do not require complex NNs of massive dimensions as the ones used in other Machine Learning applications and in the Deep Learning domain. The additional challenge is instead brought by the fact of having to calculate in under 5 ms, the effect of 1024 control actions (with 3 variables each) on 4 highly dynamic variables with a prediction horizon of up to 50 ms.

The GPU implementation has provided an outstanding performance, being two orders of magnitude faster than the FPGA thanks to its great parallelism. But this can only be achieved through very careful programming to maximize occupancy and avoid memory bottlenecks because, in spite of its high memory bandwidth, the high computational throughput can lead to data exchange inefficiencies causing a performance penalty of up to an order of magnitude.

The achieved FPGA implementation of the NN has showed one of the weaknesses of these kind of devices: if the algorithm is too big to be well pipelined, the performance dramatically drops. Consequently, in order to ensure sufficient performance, some compromise solutions need to be adopted in order to satisfy the demanding targeted specifications.

Our analysis also highlights that in cases involving smaller NNs or eventually bigger devices, aiming to achieve full pipelining, FPGAs do have the theoretical potential to provide similar -or even higher- throughput than the selected GPU. This would be beneficial especially for bigger batches of evaluations, to overcome the initial penalty of latency. In contrast, for the non-pipelined implementation shown in this work, the relative efficiency impact of the batch size is marginal for the FPGA, making it more suitable for small batches or for controllers which require a single evaluation per control cycle.

In conclusion this work highlights very clearly fundamental strengths and weaknesses of each platform type, depending on the application specification. Besides the pure performance aspects that have been discussed, while the FPGA is very space-constricted, the instruction-based paradigm of the GPU enables to implement greater functional diversity and to easily scale to bigger algorithms. On the other hand, while the GPU depends on the CPU to operate, the FPGA can run autonomously and could be directly interfaced with sensors and protocols, thus avoiding the initial penalty both platforms are subject to for interfacing with the processor. This would provide another clear benefit for use-cases with few evaluations per cycle on the FPGA.

Ultimately, both embedded platform types have shown their suitability and remarkable potential with the provided implementations. Furthermore, the obtained outcome is a very illustrative example of the fact that, when it comes to discussing the performance of complex highly parallel platforms based on such different execution paradigms, the dependency regarding to the application itself—as well as to the implementation approach- is very significant and needs to be analysed on a per-use-case basis.

9. Future Work

Having confirmed the relevance and feasibility of the application and enablers presented in this paper, future work will take this baseline and go into further depth regarding the application itself, as well as both embedded implementations.

Firstly, using the achieved implementations for very fast embedded NN execution, the benefits of the Torque-Vectoring optimization algorithm itself will be further pursued, paying special attention to the vehicle dynamics performance. Furthermore, the estimation capacities and implications of different NN designs will also be addressed. Besides, a more detailed analysis on the effect of precision loss due to data types and LUT utilization will be considered.

For both embedded implementations, an exhaustive analysis of the interfacing between the heterogeneous parts of the SoC must also be addressed, aiming to minimize the overhead caused by the data exchange. This will not only require careful programming of the interfacing mechanisms but it could also require to conceive solutions where some additional functionalities are integrated in the accelerator part, in order to further reduce the data exchange. For instance, the generation of the batch of values to be evaluated could be integrated. Furthermore, the selection of the best solutions for the optimization could also be accelerated.

Focusing on one platform, the FPGA implementation will be enhanced in different manners. Besides optimizations regarding aspects such as pipelining and data types, a major architectural redesign will be approached. This is conceived to not simply implementing several network layers into the hardware but instead implementing a single cyclically reusable layer, with the capacity of a fast switching between weights and biases corresponding to different layers.

The FPGA will also be used for algorithms involving small batches and single evaluations as discussed in the conclusions, such as virtual sensor functions for current values (Figure 4, bottom left) or for prediction of values not subject to the real-time optimization of different control actions.

On the other hand, the performance of more powerful embedded GPUs for bigger batches and bigger NNs for different applications will also be addressed.

A final topic to be addressed with further depth is functional safety, analysing firstly the criticality of the application as a whole and secondly the criticality of the functionality of the NN. The distribution of functions and protection mechanisms between the processor and the accelerator will require exhaustive analysis, as well as carefully crafted validation approaches. Here, the benefits that the hardware-nature of the FPGA provides in this sense are to be discussed as well.