Improved Ant Colony Algorithm Based on Task Scale in Network on Chip (NoC) Mapping
Abstract
:1. Introduction
2. Performance Model
2.1. Communication Power Model
2.2. Network Latency Model
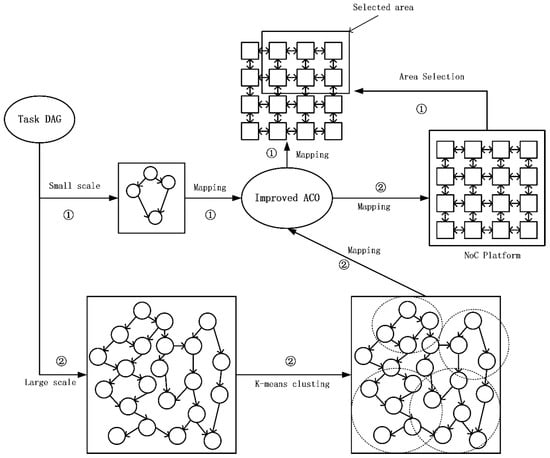
3. Mapping Establishment
3.1. Small-Scale Task Division Scheme
3.2. Large-scale Task Division Scheme
| Algorithm 1 Choice of initial centroid |
| Input: DAG with m tasks; n*n Mesh; Output: k initial centroids center[];/*Centroid to be determined*/ p=0; for task in DAG with outdegree=0 or indegree=0 do task->center[]; p++; end for if p=k then return center[]; end if if p>k then choose the k largest degree with the lager communication tasks; delete other p-k tasks from center[]; else choose the k-p smallest degree with the lager communication tasks; add these k-p tasks into center[]; end if return center[]; |
| Algorithm 2 Iteration process |
| Input: DAG with m tasks n*n Mesh; Initial centroid; Output: Clustering results; c[1],c[2],…,c[k]/*Store clustering results*/ p=0; while Not converged do for task in DAG do Calculate the distance from the task to each centroid; Choose maximum dependent distance; Cluster with this centroid; if No dependencies with centroids then Not clustering temporarily; end if end for Select the task with the largest communication value in each group as the new centroid; end while Divide unclustered tasks into classes with maximum distance dependence; return c[1], c[2],…,c[k]; |
4. Mapping Process
4.1. Algorithm Selection
4.2. Traditional ACO
4.3. Improved ACO
| Algorithm 3 Improved ACO |
| Input: DAG with m tasks; NoC with n*n Mesh; M groups of ants, each with m; Output: bestMapping; procedure Overall process Set maxTimes; while unreach maxTimes do Initialization; Mapping process; Update information; end while return bestMapping; end procedure procedure Initialization AntTable[]; /*Unmapped ants*/ CoreTable[]; /*Unmapped resource nodes*/ Select tasks t without In-degree; Calculate probability p; Map t to resource nodes c based on p; delete t from AntTable[]; delete c from CoreTable[]; end procedure procedure Mapping process while AntTable is not empty do selete task t without parent node or parent is not in AntTable[]; Map t to resource nodes c based on p; delete t from AntTable[]; delete c from CoreTable[]; end while end procedure procedure Update information Calculate communication power and network Latency; if better performance than before then update bestMapping; end if end procedure |
5. Performance Analysis
5.1. Experimental Environment
5.2. Experimental Results
5.2.1. Small Scale Task Mapping Experimental Results
5.2.2. Large Scale Task Mapping Experimental Results
5.3. Experiment Summary
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Renteria-Cedano, J.; Rivera, J.; Sandoval-Ibarra, F.; Ortega-Cisneros, S.; Loo-Yau, R. SoC Design Based on a FPGA for a Configurable Neural Network Trained by Means of an EKF. Electronics 2019, 8, 761. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Zong, H.; Zhao, H.; Cai, H. Intelligent Mapping Method for Power Consumption and Delay Optimization Based on Heterogeneous NoC Platform. Electronics 2019, 8, 912. [Google Scholar] [CrossRef] [Green Version]
- Sahu, P.K.; Shah, T.; Manna, K.; Chattopadhyay, S. Application Mapping Onto Mesh-Based Network-on-Chip Using Discrete Particle Swarm Optimization. IEEE Trans. Larg. Scale Integr. VLSI Syst. 2014, 22, 300–312. [Google Scholar] [CrossRef]
- Khalili, F.; Zarandi, H.R. A Fault-Tolerant Low-Energy Multi-Application Mapping onto NoC-Based Multiprocessors. In Proceedings of the 2012 IEEE 15th International Conference on Computational Science and Engineering, IEEE Computer Society, Nicosia, Cyprus, 5–7 December 2012. [Google Scholar]
- Bayar, S.; Yurdakul, A. An efficient mapping algorithm on 2-D mesh Network-on-Chip with reconfigurable switches. In Proceedings of the International Conference on Design Technology of Integrated Systems in Nanoscale Era, Istanbul, Turkey, 12–14 April 2016. [Google Scholar]
- Seidipiri, R.; Patooghy, A.; Afsharpour, S.; Fazeli, M. RASMAP: An efficient heuristic application mapping algorithm for network-on-chips. In Proceedings of the Eighth International Conference on Information Knowledge Technology, Hamedan, Iran, 7–8 September 2016. [Google Scholar]
- Sacanamboy, M.; Quesada, L.; Bolanos, F.; Bernal, A.; O’Sullivan, B. A Comparison between Two Optimisation Alternatives for Mapping in Wireless Network on Chip. In Proceedings of the IEEE International Conference on Tools with Artificial Intelligence, San Jose, CA, USA, 6–8 November 2016. [Google Scholar]
- Shekhar, M.; Ramaprasad, H.; Mueller, F. Network-on-Chip aware scheduling of hard-real-time tasks. In Proceedings of the 9th IEEE International Symposium on Industrial Embedded Systems (SIES 2014), Pisa, Italy, 18–20 June 2014; pp. 141–150. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Zhang, D.; Huang, C. Research on low-power mapping for three-dimensional network-on-chip based on inproved genetic algorithm. Comput. Eng. Appl. 2016. [Google Scholar] [CrossRef]
- Yi, L.; Niu, Y.T.; Xu, C.Q. Configurable links for 3D network on-chip based on mapping algorithm. In Proceedings of the IEEE International Conference on Solid-state Integrated Circuit Technology, Hangzhou, China, 25–28 October 2016. [Google Scholar]
- Liu, L.; Wu, C.; Deng, C.; Yin, S.; Wu, Q.; Han, J.; Wei, S. A Flexible Energy-and Reliability-Aware Application Mapping for NoC-Based Reconfigurable Architectures. IEEE Trans. Larg. Scale Integr. Syst. 2015, 23, 2566–2580. [Google Scholar] [CrossRef]














© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Yu, T.; Wei, Z. Improved Ant Colony Algorithm Based on Task Scale in Network on Chip (NoC) Mapping. Electronics 2020, 9, 6. https://doi.org/10.3390/electronics9010006
Fang J, Yu T, Wei Z. Improved Ant Colony Algorithm Based on Task Scale in Network on Chip (NoC) Mapping. Electronics. 2020; 9(1):6. https://doi.org/10.3390/electronics9010006
Chicago/Turabian StyleFang, Juan, Tingwen Yu, and Zelin Wei. 2020. "Improved Ant Colony Algorithm Based on Task Scale in Network on Chip (NoC) Mapping" Electronics 9, no. 1: 6. https://doi.org/10.3390/electronics9010006
APA StyleFang, J., Yu, T., & Wei, Z. (2020). Improved Ant Colony Algorithm Based on Task Scale in Network on Chip (NoC) Mapping. Electronics, 9(1), 6. https://doi.org/10.3390/electronics9010006