Flux Coupling and the Objective Functions’ Length in EFMs
Abstract
:1. Introduction
- The relationship between the number of repeated solutions and the length of the objective functions used.
- The use of negative constraints as a means of improving the diversity of the solutions obtained.
- The development of a new proposal (FLFS-FC) to obtain large sets of EFMs. This proposal has efficiency rates far better than previously proposed ones.
2. Results
3. Discussion
4. Material and Methods
4.1. Definitions and Background
4.2. Finding EFMs by Solving LP Problems
- A vector with to define the linear function f to be minimized.
- A subset to add a unique positive constraint to avoid trivial solutions.
- Optionally, a subset to add an optional negative constraint.
- Strategy 1.—Fix the linear function f and vary the positive constraint. In this case:
- –
- We will use the linear function .
- –
- At every step, we randomly choose a set of reactions and add the positive constraint associated with them.
- Strategy 2.—Fix the positive constraint and vary the function f
- –
- We will use the linear constraint .
- –
- At every step we randomly choose non-negative values () and try to minimize the associated function .
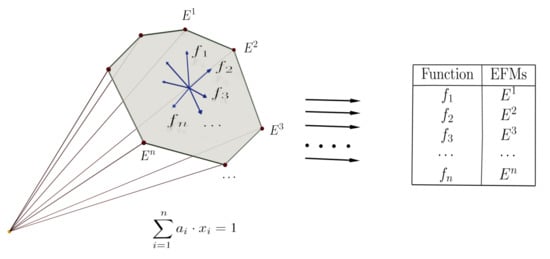
4.3. Enhancing the Election of Objective Functions
- If , then the set of possible extreme solutions of this problem is is an EFM, and
- Given an EFM, E, of the network, it is always possible to find a subset J and a reaction r such that E is an extreme solution of the posed LP problem with
- Observe that, for any solution , is equivalent to saying that and, due to the additional constraint imposed, we must have . Finally, by using Theorem 2, we obtain that all possible extreme solutions of the problem are EFMs.
- For any reaction , define , and the additional constraint . We haveClearly and this is the optimal value for f (for any other solution of the problem v, we must have and so ). Furthermore, E is the unique minimal solution, because any other solution v must accomplish that and E is an EFM. Therefore, E is an extreme solution of the LP problem.
- 1.
- Starting with the target reaction r we calculate , where n is the number of reactions and p the proportion of reactions used to compute the objective functions. A list to store the supports of the EFMs computed is defined.
- 2.
- In each step, we randomly generate a list J of reactions of length equal to k. This list defines a linear function f whose coefficients correspond to indices that are in J and are set equal to random numbers between 0 and 1. The remaining coefficients are set to 0.
- 3.
- We pose the LP problem of minimizing f with the stoichiometric and thermodynamic constraints and also add the constraint .
- 4.
- Let E be the solution returned by the solver. We then compute its support and, if it has not been previously computed, it is added to the list of the obtained supports.
| Algorithm 1: Algorithm to extract EFMs from a metabolic network |
 |
4.4. Improving the Efficiency Rates Using Negative Constraints
| Algorithm 2: FLFS-FC algorithm to extract EFMs from a metabolic network |
 |
Author Contributions
Funding
Conflicts of Interest
Availability of Data Materials
References
- Bazzani, S. Promise and reality in the expanding field of network interaction analysis: Metabolic networks. Bioinform Biol. Insights 2014, 8, 83–91. [Google Scholar] [CrossRef] [PubMed]
- Covert, M.W.; Palsson, B.Ø. Constraints-based models: Regulation of gene expression reduces the steady-state solution space. J. Theor. Biol. 2003, 221, 309–325. [Google Scholar] [CrossRef] [Green Version]
- Palsson, B.Ø. The challenges of in silico biology. Nat. Biotechnol. 2000, 18, 1147–1150. [Google Scholar] [CrossRef]
- Schilling, C.H.; Letscher, D.; Palsson, B.Ø. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J. Theor. Biol. 2000, 203, 229–248. [Google Scholar] [CrossRef] [Green Version]
- Gagneur, J.; Klamt, S. Two approaches for metabolic pathway analysis? BMC Bioinform. 2004, 5, 175. [Google Scholar] [CrossRef] [Green Version]
- Schuster, S.; Hilgetag, C. On elementary flux modes in biochemical reaction systems at steady state. J. Biol. Syst. 1994, 2, 165–182. [Google Scholar] [CrossRef]
- Klamt, S.; Stelling, J. Computation of elementary modes: A unifying framework and the new binary approach. Trends Biotechnol. 2003, 21, 64–69. [Google Scholar] [CrossRef]
- Pfeiffer, T.; Sanchez-Valdenebro, I.; Nuno, J.C.; Montero, F.; Schuster, S. METATOOL: For studying metabolic networks. Bioinformatics 1999, 15, 251–257. [Google Scholar] [CrossRef] [Green Version]
- Tefagh, M.; Boyd, S.P. Quantitative flux coupling analysis. J. Math. Biol. 2019, 78, 1459–1484. [Google Scholar] [CrossRef]
- Klamt, S.; Gilles, E.D. Minimal cut sets in biochemical reaction networks. Bioinformatics 2004, 20, 226–234. [Google Scholar] [CrossRef]
- Klamt, S.; Stelling, J. Combinatorial complexity of pathway analysis in metabolic networks. J. Mol. Biol. Rep. 2002, 29, 233–236. [Google Scholar] [CrossRef] [PubMed]
- Yeung, M.; Thiele, I.; Palsson, B.Ø. Estimation of the number of extreme pathways for metabolic networks. BMC Bioinform. 2007, 8, 363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bohl, K.; Figueiredo, L.F.D.; Hädicke, O.; Klamt, S.; Kost, C.; Schuster, S.; Kaleta, C. CASOP GS: Computing intervention strategies targeted at production improvement in genome-scale metabolic networks. In Proceedings of the 25th German Conference on Bioinformatics, Braunschweig, Germany, 20–22 September 2010; pp. 71–80. [Google Scholar]
- Kaleta, C.; Figueiredo, L.F.D.; Behre, J.; Schuster, S. Efmevolver: Computing elementary flux modes in genome-scale metabolic networks. Lect. Notes Inform. Proc. 2009, 157, 179–189. [Google Scholar]
- Machado, D.; Soons, Z.; Patil, K.R.; Ferreira, E.C.; Rocha, I. Random sampling of elementary flux modes in large-scale metabolic networks. Bioinformatics 2012, 28, I515–I521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fukuda, K.; Prodon, A. Double descriptionmethod revisited. Comb. Comput. Sci. 1996, 1120, 91–111. [Google Scholar]
- Terzer, M.; Stelling, J. Large-scale computation of elementary flux modes with bit pattern trees. Bioinformatics 2008, 24, 2229–2235. [Google Scholar] [CrossRef] [PubMed]
- De Figueiredo, L.F.; Podhorski, A.; Rubio, A.; Kaleta, C.; Beasley, J.E.; Schuster, S.; Planes, F.J. Computing the shortest elementary flux modes in genome-scale metabolic networks. Bioinformatics 2009, 25, 3158–3165. [Google Scholar] [CrossRef]
- Rezola, A.; de Figueiredo, L.F.; Brock, M.; Pey, J.; Podhorski, A.; Wittmann, C.; Schuster, S.; Bockmayr, A.; Planes, F.J. Exploring metabolic pathways in genome-scale networks via generating flux modes. Bioinformatics 2011, 27, 534–540. [Google Scholar] [CrossRef] [Green Version]
- Pey, J.; Villar, J.A.; Tobalina, L.; Rezola, A.; García, J.M.; Beasley, J.E.; Planes, F.J. Treeefm: Calculating elementary flux modes using linear optimization in a tree-based algorithm. Bioinformatics 2015, 31, 897–904. [Google Scholar] [CrossRef] [Green Version]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.Ø. A genome-scale metabolic reconstruction for escherichia coli k-12 mg1655 that accounts for 1260 orfs and thermodynamic information. Mol. Syst. Biol. 2007, 3, 121. [Google Scholar] [CrossRef]
- Klamt, S.; Gagneur, J.; Von Kamp, A. Algorithmic approaches for computing elementary modes in large biochemical reaction networks. IEE Proc. Syst. Biol. 2005, 152, 249–255. [Google Scholar] [CrossRef] [PubMed]
- Acuna, V.; Chierichetti, F.; Lacroix, V.; Marchetti-Spaccamela, A.; Sagot, M.F.; Stougie, L. Modes and cuts in metabolic networks: Complexity and algorithms. Biosystems 2009, 95, 51–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hidalgo, J.F.; Guil, F.; García, J.M. Computing EFM’s using balanced subgraphs and boolean logic. In Proceedings of the 4th International Work-Conference on Bioinformatics and Biomedical Engineering (IWBBIO 2016), Granada, Spain, 20–22 April 2016; pp. 1–8. [Google Scholar]
- Morterol, M.; Dague, P.; Peres, S.; Simon, L. Minimality of metabolic flux modes under boolean regulation constraints. In Proceedings of the 12th International Workshop on Constraint-Based Methods for Bioinformatics (WCBl16), Toulouse, France, 5 September 2016; pp. 65–81. [Google Scholar]
- Pey, J.; Planes, F.J. Direct calculation of elementary flux modes satisfying several biological constraints in genome-scale metabolic networks. Bioinformatics 2014, 30, 2197–2203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hidalgo, J.F.; Egea, J.A.; Guil, F.; García, J.M. Representativeness of a set of metabolic pathways. In Bioinformatics and Biomedical Engineering; Springer International Publishing: Granada, Spain, 2017; Volume 10208, pp. 659–667. [Google Scholar]
- Schellenberger, J.; Park, J.O.; Conrad, T.M.; Palsson, B.Ø. Bigg: A biochemical genetic and genomic knowledgebase of large scale metabolic reconstructions. BMC Bioinform. 2010, 11, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Acuña, V.; Marchetti-Spaccamela, A.; Sagot, M.F.; Stougie, L. A note on the complexity of finding and enumerating elementary modes. Biosystems 2009, 99, 210–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burgard, A.P.; Nikolaev, E.V.; Schilling, C.H.; Maranas, C. Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res. 2004, 14, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Larhlimi, A.; David, L.; Selbig, J.; Bockmayr, A. F2C2: A fast tool for the computation of flux coupling in genome-scale metabolic networks. BMC Bioinform. 2012, 13, 57. [Google Scholar] [CrossRef] [Green Version]


| Compound | EFMevolver | treeEFM | FLFS-FC | |I| | |K| | Relative Improvement |
|---|---|---|---|---|---|---|
| L-Lysine | 2.23 | 1.38 | 1.017 | 70 | 32 | 22.35 |
| L-Threonine | 1.90 | 1.64 | 1.009 | 70 | 4 | 66.66 |
| L-Arginine | 1.80 | 1.67 | 1.014 | 70 | 3 | 47.85 |
| Number of EFMs | Efficiency Rate | Computation Time |
|---|---|---|
| 20,000 | 1.0611 | 782.6315 |
| 200,000 | 1.1806 | 8044.6168 |
| 400,000 | 1.2277 | 16,972.4034 |
| 600,000 | 1.2583 | 26,785.2445 |
| 800,000 | 1.2964 | 37,428.8663 |
| 1,000,000 | 1.3246 | 48,881.2113 |
| Strategy | Efficiency Rate |
|---|---|
| Randomizing additional constraint | 8.08 |
| Randomizing objective function | 1.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guil, F.; Hidalgo, J.F.; García, J.M. Flux Coupling and the Objective Functions’ Length in EFMs. Metabolites 2020, 10, 489. https://doi.org/10.3390/metabo10120489
Guil F, Hidalgo JF, García JM. Flux Coupling and the Objective Functions’ Length in EFMs. Metabolites. 2020; 10(12):489. https://doi.org/10.3390/metabo10120489
Chicago/Turabian StyleGuil, Francisco, José F. Hidalgo, and José M. García. 2020. "Flux Coupling and the Objective Functions’ Length in EFMs" Metabolites 10, no. 12: 489. https://doi.org/10.3390/metabo10120489
APA StyleGuil, F., Hidalgo, J. F., & García, J. M. (2020). Flux Coupling and the Objective Functions’ Length in EFMs. Metabolites, 10(12), 489. https://doi.org/10.3390/metabo10120489