Satellite Excitations and Final State Interactions in Atomic Photoionization
Abstract
:1. Introduction
2. Theoretical Approach
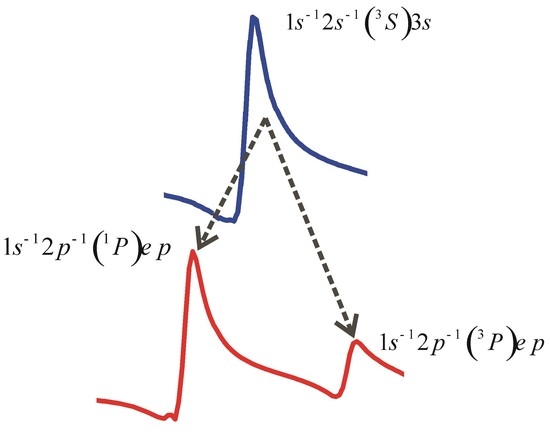
3. Noble Gases
4. Atoms in Chemical Compounds
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wendin, G. Breakdown of one-electron pictures in photoelectron spectra. In Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 1981; Volume 45, pp. 1–125. ISBN 978-3662157800. [Google Scholar]
- Kowalczyk, S.P.; Ley, L.; Martin, R.L.; McFeely, F.R.; Shirley, D.A. Relaxation and final-state structure in XPS of atoms, molecules, and metals. Faraday Discuss. Chem. Soc. 1975, 60, 7–17. [Google Scholar] [CrossRef] [Green Version]
- Sham, T.K.; Wendin, G. Screening and configuration-interaction effects in the 5p X-ray-photoelectron spectrum of Th metal. Phys. Rev. Lett. 1980, 44, 817–820. [Google Scholar] [CrossRef]
- Boring, M.; Cowan, R.D. Satellite structure in the 5p and 5s X-ray-photoelectron spectra of the actinides. Phys. Rev. B 1981, 23, 445–448. [Google Scholar] [CrossRef]
- Fadley, C.S.; Shirley, D.A. Multiplet splitting of metal-atom electron binding energies. Phys. Rev. A 1970, 2, 1109–1113. [Google Scholar] [CrossRef] [Green Version]
- Kowalczyk, S.P.; Ley, L.; Pollak, R.A.; McFeely, F.R.; Shirley, D.A. New multiplet structure in photemission from MnF2. Phys. Rev. B 1973, 7, 4009–4011. [Google Scholar] [CrossRef] [Green Version]
- Viinikka, E.-K.; Ohrn, Y. Configuration mixing in the 3s-hole state of transition-metal ion. Phys. Rev. B 1975, 11, 4168–4175. [Google Scholar] [CrossRef]
- Bagus, P.S.; Freeman, A.J.F.; Sasaki, F. Prediction of new multiplet structure in photoemission experiments. Phys. Rev. 1975, 30, 850–853. [Google Scholar] [CrossRef]
- Bagus, P.S.; Broer, R.; Ilton, E.S. A new near degeneracy effect for photoemission in transition metals. Chem. Phys. Lett. 2004, 394, 150–154. [Google Scholar] [CrossRef]
- Kochur, A.G.; Ivanova, T.M.; Shchukarev, A.V.; Sidorov, A.A.; Kiskin, M.A.; Novotortsev, V.M.; Eremenko, I.L. Mn3s X-ray photoelectron spectra of polynuclear trimethylacetate complexes of manganese. Bull. Russ. Acad. Sci. Phys. 2010, 74, 625–630. [Google Scholar] [CrossRef]
- Okada, K.; Kotani, A. Interatomic and intra-atomic configuration interactions in core-level X-ray photoemission spectra of late transition metal compounds’. J. Phys. Soc. Jpn. 1992, 61, 4619–4637. [Google Scholar] [CrossRef]
- Svensson, S.; Eriksson, B.; Martensson, N.; Wendin, G.; Gelius, U. Electron shake-up and correlation satellites and continuum shake-off distributions in X-ray photoelectron spectra of the rare gas atoms. J. Electron Spectrosc. Relat. Phenom. 1988, 47, 327–384. [Google Scholar] [CrossRef]
- Pahler, M.; Caldwell, C.D.; Schaphorst, S.J.; Krause, M.O. Intrinsic linewidths of neon 2s2p5 (1,3P)nl 2L correlation satellites. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 1617–1625. [Google Scholar] [CrossRef]
- Hall, R.I.; Dawber, G.K.; Ellis, K.; Zubek, M.; Avaldi, L.; King, G.C. Near-threshold study of the neon photoelectron satellites. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 4133–4146. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Amusia, M.Y.; Bolognesi, P.; Avaldi, L. A study of the Ne 2s2p5(3P)3s and 3p correlation satellites up to 75 eV above threshold. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 185204. [Google Scholar] [CrossRef]
- Krause, M.O.; Whitfield, S.B.; Caldwell, C.D.; Wu, J.-Z.; Schaphorst, S.J.; van der Meulen, P.; de Lange, C.A.; Hansen, R.W.C. Outer ns, np correlation satellites in the rare gases—A photoelectron spectrometry study with an undulator photon source. J. Electron Spectrosc. Relat. Phenom. 1992, 58, 79–104. [Google Scholar] [CrossRef]
- Kikas, A.; Osborne, S.J.; Ausmees, A.; Svensson, S.; Sairanen, O.-P.; Aksela, S. High-resolution study of the correlation satellites in photoelectron spectra of the rare gases. J. Electron Spectrosc. Relat. Phenom. 1996, 77, 241–266. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Nefedov, V.I.; Trzhaskovskaya, M.B.; Band, I.M.; Szargan, R. The influence of core hole relaxation on the main-line intensities in X-ray photoelectron spectra. J. Electron Spectrosc. Relat. Phenom. 2002, 123, 1–10. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Trzhaskovskaya, M.B. Spectroscopic factors of atomic subshells for HAXPES applications. At. Data Nucl. Data Tables 2021, 139, 101387. [Google Scholar] [CrossRef]
- Seah, M.P.; Gilmore, I.S. Quantitative X-ray photoelectron spectroscopy: Quadrupole effects, shake-up, Shirley background, and relative sensitivity factors from a database of true X-ray photoelectron spectra. Phys. Rev. B 2006, 73, 174113, Erratum in Phys. Rev. B 2007, 75, 149901. [Google Scholar] [CrossRef]
- Åberg, T. Theory of X-ray satellites. Phys. Rev. 1967, 156, 35–41. [Google Scholar] [CrossRef]
- Manne, R.; Åberg, T. Koopmans’ theorem for inner-shell ionization. Chem. Phys. Lett. 1970, 2, 282–284. [Google Scholar] [CrossRef]
- Martin, R.L.; Shirley, D.A. Theory of core-level photoemission correlation state spectra. J. Chem. Phys. 1976, 64, 3685–3689. [Google Scholar] [CrossRef] [Green Version]
- Armen, G.B.; Åberg, T.; Karim, K.R.; Levin, J.C.; Crasemann, B.; Brown, G.S.; Chen, M.H.; Ice, G.E. Threshold double photoexcitation of argon with synchrotron radiation. Phys. Rev. Lett. 1985, 54, 182–185. [Google Scholar] [CrossRef] [PubMed]
- Sukhorukov, V.L.; Lagutin, B.M.; Petrov, I.D.; Schmoranzer, H.; Ehresmann, A.; Vollweiler, F.; Schartner, K.-H. Resonance structure of the photoionization cross sections of the Kr atom in the energy region between single and double ionization thresholds. J. Electron Spectrosc. Relat. Phenom. 1995, 76, 421–426. [Google Scholar] [CrossRef]
- Lagutin, B.M.; Petrov, I.D.; Sukhorukov, V.L.; Whitfield, S.B.; Langer, B.; Viefhaus, J.; Wehlitz, R.; Berrah, N.; Mahler, W.; Becker, U. Cross sections and angular distributions of the photoelectron correlation satellites of the Xe atom. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 937–976. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Amusia MYa Yarzhemsky, V.G. On the validity of quasi-particle approximation in photoelectron spectroscopy. J. Phys. B. At. Mol. Opt. Phys. 1985, 18, L343–L350. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Armen, G.B.; Larkins, F.P. Calculation of the shake-up satellites in the 1s and 2s X-ray photoelectron spectra of neon. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 2785–2794. [Google Scholar] [CrossRef]
- Kheifets, A.S. Green’s function calculation of the satellite spectrum of neon. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 3791–3803. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Kheifets, A.S.; Armen, G.B.; Larkins, F.P. Linewidths and intensities of satellites in photoelectron spectra in the presence of an underlying continuum. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 2105–2112. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Larkins, F.P. The shapes of Auger decay lines in photoelectron satellite spectra. Eur. Phys. J. D At. Mol. Opt. Plasma Phys. 1999, 5, 179–184. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Amusia, M.Y.; Chernysheva, L.V. Lineshape of Ne 1s photoionization satellite [1s2s](3S) 3s and its valence Auger decay spectrum. J. Electron Spectrosc. Relat. Phenom. 2002, 127, 153–159. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Nefedov, V.I.; Amusia MYa Chernysheva, L.V. The shapes of photoelectron satellite spectra. Surf. Rev. Lett. 2002, 9, 1209–1212. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Sgamellotti, A. Auger rates of second-row atoms calculated by many-body perturbation theory. J. Electron Spectrosc. Relat. Phenom. 2002, 125, 13–24. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Yarzhemsky, V.G. Handbook of Theoretical Atomic Physics; Springer: Berlin/Heidelberg, Germany, 2012; p. 799. [Google Scholar] [CrossRef] [Green Version]
- Kaneyasu, T.; Hikosaka, Y.; Shigemasa, E.; Penent, F.; Lablanquie, P.; Aoto, T.; Ito, K. Autoionization of the Ne+ Rydberg states formed via valence photoemission. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 4047–4060. [Google Scholar] [CrossRef]
- Hikosaka, Y.; Aoto, T.; Lablanquie, P.; Penent, F.; Shigemasa, E.; Ito, K. Experimental investigation of core-valence double photoionization. Phys. Rev. Lett. 2006, 97, 053003. [Google Scholar] [CrossRef]
- Püttner, R.; Goldsztejn, G.; Céolin, D.; Rueff, J.-P.; Moreno, T.; Kushawaha, R.K.; Marchenko, T.; Journel, L.; Lindle, D.W.; Piancastelli, M.N.; et al. Direct Observation of Double-Core-Hole Shake-Up States in Photoemission. Phys. Rev. Lett. 2015, 114, 093001. [Google Scholar] [CrossRef]
- Goldsztejn, G.; Marchenko, T.; Püttner, R.; Journel, L.; Guillemin, R.; Carniato, S.; Selles, P.; Travnikova, T.; Céolin, D.; Lago, A.F.; et al. Double-Core-Hole States in Neon: Lifetime, Post-Collision Interaction, and Spectral Assignment. Phys. Rev. Lett. 2016, 117, 133001. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Yarzhemsky, V.G. On photoionization in the hard X-ray region. JETP Lett. 2013, 97, 704–707. [Google Scholar] [CrossRef] [Green Version]
- Yarzhemsky, V.G.; Amusia, M.Y. Calculation of Ar photoelectron satellites in the hard-X-ray region. Phys. Rev. A 2016, 93, 063406. [Google Scholar] [CrossRef] [Green Version]
- Yarzhemsky, V.G.; Teterin, Y.A.; Presnyakov, I.A.; Maslakov, K.I.; Teterin, A.Y.; Ivanov, K.E. Many-electron effects in Co 3s X-ray photoelectron spectra of diamagnetic ScCoO3 and paramagnetic BiCoO3 Cobaltites. JETP Lett. 2020, 111, 422–427. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Teterin, Y.A.; Sosulnikov, M.I. Dynamic dipolar relaxation in X-ray photoelectron spectra of Ba4p subshell in barium compounds. J. Electron Spectrosc. Relat. Phenomom. 1992, 59, 211–222. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Teterin Yu, A.; Maslakov, K.I.; Teterin, A.Y.; Ivanov, K.E. Many-electron effects in Th 5p and 5s X-ray photoelectron spectra of ThO2. JETP Lett. 2021, 114, 609–615. [Google Scholar] [CrossRef]
- Maslakov, K.I.; Yarzhemsky, V.G.; Teterin, Y.A.; Teterin, A.Y.; Ivanov, K.E. Complex XPS spectra structure of U5p electrons and the uranium oxidation state. Radiochemistry 2020, 62, 608–616. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V. Computation of Atomic Processes; IOP Publishing: Bristol/Philadelphia, PA, USA, 1997; ISBN 9780750302296. [Google Scholar]
- Amusia, M.Y.; Chernysheva, L.V. Computation of atomic and molecular processes. In Introducing the ATOM-M Software Suite; Springer: Berlin/Heidelberg, Germany, 2021; p. 456. ISBN 978-3-030-85142-2. [Google Scholar]
- Lindgren, I.; Morrison, J. Atomic Many-Body Theory; Springer: Berlin/Heidelberg, Germany, 1982; p. 472. ISBN 978-3-642-96614-9. [Google Scholar]
- Judd, B.R. Second Quantization and Atomic Spectroscopy; Baltimore MD Johns Hopkins press: Baltimore, MD, USA, 1967; ISBN 0801803225/9780801803222. [Google Scholar]
- Walters, D.L.; Bhalla, C.P. Nonrelativistic auger Rates, X-ray rates, and fluorescence yields for the K shell. Phys. Rev. A 1971, 3, 1919–1926. [Google Scholar] [CrossRef]
- Sobelman, I.I. Atomic spectra and radiative transitions. In Chemical Physics Book Series (CHEMICAL, V. 1); Springer: Berlin/Heidelberg, Germany, 1979; p. 308. ISBN 978-3-662-05905-0. [Google Scholar]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yarzhemsky, V.G.; Teterin, Y.A. Satellite Excitations and Final State Interactions in Atomic Photoionization. Atoms 2022, 10, 73. https://doi.org/10.3390/atoms10030073
Yarzhemsky VG, Teterin YA. Satellite Excitations and Final State Interactions in Atomic Photoionization. Atoms. 2022; 10(3):73. https://doi.org/10.3390/atoms10030073
Chicago/Turabian StyleYarzhemsky, Victor G., and Yury A. Teterin. 2022. "Satellite Excitations and Final State Interactions in Atomic Photoionization" Atoms 10, no. 3: 73. https://doi.org/10.3390/atoms10030073
APA StyleYarzhemsky, V. G., & Teterin, Y. A. (2022). Satellite Excitations and Final State Interactions in Atomic Photoionization. Atoms, 10(3), 73. https://doi.org/10.3390/atoms10030073