Exploring Protein Fold Space
Abstract
:1. Protein Fold Space
1.1. Early Explorers
1.2. Visualising Protein Fold-Space
2. Protein Topology
2.1. Topological Metrics
2.2. Topology Diagrams
2.3. Topology String Representation
2.4. Comparing Topology Strings
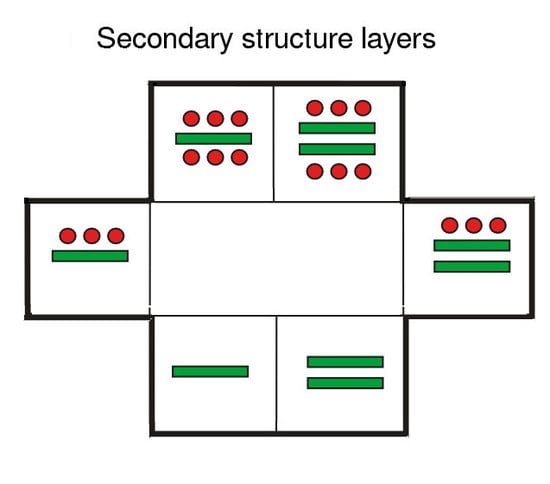
3. Secondary Structure Lattices
3.1. Ideal Forms
- 1-4+6-1 0-4+6-1 0-4+6-0
- 1-4+6-2 0-4+6-2 :
- 1-4+6-3 0-4+6-3 :
- 2-4+6-3 : :
- 2-4+6-3 : :
- 2-4+6-3 : :
- 1-5+6-1 0-5+6-1 0-5+6-0
3.2. Generating A Fold-Space
4. Generalised Lattices
4.1. Missing Types
4.2. Deltahedra and Tetrahedron “Packing”
4.3. Penrose Tiling and Quasi-Lattices
4.4. Chain Tracing over A Lattice
4.5. Testing Different Lattices
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ptitsyn, O.B.; Rashin, A.A. A model of myoglobin self-organisation. Biophys. Chem. 1975, 3, 1–20. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Ptitsyn, O.B. A theory of protein molecule self-organization. IV. Helical and irregular local structures of unfolded protein chains. J. Mol. Biol. 1976, 103, 15–24. [Google Scholar] [CrossRef]
- Nagano, K. Logical analysis of the mechanism of protein folding. IV. Super-secondary structures. J. Mol. Biol. 1977, 109, 235–250. [Google Scholar] [CrossRef]
- Sternberg, M.; Thornton, J. On the conformation of proteins: The handedness of the β-strand-α-helix-β-strand unit. J. Mol. Biol. 1976, 105, 367–382. [Google Scholar] [CrossRef]
- Banner, D.W.; Bloomer, A.C.; Petsko, G.A.; Phillips, D.C.; Pogson, C.I.; Wilson, I.A.; Corran, P.H.; Furth, A.J.; Milman, J.D.; Offord, R.E.; et al. Structure of chicken muscle triose phosphate isomerase determined crystallographically at 2.5Å resolution: Using amino acid sequence data. Nature 1975, 255, 609–614. [Google Scholar] [CrossRef] [PubMed]
- Phillips, D.; Sternberg, M.; Thornton, J.; Wilson, I. An analysis of the structure of triose phosphate isomerase and its comparison with lactate dehydrogenase. J. Mol. Biol. 1978, 119, 329–351. [Google Scholar] [CrossRef]
- Richardson, J.S. Handedness of crossover connections in β-sheets. Proc. Natl. Acad. Sci. USA 1976, 74, 2619–2623. [Google Scholar] [CrossRef] [Green Version]
- Richardson, J.S. β-Sheet topology and the relatedness of proteins. Nature 1977, 268, 495–500. [Google Scholar] [CrossRef]
- Efimov, A. Standard structures in proteins. Prog. Biophys. Mol. Biol. 1993, 60, 201–239. [Google Scholar] [CrossRef]
- Efimov, A.V. Structural trees for protein superfamilies. Proteins: Struct. Funct. Bioinform. 1997, 28, 241–260. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Reva, B.A. A search for the most stable folds of protein chains. Nature 1991, 351, 497–499. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R.; Orengo, C.A. Protein structure alignment. J. Mol. Biol. 1989, 208, 1–22. [Google Scholar] [CrossRef]
- Holm, L.; Sander, C. Protein Structure Comparison by Alignment of Distance Matrices. J. Mol. Biol. 1993, 233, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Orengo, C.; Flores, T.; Taylor, W.; Thornton, J. Identification and classification of protein fold families. Protein Eng. Des. Sel. 1993, 6, 485–500. [Google Scholar] [CrossRef]
- Levitt, M.; Chothia, C. Structural patterns in globular proteins. Nature 1976, 261, 552–558. [Google Scholar] [CrossRef]
- Hou, J.; Sims, G.E.; Zhang, C.; Kim, S.-H. A global representation of the protein fold space. Proc. Natl. Acad. Sci. USA 2003, 100, 2386–2390. [Google Scholar] [CrossRef] [Green Version]
- Taylor, W.R.; Orengo, C.A. A holistic approach to protein structure comparison. Prot. Eng. 1989, 2, 505–519. [Google Scholar] [CrossRef]
- Grindley, H.M.; Artymiuk, P.J.; Rice, D.W.; Willett, P. Identificaton of tertiary structure resemblance in proteins using a maximal common sub-graph isomorphism algorithm. J. Molec. Biol. 1993, 229, 707–721. [Google Scholar] [CrossRef]
- Johannissen, L.O.; Taylor, W.R. Protein fold comparison by the alignment of topological strings. Protein Eng. Des. Sel. 2003, 16, 949–955. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Ptitsyn, O.B. Why do globular proteins fit the limited set of folding patterns? Prog. Biophys. Molec. Biol. 1987, 50, 171–190. [Google Scholar] [CrossRef]
- Chothia, C.; Finkelstein, A.V. The classification and origins of protein folding patterns. Ann. Rev. Biochem. 1990, 59, 1007–1039. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R. A ‘periodic table’ for protein structures. Nature 2002, 416, 657–660. [Google Scholar] [CrossRef] [PubMed]
- Hollup, S.M.; Sadowski, M.I.; Jonassen, I.; Taylor, W.R. Exploring the limits of fold discrimination by structural alignment: a large scale benchmark using decoys of known fold. Comput. Biol. Chem. 2011, 35, 174–188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, W.R.; Chelliah, V.; Hollup, S.M.; Macdonald, J.T.; Jonassen, I. Probing the “Dark Matter” of Protein Fold Space. Structuce 2009, 17, 1244–1252. [Google Scholar] [CrossRef] [Green Version]
- Murzin, A.G.; Finkelstein, A.V. General architecture of the α-helical globule. J. Mol. Biol. 1988, 204, 749–769. [Google Scholar] [CrossRef]
- Taylor, W.R.; Jones, D.T.; Green, N.M. A method for α-helical integral membrane protein fold prediction. Proteins Struct. Funct. Bioinform. 1994, 18, 281–294. [Google Scholar] [CrossRef]
- Finney, J.L. Random packings and the structure of simple liquids. Proc. Roy. Soc. 1970, A319, 479–493. [Google Scholar]
- Grainger, B.; Sadowski, M.I.; Taylor, W.R. Re-Evaluating the “Rules” of Protein Topology. J. Comput. Biol. 2010, 17, 1371–1384. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Badretdinov, A.Y.; Gutin, A.M. Why do protein architectures have Boltzmann-like statistics? Prot. Struct. Funct. Genet. 1995, 23, 142–150. [Google Scholar] [CrossRef]
- Finkelstein, A.V.; Bogatyreva, N.S.; Garbuzynskiy, S.O. Restrictions to protein folding determined by the protein size. FEBS Lett. 2013, 587, 1884–1890. [Google Scholar] [CrossRef] [Green Version]











© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taylor, W.R. Exploring Protein Fold Space. Biomolecules 2020, 10, 193. https://doi.org/10.3390/biom10020193
Taylor WR. Exploring Protein Fold Space. Biomolecules. 2020; 10(2):193. https://doi.org/10.3390/biom10020193
Chicago/Turabian StyleTaylor, William R. 2020. "Exploring Protein Fold Space" Biomolecules 10, no. 2: 193. https://doi.org/10.3390/biom10020193
APA StyleTaylor, W. R. (2020). Exploring Protein Fold Space. Biomolecules, 10(2), 193. https://doi.org/10.3390/biom10020193