Is Medoid Suitable for Averaging GPS Trajectories?
Abstract
:1. Introduction
- What is the accuracy of the medoid?
- When does it work and when not?
- Does it work better than existing averaging techniques in the case of noisy data?
- Which similarity function works best, and how much does the choice matter?
2. Segment Averaging
2.1. Heuristics for Finding Segment Mean
2.2. Medoid
2.3. Hybrid of Heuristics and Medoid
3. Similarity Measures
3.1. Cell Similarity (C-SIM)
3.2. Hierarchical Cell Similarity (HC-SIM)
3.3. Euclidean Distance
3.4. Longest Common Subsequence (LCSS)
3.5. Edit Distance on Real Sequence (EDR)
3.6. Dynamic Time Warping (DTW)
3.7. Edit Distance with Real Penalty (ERP)
3.8. Fréchet and Hausdorff Distances
3.9. Interpolated Route Distance (IRD)
4. Experimental Setup
- Segment averaging [7]http://cs.uef.fi/sipu/segments/training.html (accessed on 24 November 2021)
- Road-network extraction [25]http://cs.uef.fi/mopsi/routes/network (accessed on 24 November 2021)
- Similarity of trajectories [5]http://cs.uef.fi/mopsi/routes/similarityApi/demo.php (accessed on 24 November 2021)
- Transport-mode detection [46]http://cs.uef.fi/mopsi/routes/transportationModeApi (accessed on 24 November 2021)
- Trajectory reduction [47]http://cs.uef.fi/mopsi/routes/reductionApi (accessed on 24 November 2021)
- Tools integrated in Mopsihttp://cs.uef.fi/mopsi/ (accessed on 24 November 2021)
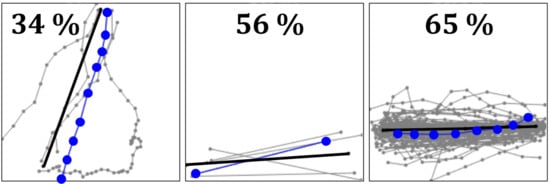
5. Results
- HC-SIM performs best with the training data.
- The choice of distance function has only a minor effect.
- The results of medoid are significantly worse than the baseline averaging [7].
6. Detailed Analysis
6.1. Noise
6.2. Re-Ordering and Outlier Removal
6.3. Normalizing
6.4. Size of Sets
6.5. Number of Points
7. Conclusions
- Accuracy of medoid is clearly inferior to the best averaging heuristics (baseline).
- Contrary to expectations, medoid is vulnerable to noise.
- Medoid tends to select short segments.
- Medoid copies the (sometimes unwanted) properties of the original trajectory.
- It is slow (averaging of all sets takes >1 h).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hautamäki, V.; Nykanen, P.; Fränti, P. Time-series clustering by approximate prototypes. In Proceedings of the International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Buchin, K.; Driemel, A.; van de L’Isle, N.; Nusser, A. Klcluster: Center-based Clustering of Trajectories. In Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (SIGSPATIAL ’19), Chicago, IL, USA, 5–8 November 2019; pp. 496–499. [Google Scholar]
- Biagioni, J.; Eriksson, J. Inferring road maps from global positioning system traces: Survey and comparative evaluation. Transp. Res. Rec. 2012, 2291, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Karagiorgou, S.; Pfoser, D.; Wenk, C. A comparison and evaluation of map construction algorithms using vehicle tracking data. GeoInformatica 2015, 19, 601–632. [Google Scholar] [CrossRef] [Green Version]
- Mariescu-Istodor, R.; Fränti, P. Grid-based method for GPS route analysis for retrieval. ACM Trans. Spat. Algorithms Syst. (TSAS) 2017, 3, 8. [Google Scholar] [CrossRef]
- Jain, B.J.; Schultz, D. Sufficient conditions for the existence of a sample mean of time series under dynamic time warping. Ann. Math. Artif. Intell. 2020, 88, 313–346. [Google Scholar] [CrossRef]
- Fränti, P.; Mariescu-Istodor, R. Averaging GPS segments competition 2019. Pattern Recognit. 2021, 112, 107730. [Google Scholar] [CrossRef]
- Estivill-Castrol, V.; Murray, A.T. Discovering associations in spatial data—An efficient medoid based approach. In Research and Development in Knowledge Discovery and Data Mining; Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1394. [Google Scholar]
- Mukherjee, A.; Basu, T. A medoid-based weighting scheme for nearest-neighbor decision rule toward effective text categorization. SN Appl. Sci. 2020, 2, 1–9. [Google Scholar] [CrossRef]
- Fränti, P.; Yang, J. Medoid-Shift for Noise Removal to Improve Clustering. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 3–7 June 2018; Springer: Cham, Switzerland, 2018; pp. 604–614. [Google Scholar]
- Park, H.-S.; Jun, C.-H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2019, 36, 3336–3341. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]
- Wagstaff, K.; Cardie, C.; Rogers, S.; Schroedl, S. Constrained k-means clustering with background knowledge. In Proceedings of the International Conference on Machine Learning (ICML), Williamstown, MA, USA, 28 June–1 July 2001; Volume 1, pp. 577–584. [Google Scholar]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1999, 29, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Van der Laan, M.; Pollard, K.; Bryan, J. A new partitioning around medoids algorithm. J. Stat. Comput. Simul. 2003, 73, 575–584. [Google Scholar] [CrossRef] [Green Version]
- Fränti, P.; Sieranoja, S. How much can k-means be improved by using better initialization and repeats? Pattern Recognit. 2019, 93, 95–112. [Google Scholar] [CrossRef]
- Fränti, P. Efficiency of random swap clustering. J. Big Data 2018, 5, 13. [Google Scholar] [CrossRef]
- Rezaei, M.; Fränti, P. Can the Number of Clusters Be Determined by External Indices? IEEE Access 2020, 8, 89239–89257. [Google Scholar] [CrossRef]
- Yang, J.; Rahardja, S.; Fränti, P. Mean-shift outlier detection and filtering. Pattern Recognit. 2021, 115, 107874. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. K-means properties on six clustering benchmark datasets. Appl. Intell. 2018, 48, 4743–4759. [Google Scholar] [CrossRef]
- Schultz, D.; Jain, B. Nonsmooth analysis and subgradient methods for averaging in dynamic time warping spaces. Pattern Recognit. 2018, 74, 340–358. [Google Scholar] [CrossRef] [Green Version]
- Brill, M.; Fluschnik, T.; Froese, V.; Jain, B.; Niedermeier, R.; Schultz, D. Exact mean computation in dynamic time warping spaces. Data Min. Knowl. Discov. 2019, 33, 252–291. [Google Scholar] [CrossRef] [Green Version]
- Schroedl, S.; Wagstaff, K.; Rogers, S.; Langley, P.; Wilson, C. Mining GPS traces for map refinement. Data Min. Knowl. Discov. 2004, 9, 59–87. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Mariescu-Istodor, R.; Fränti, P. Cellnet: Inferring road networks from GPS trajectories. ACM Trans. Spat. Algorithms Syst. (TSAS) 2018, 4, 1–22. [Google Scholar] [CrossRef]
- Fathi, A.; Krumm, J. Detecting road intersections from GPS traces. In Proceedings of the International Conference on Geographic Information Science, Zurich, Switzerland, 14–17 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 56–69. [Google Scholar]
- Etienne, L.; Devogele, T.; Buchin, M.; McArdle, G. Trajectory Box Plot: A new pattern to summarize movements. Int. J. Geogr. Inf. Sci. 2016, 30, 835–853. [Google Scholar] [CrossRef]
- Marteau, P.F. Times Series Averaging and Denoising from a Probabilistic Perspective on Time–Elastic Kernels. Int. J. Appl. Math. Comput. Sci. 2019, 29, 375–392. [Google Scholar] [CrossRef] [Green Version]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica 1973, 10, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Drezner, Z.; Klamroth, K.; Schöbel, A.; Wesolowsky, G.O. The weber problem. In Facility Location: Applications and Theory; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Mariescu-Istodor, R.; Fränti, P. Three rapid methods for averaging GPS segments. Appl. Sci. 2019, 9, 4899. [Google Scholar] [CrossRef] [Green Version]
- Trasarti, R.; Guidotti, R.; Monreale, A.; Giannotti, F. Myway: Location prediction via mobility profiling. Inf. Syst. 2017, 64, 350–367. [Google Scholar] [CrossRef]
- Vlachos, M.; Gunopulos, D.; Kollios, G. Robust similarity measures for mobile object trajectories. In Proceedings of the 13th IEEE International Workshop on Database and Expert Systems Applications (DEXA’02), Aix-en-Provence, France, 2–6 September 2002; pp. 721–726. [Google Scholar]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MD, USA, 14–16 June 2005; pp. 491–502. [Google Scholar]
- Rockafellar, T.R.; Wets, R.J.-B. Variational Analysis; Springer: Berlin/Heidelberg, Germany, 2009; Volume 317. [Google Scholar]
- Chen, L.; Ng, R. On the marriage of lp-norms and edit distance. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004; Volume 30, pp. 792–803. [Google Scholar]
- Zheng, Y.; Zhou, X. Computing with Spatial Trajectories; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 6th ed.; Academic Press: San Diego, CA, USA, 2000; pp. 1114–1125. [Google Scholar]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance. In Technical Report CD-TR 94/64; Christian Doppler Laboratory for Expert Systems, TU Vienna: Vienna, Austria, 1994; pp. 636–637. [Google Scholar]
- Nie, P.; Chen, Z.; Xia, N.; Huang, Q.; Li, F. Trajectory similarity analysis with the weight of direction and k-neighborhood for AIS data. ISPRS Int. J. Geo-Inf. 2021, 10, 757. [Google Scholar] [CrossRef]
- Wang, H.; Su, H.; Zheng, K.; Sadiq, S.; Zhou, X. An effectiveness study on trajectory similarity measures. In Proceedings of the Twenty-Fourth Australasian Database Conference, Adelaide, Australia, 29 January–1 February 2013; Volume 137, pp. 13–22. [Google Scholar]
- Yujian, L.; Bo, L. A normalized Levenshtein distance metric. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1091–1095. [Google Scholar] [CrossRef]
- Müller, M. Dynamic time warping. In Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; pp. 69–84. [Google Scholar]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef] [Green Version]
- Waga, K.; Tabarcea, A.; Chen, M.; Fränti, P. Detecting movement type by route segmentation and classification. In Proceedings of the 8th International Conference on Collaborative Computing: Networking, Applications and Worksharing (CollaborateCom), Pittsburgh, PA, USA, 14–17 October 2012. [Google Scholar]
- Chen, M.; Xu, M.; Fränti, P. A fast O(N) multi-resolution polygonal approximation algorithm for GPS trajectory simplification. IEEE Trans. Image Process. 2012, 21, 2770–2785. [Google Scholar] [CrossRef]
- Mariescu-Istodor, R.; Fränti, P. Gesture input for GPS route search. In Proceedings of the Joint International Workshop on Structural, Syntactic, and Statistical Pattern Recognition (S+SSPR 2016), Merida, Mexico, 29 November–2 December 2016; pp. 439–449. [Google Scholar]














| Measure | Sampling Rate | Noise | Point Shifting | Reference | Human Score | ||
|---|---|---|---|---|---|---|---|
| Increase | Decrease | Random | Sync. | ||||
| HC-SIM | Robust | Robust | Fair | Fair | Fair | [7] | 0.84 |
| C-SIM | Robust | Robust | Fair | Fair | Fair | [5] | 0.72 |
| IRD | Robust | Robust | Fair | Fair | Fair | [33] | 0.52 |
| LCSS | Sensitive | Fair | Sensitive | Fair | Fair | [34] | 0.45 |
| EDR | Sensitive | Fair | Sensitive | Fair | Fair | [35] | 0.37 |
| Hausdorff | Sensitive | Sensitive | Sensitive | Sensitive | Fair | [36] | 0.32 |
| ERP | Sensitive | Fair | Sensitive | Fair | Fair | [37] | 0.21 |
| DTW | Robust | Sensitive | Sensitive | Sensitive | Sensitive | [38] | 0.11 |
| Euclidean | Sensitive | Sensitive | Sensitive | Robust | Robust | [39] | 0.09 |
| Discrete Fréchet | Sensitive | Sensitive | Sensitive | Sensitive | Fair | [40] | 0.05 |
| Set | Number of Sets | Segments per Set (av.) | Points per Segment (av.) | Segment Length (av.) |
|---|---|---|---|---|
| Joensuu 2015 | 227 | 4.16 | 22.84 | 1.01 km |
| Chicago | 227 | 84.63 | 4.61 | 0.76 km |
| Berlin | 625 | 6.97 | 2.08 | 0.98 km |
| Athens | 614 | 3.30 | 2.46 | 0.88 km |
| Measure | Training | Testing | Testing | Testing |
|---|---|---|---|---|
| No Pre-Processing | +Re-Ordering | +Outlier Removal | ||
| HC-SIM | 59.9% | 55.7% | 55.7% (0.0) | 55.9% (+0.2) |
| IRD | 59.1% | 55.3% | 55.6% (+0.3) | 55.9% (+0.3) |
| Hausdorff | 59.0% | 55.3% | 55.3% (0.0) | 55.0% (−0.3) |
| Fréchet | 58.6% | 54.7% | 55.3% (+0.6) | 54.9% (−0.4) |
| EDR | 58.4% | 54.6% | 54.6% (0.0) | 55.7% (+1.1) |
| DTW | 57.2% | 54.2% | 54.1% (−0.1) | 55.3% (+1.2) |
| FastDTW | 57.1% | 54.4% | 54.1% (−0.3) | 54.8% (+0.7) |
| C-SIM | 57.1% | 55.3% | 55.3% (0.0) | 56.0% (+0.7) |
| ERP | 57.0% | 54.4% | 54.5% (+0.1) | 54.6% (+0.1) |
| LCSS | 56.9% | 54.4% | 54.6% (+0.2) | 55.7% (+1.1) |
| Euclidean | 56.7% | 54.1% | 54.9% (+0.8) | 55.1% (+0.2) |
| Average | 57.9% | 54.8% | 54.9% (+0.1) | 55.4% (+0.5) |
| No Pre-Processing | |||||
| Measure | Number of Sets with Scores | ||||
| <30% | 30–40% | 40–70% | 70–90% | >90% | |
| HC-SIM | 102 | 120 | 434 | 211 | 34 |
| IRD | 93 | 120 | 474 | 169 | 45 |
| Hausdorff | 98 | 125 | 447 | 179 | 52 |
| Fréchet | 100 | 129 | 456 | 170 | 46 |
| EDR | 112 | 122 | 446 | 172 | 49 |
| DTW | 108 | 130 | 450 | 174 | 39 |
| FastDTW | 101 | 131 | 457 | 166 | 46 |
| C-SIM | 114 | 111 | 437 | 199 | 40 |
| ERP | 100 | 130 | 459 | 169 | 43 |
| LCSS | 113 | 131 | 438 | 171 | 48 |
| Euclidean | 107 | 126 | 459 | 173 | 36 |
| Re-ordered | |||||
| Measure | Number of Sets with Scores | ||||
| <30% | 30–40% | 40–70% | 70–90% | >90% | |
| HC-SIM | 102 | 119 | 436 | 211 | 33 |
| IRD | 90 | 117 | 471 | 182 | 41 |
| Hausdorff | 98 | 125 | 447 | 179 | 52 |
| Fréchet | 101 | 124 | 447 | 178 | 51 |
| EDR | 114 | 125 | 439 | 169 | 54 |
| DTW | 115 | 113 | 466 | 165 | 42 |
| FastDTW | 110 | 119 | 465 | 171 | 36 |
| C-SIM | 115 | 110 | 435 | 200 | 41 |
| ERP | 101 | 120 | 472 | 166 | 42 |
| LCSS | 113 | 126 | 438 | 172 | 52 |
| Euclidean | 103 | 118 | 457 | 184 | 39 |
| Re-ordered and outlier removal | |||||
| Measure | Number of Sets with Scores | ||||
| <30% | 30–40% | 40–70% | 70–90% | >90% | |
| HC-SIM | 95 | 117 | 441 | 210 | 38 |
| IRD | 96 | 112 | 460 | 181 | 52 |
| Hausdorff | 102 | 116 | 463 | 176 | 44 |
| Fréchet | 101 | 117 | 462 | 179 | 42 |
| EDR | 101 | 119 | 437 | 196 | 48 |
| DTW | 103 | 109 | 469 | 171 | 49 |
| FastDTW | 111 | 125 | 436 | 186 | 43 |
| C-SIM | 96 | 115 | 437 | 214 | 39 |
| ERP | 106 | 116 | 460 | 175 | 44 |
| LCSS | 100 | 120 | 437 | 198 | 46 |
| Euclidean | 98 | 121 | 459 | 182 | 41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jimoh, B.; Mariescu-Istodor, R.; Fränti, P. Is Medoid Suitable for Averaging GPS Trajectories? ISPRS Int. J. Geo-Inf. 2022, 11, 133. https://doi.org/10.3390/ijgi11020133
Jimoh B, Mariescu-Istodor R, Fränti P. Is Medoid Suitable for Averaging GPS Trajectories? ISPRS International Journal of Geo-Information. 2022; 11(2):133. https://doi.org/10.3390/ijgi11020133
Chicago/Turabian StyleJimoh, Biliaminu, Radu Mariescu-Istodor, and Pasi Fränti. 2022. "Is Medoid Suitable for Averaging GPS Trajectories?" ISPRS International Journal of Geo-Information 11, no. 2: 133. https://doi.org/10.3390/ijgi11020133
APA StyleJimoh, B., Mariescu-Istodor, R., & Fränti, P. (2022). Is Medoid Suitable for Averaging GPS Trajectories? ISPRS International Journal of Geo-Information, 11(2), 133. https://doi.org/10.3390/ijgi11020133