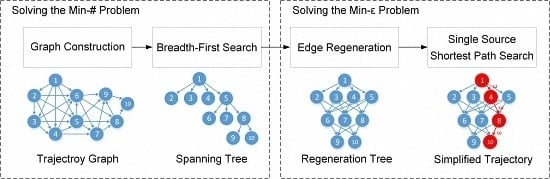
This section first describes three common datasets and three algorithms for comparison, then evaluates three aspects, namely error metrics, time cost, and delay/gap analysis. Finally, the results are discussed and the performance of the proposed algorithms is summarized.
5.2. Evaluation Based on Error Metrics
Error metrics measure the compression effectiveness. Generally, a smaller approximation error indicates a better compression result. This section compares five algorithms across multiple metrics including average
SED, max
SED, median
SED, and average
ISSED. The abbreviation and calculation formula of the above four kinds of error metrics are listed in
Table 4.
Experiment settings. A trajectory of 3747 points in Mopsi is selected. Error metrics are measured under different compression rates. Ten compression rates are chosen by setting different distance thresholds.
Average SED. Generally, smaller average
SED error indicates better compression results. As shown in
Figure 14a, the average
SED error increases as the compression rate grows. OPTTS has the smallest error at each compression rate, followed by OLTS. The average
SED error of OLTS is reduced by 40.8%, while the
SED error of OPTTS is reduced by 45.6%.
Max SED. Max
SED error is used to evaluate the stability of TS algorithms. The gentler the upward trend of the curve, the more stable of the algorithm.
Figure 14b shows that OPTTS and OLTS have stable performance under different compression rates. The maximum value is 3~4 times of the average value. However, OPW, D-P, and MRPA have large fluctuation as the compression rates increase. The maximum values have a sudden surge to 6~8 times of the average values.
Median SED. Abnormal large value of
SED may increase the average value, so it is insufficient to measure the performance only by average
SED error. Median
SED error is chosen as the auxiliary condition of average
SED. As shown in
Figure 14c, the situation of the median values are similar to the average values. OPTTS still has the smallest error, followed by OLTS.
Average ISSED. Average
ISSED measures the overall approximation error of the compressed trajectory, which is also the optimization goal.
Figure 14d shows that OPTTS has the lowest average
LISSED error, followed by OLTS. OPTTS reduces the
LISSED error by 82.2% compared to traditional algorithms, while OLTS reduces the error by 77.1%.
Average SEDs on different datasets. Average
SED error is used to evaluate the robustness of the algorithms under different datasets. Three representative trajectories are selected respectively from Geolife, Mopsi, and Movebank datasets. Average
SED error is calculated with fixed compression ratio
. For better comparison, max-min normalization is utilized to unify different datasets to the same reference system.
Figure 14e shows that OPTTS and OLTS perform relatively stable on all datasets, while OPW, D-P, and MRPA show a large fluctuation.
Visualization of Compression Result. The approximation error represents the deviation between the compressed and the original trajectory. It can be seen intuitively from the graphical representation of trajectories how large the difference is.
Figure 15 shows the visualization of the compressed and the original trajectories by different algorithms. The same trajectory in the evaluation of error metrics is selected and the compression ratio is set to 100. In
Figure 15a–d, the blue line always represents the original trajectory and the red one represents the result of OPTTS. The green lines respectively show the results of OLTS, MRPA, OPW, and D-P. It can be seen from
Figure 15d that the compressed trajectory of D-P has the largest deviation, and the result of OPTTS is the most accurate representation of the original trajectory.
Experiment settings. Time cost is measured through two aspects, namely the number of points and compression rate. First, a trajectory from Geolife is selected and compression is executed every 5000 points from 5000 to 40,000 with a fixed rate . When exploring the relationship with the compression rate, a trajectory from Mopsi is chosen and simplification is made at 10 different compression rates with a fixed number of points. All algorithms were implemented in C++ and run on a Windows (64 bit) platform with a 2.50 GHz i7 CPU and 8 GB RAM.
Effect of number of points. As illustrated in
Figure 16a, time costs of all algorithms show an increasing trend with the growth of points. OLTS is 32.2% faster than the traditional online algorithm OPW, even 40.3% faster than offline algorithm MRPA. While OPTTS is slower compared to other algorithms.
Effect of compression rates. As shown in
Figure 16b, time costs of D-P, OPW, and OPTTS do not change with compression ratio, while MRPA and OLTS show an upward trend. When the compression ratio is less than 20, OLTS runs ahead of the D-P, OPW, and OPTTS. OLTS is faster than MRPA when the compression ratio is higher than 20.
5.3. Evaluation Based on Delay/Gap Analysis
Visualization of delay and gap. Delay and gap are important features of OLTS. Three trajectories from Mopsi, Geolife, and Movebank with 3273 points are simplified on a fixed compression rate
. The relationship between input index and output index is shown in
Figure 17a. The Movebank dataset (red line) has the largest delay and gap. When the 2181st point is imported, the OLTS outputs the 2078th point. From the 2182nd to the 2457th point, there is no output of the algorithm. Until the input of the 2458th point, the 2160th point is output. Therefore, Delay = 2458 − 2181 and Gap = 2458 − 2160.
Average Delay. The relationship between delay and compression rate is shown in
Figure 17b. The average delay is approximately equal to the compression rate in all datasets. Therefore, OLTS can guarantee a stable delay in various datasets.
Average Gap. The association between compression rate and average gap is shown in
Figure 17c. Generally, OLTS’s gap becomes larger as the compression rate increases. The average gap of the Movebank dataset is the largest, followed by Geolife and Mopsi.
5.4. Discussion
Effectiveness analysis. First, OPTTS has achieved the smallest result over all error metrics. OPTTS utilizes breadth-first spanning-regeneration tree and shortest path search to solve both min-# and min-ε problem and thus achieves the optimal solution. The approximation error of OLTS is slightly higher than OPTTS. Since OLTS extends the basic framework of OPTTS and utilizes a stopping criterion to speed up the construction of spanning tree, which leads to a near optimal result. However, D-P, OPW, and MRPA uses greedy strategy to improve efficiency, but the compression error is large. As is shown in
Figure 15d, the green line representing the result of D-P has large deviation from the original trajectory. The performance of D-P may be unacceptable to some applications where the trajectory should be compressed as accurate as possible. For example, in some navigation applications, if the user’s trajectories compressed by D-P have a large approximation error, it may lead to deviation from the road map which is misleading. Secondly, OPTTS and OLTS have stable max
SED errors since they use global optimal methods. However, D-P, OPW, and MRPA have abnormally large max
SED at some parts of trajectory, due to the inappropriate selection of local optimization conditions. Finally, OPTTS and OLTS can achieve stable performance in all datasets. The influence of different features of the three datasets is reduced by the selection of an optimal method.
Time complexity analysis. Time complexity from theoretical derivation is summarized in
Table 5. In the efficiency evaluation, D-P is the fastest among five algorithms, followed by OLTS and MRPA. D-P is heuristic-based and does not suffer from high complexity, while OPTTS utilizes optimization method during the construction of a breadth-first spanning regeneration tree, which is time consuming. However, the time cost of OPTTS is still acceptable to most offline applications, where the time cost is not considered as important as the performance of the compression. As is shown in
Figure 15a, the time cost of OPTTS to a 1200 point trajectory is around 100 ms. It can be calculated that the total time cost for compressing all 14,638 trajectories in Geolife is about 24 min, which is tolerable. Thus, the improvement of compression effectiveness of OPTTS overwhelms the loss of computing efficiency. Furthermore, the time complexity of OLTS and MRPA is positively correlated with
N/M, so the time cost rises as the increasing of compression rate. While OPTTS, OPW and D-P are only related to the number of points.
Delay and gap analysis. The proposed OLTS have uncertain delay and gap, introduced by the incremental construction of the breadth-first spanning tree and real-time output. The gap is correlated with the distance between
and
, and delay represents the number of nodes in each layer of the spanning tree, that is
. First, local delay and gap may be influenced by the moving status of the object. As illustrated in
Figure 17a, delay and gap have abnormally large values at some parts of the trajectory. This is because that the osprey may maintain a direct flight status for a long time. Secondly, average delay is approximately equal to compression rate. Because delay in OLTS represents the number of nodes in each layer of the spanning tree, which is equal to the compression rate. Finally, as illustrated in
Figure 17c, the gap is 3~5 times of the compression rate, because the gap is related to the distance between
and
, which is bounded by
. Therefore, the gap should be in proportion to
in theory.