Effective Identification of Terrain Positions from Gridded DEM Data Using Multimodal Classification Integration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Definition Scheme of Terrain Positions
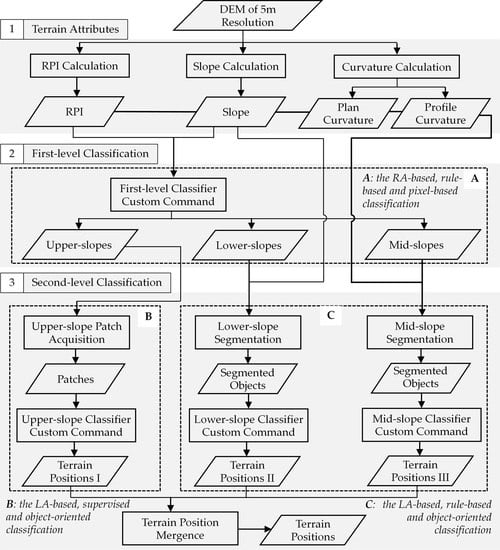
2.3. Methodology for Classifying Terrain Positions
2.3.1. Calculation of Terrain Attributes
2.3.2. Determining the First-Level Parameters
2.3.3. Determining the Second-Level Parameters
2.4. Rationality Assessment of Terrain Position Classification
3. Results and Discussion
3.1. First-Level Classification
3.2. Second-Level Classification
3.3. Rationality Analysis of Terrain Positions
4. Conclusions
- (1)
- The positional relationship of terrain positions has a good consistency with their geographic meanings. The inter-class difference of terrain positions is relatively large, and the intra-class variances are relatively small. Both above viewpoints indicate that terrain positions are consistent with the actual topography from both overall and local perspectives.
- (2)
- The two-level definition scheme effectively complies with the geographical cognition and topographic features of terrain positions from different levels, and sufficiently matches with the multimodal classification.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Skidmore, A.K. Terrain position as mapped from a gridded digital elevation model. Int. J. Geogr. Inf. Syst. 1990, 4, 33–49. [Google Scholar] [CrossRef]
- Schmidt, J.; Hewitt, A. Fuzzy land element classification from DTMs based on geometry and terrain position. Geoderma 2004, 121, 243–256. [Google Scholar] [CrossRef]
- Minar, J.; Evans, I.S. Elementary forms for land surface segmentation: The theoretical basis of terrain analysis and geomorphological mapping. Geomorphology 2008, 95, 236–259. [Google Scholar] [CrossRef]
- MacMillan, R.A.; Shary, P.A. Landforms and landform elements in geomorphometry. In Geomorphometry: Concepts, Software, Applications; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 227–254. [Google Scholar]
- Matsuura, T.; Aniya, M. Automated segmentation of hillslope profiles across ridges and valleys using a digital elevation model. Geomorphology 2012, 177–178, 167–177. [Google Scholar] [CrossRef]
- Bishop, M.P.; James, L.A.; Shroder, J.F.; Walsh, S.J. Geospatial technologies and digital geomorphological mapping: Concepts, issues and research. Geomorphology 2012, 137, 5–26. [Google Scholar] [CrossRef]
- Liu, X.J.; Tang, G.A.; Yang, J.Y.; Shen, Z.; Pan, T. Simulating evolution of a loess gully head with cellular automata. Chin. Geogr. Sci. 2015, 25, 765–774. [Google Scholar] [CrossRef]
- Speight, J.G. Landform. In Australian Soil and Land Survey: Field Handbook, 2nd ed.; Mcdonald, R.C., Isbell, R.F., Speight, J.G., Walker, J., Hopkins, M.S., Eds.; Inkata Press: Melbourne, Australia, 1990; pp. 9–57. [Google Scholar]
- Qin, C.Z.; Zhu, A.X.; Qiu, W.L.; Lu, Y.J.; Li, B.L.; Pei, T. Mapping soil organic matter in small low-relief catchments using fuzzy slope position information. Geoderma 2012, 171–172, 64–74. [Google Scholar] [CrossRef]
- Behrens, T.; Schmidt, K.; Ramirez-Lopez, L.; Gallant, J.; Zhu, A.X.; Scholten, T. Hyper-scale digital soil mapping and soil formation analysis. Geoderma 2014, 213, 578–588. [Google Scholar] [CrossRef]
- Pennock, D.J. Terrain attributes, landform segmentation, and soil redistribution. Soil Tillage Res. 2003, 69, 15–26. [Google Scholar] [CrossRef]
- Schwanghart, W.; Groom, G.; Kuhn, N.J.; Heckrath, G. Flow network derivation from a high resolution DEM in a low relief, agrarian landscape. Earth Surf. Proc. Landf. 2013, 38, 1576–1586. [Google Scholar] [CrossRef]
- Wood, S.W.; Murphy, B.P.; Bowman, D.M.J.S. Firescape ecology: How topography determines the contrasting distribution of fire and rain forest in the south-west of the Tasmanian Wilderness World Heritage Area. J. Biogeogr. 2011, 38, 1807–1820. [Google Scholar] [CrossRef]
- Pennock, D.J.; Zebarth, B.J.; De Jong, E. Landform classification and soil distribution in hummocky terrain, Saskatchewan, Canada. Geoderma 1987, 40, 297–315. [Google Scholar] [CrossRef]
- Dikau, R.; Brabb, E.; Mark, R.K.; Pike, R.J. Morphometric landform analysis of New Mexico. Z. Geomorphol. Suppl. 1995, 101, 109–126. [Google Scholar]
- MacMillan, R.A.; Pettapiece, W.W.; Nolan, S.C.; Goddard, T.W. A generic procedure for automatically segmenting landforms into landform elements using DEMs, heuristic rules and fuzzy logic. Fuzzy Sets Syst. 2000, 113, 81–109. [Google Scholar] [CrossRef]
- Wieczorek, M.; Migoń, P. Automatic relief classification versus expert and field based landform classification for the medium-altitude mountain range, the Sudetes, SW Poland. Geomorphology 2014, 206, 133–146. [Google Scholar] [CrossRef]
- Weiss, A.D. Topographic position and landforms analysis. In Proceedings of the ESRI User Conference, San Diego, CA, USA, 9–13 July 2001. [Google Scholar]
- Jasiewicz, J.; Stepinski, T.F. Geomorphons: A pattern recognition approach to classification and mapping of landforms. Geomorphology 2013, 182, 147–156. [Google Scholar] [CrossRef]
- Brown, D.G.; Lusch, D.P.; Duda, K.A. Supervised classification of types of glaciated landscapes using digital elevation data. Geomorphology 1998, 21, 233–250. [Google Scholar] [CrossRef]
- Prima, O.D.A.; Echigo, A.; Yokoyama, R.; Yoshida, T. Supervised landform classification of Northeast Honshu from DEM-derived thematic maps. Geomorphology 2006, 78, 373–386. [Google Scholar] [CrossRef]
- Wei, Z.; He, H.; Hao, H.; Gao, W. Automated mapping of landforms through the application of supervised classification to lidAR-derived DEMs and the identification of earthquake ruptures. Int. J. Remote Sens. 2017, 38, 7196–7219. [Google Scholar] [CrossRef]
- Ventura, S.J.; Irvin, B.J. Automated landform classification methods for soil-landscape studies. In Terrain Analysis: Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley & Sons: New York, NY, USA, 2000; pp. 267–294. [Google Scholar]
- Iwahashi, J.; Pike, R.J. Automated classifications of topography from DEMs by an unsupervised nested-means algorithm and a three-part geometric signature. Geomorphology 2007, 86, 409–440. [Google Scholar] [CrossRef]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- D’Oleire-Oltmanns, S.; Eisank, C.; Drăguţ, L.; Blaschke, T. An object-based workflow to extract landforms at multiple scales from two distinct data types. IEEE Geosci. Remote Sens. Lett. 2013, 10, 947–951. [Google Scholar] [CrossRef]
- Pedersen, G.B.M. Semi-automatic classification of glaciovolcanic landforms: An object-based mapping approach based on geomorphometry. J. Volcanol. Geotherm. Res. 2016, 311, 29–40. [Google Scholar] [CrossRef]
- Schneevoigt, N.J.; van der Linden, S.; Thamm, H.P.; Schrott, L. Detecting Alpine landforms from remotely sensed imagery. A pilot study in the Bavarian Alps. Geomorphology 2008, 93, 104–119. [Google Scholar] [CrossRef]
- Kramm, T.; Hoffmeister, D.; Curdt, C.; Maleki, S.; Khormali, F.; Kehl, M. Accuracy assessment of landform classification approaches on different spatial scales for the Iranian loess plateau. ISPRS Int. J. Geo-Inf. 2017, 6, 366. [Google Scholar] [CrossRef]
- Gruber, F.E.; Baruck, J.; Geitner, C. Algorithms vs. surveyors: A comparison of automated landform delineations and surveyed topographic positions from soil mapping in an Alpine environment. Geoderma 2017, 308, 9–25. [Google Scholar] [CrossRef]
- Qin, C.Z.; Zhu, A.X.; Shi, X.; Li, B.L.; Pei, T.; Zhou, C.H. Quantification of spatial gradation of slope positions. Geomorphology 2009, 110, 152–161. [Google Scholar] [CrossRef] [Green Version]
- Guo, P.T.; Wu, W.; Sheng, Q.K.; Li, M.F.; Liu, H.B.; Wang, Z.Y. Prediction of soil organic matter using artificial neural network and topographic indicators in hilly areas. Nutr. Cycl. Agroecosyst. 2013, 95, 333–344. [Google Scholar] [CrossRef]
- Zeng, C.; Yang, L.; Zhu, A.X.; Rossiter, D.G.; Liu, J.; Liu, J.Z.; Qin, C.Z.; Wang, D.S. Mapping soil organic matter concentration at different scales using a mixed geographically weighted regression method. Geoderma 2016, 281, 69–82. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.J.; Tang, G.A.; Li, F.Y.; Zhang, L. Snake model for the extraction of loess shoulder-line from DEMs. J. Mt. Sci. 2014, 11, 1552–1559. [Google Scholar] [CrossRef]
- Rueda, A.; Noguera, J.M.; Martínez-Cruz, C. A flooding algorithm for extracting drainage networks from unprocessed digital elevation models. Comput. Geosci. 2013, 59, 116–123. [Google Scholar] [CrossRef]
- Lucian, D.; Dirk, T.; Shaun, R.L. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar]
- Saadat, H.; Bonnell, R.; Sharifi, F.; Mehuys, G.; Namdar, M.; Ale-Ebrahim, S. Landform classification from a digital elevation model and satellite imagery. Geomorphology 2008, 100, 453–464. [Google Scholar] [CrossRef]
- Ruhe, R.V. Quaternary Landscapes in IOWA, 1st ed.; Iowa State University Press: Ames, IA, USA, 1969. [Google Scholar]
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. B 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Qin, C.Z.; Zhu, A.X.; Pei, T.; Li, B.L.; Scholten, T.; Behrens, T.; Zhou, C.H. An approach to computing topographic wetness index based on maximum downslope gradient. Precis. Agric. 2011, 12, 32–43. [Google Scholar] [CrossRef]
- Liang, W.L.; Chan, M.C. Spatial and temporal variations in the effects of soil depth and topographic wetness index of bedrock topography on subsurface saturation generation in a steep natural forested headwater catchment. J. Hydrol. 2017, 546, 405–418. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. (Eds.) Second Topographic Attributes. In Terrain Analysis: Principles and Applications; John Wiley & Sons: New York, NY, USA, 2000; pp. 106–113. [Google Scholar]










| Terrain Position | RPI | Curvature (1/m) | Slope (°) | Description | ||
|---|---|---|---|---|---|---|
| First Level | Second Level | Plan | Profile | |||
| Upper slope | Ridge | [β, 1] | ND | ND | ND | Mostly with large covering area and strip-shaped cross-sections |
| Hillock | ND | ND | ND | Mainly with small covering area and short cross-sections | ||
| Mid slope | Shoulder | (α, β) | ≤0 | >0 | ND | Convex element |
| Nose slope | >0 | >0 | ND | Convex slope | ||
| Head slope | <0 | <0 | ND | Concave slope | ||
| Back slope | ≥0 | <0 | ND | Concave element | ||
| Side slope | (−0.2,0.2) | (−0.2,0.2) | ND | Rectilinear slope | ||
| Lower slope | Valley | [0, α] | ND | ND | >2 | Lower element receiving water |
| Lower flat | ND | ND | ≤2 | Flat element in the lower topographic position | ||
| Terrain Attribute | Algorithm | Implementation |
|---|---|---|
| Slope | Third-order finite difference weighted by reciprocal of squared distance | ArcGIS software |
| Plan and profile curvature | Fourth-order polynomial | ArcGIS software |
| Negative terrain | Algorithm from Yan et al. [34] | Programming in C++ with Matlab |
| Ridge | D8 algorithm | ArcGIS software |
| Valley | Algorithm from Rueda et al. [35] | Programming in C++ with GDAL |
| Terrain hillshade | Single-directional hillshade algorithm | ArcGIS software |
| Shoulder | Nose Slope | Head Slope | Back Slope | Side Slope | Lower Flat | Valley | Ridge | Hillock | |
|---|---|---|---|---|---|---|---|---|---|
| RPI | 0.45 | 0.32 | 0.61 | 0.55 | 0.56 | 0.00 | 0.00 | 1.00 | 1.00 |
| Elevation (m) | 1003.71 | 981.77 | 1013.72 | 1002.63 | 1008.39 | 891.93 | 938.77 | 1034.75 | 1016.87 |
| Method in this Paper | Drăguţ Method | ||||
|---|---|---|---|---|---|
| Terrain Position | Inter-Class Distance | Intra-Class Distance | Terrain Position | Inter-Class Distance | Intra-Class Distance |
| Ridge | 0.90 | 0.38 | Peak | 0.94 | 0.58 |
| Hillock | 1.06 | 0.76 | Steep slope | 1.05 | 0.36 |
| Shoulder | 0.77 | 0.36 | Shoulder | 0.88 | 0.17 |
| Side slope | 1.06 | 0.53 | Side slope | 0.97 | 1.22 |
| Nose slope | 0.80 | 0.20 | Nose slope | 0.85 | 0.55 |
| Head slope | 0.75 | 0.24 | Head slope | 0.93 | 0.30 |
| Back slope | 0.73 | 0.11 | Negative contact | 0.97 | 0.17 |
| Valley | 1.01 | 0.26 | Toe slope | 1.51 | 1.15 |
| Lower flat | 1.88 | 0.98 | Flat or gentle slope | 1.65 | 1.34 |
| Mean | 1.00 | 0.42 | Mean | 1.08 | 0.65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Ling, D.; Zhao, M.; Wang, C.; Liang, Q.; Liu, K. Effective Identification of Terrain Positions from Gridded DEM Data Using Multimodal Classification Integration. ISPRS Int. J. Geo-Inf. 2018, 7, 443. https://doi.org/10.3390/ijgi7110443
Jiang L, Ling D, Zhao M, Wang C, Liang Q, Liu K. Effective Identification of Terrain Positions from Gridded DEM Data Using Multimodal Classification Integration. ISPRS International Journal of Geo-Information. 2018; 7(11):443. https://doi.org/10.3390/ijgi7110443
Chicago/Turabian StyleJiang, Ling, Dequan Ling, Mingwei Zhao, Chun Wang, Qiuhua Liang, and Kai Liu. 2018. "Effective Identification of Terrain Positions from Gridded DEM Data Using Multimodal Classification Integration" ISPRS International Journal of Geo-Information 7, no. 11: 443. https://doi.org/10.3390/ijgi7110443
APA StyleJiang, L., Ling, D., Zhao, M., Wang, C., Liang, Q., & Liu, K. (2018). Effective Identification of Terrain Positions from Gridded DEM Data Using Multimodal Classification Integration. ISPRS International Journal of Geo-Information, 7(11), 443. https://doi.org/10.3390/ijgi7110443