Next Article in Journal
Air Pollution Dispersion Modelling Using Spatial Analyses
Next Article in Special Issue
Semi-Automatic Versus Manual Mapping of Cold-Water Coral Carbonate Mounds Located Offshore Norway
Previous Article in Journal
Checking the Consistency of Volunteered Phenological Observations While Analysing Their Synchrony
Previous Article in Special Issue
Integrating GEOBIA, Machine Learning, and Volunteered Geographic Information to Map Vegetation over Rooftops
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 7
Issue 12
10.3390/ijgi7120488
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparison of Independent Component Analysis, Principal Component Analysis, and Minimum Noise Fraction Transformation for Tree Species Classification Using APEX Hyperspectral Imagery

by
Zahra Dabiri
* and
Stefan Lang
Department of Geoinformatics-Z_GIS, University of Salzburg, 5020 Salzburg, Austria
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2018, 7(12), 488; https://doi.org/10.3390/ijgi7120488
Submission received: 2 October 2018 / Revised: 10 December 2018 / Accepted: 17 December 2018 / Published: 19 December 2018
(This article belongs to the Special Issue GEOBIA in a Changing World)
Browse Figures
Versions Notes

Abstract

:
Hyperspectral imagery provides detailed spectral information that can be used for tree species discrimination. The aim of this study is to assess spectral–spatial complexity reduction techniques for tree species classification using an airborne prism experiment (APEX) hyperspectral image. The methodology comprised the following main steps: (1) preprocessing (removing noisy bands) and masking out non-forested areas; (2) applying dimensionality reduction techniques, namely, independent component analysis (ICA), principal component analysis (PCA), and minimum noise fraction transformation (MNF), and stacking the selected dimensionality-reduced (DR) components to create new data cubes; (3) super-pixel segmentation on the original image and on each of the dimensionality-reduced data cubes; (4) tree species classification using a random forest (RF) classifier; and (5) accuracy assessment. The results revealed that tree species classification using the APEX hyperspectral imagery and DR data cubes yielded good results (with an overall accuracy of 80% for the APEX imagery and an overall accuracy of more than 90% for the DR data cubes). Among the classification results of the DR data cubes, the ICA-transformed components performed best, followed by the MNF-transformed components and the PCA-transformed components. The best class performance (according to producer’s and user’s accuracy) belonged to Picea abies and Salix alba. The other classes (Populus x (hybrid), Alnus incana, Fraxinus excelsior, and Quercus robur) performed differently depending on the different DR data cubes used as the input to the RF classifier.

Graphical Abstract

1. Introduction

The accurate classification of tree species is a key element for forest management, policy implementation, and the conservation sector for planning strategies and actions to address biodiversity loss [1,2]. During the last decades, remote sensing imagery has been extensively used to identify forest covers from broad categories (for example, deciduous against coniferous cover) to more detailed categories such as tree species classification [3]. Nevertheless, the accuracy of tree species classification is influenced by many factors, wherein the choice of the type of remote sensing imagery and the classification methodologies are the two main ones [4]. Hyperspectral imagery (also known as imaging spectroscopy) provides detailed spectral information, utilizing contiguous narrow spectral bands that can be used for tree species classification [4,5,6,7,8,9,10]. To perform tree species classification, one can link the spectral variability (spectral signature) of the features depicted on hyperspectral imagery to the biophysical characteristics of plants [11,12,13]. According to Harrison [14], the environmental monitoring of vegetation has widely used the visible (VIS; 400–700 nm) and the near and shortwave infrared (NIR: 700–1400 nm; SWIR: 1400–2500 nm) of the electromagnetic spectrum (EM). Each of these spectral regions provides different information; for instance, in the VIS, chlorophyll reflects in the green band (495–570 nm) and absorbs in the red and blue bands (620–750 nm and 450–495 nm, respectively). In the NIR, plants are strongly reflective, and their reflectance is driven by leaf thickness and internal morphology; few studies have utilized these features for species classification in the same sites and seasons [14,15,16].
However, analysis of hyperspectral imagery endures two major challenges: (a) the effect of spectral mixture, meaning that each pixel vector might measure multiple underlying materials, and (b) computational complexity occurring due to the high dimensionality of hyperspectral imagery (hypercube). This means that by increasing the dimensionality of the hypercube, the need for training samples will increase exponentially [17,18].
We coped with the first challenge—the problem of spectral mixture—by using high-spatial-resolution airborne hyperspectral imagery [19]. The high-spatial-resolution hyperspectral imagery allows us to conduct classification and mapping on a species level [20]. The high-spatial-resolution airborne hyperspectral imagery makes it possible to not only focus on spectral variability per pixel, but to also consider contextual and spatial information (such as relations to neighbor pixels, shape, size, etc.), and to extract a broad range of possible target features, at multiple scales [21,22,23,24,25,26,27].
The second challenge is related to computational complexity (also known as the curse of dimensionality, or Hughes phenomenon). According to the Hughes phenomenon, with an increase of the number of spectral bands, the number of training samples for training classifiers increases exponentially [17]; thus, it can significantly reduce classification accuracies. Therefore, instead of using the full set of spectral bands for data processing, one can apply dimensionality reduction techniques [18,28]. The process of dimensionality reduction is to transfer data from a high-order dimension to a low-order dimension. The main assumption is that a higher number of bands in hyperspectral imagery may cause information redundancy, meaning that the neighboring bands are highly correlated, and the information content of one band could be present in adjusted bands as well. Therefore, reducing the number of bands by applying dimensionality reduction techniques might reduce the computational complexity, without loss of information [29]. The dimensionality reduction techniques will be followed by information extraction such as performing classification or regression. According to Bajwa et al. and Thenkabail et al. [30,31], dimensionality reduction techniques can be grouped into two main categories: (1) supervised dimensionality reduction techniques, for example, estimation of correlation between features and ground data; and (2) unsupervised techniques, also known as blind signal separation (BSS), including principal component analysis (PCA) [32], minimum noise fraction (MNF) [33], and independent component analysis (ICA) transformations [34], as well as similarity measures, which measure the degree of similarity between pairs of bands or features [29].
PCA transformation is a multivariate method used for the reduction of spectral bands. The result of a PCA transformation is a group of projected bands (features, components) based on their variance. For example, performing the PCA transformation on hyperspectral imagery with numerous bands will result in few features, where the first component contains the highest variation and, hence, has the highest information content. The information content decreases as the number of the components increases. MNF transformation is equivalent to principal component transformation; however, instead of choosing new components to maximize variance, it chooses the new components to maximize the signal-to-noise ratio (SNR) [33]. The MNF transformation can be used to reduce the spectral dimensionality of hyperspectral imagery, to improve SNR, and to increase the speed of data processing [35,36,37]. Both the PCA and the MNF transformations are based on the calculation of the eigenvalue decomposition using a covariance matrix [38]. These two transformations assume the data to be normally distributed. The ICA transformation is an unsupervised feature extraction method, being applied to separate components, with the assumption that each band is a linear mixture of independent components. The main difference between the ICA transformation and the other two dimensionality reduction techniques is that in the ICA transformation, the assumption of normal distribution is not necessary [39].
Taking these considerations into account, the objective of this research is to assess the spectral and spatial dimensionality reduction of APEX hyperspectral imagery in the framework of geographic object-based image analysis (GEOBIA).

2. Materials and Methods

2.1. Study Area and Tree Species

The study area is located at the north-west of the city of Salzburg, over a length of 8.5 kilometers along the east side of the Salzach river (UL: N 47°56′12″/E 12°56′24″, LR: N 47°52′42″/E 12°59′21″), by the Austrian–German border (Figure 1). The average altitude is approximately 400 meters above sea level, and the average annual rainfall is 1200 mm, with a maximum rainfall in summer. The forested area is a mixture of dominant and plantation trees, water bodies and wetlands, and buildings and industrial areas. The plantation trees in the area comprise Picea abies and Populus x (hybrid). The more common native tree species are Fraxinus excelsior, Alnus incana, and Salix alba, whereas the less common native tree species are Acer pseudoplatus and Quercus robur. All these tree species except for Acer pseudoplatus were used in this study [40].

2.2. Data

Airborne prism experiment (APEX) hyperspectral imagery collected on 29 June 2011 was used. The APEX hyperspectral imagery has 288 bands and covers a spectral range of 413 nm to 2451 nm, with a spectral resolution of 10 nm and 2.5 m ground sample distance (GSD). The image contains two flight lines and two black stripes due to the presence of wires which were placed on the camera’s entry slit to observe spatial shifts. The image was delivered by VITO (Flemish Institute for Technological Research) in the geographic coordinate system lat. and long, WGS84. According to VITO, an atmospheric correction technique was performed by the experimental central data processing center (CDPC) [41], with the MODTRAN4 radiative transfer code, following the algorithm given in Hann et al., 1996 [42] and taking into account the in-flight determined central wavelengths for each pixel (column), which means it is a smile-aware atmospheric correction.

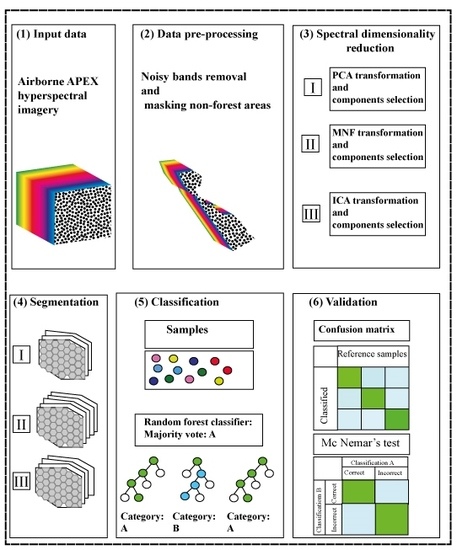
2.3. Methodology

The methodological workflow consisted of the following steps: (1) data preprocessing to remove noisy bands and to create a non-forest mask; (2) data processing, which involves applying dimensionality reduction techniques, and the generation of training and validation samples; (3) image segmentation on the dimensionality-reduced (DR) data cubes and the original APEX hyperspectral image; (4) data classification using the random forest (RF) algorithm for tree species classification; and (5) accuracy assessment (Figure 2).

2.4. Training and Validation Samples

Two field trips were done in summer 2017 and 2018, and 183 sample points were collected using a Juno 7x global positioning system (GPS) device with submeter accuracy. The GPS datapoints were differentially corrected on the same day using Trimble GPS Pathfinder Office software. To obtain a near-equal number of sample points for each class, we used a pan-sharpened, very-high-spatial-resolution WorldView-2 image (50 cm GSD, taken on July 2013) and expert knowledge to create more sample points. A total number of 798 samples were prepared and divided into 540 training samples (90 samples per class) and 258 validation samples (43 samples per class). To keep the training samples comparable to the GEOBIA framework, a buffer of 3 pixels was applied to all training samples. The training samples were imported as a training-and-test-area (TTA) mask into an object-based software environment. Figure 3 shows the sample distributions.

2.5. Spectral Library

To assess the quality of the training samples, we built the spectral libraries for each tree species. The general assumption is that each element on the Earth’s surface has a unique spectral signature which can be used to identify that particular element [43]. However, in real-world measurements, this task has proven to be especially difficult. The spectral variability can be influenced by many factors, such as viewing angle, atmospheric effects, water contents, etc. In the case of plants, the spectral variability is influenced by the plant’s age, health, and phenology, to mention only a few factors [44]; thus, within a particular species, the spectral signature variation might not be unique (Figure 4). For this reason, we used the average of the spectral values derived from training polygons on that particular class to build the spectral signature (Figure 4).
Figure 5a shows the spectral reflectance of endmembers collected for six tree species using the training samples and APEX hyperspectral imagery. In general, the spectral library for each tree species class shows a normal healthy vegetation reflectance with a lower reflectance for coniferous tree species (Picea abies) and a higher reflectance for deciduous tree species (Alnus incana, Fraxinus excelsior, Populus x (hybrid), Quercus robur, and Salix alba). According to the spectral library of six tree species, one can consider four regions in the EM spectrum: the VIS (413–700 nm), NIR (700–1350 nm), near-SWIR (1457–1796 nm), and far-SWIR (1974–2451 nm) portions of the spectrum (Figure 5b–e). As it is shown in Figure 6b, Salix alba (maroon color) had the highest reflectance among all tree species. The second highest reflectance in the VIS portion of the spectrum belonged to Alnus incana (light green color), followed by Populus x (hybrid; cyan color). The lowest reflectance, as expected, belonged to Picea abies (dark green color). In the near-infrared portion (700–1350 nm), Fraxinus excelsior had the highest reflectance, whereas the overlapping reflectances of Salix alba and Alnus incana on top of each other made it difficult to distinguish them. Populus x (hybrid), Quercus robur, and Picea abies appeared to be distinguishable using the near-infrared portion. Finally, the third portion of the spectrum (near-SWIR; 457–1796 nm) could be used for distinguishing the deciduous and coniferous classes; however, deciduous class separation seems to be challenging due to the overlap of Alnus incana, Fraxinus excelsior, and Salix alba, as well as the overlap between Populus x (hybrid) and and Quercus robur. The fourth portion of the spectrum (far-SWIR; 1974–2451 nm) could be used for the separation of deciduous and coniferous plants.

2.6. APEX Hyperspectral Image Preprocessing

The preprocessing of the APEX hyperspectral imagery comprised two main steps: first, removing noisy bands from the hyperspectral hypercube, and second, creating a non-forest mask.
Noisy bands are characterized by a low signal-to-noise ratio (SNR), meaning that less useful information is present in such bands [45]. The SNR found in the hyperspectral imagery varies by image, and the indication of high or low SNR is highly application-dependent. In this study, noisy bands were selected using their band statistics. Considering a minimum value of 0 and a maximum value of 1 for each band, a band was labelled noisy when its mean value was more than 0.9 and the standard deviation was less than 0.1. Visual inspection was also performed on the potentially noisy bands. A total of 20 noisy bands, ranging from 1359 nm to 1406 nm and from 1813 nm to 1921 nm, were selected and omitted from further analysis. Figure 6 shows an example of normal bands and noisy bands with higher and lower SNR, respectively.
The second step was to mask non-forested areas from the image. Extraction of non-forested areas is especially useful for applying blind signal separation (BSS) such as PCA, MNF, and ICA transformations [46]. By excluding non-forested areas (for example, urban, roads, industrial areas, waterbodies, agriculture areas), the spectral variations of non-forested areas will not influence the signal separation, as the transformation will be related to within-forest spectral heterogeneity. The non-forest vector layer was digitized manually, and the APEX hyperspectral imagery was clipped accordingly in the Arc-GIS software, leading to the spatial extent as shown in Figure 1.

2.7. Data Processing

The data processing was done using ENVI software, version 5.0 (Exelis Visual Information Solution, Munich, Germany). Although no pre-existing knowledge is required for performing the BSS techniques, applying the ICA transformation to 268 spectral bands, each containing 5 × 106 pixels, was a very time-consuming task. Therefore, the transformation was applied to every second row and column of the image, meaning that the image was resized to one-half in terms of rows and columns. The process of resizing was done internally and did not affect the output results. The MNF transformation was the only process among the three that required estimation of noise parameters for the calculation of noise statistics. The best way of introducing sample noise to the process is by selecting a homogeneous dark area in the image. In this study, the black lines in the APEX hyperspectral imagery were used to calculate a noise covariance matrix. The resulting components from each of the dimensionality reduction techniques were examined by the eigenvalues’ measures. Eigenvalues are an indicator for the separation of noise-dominated components (meaning the components with near-unity eigenvalues) from information-dominant components (eigenvalues greater than 1) and visual inspection for band selection. In this research, the stack of DR-transferred components was referred to as a data cube, and the original APEX hyperspectral imagery was referred to as a hypercube.

2.8. Image Segmentation

During the last decades, it has been shown that by increasing a spatial resolution of remote sensing data, per-pixel analysis might not be adequate to extract features of interest [22,23,27]. In contrast to pixel-based analysis, in the GEOBIA framework, segments are considered as the basis of analysis. The idea of segmentation is to spatially decompose complexity [47]. The resulting segments (according to some homogeneity criteria) are considered to maximize spectral homogeneity between segments while minimizing spectral variability within a segment [48,49]. In the context of the GEOBIA, objects are increasingly over- or under-segmented; however, Liu and Xia 2010 [50] argued that segmentation accuracies decrease with increasing segmentation scales, and the negative impacts of under-segmentation errors become significantly large at large scales. Moreover, in the case of over-segmentation, it is possible to merge primary segmentation results to build complex objects. Belgiu and Drǎguţ 2014 [51] argued that a higher classification accuracy can still be achieved as long as under-segmentation remains at an acceptable level. An optimal segment has minimum internal variations and, the same time, maximum external difference from neighboring segments. These optimal segments (also referred as “candidate objects” [52]) strongly depend on segmentation methods. Moreover, the segmentation results are sensitive to many factors, such as sensor resolution, image complexity, and number of bands [53].
The super-pixel segmentation algorithm gained attention due to its simplicity regarding parameterization and its good performance [54]. It is a graph-based or gradient-ascent technique which creates super-pixels (segments) by minimizing a cost function defined over a graph. Super-pixels have a scale between the pixel level and the object level. A simple linear iterative cluster (SLIC) super-pixel algorithm is an adaptation of K-means clustering for super-pixel generation but is faster and more memory efficient [55]. The three new DR data cubes were segmented into homogenous objects using super-pixel segmentation implemented in eCognition software, version 9.3. The super-pixel segmentation was also performed on the APEX hyperspectral imagery. The number of iterations and minimum element size were kept at default in eCognition software. The region size parameter was set to 5 after empirical optimization.

2.9. Classification

The machine learning algorithms such as RF [56], convolutional neural network (CNN), and deep learning have shown promising results in hyperspectral image classification [57,58,59,60]. The RF classifier in particular has gained much attention, especially for the classification of ecology- and biodiversity-related features [61], as well as for handling more complex data such as hyperspectral imagery [62,63,64,65]. A detailed review of RF can be found in [62] and [66]. The RF classifier is an ensemble classifier that produces multiple decision trees using a randomly selected subset of training data and variables. In this study, the RF classifier implemented in eCognition software was used. There are two main parameters to be adjusted for applying the RF algorithm: namely, (a) the number of trees, which, as the name indicates, will determine the number of trees created by randomly selecting samples out of the training samples (Ntree parameter), and (b) the number of variables used for tree node splitting (Mtry parameter). Previous studies have shown that the classification accuracy is more sensitive to the Mtry parameter and hardly affected by the Ntree parameter [46]. Most recommendations suggest setting the Ntree parameter to 500 because the errors are stabilized before this number of classification trees is achieved. It is recommended to set the Mtry parameter to the square root of the number of input variables due to computational concerns. For all spectral DR data cubes, the Ntree parameter was set to 500, and the Mtry parameter was adjusted to the number of input bands. As for the classification of the original APEX hyperspectral image, once all spectral bands (268 bands) were used as the input to the Mtry parameter, and once the Mtry parameter was set to the square root of all bands (√268 = 16.37) and rounded to 17.

2.10. Classification Accuracy Assessment

The accuracies of classification were evaluated according to the following parameters: the confusion matrix, the user’s accuracy, the producer’s accuracy [67,68], and the kappa coefficient [69]. The same validation samples (258 samples, including 43 samples per class) were used for assessing the accuracy of the tree species classifications. We used McNemar’s test [70] for testing the statistical significance of classifications. McNemar’s test is based upon a chi-square (χ2) distribution with one degree of freedom. McNemar’s test is recommended when the same validation samples were used for different classification results. The reason for this is that in such cases, the assumption of sample independence is not fulfilled [71].

3. Results

3.1. Data Processing Results

The APEX hyperspectral imagery was used as the input for performing the PCA, MNF, and ICA transformations. Band selection was done according to eigenvalue measures and visual inspection where the trees were recognizable in the transferred components.
New data cubes were created separately for each dimension reduction technique. The super-pixel segmentation was applied separately to each of the data cubes. Table 1 shows the number of selected bands and the resulting segment bands, a spatial subset of false color composition for each dimensionality reduction technique, and super-pixel segmentation results.

3.2. Spectral Library of the Training Samples Using PCA, MNF, and ICA Inputs

We built the spectral libraries for six tree species to inspect the spectral separability of the training samples. The three DR data cubes were used, and their results were examined (Figure 7). The spectral separability was most pronounced in the ICA transformation, followed by the MNF and the PCA transformations. The spectra plot of the ICA transformation was particularly noteworthy; for example, considering the spectra absorption, Alnus incana (light green) could be distinguished using band number 3, Picea abies (dark green) could be distinguished using band number 4, Populus x (hybrid; cyan color) could be distinguished using band number 6, and Salix alba (maroon color) could be distinguished using band number 7 (Figure 7).

3.3. Classification Results

Figure 8 shows tree species classification results using RF on three DR data cubes and the original APEX hyperspectral image with two different Mtry parameters (268 and 17). Visual inspection was carried out on five classification results to find noticeable errors. For better illustration of the classification results, an example of a tree class was selected, and the classification results are shown in Figure 9.

3.4. Accuracy Assessment

The overall accuracy assessments and kappa coefficient results are shown in Table 2. The overall classification results for the dimensionality reduction techniques achieved good results: the ICA transformation achieved the best classification results (97% overall accuracy, 0.972 kappa coefficient), followed by the MNF transformation (94% overall accuracy, 0.939 kappa coefficient) and the PCA transformation (92% overall accuracy, 0.911 kappa coefficient). The classification of the APEX hyperspectral hypercube (with 268 and 17 bands) achieved the poorest results. A comparison of the classification results of the APEX hyperspectral imagery using all bands versus classification using only the square root of bands (17 bands) showed that using fewer bands did not influence the results significantly. In both cases, values of 80% were achieved for overall accuracy with nearly the same kappa coefficient of 0.76.

3.5. Comparison of Classification Results According to McNemar’s Test

We used the total number of 258 samples (43 samples for each class) to assess the accuracy of classification. The differences between the classification results were assessed using McNemar’s chi-square test (Table 3). The classification results of the ICA transformation and the MNF transformation yielded a comparable result, while the classification outputs of all other transformations were statistically not significant.
The performance of classification results for each class category was assessed by the producer’s and user’s accuracy (Figure 10). According to the producer’s accuracy, Salix alba (more than 95%), and Picea abies (more than 97%) showed the best performance of all the classification results. The second-best performance belonged to Fraxinus excelsior, with a producer’s accuracy of more than 84%, and Alnus incana with a producer’s accuracy of more than 86%. The performance of the two other tree species—Populus x (hybrid) and Quercus robur—showed the poorest accuracy with 50% and 58%, respectively. According to the user’s accuracy, the performance of Salix alba (more than 97%), Populus x (hybrid) (more than 88%), and Picea abies (more than 91%) reached good results. The other three species—Alnus incana (75%), Quercus robur (73%), and Fraxinus excelsior (64%)—showed the poorest performance.
We derived the following deductions according to the performance of the tree species classification using each method:
  • Salix alba achieved a very good performance in all the classification results (producer’s accuracy of 98% to 100%).
  • Populus x (hybrid): The best performance belonged to the ICA transformation. The poorest performance belonged to the results achieved from the APEX original image as an input (producer’s accuracy of 50%). The results achieved from the MNF and the PCA transformations were nearly the same (producer’s accuracy of nearly 95%).
  • Picea abies also achieved a very good performance in all the classification results (producer’s accuracy of 98% to 100%).
  • Alnus incana achieved a good classification result using DR data cubes as an input (producer’s accuracy of 65% to 100%). The poorest performance belonged to the original APEX hyperspectral image as an input (producer’s accuracy 86%).
  • Fraxinus excelsior: The best performance of the classification belonged to the MNF, and ICA transformations and the original APEX hyperspectral imagery (producer’s accuracies of 95%, 93%, and 91%, respectively). The poorest performance belonged to the PCA transformation with a producer’s accuracy of 84%.
  • Quercus robur had the poorest performance in comparison to the classification results of all other tree species. The best performance belonged to the ICA transformation (producer’s accuracy of 93%), and the poorest performance belonged to the original APEX as an input (producer’s accuracy of about 60%).
The confusion matrices are presented in Appendix A.

4. Discussion

4.1. Spectral Dimensionality Reduction

Due to the detailed high spatial and spectral resolution of hyperspectral imagery, it is well suited for use in tree species classification [10]. However, to cope with high data dimensionality (Hughes phenomenon), it is recommended to reduce the spectral dimensionality to reduce the associated problems. We used three BSS dimensionality reduction techniques (namely the ICA, PCA, and MNF transformations) to reduce the spectral dimensionality of the APEX hyperspectral imagery. As shown in Table 2, the PCA transformation was able to reduce the spectral dimensionality into 20 spectral components, the MNF transformation into 35 spectral components, and the ICA transformation into 27 spectral components. From a processing perspective, the PCA transformation required the fewest possible parametrizations. The ICA transformation needed parametrization; however, in this study, the default settings were used. In terms of the processing time, the ICA transformation was very time consuming, as it took several hours to run (using 36 GB RAM and a 64-bit Windows 7 Professional operating system).

4.2. Segmentation and Classification

In this study, we applied super-pixel segmentation to the original APEX hyperspectral image and to each of the RD data cubes to reduce the spatial complexity of the APEX hyperspectral imagery from more than 5 × 106 pixels to (approximately) 2 × 105 segments for each data cube (Table 1). The resulting segments were used as building blocks for the tree species classification. The classification results using DR data cubes performed better in comparison to the original APEX hyperspectral imagery. These results are in line with those of other studies which suggested reducing the data dimensionality before classification procedures [36,72]. In terms of the number of variables used as inputs to the RF classifier, it is recommended to use the square root of bands as an input to RF classification procedures. In this study, RF classification was assessed on the original APEX spectral bands with Mtry = 268, and the results were compared to Mtry = 17 (≈ square root of 268). The comparison of classification results did not show subtle differences (Table 2 and Figure 10 and Figure 11), and, according to McNemar’s test, the difference was not statistically significant (Table 3). The comparison among other classification results revealed that the best classification results were achieved by using the ICA-transformed components as the input to the RF classification procedures. The classification results between the PCA- and MNF-transformed components (according to the producer’s and user’s accuracy) did not show a pronounced difference. These results were confirmed by MacNemar’s test (Table 3).
The confusion matrices (Table 2) clearly showed that the ICA transformation produced the best results for classifying all six tree species (Salix alba, Alnus incana, Fraxinus excelsior, Populus x (hybrid), Quercus robur, and Picea abies). Moreover, according to the spectral signature (Figure 7a) and expert knowledge, the ICA transformation seemed to recognize and separate four tree species classes, namely, Picea abies, Alnus incana, Populus x (hybrid), and Salix alba (Figure 11). This type of information can be used for knowledge-based classification [73].

4.3. Tree Species Classification

According to the producer’s and user’s accuracy, Salix alba and Picea abies had the best performance among the classes. The other four tree species (Populus x (hybrid), Alnus incana, Fraxinus excelsior, and Quercus robur) performed differently in terms of classification accuracy. According to the confusion matrices (Appendix A, Table A1, Table A2, Table A3, Table A4 and Table A5), the largest misclassification happened between Populus x (hybrid) and Fraxinus excelsior, and Quercus robur. These misclassifications can be due to many reasons, some of which might be related to the reference data collections, or the particular conditions of the tree class under investigation, such as shadow, health, age, and phenology conditions, or the misclassification happened due to the presence of mixed pixels.

5. Conclusions

In this study, we assessed spectral complexity reduction by performing three blind signal separation (BSS) spectral dimensionality reduction techniques for tree species classification using airborne prism experiment (APEX) hyperspectral imagery. According to the confusion matrices, the independent component analysis (ICA) transformation achieved higher accuracy in comparison to principle component analysis (PCA) and minimum noise fraction (MNF) transformations. Moreover, the ICA transformation was able to derive independent components which can be viewed as a set of mutually exclusive classes (Figure 11). The ICA transformation might also be more appropriate for the unsupervised classification of hyperspectral imagery because it does not assume normality of data. Therefore, it engages higher-order statistics [74].
In terms of spatial complexity reduction, we used super-pixel segmentation due to its high visual and computational performance. According to Blaschke and Piraliliou, 2018 [75], there is no perfect solution to segmentation; instead, one can think of a more flexible approach to building image objects on demand based on image primitives (segments). Although scale is a key factor in any object-based analysis (for object detection and extraction), we did not consider it in this research specifically. Therefore, our future work will focus on how to address (or select) the optimal scale(s) in the framework of geographic object-based image analysis (GEOBIA) for improving high-spatial-resolution hyperspectral imagery.

Author Contributions

Z.D. was responsible for the conceptualization and methodological development, overall data analysis, and writing of the manuscript. S.L. provided remote sensing data, as well reviewing the manuscript and providing scientific supervision. The field data survey was done by both authors.

Funding

The research leading to these results used data acquired with financial support from the European Community‘s Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 263479. (MS.MONINA). The research was partially funded by the Austrian Science Fund (FWF) through the Doctoral College GIScience (DK W1237-N23).

Acknowledgments

The Authors are grateful for the comments from two reviewers, who greatly improved the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The confusion matrix was used to assess the performance of each class using different inputs. We used 43 sample points for each class to assess its accuracy in terms of the producer’s and user’s accuracy (Table A1, Table A2, Table A3, Table A4 and Table A5).
Table
Table A1. The accuracy assessment using the APEX hyperspectral imagery with all the 268 spectral bands as an input to the RF algorithm.
Table A1. The accuracy assessment using the APEX hyperspectral imagery with all the 268 spectral bands as an input to the RF algorithm.
Reference
Salix albaPopulus x (hybrid)Picea abiesAlnus incanaFraxinus excelsiorQuercus roburSumProducer’s accuracy
ClassifiedSalix alba41100104395%
Populus x (hybrid)022 41434350%
Picea abies00420104398%
Alnus incana01037054386%
Fraxinus excelsior00033914391%
Quercus robur11266274363%
Sum422544506136258
User’s accuracy98%88%95%74%64%75%
Table
Table A2. The accuracy assessment using the APEX hyperspectral imagery with the square root of 268 (16.37, which was rounded to 17) as an input to the RF algorithm.
Table A2. The accuracy assessment using the APEX hyperspectral imagery with the square root of 268 (16.37, which was rounded to 17) as an input to the RF algorithm.
Reference
Salix albaPopulus x (hybrid)Picea abiesAlnus incanaFraxinus excelsiorQuercus roburSumProducer’s accuracy
ClassifiedSalix alba41110004395%
Populus x (hybrid)022041434351%
Picea abies004201 4398%
Alnus incana01037004386%
Fraxinus excelsior00024014393%
Quercus robur11367254358%
Sum422546496229258
User’s accuracy98%88%91%76%65%74%
Table
Table A3. The accuracy assessment using the PCA data cube (with 20 components) as an input to the RF algorithm.
Table A3. The accuracy assessment using the PCA data cube (with 20 components) as an input to the RF algorithm.
Reference
Salix albaPopulus x (hybrid)Picea abiesAlnus incanaFraxinus excelsiorQuercus roburSumProducer’s accuracy
ClassifiedSalix alba430000043100%
Populus x (hybrid)040 1204393%
Picea abies0042 014398%
Alnus incana00041024395%
Fraxinus excelsior00003674384%
Quercus robur2 103374386%
Sum454043424247258
User’s accuracy96%100%98%98%86%79%
Table
Table A4. The accuracy assessment using the MNF data cube (with 35 components) as an input to the RF algorithm.
Table A4. The accuracy assessment using the MNF data cube (with 35 components) as an input to the RF algorithm.
Reference
Salix albaPopulus x (hybrid)Picea abiesAlnus incanaFraxinus excelsiorQuercus roburSumProducer’s accuracy
ClassifiedSalix alba430000043100%
Populus x (hybrid)14100104395%
Picea abies004300043100%
Alnus incana00041204395%
Fraxinus excelsior00004124395%
Quercus robur20014364384%
Sum464143424838258
User’s accuracy93%100%100%98%85%95%
Table
Table A5. The accuracy assessment using the ICA data cube (with 27 components) as an input to the RF algorithm.
Table A5. The accuracy assessment using the ICA data cube (with 27 components) as an input to the RF algorithm.
Reference
Salix albaPopulus x (hybrid)Picea abiesAlnus incanaFraxinus excelsiorQuercus roburSumProducer’s accuracy
ClassifiedSalix alba430000043100%
Populus x (hybrid)043000043100%
Picea abies004300043100%
Alnus incana000430043100%
Fraxinus excelsior00004034393%
Quercus robur00003404393%
Sum434343434343258
User’s accuracy100%100%100%100%93%93%

References

  1. Wetzel, F.T.; Hannu, S.; Eugenie, R.; Corinne, S.M.; Patricia, M.; Larissa, S.; Éamonn, Ó.T.; Francisco, A.G.C.; Anke, H.; Katrin, V. The roles and contributions of Biodiversity Observation Networks (BONs) in better tracking progress to 2020 biodiversity targets: A European case study. Biodiversity 2015, 16, 137–149. [Google Scholar] [CrossRef]
  2. Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, L.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
  3. Martin, M.E.; Newman, S.D.; Aber, J.D.; Congalton, R.G. Determining forest species composition using high spectral resolution remote sensing data. Remote Sen. Environ. 1998, 65, 249–254. [Google Scholar] [CrossRef]
  4. Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
  5. Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
  6. Zhang, J.; Rivard, B.; Sánchez-Azofeifa, A.; Castro-Esau, K. Intra-and inter-class spectral variability of tropical tree species at La Selva, Costa Rica: Implications for species identification using HYDICE imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
  7. Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree species classification in the Southern Alps based on the fusion of very high geometrical resolution multispectral/hyperspectral images and LiDAR data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
  8. Dalponte, M.; Orka, H.O.; Gobakken, T.; Gianelle, D.; Næsset, N. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
  9. Heinzel, J.; Koch, B. Investigating multiple data sources for tree species classification in temperate forest and use for single tree delineation. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 101–110. [Google Scholar] [CrossRef]
  10. Liu, L.; Coops, N.C.; Aven, N.W.; Pang, Y. Mapping urban tree species using integrated airborne hyperspectral and LiDAR remote sensing data. Remote Sens. Environ. 2017, 200, 170–182. [Google Scholar] [CrossRef]
  11. Becker, B.; Lusch, D.P.; Qi, J. A classification-based segmentation of the optimal spectral and spatial resolutions for Great Lakes coastal wetland imagery. Remote Sens. Environ. 2006, 108, 111–120. [Google Scholar] [CrossRef]
  12. Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Hughes, R.F. Invasive species detection in Hawaiian rainforests using airborne imaging spectroscopy and LiDAR. Remote Sens. Environ. 2008, 112, 1942–1955. [Google Scholar] [CrossRef]
  13. Oldeland, J.; Dorigo, W.; Wesuls, D.; Jürgens, N. Mapping bush encroaching species by seasonal differences in hyperspectral imagery. Remote Sens. 2010, 2, 1416–1438. [Google Scholar] [CrossRef]
  14. Harrison, D.; Rivard, B.; Sanchez-Azofeifa, A. Classification of tree species based on longwave hyperspectral data from leaves, a case study for a tropical dry forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 93–105. [Google Scholar] [CrossRef]
  15. Castro, K.L.; Sanchez-Azofeifa, G.A. Changes in spectral properties, chlorophyll content and internal mesophyll structure of senescing Populus balsamifera and Populus tremuloides leaves. Sensors 2008, 8, 51–69. [Google Scholar] [CrossRef] [PubMed]
  16. Sánchez-Azofeifa, G.A.; Castro, K.; Wright, S.J.; Gamon, J.; Kalacska, M.; Rivard, B.; Schnitzer, S.A.; Feng, J.L. Differences in leaf traits, leaf internal structure, and spectral reflectance between two communities of lianas and trees: Implications for remote sensing in tropical environments. Remote Sens. Environ. 2009, 113, 2076–2088. [Google Scholar] [CrossRef] [Green Version]
  17. Hughes, G. On the mean accuracy of statistical pattern recognizers. Trans. Inform. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
  18. Richter, R.; Reu, B.; Wirth, C.; Doktor, D.; Vohland, M. The use of airborne hyperspectral data for tree species classification in a species-rich Central European forest area. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 464–474. [Google Scholar] [CrossRef]
  19. Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, J.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, 110–122. [Google Scholar] [CrossRef]
  20. Hamada, Y.; Stow, D.A.; Coulter, L.L.; Jafolla, J.C.; Hendricks, L.W. Detecting Tamarisk species (Tamarix spp.) in riparian habitats of Southern California using high spatial resolution hyperspectral imagery. Remote Sens. Environ. 2007, 109, 237–248. [Google Scholar] [CrossRef]
  21. Baatz, M.; Schäpe, A. Multiresolution segmentation-an optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung; Strobl, J., Blaswchke, T., Griesebner, G., Eds.; Wischmann-Verlag: Heidelberg, Germany, 2000; Volume 12, pp. 12–23. [Google Scholar]
  22. Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
  23. Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van der Meer, F.; Van der Werff, H.; Van Coillie, F.; et al. Geographic object-based image analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
  24. Lang, S.; Corbane, C.; Pernkopf, L. Earth observation for habitat and biodiversity monitoring. In Creating the GIScociety, GI_Forum 2013, Salzburg, Austria, 2–5 July 2013; Wichmann-Verlag: Berlin, Germany, 2013; pp. 478–486. ISBN 978-3-87907-532-4. [Google Scholar] [CrossRef]
  25. Lang, S. Object-based image analysis for remote sensing applications: Modeling reality—Dealing with complexity. In Object Based Image Analysis-Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G., Eds.; Springer: Berlin, Germany, 2008; pp. 3–28. ISBN 978-3-540-77057-2. [Google Scholar]
  26. Kamal, M.; Stuart, P. Hyperspectral data for mangrove species mapping: A comparison of pixel-based and object-based approach. Remote Sens. 2011, 3, 2222–2242. [Google Scholar] [CrossRef]
  27. Chen, G.; Weng, Q.; Hay, G.J.; He, Y. Geographic Object-based Image Analysis (GEOBIA): Emerging trends and future opportunities. GISci. Remote Sens. 2018, 55, 159–182. [Google Scholar] [CrossRef]
  28. Plaza, A.; Martinez, P.; Plaza, J.; Perez, R. Dimensionality reduction and classification of hyperspectral image data using sequences of extended morphological transformations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 466–479. [Google Scholar] [CrossRef] [Green Version]
  29. Thenkabail, A.; Lyon, P.S.; Huete, J.G.; Bajwa, S.G.; Kulkarni, S.S. Hyperspectral Data Mining. In Hyperspectral Remote Sensing of Vegetation, 1st ed.; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2011; Chapter 4; pp. 93–120. [Google Scholar]
  30. Bajwa, S.G.; Bajcsy, P.; Groves, P.; Tian, L.F. Hyperspectral image data mining for band selection in agricultural applications. Trans. ASAE 2004, 47, 895–907. [Google Scholar] [CrossRef]
  31. Thenkabail, P.S.; Lyon, J.G.; Huete, A. Advances in Hyperspectral Remote Sensing of Vegetation and Agricultural Croplands. In Hyperspectral Remote Sensing of Vegetation, 1st ed.; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2011; Chapter 1; pp. 3–35. [Google Scholar]
  32. Jolliffe, I. Principal component analysis. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1094–1096. [Google Scholar] [CrossRef]
  33. Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef] [Green Version]
  34. Comon, P. Independent component analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
  35. Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
  36. Underwood, E.; Ustin, S.; DiPietro, D. Mapping nonnative plants using hyperspectral imagery. Remote Sens. Environ. 2003, 86, 150–161. [Google Scholar] [CrossRef]
  37. Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
  38. Rodarmel, C.; Shan, J. Principal component analysis for hyperspectral image classification. Surv. Land Inf. Sci. 2002, 62, 115–122. [Google Scholar]
  39. Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Strasser, T.; Lang, S. Object-based class modelling for multi-scale riparian forest habitat mapping. Int. J. Appl. Earth Obs. Geoinf. 2014, 37, 29–37. [Google Scholar] [CrossRef]
  41. Biesemans, J.; Sterckx, S.; Knaeps, E.; Vreys, K.; Adriaensen, S.; Hooyberghs, J.; Meuleman, K.; Kempeneers, P.; Deronde, B.; Everaerts, J. Image processing workflows for airborne remote sensing. Paper Presented at the 5th EARSeL Workshop on Imaging Spectroscopy, Bruges, Belgium, 23–25 April 2007. [Google Scholar]
  42. Haan, J.F.; Kokke, J.M.M. Remote Sensing Algorithm Development: Toolkit I: Operationalization of Atmospheric Correction Methods for Tidal and Inland Waters; Remote Sensing Board (BCRS): Delft, The Netherlands, 1996; ISBN 9054112042. [Google Scholar]
  43. Jensen, R.J. Introductory Digital Image Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
  44. Cochrane, M.A. Using vegetation reflectance variability for species level classification of hyperspectral data. Int. J. Remote Sens. 2000, 21, 2075–2087. [Google Scholar] [CrossRef]
  45. Smith, G.; Curran, P. The signal-to-noise ratio (SNR) required for the estimation of foliar biochemical concentrations. Int. J. Remote Sens. 1996, 17, 1031–1058. [Google Scholar] [CrossRef]
  46. Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
  47. Zhang, Y.J. A survey on evaluation methods for image segmentation. Pattern Recognit. 1996, 29, 1335–1346. [Google Scholar] [CrossRef]
  48. Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
  49. Haralick, R.M.; Linda, G.; Shapiro, L.G. Image segmentation techniques. Presented at the 1985 Technical Symposium East, Arlington, VA, USA, 8–12 April 1985. [Google Scholar]
  50. Liu, D.; Xia, F. Assessing object-based classification: Advantages and limitations. Remote Sens. Lett. 2010, 1, 187–194. [Google Scholar] [CrossRef]
  51. Belgiu, M.; Drǎguţ, D.; Strobl, J. Quantitative evaluation of variations in rule-based classifications of land cover in urban neighbourhoods using WorldView-2 imagery. ISPRS J. Photogramm. Remote Sens. 2014, 87, 205–215. [Google Scholar] [CrossRef] [PubMed]
  52. Burnett, C.; Blaschke, T. A multi-scale segmentation/object relationship modelling methodology for landscape analysis. Ecol. Model. 2003, 168, 233–249. [Google Scholar] [CrossRef]
  53. Hay, G.J.; Castilla, G. Geographic object-based image analysis (geobia): A new name for a new discipline. In Object-Based Image Analysis; Blaschke, T., Lang, S., Hay, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 75–89. [Google Scholar]
  54. Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC super-pixels compared to state-of-the-art super-pixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
  55. Csillik, O. Fast segmentation and classification of very high resolution remote sensing data using SLIC super-pixels. Remote Sens. 2017, 9, 243. [Google Scholar] [CrossRef]
  56. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  57. Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
  58. Liu, T.; Abd-Elrahman, A.; Morton, J.; Wilhelm, V.L. Comparing fully convolutional networks, random forest, support vector machine, and patch-based deep convolutional neural networks for object-based wetland mapping using images from small unmanned aircraft system. GISci. Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
  59. Guidici, D.; Clark, M.L. One-Dimensional convolutional neural network land-cover classification of multi-seasonal hyperspectral imagery in the San Francisco Bay Area, California. Remote Sens. 2017, 9, 629. [Google Scholar] [CrossRef]
  60. Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
  61. Cutler, D.R.; Edwards, T.C.; Beard, k. H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
  62. Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
  63. Bosch, A.; Zisserman, A.; Munoz, X. Image classification using random forests and ferns. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janerio, Brazil, 14–21 October 2007. [Google Scholar] [CrossRef]
  64. Chan, J.C.W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
  65. Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS. J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
  66. Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
  67. Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
  68. Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2009; ISBN 978-1-4200-5512-2. [Google Scholar]
  69. Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
  70. Bradley, J.V. Distribution-Free Statistical Tests; Air Force Aerospace Medical Research Lab: Wright-Patterson AFB, OH, USA; Unwin Hyman: London, UK, 1968. [Google Scholar]
  71. Foody, G.M. Thematic map comparison. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
  72. Rivera-Caicedo, J.P.; Verrelst, J.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Hyperspectral dimensionality reduction for biophysical variable statistical retrieval. ISPRS J. Photogramm. Remote Sens. 2017, 132, 88–101. [Google Scholar] [CrossRef]
  73. Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef] [Green Version]
  74. Shah, C.A.; Arora, M.K.; Varshney, P.K. Unsupervised classification of hyperspectral data: An ICA mixture model based approach. Int. J. Remote Sens. 2004, 25, 481–487. [Google Scholar] [CrossRef]
  75. Blaschke, T.; Piralilou, S.T. The near-decomposability paradigm re-interpreted for place-based GIS. Presented at the 1st Workshop on Platial Analysis (PLATIAL’18), Heidelberg, Germany, 20–21 September 2018. [Google Scholar]
Ijgi 07 00488 g001 550
Figure 1. Study area: the Salzachauen floodplain located on the eastern side, Austria. The background image is a very-high-resolution WorldvIew-2 image. The red box shows the coverage of the airborne prism experiment (APEX) hyperspectral imagery, and the blue polygon illustrates the area of interest which was used in this study.
Figure 1. Study area: the Salzachauen floodplain located on the eastern side, Austria. The background image is a very-high-resolution WorldvIew-2 image. The red box shows the coverage of the airborne prism experiment (APEX) hyperspectral imagery, and the blue polygon illustrates the area of interest which was used in this study.
Ijgi 07 00488 g001
Ijgi 07 00488 g002 550
Figure 2. The workflow included (1) and (2) preprocessing of the APEX hyperspectral imagery to remove noisy bands, and to create non-forest mask; (3) applying three different spectral dimensionality reduction techniques, namely, principal component analysis (PCA), minimum noise fraction (MNF), and independent component analysis (ICA); (4) segmentation of the results using super-pixel segmentation; (5) tree species classification using the random forest (RF) algorithm; and (6) validation of the results and assessment of each dimensionality reduction technique.
Figure 2. The workflow included (1) and (2) preprocessing of the APEX hyperspectral imagery to remove noisy bands, and to create non-forest mask; (3) applying three different spectral dimensionality reduction techniques, namely, principal component analysis (PCA), minimum noise fraction (MNF), and independent component analysis (ICA); (4) segmentation of the results using super-pixel segmentation; (5) tree species classification using the random forest (RF) algorithm; and (6) validation of the results and assessment of each dimensionality reduction technique.
Ijgi 07 00488 g002
Ijgi 07 00488 g003 550
Figure 3. Sample distribution (yellow colors). A total number of 798 samples were created and divided into training samples (540) and validation samples (258) for each class.
Figure 3. Sample distribution (yellow colors). A total number of 798 samples were created and divided into training samples (540) and validation samples (258) for each class.
Ijgi 07 00488 g003
Ijgi 07 00488 g004 550
Figure 4. An example of spectral variability (spectral signature) within a particular tree species (Populus x (hybrid)). For this example, the tree’s crowns were extracted using semi-automatic super-pixel segmentation. The spectral signature for each tree crown was created using the average pixel values within each tree crown.
Figure 4. An example of spectral variability (spectral signature) within a particular tree species (Populus x (hybrid)). For this example, the tree’s crowns were extracted using semi-automatic super-pixel segmentation. The spectral signature for each tree crown was created using the average pixel values within each tree crown.
Ijgi 07 00488 g004
Ijgi 07 00488 g005a 550Ijgi 07 00488 g005b 550
Figure 5. Subfigure (a) shows an illustration of spectra for each tree species using training samples and the APEX hyperspectral imagery; subfigures (b–e)) show a detailed look at the spectra in the visible portion of the spectra (VIS; 413–700 nm), near-infrared (NIR; 700–1357 nm), near-short infrared (near-SWIR; 1457–1796 nm), and far-short infrared (far-SWIR; 1974–2451 nm).
Figure 5. Subfigure (a) shows an illustration of spectra for each tree species using training samples and the APEX hyperspectral imagery; subfigures (b–e)) show a detailed look at the spectra in the visible portion of the spectra (VIS; 413–700 nm), near-infrared (NIR; 700–1357 nm), near-short infrared (near-SWIR; 1457–1796 nm), and far-short infrared (far-SWIR; 1974–2451 nm).
Ijgi 07 00488 g005aIjgi 07 00488 g005b
Ijgi 07 00488 g006 550
Figure 6. An illustration of a normal band (left) and a noisy band (right). The noisy bands were selected according to mean and standard deviation, as well as visual inspection.
Figure 6. An illustration of a normal band (left) and a noisy band (right). The noisy bands were selected according to mean and standard deviation, as well as visual inspection.
Ijgi 07 00488 g006
Ijgi 07 00488 g007a 550Ijgi 07 00488 g007b 550
Figure 7. Spectra of training samples for each tree class using spectral dimensionality-reduced images resulting from PCA, MNF, and ICA transformations.
Figure 7. Spectra of training samples for each tree class using spectral dimensionality-reduced images resulting from PCA, MNF, and ICA transformations.
Ijgi 07 00488 g007aIjgi 07 00488 g007b
Ijgi 07 00488 g008a 550Ijgi 07 00488 g008b 550
Figure 8. Overall classification results using the APEX (original bands with Mtry = 268 and Mtry = 17), MNF, ICA, and PCA transformations.
Figure 8. Overall classification results using the APEX (original bands with Mtry = 268 and Mtry = 17), MNF, ICA, and PCA transformations.
Ijgi 07 00488 g008aIjgi 07 00488 g008b
Ijgi 07 00488 g009a 550Ijgi 07 00488 g009b 550
Figure 9. Detailed documentation of tree species classification using different dimensionality-reduced bands. The classification of the original bands from the APEX hyperspectral imagery is also included.
Figure 9. Detailed documentation of tree species classification using different dimensionality-reduced bands. The classification of the original bands from the APEX hyperspectral imagery is also included.
Ijgi 07 00488 g009aIjgi 07 00488 g009b
Ijgi 07 00488 g010a 550Ijgi 07 00488 g010b 550
Figure 10. Performance of each class (producer’s and user’s accuracies).
Figure 10. Performance of each class (producer’s and user’s accuracies).
Ijgi 07 00488 g010aIjgi 07 00488 g010b
Ijgi 07 00488 g011a 550Ijgi 07 00488 g011b 550
Figure 11. The illustration of independent components after the ICA transformation. In each component, the darker pixels (lower pixel values) have a higher probability of that pixel belonging to a particular feature (or class). For instance, according to expert knowledge, the pixels with lower values in each component most likely comprise the Alnus incana distribution in Figure 11a (ICA component number 7), the Picea abies distribution in the Figure 11b (ICA component number 8), the Populus x (hybrid) distribution in Figure 11c (ICA component number 12), and the Salix alba distribution in Figure 11d (ICA component number 13).
Figure 11. The illustration of independent components after the ICA transformation. In each component, the darker pixels (lower pixel values) have a higher probability of that pixel belonging to a particular feature (or class). For instance, according to expert knowledge, the pixels with lower values in each component most likely comprise the Alnus incana distribution in Figure 11a (ICA component number 7), the Picea abies distribution in the Figure 11b (ICA component number 8), the Populus x (hybrid) distribution in Figure 11c (ICA component number 12), and the Salix alba distribution in Figure 11d (ICA component number 13).
Ijgi 07 00488 g011aIjgi 07 00488 g011b
Table
Table 1. The number of reduced bands after applying dimensionality reduction techniques. An example of a false color composite of the first three components for each dimensionality reduction technique are presented.
Table 1. The number of reduced bands after applying dimensionality reduction techniques. An example of a false color composite of the first three components for each dimensionality reduction technique are presented.
BandsNo. of Segments after Super-Pixel Segmentation
APEX image268211,665 Ijgi 07 00488 i001
PCA20207,547 Ijgi 07 00488 i002
MNF35199,762 Ijgi 07 00488 i003
ICA27211,665 Ijgi 07 00488 i004
Table
Table 2. Classification accuracy assessment according to overall accuracy and kappa coefficient.
Table 2. Classification accuracy assessment according to overall accuracy and kappa coefficient.
ICAMNFPCAAPEX (Mtry = 268)APEX (Mtry = 17)
Overall accuracy (%)9794928080
Kappa coefficient0.9720.9390.9110.7670.762
Table
Table 3. Evaluation of classification methods according to McNemar’s test.
Table 3. Evaluation of classification methods according to McNemar’s test.
X2P
ICA–MNF5.1430.0233
MNF–PCA1.250.2636
ICA–PCA1.250.2636
APEX (Mtry = 268)–APEX (Mtry = 17)10

Share and Cite

MDPI and ACS Style

Dabiri, Z.; Lang, S. Comparison of Independent Component Analysis, Principal Component Analysis, and Minimum Noise Fraction Transformation for Tree Species Classification Using APEX Hyperspectral Imagery. ISPRS Int. J. Geo-Inf. 2018, 7, 488. https://doi.org/10.3390/ijgi7120488

AMA Style

Dabiri Z, Lang S. Comparison of Independent Component Analysis, Principal Component Analysis, and Minimum Noise Fraction Transformation for Tree Species Classification Using APEX Hyperspectral Imagery. ISPRS International Journal of Geo-Information. 2018; 7(12):488. https://doi.org/10.3390/ijgi7120488

Chicago/Turabian Style

Dabiri, Zahra, and Stefan Lang. 2018. "Comparison of Independent Component Analysis, Principal Component Analysis, and Minimum Noise Fraction Transformation for Tree Species Classification Using APEX Hyperspectral Imagery" ISPRS International Journal of Geo-Information 7, no. 12: 488. https://doi.org/10.3390/ijgi7120488

APA Style

Dabiri, Z., & Lang, S. (2018). Comparison of Independent Component Analysis, Principal Component Analysis, and Minimum Noise Fraction Transformation for Tree Species Classification Using APEX Hyperspectral Imagery. ISPRS International Journal of Geo-Information, 7(12), 488. https://doi.org/10.3390/ijgi7120488

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop