Analysing the Police Patrol Routing Problem: A Review

Abstract

Police patrol is a complex process. While on patrol, police officers must balance many intersecting responsibilities. Most notably, police must proactively patrol and prevent offenders from committing crimes but must also reactively respond to real-time incidents. Efficient patrol strategies are crucial to manage scarce police resources and minimize emergency response times. The objective of this review paper is to discuss solution methods that can be used to solve the so-called police patrol routing problem (PPRP). The starting point of the review is the existing literature on the dynamic vehicle routing problem (DVRP). A keyword search resulted in 30 articles that focus on the DVRP with a link to police. Although the articles refer to policing, there is no specific focus on the PPRP; hence, there is a knowledge gap. A diversity of approaches is put forward ranging from more convenient solution methods such as a (hybrid) Genetic Algorithm (GA), linear programming and routing policies, to more complex Markov Decision Processes and Online Stochastic Combinatorial Optimization. Given the objectives, characteristics, advantages and limitations, the (hybrid) GA, routing policies and local search seem the most valuable solution methods for solving the PPRP.

1. Introduction

Since the 1990s, law enforcement has been increasingly influenced by the literature on the relationship between crime and place. Technological advances in hardware and software, e.g., the proliferation of computerised police information systems and more affordable Geographic Information Systems (GIS), are at the basis of this increased influence [1]. Furthermore, the use of Global Positioning Systems (GPS) and personal trackers becomes more and more established and data recording systems and communication and information technologies, e.g., computer aided dispatch (CAD), enhanced over the years. Consequently, the range of quantitative analysis methods expanded considerably. On the one hand, data-driven policing, as applied for example in predictive policing applications (e.g., PredPol) will contribute to the improvement of preventive police patrol [1,2,3,4]. On the other hand, in research on routing strategies, similar technological advances led to the availability of real-time information at lower costs, which resulted in a major expansion of the existing solution methods for routing problems [5,6]. Currently, there is a poor understanding of how routine day-to-day patrol intervenes with criminal opportunities. Moreover, police patrol routing strategies which incorporate the responsibilities of police officers on patrol are still missing [7]. To address these deficiencies, this paper examines which algorithms can regulate effective police patrol routing, with a focus on overt or visible crime, i.e., crimes occurring in public places, which can be seen and heard by other people and can draw police attention. Examples of overt crimes are drug-related crimes, car theft, larceny, assaults and burglary. Not only overt crime is of interest to police officers—combating public nuisance is also one of their duties, e.g., vandalism and loitering [8,9,10].

This paper consists of a literature review on the police patrol routing problem (PPRP). The PPRP has the structure of the better-known dynamic vehicle routing problem (DVRP) [11,12], but the knowledge about solving the PPRP is rather limited. Therefore, in this review we focus on papers which consider police patrol routing as a DVRP. A review of the PPRP in particular does not yet exist [11,13]. In this article, we address this and answer the following research question: “What algorithms or strategies exist to solve the police patrol routing problem as a dynamic vehicle routing problem?” This review qualitatively analyses articles on DVRPs with a specific focus on police. The overall objective of this review is to address the gap in the existing knowledge on solution methods for the PPRP. To achieve this overall aim, articles related to this topic will be compiled and their solution methods will be compared and discussed. An evaluation of the classification of the PPRP in terms of its stochastic and dynamic characteristics is also indispensable. This review will result in an overview of solution methods that are convenient to solve the PPRP. The remainder of this paper is organized as follows: In Section 2, the PPRP is defined, in Section 3, we briefly discuss different types of vehicle routing problems, with a focus on the DVRP. Next, in Section 4, we explain the literature search process. In Section 5, we discuss our major findings and demonstrate that certain solution methods are more convenient than others; this depends on the objectives and characteristics of the vehicle routing problem they try to solve. The results and possibilities for future research are discussed in Section 6 and finally in Section 7 we provide some concluding remarks and identify avenues for future research.

2. The Peculiarities of the Police Patrol Routing Problem

Police patrol is one of the most important tasks employed on a daily basis by the police to prevent and reduce crime and respond to emergencies and disasters [14,15]. The visible presence of police officers in a community became one of the key components of routine police patrol since the establishment of the “New Police” in 1829 in England [16,17]. Wise and Cheng [18] describe how police officers create guardianship by reminding individuals of the rule of law and by raising the awareness among potential offenders of the risks associated with committing offences. So, the physical presence or absence of police in time and space influences individual offenders in their decision to commit crime [18,19]. One of the primary goals of proactive patrol is crime prevention. Despite this goal, routine police patrol is, according to the Kansas City Preventive Patrol Experiment in the 1970s, a rather ineffective mode of policing to reduce crime and the public’s fear of crime [10]. As a result, the effectiveness of focused proactive patrol in reducing crime at specific and small geographic areas, so-called hot spots policing, was more extensively studied [20]. This resulted in a wide range of routing strategies solely based on hot spot policing [21,22]. Nevertheless, routine police patrol, which is not geographically constrained to a small number of preidentified high-crime places, is nowadays still central to everyday policing in many police jurisdictions [17,23,24,25]. In light of the general importance of routine police patrol, major technological and methodological advancements during the past five decades and the remaining ambiguity regarding routine police patrol and crime prevention, the efficacy of this policing tactic needs to be revisited and a strategy for routine police patrol has to be developed.

Given the scarcity of police resources, an efficient allocation of the resources to crime deterrent strategies, as well as reactive patrol, is crucial [26]. In the context of the PPRP, a daily shift of police officers can be described as follows: police officers start their shift from a depot. A police vehicle leaves the depot and drives to the allocated patrol beat. While patrolling this area, the patrol unit can be dispatched to an emergency call. Clearly, these interventions are not known in advance. Emergency calls arrive in real-time to a dispatch centre, which subsequently directs the vehicle on site. The police vehicle temporarily has to stop its current task, for example proactive patrol, to respond to the emergency call [27]. Depending on the urgency of the call (crime priority codes), the response time should be minimized. The response time is the period between when an emergency call is recorded and the time the first police vehicle arrives on site [28]. Once the emergency call is finished, the police vehicle resumes its ongoing tasks, e.g., the vehicle returns to its patrol beat and resumes its proactive patrolling task [27]. At the end of the shift, the police vehicle drives back to the depot. In larger precincts one of the complexities entails the optimization of the spatial deployment of the police fleet, which is determined by the available number of police officers and vehicles, as well as the number of patrol beats. An increase in the number of cars or the number of districts does not necessarily imply a decrease in response times. So, the optimal spatial deployment for a precinct should be determined to minimize the response times [29]. Furthermore, the available police capacity has to be optimized in time, in particular from the moment a police vehicle is dispatched to an incident [29,30] and in accordance with the spatiotemporal patterns of crime, which will differ depending on the time of day or the day of the week [31,32]. Another important aspect in developing a patrolling strategy is to determine the optimal police dosage, i.e., the patrol frequency and duration, based on the quantification of the effect of visible police presence on crime in time and space, in order to deter crime [2,4,29]. The police dosage can be measured as the time (e.g., minutes) a police unit is present at a certain place [33]. However, it can also be formulated differently and more in line with (probabilistic) ant algorithms; it is interesting to know how long a street segment will be free from crime after a police vehicle passes it (e.g., the pheromone traces in ant algorithms) [34,35].

The aim of this article is to come up with a solution method that can be used to develop a police patrol routing strategy that meets the following objectives and characteristics. First, since the police are financed with public funds, a cost-efficient deployment of the available resources is an important factor [2,4,24,29]. Second, the effectiveness of routine day-to-day patrol in reducing crime and disorder needs to be monitored, which has not yet been established. This is problematic, since police resources are scarce public goods and should therefore be allocated to crime deterrent strategies that are effective [26,36]. Davies and Bowers [4] state, for example, that effectiveness and efficiency depend on the area-specific presence of police officers and the spatial dispersion of crime, i.e., the crime deterrent effect can be increased when the supply of policing and the demand for it are spatially matched [4,8,23]. Furthermore, this is in line with the societal function of police officers in creating a sense of security and reminding people of the rule of law [23,37]. Third, the emphasis can also be on the most optimal spatiotemporal outcome, which can be achieved by focusing on the allocation of the vehicles in time and space. Optimizing the spatiotemporal allocation implies minimizing waiting times, in other words, minimizing response times to emergency calls [28,29,30]. In general, the choice for a certain desired outcome will entail certain trade-offs. For example, a routing strategy that pursues the most optimal spatial deployment of police vehicles in space will probably not be the most cost-efficient strategy, because covering an area as optimal as possible, i.e., without limitations of the amount of officers or vehicles, entails a high cost. When developing a strategy for police patrol routing, as many of the intersecting responsibilities of police officers as possible have to be balanced, which entails making deliberate choices and accepting trade-offs [18,38]. Briefly, in contrast to the existing police patrol routing strategies, a strategy for routine police patrol aims to balance proactive and reactive police patrol in a realistic way (contra [21,22,39]), this is not predominantly focusing on crime hot spots (contra [40]), is not simplified to one single patrol unit or one small patrol beat (contra [27,41]) and targets motorized vehicle patrol (contra [42]).

3. Starting Point: The Dynamic Vehicle Routing Problem

The Vehicle Routing Problem (VRP) is a generalization of the Traveling Salesman Problem (TSP) and was introduced by Dantzig and Ramser in 1959 [43,44]. The VRP is a widely studied NP-hard combinatorial optimization problem and is commonly encountered in the field of Operations Research and the domain of (city) logistics and transport [45,46]. The VRP determines how to serve a set of geographically dispersed customers, by means of designing routes for a fleet of vehicles, dispatched from a (single) depot. The vehicles return to the same depot once the routes have been completed. The objective of VRPs is to optimize the routes by minimizing the total travelled distance, therefore cutting the costs while respecting all constraints [45,47,48,49,50].

A dynamic vehicle routing problem (DVRP) is the dynamic counterpart of the static VRP. Pillac et al. [11] identify a taxonomy of four categories of VRPs, based on the information evolution (i.e., the available information can change throughout the process (static/dynamic)) and the information quality (i.e., the available information may be uncertain (deterministic/stochastic)) [11]. Consequently, vehicle routing problems can be either static, according to the classical definition of the VRP, or dynamic, based on real-world applications, which evolve in real-time [11,51]. In case of the static VRP, all the relevant information is known a priori, i.e., the customers, the routes, the driving time between the customers and the service times are known in advance. This is in contrast to its dynamic counterpart where not all information relevant for the planning and execution of the routes is known in advance. New information, such as the arrival of new customer requests, is revealed dynamically, after the routing process has already started. Therefore, planned routes have to be reoptimized in an ongoing fashion [47]. In case of a static and deterministic VRP, all information is known with certainty, and stochastic information is absent. In contrast, for a static and stochastic VRP, the route is defined a priori but information on the customers is only revealed afterwards. When the VRP is dynamic and stochastic, information on the demand is only revealed when a demand for service occurs or while a customer is visited. Stochastic knowledge about future request can be generated by using past request information, and, using certain algorithms (i.e., tabu search) vehicles can be actively guided to request-likely areas even before requests arrive [11,52]. Clearly, the PPRP falls within the dynamic/stochastic category.

DVRPs have been studied extensively since the late 1970s. Wilson and Colvin [53] were the first to refer to a dynamic dial-a-ride problem. Three years later, Psaraftis [54] introduced a reoptimization algorithm for the current vehicle route. Since 2000, the literature on DVRPs increased. Technological advances led to the development of DVRPs, which created greater opportunities to reduce costs, improve customer services and reduce environmental impact [11,52]. Over the years, a number of other variants of the VRP have been formulated. Common dynamic variants of the VRP are for instance the Capacitated VRP, the VRP with Pick-up and Delivery (PDP), the VRP with Time Windows (VRPTW), Open VRP (O-VRP), and the Dial-A-Ride-Problem (DARP) [11,55]. Due to the NP-hardness of the problem, the computation time can be high. To limit the computation time, using heuristics and metaheuristics will be more efficient to solve real-time DVRPs, since exact algorithms will give the most optimal solution but the computing time will run out [45,56].

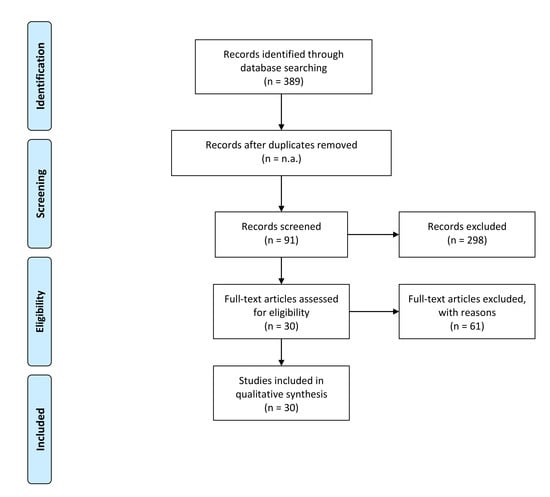
4. In Search for Literature Linking the PPRP to the DVRP

In the literature on police patrol routing, a solution method for routine police patrol, as described above, is still missing. However, the PPRP has a lot in common with stochastic and dynamic VRPs (see Section 5.1). Consequently, analysing the literature on DVRPs and the associated solution methods will contribute to the development of a police patrol routing strategy for routine police patrol. Currently, there already exist a lot of solution methods in the field of Operations Research. So, gathering knowledge about solution methods used to solve comparable routing problems to the PPRP is essential in order to prevent unfolding a redundant new algorithm.

The knowledge gathering is established by a review of the literature on DVRPs. The database searched is the web-based search engine Google Scholar. In a preliminary phase, other databases, including but not limited to Web of Knowledge, ScienceDirect and IEEE Xplore, were also explored. This yielded for each of these databases only a few (irrelevant) or no results. Since this was not the case for Google Scholar, this database is used to conduct this review. The search string used is: ((“dynamic vehicle routing”) AND (police)). Before conducting the actual search, based on this search string, other keyword combinations were also analysed such as (“dynamic vehicle routing problem*” AND (police)). However, “problem*” was not added in the final search because some articles focused for instance on “systems” instead of “problem(s)”, even though the articles consider DVRPs. We also opted to search for “police” and not for “emergency services” in general because routing strategies for the police on the one hand, and ambulances or firefighting on the other hand, differ from each other. Regarding their responsive tasks, the same applies for all three of the emergency services; it is critical to minimize the response times to all types of emergencies [5]. The major difference occurs when the vehicles are idle, i.e., not responding to an emergency call. While police vehicles are assigned to a patrol beat and have to patrol streets [6,7,8], the emergency medical services (EMS) and the fire brigade are redeployed to a base station. The redeployment models can be static (the allocation is fixed and a vehicle is sent back to its home base whenever it becomes idle), or dynamic (at the moment of relocation, the state of the system is taken into account), but they neither have to be visible nor have a preventative task [9,10,11,12]. For the police it is important to quantify the effect of visible police presence on crime in time and space and to determine the optimal dosage of police patrol [4]. Police patrol is composed of proactive or preventive patrolling on the one hand and reactive patrolling on the other hand, both of them having very different characteristics. In day-to-day patrol, proactive patrol routes can be determined based on, for example, the theoretical street network usage (centrality measures) and historical crime data [17]. Consequently, they could be partly determined a priori [4]. Reactive police patrol depends on the incoming calls for emergency, so they cannot be determined in advance. The concept of police patrol is broad, dynamic and complex, but we will try to address this complexity in the course of this paper.

Furthermore, no specifications were made concerning date or place. The PRISMA flow diagram, shown in Figure 1, illustrates the search results [57]. In total, 389 papers were retrieved. Due to the authors’ language proficiency, there might be a language bias because only papers written in English were considered. To further narrow our search, we applied additional selection criteria.

First, each included study needed to describe a strategy or algorithm resolving a DVRP with similar objectives and characteristics as the PPRP, and “police (patrol)” must at least be mentioned in the context of the DVRP. Articles describing another type of DVRP, without referring to police (patrol), are excluded. We also excluded those articles describing the methodology for the dispatching and routing of emergency vehicles (i.e., police vehicles, ambulances, and fire trucks) in a post-disaster environment, for example, following an earthquake or a chemical attack [58,59]. Although, principles of earthquake after-shock models (seismology) and spatial epidemiology are used in predictive policing [60], the articles found in this review only discuss how to react in a post-disaster environment. These situations can be considered as extraordinary, in which most of the characteristics of routine police patrol no longer apply; therefore, they are not included for further analysis. Similar to this, a lot of articles focus on a specific type of DVRP, with specific characteristics not corresponding to the PPRP. To illustrate, in [61] the focus is specifically on the decision making process for the emergency medical services in India. Moreover, police patrol routing takes place at street segment level. Therefore, articles focusing on the deployment of a fleet of vehicles on a higher spatial scale are excluded [62]. Finally, papers that took a different approach to the concept of police patrol, i.e., stating that they had no proactive patrolling task, were excluded as well [63].

Applying these criteria led to a sample of 30 papers (16 journal articles, 6 conference proceedings, 4 book chapters, 1 patent and 3 publicly available reports). Journal articles were mainly drawn from disciplines related to engineering and computer sciences, but there were contributions from management and transport as well. It is remarkable that none of the disciplines were related to criminology, which one might expect given the focus on the police and their patrolling strategies. Our sample of papers is quite diverse in terms of geography (17 different countries can be distinguished). China, the United States of America and Spain were the most represented, with six, five and four papers, respectively. The United Kingdom is only represented with one paper.

The inclusion of an article in the dataset does not necessarily mean that this article elaborates on a solution method specifically designed for the PPRP. On the contrary, none of the 30 articles, with the exception of two [38,64], are examining or solving the DVRP with a focus on police patrol. Instead, “police” is in most of the articles only mentioned or discussed as a (specific) type of DVRP. Considering the purpose of this literature review, this finding is at least remarkable but could be in part explained because of the lack of research within the field of criminology.

The qualitative analysis of the sample is performed manually and is first of all based on the type of article. There are two types of articles, on the one hand, articles describing specific cases and developing new solutions, for example [59], in which a DVRP with soft time windows is solved by a hybrid approach. On the other hand, there are a handful of theoretical articles that provide an overview of extant solution methods for DVRPs. In order to answer the research question, i.e., finding solution methods that are convenient to solve the PPRP, the objectives of the solution methods in the sample have to match the objectives of the PPRP. Subsequently, the solution methods are classified and discussed based on their characteristics. For the case studies, objectives, methods and specific features of importance to the PPRP, as described in Section 2, are comprehensively discussed.

5. Main Findings

5.1. Police Patrol Routing and the Literature on the DVRP

Definitions of police and police patrol differ across the studies. Larsen et al. [47] classify DVRPs into a three echelon framework based on the degree of dynamism and the objective. The degree of dynamism is a measure to express to what extent a routing problem is dynamic. It is measured by the number of dynamic requests relative to the total number of requests (the static and dynamic requests combined) [5,12,65]. The emergency services, including police, are classified as “the most extreme type” of strongly dynamic routing systems. They emphasize that a-priori information is not available. According to this classification, the most important objective for the police is minimizing the response time. The other two echelons are weakly and moderately dynamic systems [47]. As in [47], police are often mentioned as a part of “the emergency services”. Although most of the articles refer to the emergency services as having identical characteristics, caution is required as mentioned above [5,65,66]. Billhardt et al. [67,68] are aware of this specific feature of police patrol and emphasize the patrolling task of the police force without using fixed stations. Watanabe and Takamiya [64] even distinguish between the response time and the carrying frequency, which indicates how often a police vehicle should pass each road segment in one week. In graph theory, most vehicle routing problems are node routing problems, i.e., the nodes of an underlying network or graph represent the customer demand. However, in the case of police patrol, Sbihi and Eglese [69] state that the demands are associated with the edges or arcs of a graph; these are arc routing problems. “The service”, i.e., preventing crime and disorder, is carried out across the length of a road segment. The graph is based on the underlying road network: the street segments are the edges/arcs and the crossings are the nodes [69]. Although the complexity of police patrol is tucked away in the proactive side, it is still underexposed.

There exists a plethora of DVRPs across studies, even in our small sample. Bertsimas and van Ryzin [70,71] elaborate on the Dynamic Traveling Repairman Problem (DTRP). In turn, Gendreau et al. [72] analyse the Maximal Expected Coverage Relocation Problem for emergency services and also Patrascu et al. [66], Shen et al. [73] and Yong and Xinping [74] focus on optimization strategies for the emergency vehicles. In addition, taxi services [67,68], courier services [6,75] and the Min-Max Vehicle Routing Problem (MMVRP) [76] are all types of DVRPs. Despite the fact that (almost) none of these routing problems directly relate to the PPRP, their objectives are broadly consistent with the objectives of the PPRP. In line with the trade-offs between the objectives for the optimization of police patrol, any of the DVRPs can meet conflicting objectives. In a dynamic setting, minimizing the travel distance is not as fundamental as it often is in a static setting. Instead, minimizing the waiting time is a more adequate objective in dynamic environments. In general terms, maximizing the quality of the delivered services is a major objective of DVRPs. Quality here relates to developing effective and efficient routing strategies within a framework of minimizing the routing cost and optimizing throughput, or as [5] (p. 5) puts it, this is “the maximization of the expected number of requests serviced within a given period of time”. Since these objectives are analogous with those described for police patrol routing, it can be assumed that the solution methods developed for these objectives may be important for the PPRP.

5.2. Classifications of Solution Methods for Stochastic DVRPs

5.2.1. Sequential and Parallel Algorithms

Ghiani et al. [5] give a comprehensive overview of solution methods for stochastic and dynamic vehicle routing problems (SDVRP). They emphasize the difference between sequential and parallel algorithms. Sequential algorithms are divided into simple policies, classical insertion procedures and metaheuristics, and they are executed sequentially, without processing other solution methods at the same time. Parallel implementations are needed to limit the compilation time, in order to solve real-time routing and dispatching problems within a short time frame [77]. The computational effort and the overall computation power determine how fast route reoptimization can be done [5,12,72]. Together with the average inter-arrival time of service requests, for example, calls for service, these three factors are important when choosing a parallelization strategy. Parallel computing can be performed on high performance computing platforms or on clusters of computers. According to Ghiani et al. [5], domain decomposition parallelization strategies are convenient strategies for SDVRPs.

In the case of sequential algorithms, Ghiani et al. [5] define the routing policies as “simple rules applied repeatedly in order to dispatch requests to vehicles and build routes.” [5] (p. 5). The policies outlined in [5] try to solve the stochastic and dynamic traveling repairman problem (DTRP). Five policies are discussed: the first-come-first-served policy, the stochastic queue median policy, the nearest neighbour policy, the travelling salesman problem (TSP) policy and the generation policy. In the first-come-first-served policy, the dispatcher serves the demands in the order they arrive. The stochastic queue median policy is a modification of the first-come-first-served policy in which a vehicle is assigned to the stochastic median of a service region whenever not responding to an emergency call. Third, in a nearest neighbour policy, a vehicle serves the nearest neighbouring request after the completion of its current service. Larsen et al. [12], who also consider those three policies, recommend prioritizing the utilization of the nearest neighbour policy for moderate and strongly dynamic systems. Furthermore, the TSP policy solves the requests based on the optimal TSP solution, and since the stochastic queue median policy becomes unstable as the demand rate increases, the fifth routing policy, i.e., the generation policy, is determined [5]. Moreover, Larsen et al. [12] also identify the partitioning policy, which states that the service area is divided into smaller areas, in which the first-come-first-served policy is applied.

By the classical insertion procedures Ghiani et al. [5] indicate heuristics that reoptimize routes when new information, for example, the insertion of new customers, becomes available. Although these heuristics have good empirical performance in several operational conditions and have a fast computation time even on sequential hardware, they do not always provide good solutions. Instead, metaheuristics are used to generate better vehicle routes. Metaheuristics are “iterative procedures aimed at finding near-optimal solutions for large-scale combinatorial optimization problems” [5] (p. 6). Ghiani et al. list the following metaheuristics: simulated and deterministic annealing, genetic algorithms (GA), neural networks, expert systems, ant colony methods, tabu search, adaptive memory techniques and variable neighborhood search [5]. Khouadjia et al. [65], who also give a state of the art of the metaheuristics for the DVRP and its variants, make a distinction between trajectory-based metaheuristics such as tabu search, greedy randomized adaptive search procedure and variable neighbourhood search and population-based metaheuristics such as ant colony optimization, evolutionary algorithms with a focus on GA and particle swarm optimization. They give no further explanation for this division. In turn, Kaiwartya et al. [55] explain “nature inspired” metaheuristics: GA, ant colony optimization and particle swarm optimization. According to them these three metaheuristics are the most commonly used techniques to solve several types of DVRPs.

5.2.2. Path-Based and Time-Based Optimization Methods

The classification of Ghiani et al. [5] acts more or less as an overarching scheme for [12,55,65]. Nevertheless, [13,78] classify the solution methods differently. In their systematic review of route optimization and pre-emption methods for emergency vehicles, the overall objective of [13] is to identify and classify existing techniques which consider the reduction of the travel time of emergency vehicles. They divide the route optimization methods in path-based optimization, time-based optimization, and other optimization methods. In case of the path-based methods, the focus is on Dijkstra’s shortest path algorithm or generalizations of this algorithm, for example, the stochastic shortest path algorithm and the A* algorithm. According to Humagain et al. [13] the time-based optimization methods are even more important for emergency vehicle routing than distance or cost. These include, for example, simulated annealing algorithms, which minimize rescue time and cost, exact pseudo-polynomial algorithms, e-approximation algorithms and Dijkstra’s algorithm for the calculation of the shortest path. Finally, they define some alternative approaches, including but not limited to ant colony optimization and Dijkstra’s algorithm for different traffic conditions. One of the implementation gaps they raise is that commercial emergency vehicle routing software prefers the utilization of simpler heuristics to the route optimization algorithms. Moreover, they emphasize the importance of a limited computing time of the algorithms [13]. Pillac et al. [78] confirm this.

5.2.3. Solution Methods for Deterministic Versus Stochastic DVRPs

In the context of this research and the proposed research question, Pillac et al. [78] make an interesting subdivision between solution methods based on the deterministic or stochastic character of DVRPs. First of all, they propose some approaches that have been used to solve dynamic routing problems, without stochastic information. They then distinguish dynamic programming, linear programming and the following metaheuristics: tabu search, variable neighbourhood search, Large Neighbourhood Search, Multiple Plan Approach, Evolutionary Algorithms (e.g., GA) and ant colony optimization. In contrast, when stochastic information is available in the dynamically revealed input, they identify sampling and pricing strategies. The goal of sampling strategies is “to capture the likeliness of an event and create a routing plan that will be able to accommodate it” [78] (p. 19). Pricing strategies evaluate expected values, while they know the probability of the arrival of a new request in the meantime. First, Pillac et al. [78] describe a Markov Decision Process and Approximate Dynamic Programming, both examples of pricing strategies. Approximate dynamic programming includes predictive algorithms, which can take predictive or preventive actions. This may be of interest for the proactive side of police patrol routing. The Online Stochastic Combinatorial Optimization is a collective term for predictive approaches for the SDVRP such as, for example, Multiple Scenario Approach. In addition to these strategies, Pillac et al. [78] also mention strategies that introduce sampling or pricing to deterministic methods, including but not limited to: Dynamic Sample Scenario Hedge Heuristic (DSHH), local search approaches, tabu search and linear programming. Moreover, for example “relocating strategies” aim to relocate idle vehicles to strategic locations for the purpose of producing adequate response to upcoming events. According to them, this is the keystone of emergency fleet deployment. Other, similar strategies are waiting strategies and request buffering [78].

5.3. Application of Solution Methods

The solution methods are rather diverse.

Table 1. Overview of the different types of problems and their solution methods.

Type	Solution Methods	Articles
Dynamic Vehicle Routing Problem	Routing policies, (hybrid) GA, optimization strategies, heuristic optimization methods, shortest path algorithm, local search	[64,66,70,71,73,76,77,80,81,82,83,84]
Dynamic Vehicle Dispatching Problem	Genetic programming, GA, response strategies, a dynamic assignment strategy, linear programming, reinforcement learning	[6,74,75,79,82,85]
Dynamic fleet management system	Routing policies, a decentralized algorithm	[67,68]
Patrol beat scheduling	A chance-constrained optimization model	[38]
The maximal expected coverage relocation problem	A single integer linear program	[72]
Classification of solution methods on the DVRP	Simple policies, classical insertion procedures, (meta)heuristics, …	[5,12,13,47,55,65,69,78,86]

gives an overview of the methods used. It is important to know that not all the articles examine a DVRP as it is described in Section 2. For example, some rather consider dynamic vehicle dispatching instead of dynamic vehicle routing. Moreover, the impact of traffic on the generation or optimization of (new) routes gets a lot of attention. Patrascu et al. [66] examine how they can obtain the shortest routes for emergency vehicles in an urban context. They emphasize that the shortest path does not necessarily correspond to the fastest path, as a result of traffic congestion. Moreover, they take into account that the occupancy of road segments is variable and might change while a vehicle is already on its route. To solve this routing problem, they propose a GA, because of the ability of this optimization heuristic “[…] to perform rapid searches in large amounts of uncertain or incomplete data, with an inherent structure that allows parallelization” [66] (p. 244). Patrascu et al. [66] tested the algorithm in a simulated environment, which showed great potential to develop an algorithm that can be tested under real world conditions. GAs are applied in several cases, both for dispatching and routing problems [66,74,76,77,79,80].

Other strategies used to solve routing problems are different types of policies: first-come-first-served policies, partitioning policy, traveling salesman policy, the space filling curve policy and the nearest neighbour policy. In the case of light traffic conditions, the first-come-first-served policy is the most optimal. In contrast, in heavy traffic, the traveling salesman policy, space filling curve policy and nearest neighbour policy are the best options (see

Table 2. Advantages and limitations of the most convenient solution methods for the police patrol routing problem (PPRP).

Solution Method	Advantages	Limitations
(Hybrid) Genetic Algorithm	→ Powerful tool applicable to different optimization problems → Performs rapid searches in large amounts of uncertain or incomplete data → Recalculation of the routes during patrol → High solving quality → Good results with a large number of customers → A possibility to run locally → Parallelization is possible → Traffic can be taken into account → Hybridization: cumulative benefits of different metaheuristics	→ Inherent heuristic nature of GA: it requires a sort of hybridization with formal methods, metaheuristics or memetic algorithms to give a comprehensive result → Although limited, the requests on the processing time are quite high
Routing Policies	→ Traffic can be taken into account: → Light traffic: FCFS most optimal → Heavy traffic: TSP, SFC and NN most optimal → Provable performance guarantees → NN most efficient in strongly dynamic systems	→ FCFS is unstable in high traffic situations
Local Search based on Network Voronoi Diagram	→ The initial routes are dynamically optimized while on patrol. → Response time and carrying frequency are taken into account → Aims to compute semi-optimal solutions speedily → Positional balance among patrol vehicles	→ Formulation of the problem is complex → No clear link with SDVRPs
Approximate Dynamic Programming	→ Predictive algorithm (predictive or preventive actions)	→ Curse of dimensionality (useless with too vast state or action spaces)
Multiple Scenario Approach	→ Predictive algorithm

) [70,71]. Subsequently, Haghani et al. [82] evaluate three different response strategies (first-come-first-served policy, nearest-origin assignment and the flexible assignment strategy) with a simulation model. The flexible assignment strategy performs the best in a dynamic context. Bouziyane et al. [77] use a hybrid algorithm that combines GA and variable neighbourhood search to solve a DVRP with soft time windows, and Ren [76] applies a hybrid GA. Gendreau et al. [72] in turn developed a dynamic relocation strategy based on linear programming. Shen et al. [73] developed the Self-Adaptive Interactive Navigation Tool+, called “SAINT+” for emergency service delivery optimization. The objective of this tool is to reduce the delivery time of emergency services, taking traffic congestion into account. Watanabe and Takamiya [64] developed a strategy specifically for police patrol routing. In their optimization method, they use the local search technique based on a network voronoi diagram. This results in a patrol route that satisfies the carrying frequencies of the edges and that balances the presence of police vehicles in time and space [64].

In the case of dispatching problems, a parallel tabu search algorithm is used by Ichoua et al. [6], Benyahia and Potvin [79] use genetic programming (i.e., extending GA to nonlinear structures) and linear programming is combined with reinforcement learning in [85]. In some articles it is less clear what specific algorithms are used to solve routing or dispatching problems [84]. Benyahia and Potvin [75] developed a framework architecture for dynamic vehicle dispatching and categorized the different functions of vehicle dispatching and assigned a technical component to each of them. For example, shortest path algorithms are assigned to “the assignment of new requests”, but exact or approximate methods (e.g., metaheuristics) can be selected for “route planning”. Furthermore, several articles use simulation models, for example DYNASMART, a simulation-assignment model that is used to evaluate dispatching and routing strategies for individual vehicles [83].

5.4. Performance Evaluation of the Solution Methods

In analogy with performance assessments of methods or algorithms used to solve static VRPs, new metrics should be introduced to assess the performance of the proposed solution methods for SDVRPs. On the one hand, a few articles shed light on measures that can be applied to evaluate the performance. Khouadjia et al. [65] discuss three measures: the optimization accuracy, the stability, and the ɛ-reactivity, i.e., the ability of an algorithm to react quickly to changes. Moreover, they state that an algorithm that is stable is not severely affected by changes in the environment. Competitive analysis is another, more frequently used method to measure the performance. However, one of the limitations of competitive analysis is that it is only applicable to simple versions of the DVRP. Therefore, Pillac et al. [78] propose another measure, “the value of information”. This “[…] can be interpreted as the gap between the solution returned by an algorithm A on an instance I and the solution returned by the same algorithm when all information from I is known beforehand” [78] (p. 26). On the other hand, the performance of the more advanced SDVRPs can be evaluated by a simulation model, e.g., discrete-time simulation [47]. Shen et al. [73] use Simulation of Urban Mobility (SUMO) for their performance evaluation. Furthermore, various articles describe simulation methods for the evaluation of the effectiveness of their proposed strategy in a realistic simulation environment [38,66,72,82,83,85].

6. Discussion

Clearly, there are many different approaches and methods that have been applied and tested under different circumstances and in different contexts. To the best of our knowledge, research on police patrol routing formulated as a DVRP is virtually nonexistent. This is an important knowledge gap because routine patrol is of great overall significance to daily policing and police resources are scarce and should be allocated to crime deterrent strategies that are effective [4,26]. Although there are strong parallels with studies that focus on the emergency medical services or the fire brigade, police patrol routing has its own specificities. Where the studies meet is on reacting to emergency calls and reducing response times, but they differ on the issue of preventive patrolling. Ambulances and firetrucks are not patrolling the streets in order to prevent accidents and fires, whereas police cars do patrol the streets to prevent crimes from taking place and to remind citizens of the rule of law. Despite this unique characteristic of routine police patrol, criminologists disagree on the utility of random proactive/preventive patrol. The Kansas City preventive patrol experiment [10] found out that random proactive patrol had no deterrent effect on crime. Ever since, a lot of criminologists refer to this report, but some of them also emphasize the limitations of the report: statistical, measurement and conceptual problems [36,87]. Not only the limitations affect the results in the Kansas City preventative patrol experiment, some articles even prove the opposite: random preventive patrol is one of the most important and time-consuming tasks employed on a daily basis by the police [88]. Moreover, high randomness can create a perceived omnipresence of the police and in developing routing strategies it is often mentioned as a prominent characteristic of preventative police patrol [7,8]. Therefore, an efficient and effective allocation of the available resources is crucial.

We can rely on existing measures and methods (taken from the DVRP literature, hence this review) but need to incorporate both patrolling strategies, which calls for a specific approach. This in turn raises the question of whether such a PPRP is a deterministic or stochastic DVRP. None of the articles in the review explicitly state that police patrol is stochastic but, for example, Bertsimas and van Ryzin [70] propose a model for stochastic and dynamic VRPs, in which the requests for emergency service are an example of this type of routing problem. One of their most important objectives is, just as for police patrol, reducing the wait for service. This can be done by real-time policies that are applicable in a stochastic environment [70]. In addition, Larsen et al. [12,47] acknowledge the fact that for strongly dynamic systems, the available information may be uncertain, i.e., a relatively poor quality of a priori information. This is in accordance with the classification of stochastic vehicle routing problems of Pillac et al. [11] in Section 2. Moreover, Pillac et al. [78] describe a relocation strategy, classified under dynamic and stochastic routing and refer to emergency fleet deployment. In conclusion, Ritzinger, et al. [89] examine dynamic and stochastic vehicle routing problems. They make an interesting distinction between DVRPs with stochastic travel times, with stochastic demand, with stochastic customers, or, and this is the most interesting, a DVRP with multiple stochastic aspects. In the case of police patrol routing, the travel times, as well as the customers or some other aspects can be stochastic. Up to now, only a small amount of research has been conducted on this topic [89]. Still, most of this is based on the reactive side of police patrol. Intrinsically proactive patrol does not share dynamic values to the same extent. In a static and stochastic case “the a priori route has to be determined before it is known which customers will be there or not, information which is revealed afterward” [52] (p. 7). Based on this, we can state that proactive police patrol in itself is static—the routes can be determined a priori using GIS (e.g., Route Analysis) and based on historical crime data [23]—and stochastic because of the randomness and the probability of a crime while police patrol a certain area [8,11]. The incorporation of rather dynamic reactive patrolling and static, predetermined routes (both relying on stochastic information) into one strategy, results in a dynamic and stochastic PPRP.

The solution methods that seem most convenient to address this PPRP based on this review are shown in Table 2. (Hybrid) Genetic Algorithms, routing policies and local search based on a network voronoi diagram are best suited to solve the PPRP, based on their characteristics, objectives, advantages and limitations (Table 2). GA is a powerful tool, which can perform rapid searches in large amounts of uncertain or incomplete data, with a high solving quality [66,77,80]. Parallelization and hybridization are frequently used to limit computing time and to give an exhaustive solution, respectively [66,76]. Just like with GA, traffic can also be taken into account with routing policies [12,70,71], which are also interesting for further in-depth research. The local search technique based on an NVD is adopted by Watanabe and Takamiya [64] in their article on police patrol routing. Although [64] is probably the closest to our description of police patrol, a direct link with the SDVRP is not in the article. Nevertheless, this solution method is relevant and needs further research. Approximate dynamic programming and multiple scenario approach are also interesting for the proactive part of police patrol given their predictive and preventive possibilities [78].

Furthermore, the versatility of routing problems, and the PPRP in particular, should not be neglected. Not only the routing problem is of interest but patrol beat scheduling, vehicle dispatching, fleet management and pre-emption techniques are also critical factors in developing a comprehensive police patrol routing strategy. A limitation of this review article is that interesting articles with a focus on police patrol routing strategies but lacking a focus on the (D)VRP are not included in this review. For example, Chen et al. [7] design daily patrol routes based on the ant colony algorithm, without referring to the DVRP. Given the subject of that article “designing patrol routes”, it could have been an interesting article but it is not contained in this review. Although this might be seen as a limitation, this was a deliberate choice because most of these articles do not discuss a strategy for routine police patrol, as defined in Section 2 of this article. Moreover, one of the challenges of this research is to combine all the aspects and the versatility of the PPRP into one strategy. We pursued to provide the most complete overview of the literature on this topic as possible, but we are aware of the limits and biases inherent to this literature search (e.g., additional articles or language bias).

7. Conclusions

In this review paper on the DVRP we identified the existing knowledge gaps when it comes to the PPRP. To the best of our knowledge, the PPRP is underexposed in the academic literature. Given the contemporary developments in the areas of GIS, GPS, communication and information technologies, there are a lot of opportunities for future research in studying the complex process of police patrol. The complexity of routine patrol comes from the combination of the reactive and preventative patrolling tasks of police officers. Considering the various objectives of police patrol, (cost-)efficient and effective (crime deterrent effect or spatial presence) strategies are crucial. To meet these objectives, the development of efficient routing strategies deserves more attention in future research. Moreover, the inability of previous research on the PPRP to develop a strategy for routine, motorized police patrol, without solely focusing on hot spots, in combination with major technological and methodological advancements and the remaining ambiguity regarding routine police patrol, incited us to review the literature on similar VRPs. In this paper, we classified police patrol as a stochastic and DVRP. Consequently, potentially interesting solution methods to solve the PPRP could be (hybrid) genetic algorithms, routing policies and local search based on a network voronoi diagram. (Hybrid) genetic algorithms are powerful and rapid optimization tools, which have proven their value in solving SDVRP with similar characteristics as the PPRP. Routing policies are useful because they incorporate the objective of minimizing the waiting time for a dynamic and stochastic demand pattern. Finally, the ability of the local search method to optimize initial routes when new information becomes available is in accordance with our description of the PPRP. Clearly, the “optimal” method should take account of the aforementioned characteristics. In future work we hope to report on this, using real-time data stemming from the Antwerp local police department.