Theoretical and Numerical Modeling of Acoustic Metamaterials for Aeroacoustic Applications
Abstract
:1. Introduction
2. Integral Formulation of the Problem
3. Numerical Solution
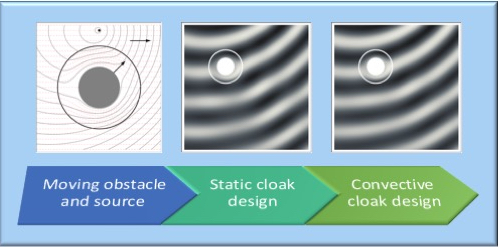
4. Effect of Motion on the Metamaterial Design
5. Results and Discussion
5.1. Effect of Convective Cloak
5.2. Boundary Impedance Estimate
5.3. Computational Efficiency
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix: The Integral Coefficients
References
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Milton, G.W.; Briane, M.; Willis, J.R. On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 2006, 8, 248. [Google Scholar] [CrossRef]
- Cummer, S.A.; Schurig, D. One path to acoustic cloaking. New J. Phys. 2007, 9, 45. [Google Scholar] [CrossRef]
- Cai, L.W.; Sánchez-Dehesa, J. Analysis of Cummer–Schurig acoustic cloaking. New J. Phys. 2007, 9, 450. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez-Dehesa, J. Anisotropic mass density by two-dimensional acoustic metamaterials. New J. Phys. 2008, 10, 023004. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez-Dehesa, J. Acoustic cloaking in two dimensions: A feasible approach. New J. Phys. 2008, 10, 063015. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez-Dehesa, J. Broadband acoustic cloaks based on the homogenization of layered materials. Wave Motion 2011, 48, 497–504. [Google Scholar] [CrossRef]
- Norris, A. Acoustic cloaking theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2411–2434. [Google Scholar] [CrossRef]
- Norris, A.N. Acoustic metafluids. J. Acoust. Soc. Am. 2009, 125, 839–849. [Google Scholar] [CrossRef] [PubMed]
- García-Meca, C.; Carloni, S.; Barceló, C.; Jannes, G.; Sánchez-Dehesa, J.; Martínez, A. Analogue transformations in physics and their application to acoustics. Sci. Rep. 2013, 3, 2009. [Google Scholar] [CrossRef] [PubMed]
- García-Meca, C.; Carloni, S.; Barceló, C.; Jannes, G.; Sánchez-Dehesa, J.; Martínez, A. Space-time transformation acoustics. Wave Motion 2014, 51, 785–797. [Google Scholar] [CrossRef]
- Visser, M. Acoustic black holes: Horizons, ergospheres and Hawking radiation. Class. Quantum Gravity 1998, 15, 1767. [Google Scholar] [CrossRef]
- Huang, X.; Zhong, S.; Stalnov, O. Analysis of scattering from an acoustic cloak in a moving fluid. J. Acoust. Soc. Am. 2014, 135, 2571–2580. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhong, S.; Liu, X. Acoustic invisibility in turbulent fluids by optimised cloaking. J. Fluid Mech. 2014, 749, 460–477. [Google Scholar] [CrossRef]
- Iemma, U.; Burghignoli, L. An integral equation approach to acoustic cloaking. J. Sound Vib. 2012, 331, 4629–4643. [Google Scholar] [CrossRef]
- Chen, H.-Y.; Yang, T.; Luo, X.-D.; Ma, H.-R. The Impedance-Matched Reduced Acoustic Cloaking with Realizable Mass and Its Layered Design. Chin. Phys. Lett. 2008, 25, 3696–3699. [Google Scholar]
- Urzhumov, Y.; Ghezzo, F.; Hunt, J.; Smith, D.R. Acoustic cloaking transformations from attainable material properties. New J. Phys. 2010, 12, 073014. [Google Scholar] [CrossRef]
- Popa, B.I.; Zigoneanu, L.; Cummer, S.A. Experimental Acoustic Ground Cloak in Air. Phys. Rev. Lett. 2011, 106, 253901. [Google Scholar] [CrossRef] [PubMed]
- Martin, P.A. Acoustic Scattering by Inhomogeneous Obstacles. SIAM J. Appl. Math. 2003, 64, 297–308. [Google Scholar] [CrossRef]
- Stevenson, R. Green’s function for the Helmholtz equation in a layered half-space. SIAM J. Appl. Math. 1990, 50, 199–215. [Google Scholar] [CrossRef]
- Morino, L.; Gennaretti, M.; Iemma, U.; Salvatore, F. Aerodynamics and Aeroacoustics of Wings and Rotors via BEM—Unsteady, Transonic and Viscous Effects. Comput. Mech. 1998, 21, 265–275. [Google Scholar] [CrossRef]
- Guo, Y. Computation of Sound Propagation by Boundary Element Method, Technical Report; Boeing Company: Huntington Beach, CA, USA, 1 September 2005.
- Agarwal, A.; Morris, P.J. Prediction Method for Broadband Noise from Unsteady Flow in a Slat Cove. AIAA J. 2006, 44, 301–310. [Google Scholar] [CrossRef]
- Myers, M.K. On the acoustic boundary condition in the presence of flow. J. Sound Vib. 1980, 71, 429–434. [Google Scholar] [CrossRef]
- Brambley, E. A Well-posed Modified Myers Boundary Condition. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010.
- Gabard, G. A comparison of impedance boundary conditions for flow acoustics. J. Sound Vib. 2013, 332, 714–724. [Google Scholar] [CrossRef]
- Morse, P.; Ingard, K. Theoretical Acoustics. In International Series in Pure and Applied Physics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Cubature (Multi-dimensional Integration). Available online: http://ab-initio.mit.edu/wiki/index.php/Cubature. (accessed on 21 May 2016).















| CPU (Year) | Op.System | WCT | WCT |
|---|---|---|---|
| Intel Xeon E5405 2.0 GHz (2007) | GNU/Linux kernel 2.6.18 | 230 | 275 |
| Intel Xeon E5520 2.2 GHz (2009) | OSX 10.11.2 | 150 | 188 |
| Intel i7 4 GHz (2015) | OSX 10.11.3 | 68 | 90 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iemma, U. Theoretical and Numerical Modeling of Acoustic Metamaterials for Aeroacoustic Applications. Aerospace 2016, 3, 15. https://doi.org/10.3390/aerospace3020015
Iemma U. Theoretical and Numerical Modeling of Acoustic Metamaterials for Aeroacoustic Applications. Aerospace. 2016; 3(2):15. https://doi.org/10.3390/aerospace3020015
Chicago/Turabian StyleIemma, Umberto. 2016. "Theoretical and Numerical Modeling of Acoustic Metamaterials for Aeroacoustic Applications" Aerospace 3, no. 2: 15. https://doi.org/10.3390/aerospace3020015
APA StyleIemma, U. (2016). Theoretical and Numerical Modeling of Acoustic Metamaterials for Aeroacoustic Applications. Aerospace, 3(2), 15. https://doi.org/10.3390/aerospace3020015