Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR
Abstract
:1. Introduction
2. Methods
2.1. The Charming QSPR & QSPR
2.2. Standardization
2.3. Outliers
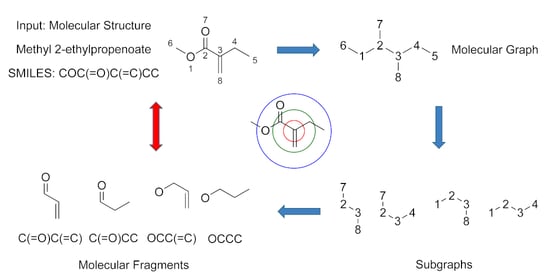
2.4. Molecular Fragment Generation and Counting
2.5. Preprocessing
2.6. Descriptor Selection
2.7. Model Training
2.8. Validation
3. Application
3.1. Example 1
3.1.1. Data Set
3.1.2. Standardization and Outlier Analysis
3.1.3. Molecular Fragment Generation, Counting, and Preprocessing
3.1.4. Descriptor Selection, Model Training, and Validation
3.2. Example 2
3.2.1. Data Set
3.2.2. Standardization and Outlier Analysis
3.2.3. Molecular Fragment Generation, Counting, and Preprocessing
3.2.4. Descriptor Selection Model Training and Validation
3.3. Example 3
3.3.1. Data Set
3.3.2. Standardization and Outlier Analysis
3.3.3. Molecular Fragment Generation, Counting, and Preprocessing
3.3.4. Descriptor Selection, Model Training, and Validation
4. Final Considerations
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Varnek, A. Tutorials in Chemoinformatics, 1st ed.; Wiley: Hoboken, NJ, USA, 2017; pp. 3–278. [Google Scholar]
- Lounkine, E.; Batista, J.; Bajorath, J. Random molecular fragment methods in computational medicinal chemistry. Curr. Med. Chem. 2008, 15, 2108–2121. [Google Scholar] [CrossRef] [PubMed]
- Ruggiu, F.; Gilles, M.; Varnek, A.; Horvath, D. ISIDA Property-Labelled Fragment Descriptors. Mol. Inform. 2010, 29, 855–868. [Google Scholar] [CrossRef] [PubMed]
- Varnek, A.; Fourches, D.; Hoonakker, F.; Solov’ev, V.P. Substructural fragments: An universal language to encode reactions, molecular and supramolecular structures. J. Comput. Aid. Mol. Des. 2005, 19, 693. [Google Scholar] [CrossRef] [PubMed]
- Baskin, I.I.; Varnek, A. Building a chemical space based on fragment descriptors. Comb. Chem. High Throughput Screen. 2008, 11, 661–668. [Google Scholar] [CrossRef] [PubMed]
- Salum, L.B.; ·Andricopulo, A.D. Fragment-based QSAR: Perspectives in drug design. Mol. Divers. 2009, 13, 277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaspar, H.A.; Baskin, I.I.; Gilles, M.; Horváth, D.; Varnek, A. GTM-Based QSAR Models and Their Applicability Domains. Mol. Inform. 2015, 34, 348–356. [Google Scholar] [CrossRef]
- Solov’Ev, V.P.; Varnek, A.; Wipff, G. Modeling of Ion Complexation and Extraction Using Substructural Molecular Fragments. J. Chem. Inf. Comput. Sci. 2000, 40, 847–858. [Google Scholar] [CrossRef]
- Varnek, A.; Fourches, A.P.D.; Horvath, D.; Klimchuk, O.; Gaudin, C.; Vayer, P.; Solov’Ev, V.P.; Hoonakker, F.; Tetko, I.; Gilles, M. ISIDA-Platform for Virtual Screening Based on Fragment and Pharmacophoric Descriptors. Curr. Comput. Drug Des. 2008, 4, 191–198. [Google Scholar] [CrossRef]
- Pirzada, S. Applications of graph theory. PAMM 2007, 7, 2070013. [Google Scholar] [CrossRef]
- Khursan, S.L.; Ismagilova, A.S.; Spivak, S.I. A graph theory method for determining the basis of ho-modesmic reactions for acyclic chemical compounds. Dokl. Phys. Chem. 2017, 474, 99. [Google Scholar] [CrossRef]
- Balaban, A.T. Applications of graph theory in chemistry. J. Chem. Inf. Model. 1985, 25, 334–343. [Google Scholar] [CrossRef]
- Manimekalai, S.; Mary, U.; Lavanya, M. Computation of topological Indices using python program for chemical graph structure. J. Phys. Conf. Ser. 2018, 1139, 012060. [Google Scholar] [CrossRef]
- Takata, M.; Lin, B.-L.; Xue, M.; Zushi, Y.; Terada, A.; Hosomi, M. Predicting the acute ecotoxicity of chemical substances by machine learning using graph theory. Chemosphere 2019, 238, 124604. [Google Scholar] [CrossRef] [PubMed]
- Ivanciuc, O. QSAR comparative study of Wiener descriptors for weighted molecular graphs. J. Chem. Inf. Comput. Sci. 2000, 40, 1412–1422. [Google Scholar] [CrossRef]
- Hayat, S.; Wang, S.; Liu, J.-B. Valency-based topological descriptors of chemical networks and their applications. Appl. Math. Model. 2018, 60, 164–178. [Google Scholar] [CrossRef]
- Randić, M.; Novič, M.; Plavšić, D. Solved and Unsolved Problems of Structural Chemistry, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 23–198. [Google Scholar]
- Randić, M. On history of the Randić index and emerging hostility toward chemical graph theory. Match Commun. Math. Comput. Chem. 2008, 59, 5. [Google Scholar]
- Balaban, A.T. Chemical Graphs: Looking Back and Glimpsing Ahead. J. Chem. Inf. Model. 1995, 35, 339–350. [Google Scholar] [CrossRef]
- Vinogradova, M.G.; Fedina, Y.A.; Papulov, Y.G. Graph theory in structure–property correlations. Russ. J. Phys. Chem. A 2016, 90, 411–416. [Google Scholar] [CrossRef]
- Dobrowolski, J.C. The structural formula version of graph theory. Match Commun. Math. Comput. Chem. 2019, 81, 527. [Google Scholar]
- Domenech, R.G.; Gálvez, J.; Ortiz, J.V.J.; Pogliani, L. Some new trends in chemical graph theory. Chem. Rev. 2008, 108, 1127. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Model. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Weininger, D.; Weininger, A.; Weininger, J.L. SMILES. 2. Algorithm for generation of unique SMILES notation. J. Chem. Inf. Model. 1989, 29, 97–101. [Google Scholar] [CrossRef]
- RDKit. Open Source Toolkit for Cheminformatics. Available online: http://www.rdkit.org (accessed on 30 October 2020).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Pret-tenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825. [Google Scholar]
- Verma, R.P.; Hansch, C. An approach toward the problem of outliers in QSAR. Bioorganic Med. Chem. 2005, 13, 4597–4621. [Google Scholar] [CrossRef]
- Kim, K.H. Outliers in SAR and QSAR: Is unusual binding mode a possible source of outliers? J. Comput. Mol. Des. 2007, 21, 63–86. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Rasulev, B.F.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. Coral: QSPR modeling of rate constants of reactions between organic aromatic pollutants and hy-droxyl radical. J. Comput. Chem. 2012, 33, 1902–1906. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Rasulev, B.F.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. QSAR models for ACE-inhibitor activity of tri-peptides based on representation of the molecular struc-ture by graph of atomic orbitals and smiles. Struct. Chem. 2012, 23, 1873–1878. [Google Scholar] [CrossRef]
- Benfenati, E.; Toropov, A.; Toropova, A.P.; Manganaro, A.; Diaza, R.G. coral Software: QSAR for Anticancer Agents. Chem. Biol. Drug Des. 2011, 77, 471–476. [Google Scholar] [CrossRef]
- Sklearn.linear_model.Lasso—Scikit-Learn 0.23.2 Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html (accessed on 30 October 2020).
- Feature Selection—Scikit-Learn 0.23.2 Documentation. Available online: https://scikit-learn.org/stable/modules/feature_selection.html#l1-feature-selection (accessed on 30 October 2020).
- Feature Selection Using SelectFromModel and LassoCV—Scikit-Learn 0.23.2 Documentation. Available online: https://scikit-learn.org/stable/auto_examples/feature_selection/plot_select_from_model_diabetes.html#sphx-glr-auto-examples-feature-selection-plot-select-from-model-diabetes-py (accessed on 30 October 2020).
- Alexander, D.L.J.; Tropsha, A.; Winkler, D.A. Beware of R2: Simple, Unambiguous Assessment of the Prediction Accuracy of QSAR and QSPR Models. J. Chem. Inf. Model. 2015, 55, 1316–1322. [Google Scholar] [CrossRef] [Green Version]
- Tropsha, A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef]
- Gramatica, P.; Sangion, A. A historical excursus on the statistical validation parameters for QSAR models: A clarification concerning metrics and terminology. J. Chem. Inf. Model. 2016, 56, 1127. [Google Scholar] [CrossRef]
- Schultz, T.W.; Netzeva, T.I. Development and evaluation of QSARs for ecotoxic endpoints: The ben-zene response-surface model for Tetrahymena toxicity. In Modeling Environmental Fate and Toxicity; Cronin, M.T.D., Livingstone, D.J., Eds.; CRC Press: Boca Raton, FL, USA, 2004; Volume 4, Chapter 12; pp. 265–284. [Google Scholar]
- Zhu, H.; Tropsha, A.; Fourches, D.; Varnek, A.; Papa, E.; Gramatica, P.; Oberg, T.; Dao, P.; Cherkasov, A.; Tetko, I.V. Combinatorial QSAR Modeling of Chemical Toxicants Tested against Tetrahymena pyriformis. J. Chem. Inf. Model. 2008, 48, 766. [Google Scholar] [CrossRef] [Green Version]
- The IUPAC Stability Constants Database, SC-Database (No Longer Available Commercially) and Mini-SCDatabase. Available online: http://www.acadsoft.co.uk/scdbase/scdbase.htm (accessed on 30 October 2020).
- Solov’ev, V.P.; Tsivadze, A.Y.; Varnek, A. A New approach for accurate QSPR modeling of metal complexation: Application to stability constants of complexes of lanthanide ions Ln3+, Ag+, Zn2+, Cd2+, and Hg2+ with organic ligands in water. Macroheterocycles 2012, 5, 404. [Google Scholar] [CrossRef] [Green Version]
- Horvath, D.; Bonachera, F.; Solov’Ev, V.P.; Gaudin, C.; Varnek, A. Stochastic versus Stepwise Strategies for Quantitative Structure−Activity Relationship GenerationHow Much Effort May the Mining for Successful QSAR Models Take? J. Chem. Inf. Model. 2007, 47, 927–939. [Google Scholar] [CrossRef]
- Solov’ev, V.P.; Varnek, A. Anti-HIV activity of HEPT, TIBO, and cyclic urea derivatives: Structure-property studies, focused combinatorial library Generation, and hits selection using substructural mo-lecular fragments method. J. Chem. Inf. Comput. Sci. 2003, 43, 1703–1719. [Google Scholar]












| Software | R2-Train | MAE-Train | MAE-Test | R2-Test | |
|---|---|---|---|---|---|
| CHARMING | LASSO | 0.880 | 0.267 | 0.385 | 0.783 |
| SVM | 0.904 | 0.215 | 0.389 | 0.784 | |
| GBM | 0.989 | 0.134 | 0.462 | 0.706 | |
| RF | 0.963 | 0.150 | 0.431 | 0.723 | |
| RF-Stck | 0.897 | 0.224 | 0.398 | 0.769 | |
| Linear-Ens. | 0.924 | 0.191 | 0.360 | 0.799 | |
| Multilinear | 0.900 | 0.240 | 0.403 | 0.775 | |
| ZHU’s work | kNN-Dragon | 0.92 | 0.22 | 0.27 | 0.85 |
| kNN-MolconnZ | 0.91 | 0.23 | 0.30 | 0.84 | |
| SVM-Dragon | 0.93 | 0.21 | 0.31 | 0.81 | |
| SVM-MolconnZ | 0.89 | 0.25 | 0.30 | 0.83 | |
| ISIDA-kNN | 0.77 | 0.37 | 0.36 | 0.73 | |
| ISIDA-SVM | 0.95 | 0.15 | 0.32 | 0.76 | |
| ISIDA-MLR | 0.94 | 0.20 | 0.31 | 0.81 | |
| CODESSA-MLR | 0.72 | 0.42 | 0.44 | 0.71 | |
| OLS | 0.86 | 0.30 | 0.35 | 0.77 | |
| PLS | 0.88 | 0.28 | 0.34 | 0.81 | |
| ASNN | 0.83 | 0.31 | 0.28 | 0.87 | |
| PLS-IND | 0.76 | 0.39 | 0.39 | 0.74 | |
| MLR-IND | 0.77 | 0.39 | 0.40 | 0.75 | |
| ANN-IND | 0.77 | 0.39 | 0.39 | 0.76 | |
| SVM-IND | 0.79 | 0.31 | 0.35 | 0.79 |
| R2-Train | RMSE-Train | RMSE-Test | R2-Test | K | ||
|---|---|---|---|---|---|---|
| LASSO | 0.951 | 1.067 | 1.197 | 0.949 | 0.981 | 1.011 |
| SVM | 0.963 | 0.926 | 1.325 | 0.941 | 0.976 | 0.976 |
| GBM | 0.994 | 0.728 | 1.918 | 0.86 | 0.95 | 0.937 |
| RF | 0.985 | 0.592 | 1.214 | 0.945 | 0.98 | 0.967 |
| RF-Stk | 0.956 | 1.008 | 1.198 | 0.947 | 0.981 | 1.010 |
| Linear-Ens. | 0.967 | 0.861 | 1.368 | 0.936 | 0.975 | 0.992 |
| Multilinear | 0.964 | 0.894 | 1.378 | 0.939 | 0.975 | 1.001 |
| Set | Model | RMSE-Train | R2-Train | RMSE-Test | R2-Test | K | |
|---|---|---|---|---|---|---|---|
| CU | LASSO | 0.310 | 0.949 | 0.600 | 0.874 | 0.996 | 1.022 |
| SVM | 0.335 | 0.941 | 0.442 | 0.843 | 0.998 | 1.009 | |
| GBM | 0.210 | 0.993 | 0.949 | 0.483 | 0.993 | 0.928 | |
| RF | 0.277 | 0.963 | 0.629 | 0.661 | 0.996 | 0.968 | |
| RF-Stk. | 0.460 | 0.884 | 0.594 | 0.878 | 0.996 | 0.972 | |
| Linear-Ens. | 0.402 | 0.912 | 0.419 | 0.796 | 0.998 | 0.995 | |
| Multilinear | 0.244 | 0.966 | 0.863 | 0.832 | 0.992 | 1.031 | |
| HEPT | LASSO | 0.292 | 0.954 | 0.918 | 0.837 | 0.990 | 1.065 |
| SVM | 0.303 | 0.951 | 0.847 | 0.798 | 0.991 | 1.053 | |
| GBM | 0.275 | 0.976 | 0.434 | 0.889 | 0.997 | 0.972 | |
| RF | 0.258 | 0.966 | 0.330 | 0.948 | 0.999 | 0.974 | |
| RF-Stk. | 0.311 | 0.948 | 0.337 | 0.945 | 0.998 | 1.018 | |
| Linear-Ens. | 0.291 | 0.954 | 0.937 | 0.792 | 0.989 | 1.062 | |
| Multilinear | 0.265 | 0.962 | 1.071 | 0.844 | 0.987 | 1.078 | |
| TIBO | LASSO | 0.529 | 0.858 | 0.868 | 0.687 | 0.976 | 1.018 |
| SVM | 0.474 | 0.88 | 0.869 | 0.681 | 0.976 | 1.012 | |
| GBM | 0.348 | 0.951 | 0.721 | 0.797 | 0.983 | 1.011 | |
| RF | 0.365 | 0.930 | 0.657 | 0.822 | 0.986 | 1.012 | |
| RF-Stk | 0.564 | 0.832 | 1.114 | 0.506 | 0.962 | 1.023 | |
| Linear-Ens. | 0.493 | 0.873 | 0.874 | 0.681 | 0.975 | 1.009 | |
| Multilinear | 0.405 | 0.910 | 0.969 | 0.641 | 0.969 | 0.992 |
| Set | N-Train | R2-Train | N-Test | R2-Test | |
|---|---|---|---|---|---|
| CHARMING | TIBO | 65 | 0.93 | 8 | 0.822 |
| HEPT | 75 | 0.966 | 9 | 0.948 | |
| CU | 83 | 0.949 | 10 | 0.874 | |
| ISIDA | TIBO | 66 | 0.885 | 7 | 0.943 |
| HEPT | 76 | 0.941 | 8 | 0.887 | |
| CU | 84 | 0.885 | 9 | 0.845 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, P.C.S.; Evangelista, J.S.; Leal, I.; Miranda, P.C.M.L. Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR. Mathematics 2021, 9, 60. https://doi.org/10.3390/math9010060
Costa PCS, Evangelista JS, Leal I, Miranda PCML. Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR. Mathematics. 2021; 9(1):60. https://doi.org/10.3390/math9010060
Chicago/Turabian StyleCosta, Paulo C. S., Joel S. Evangelista, Igor Leal, and Paulo C. M. L. Miranda. 2021. "Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR" Mathematics 9, no. 1: 60. https://doi.org/10.3390/math9010060
APA StyleCosta, P. C. S., Evangelista, J. S., Leal, I., & Miranda, P. C. M. L. (2021). Chemical Graph Theory for Property Modeling in QSAR and QSPR—Charming QSAR & QSPR. Mathematics, 9(1), 60. https://doi.org/10.3390/math9010060