1. Introduction
The effect of home advantage is important in modeling the probabilities of the results of sports matches. These probabilities are the basis for listing odds for sports matches and therefore it is important for betting companies to have a good model for their estimation. Since the probabilities of the results of sports matches are not known (unlike, for example, in roulette), bookmakers are exposed to the risk of loss. The risk can be reduced by increasing their margin, but this reduces the competitiveness of bookmakers. Recent study of margins in English football leagues can be found in (
Marek 2018) and it shows that bookmakers have significantly reduced margins in recent years. Next, results of (
Buhagiar et al. 2018) show “that bettors lose more on events that are more accurately predicted by bookmakers”. Therefore, it is important to cover all available aspects that can improve the bookmakers’ models. This article is focused on one important factor—home advantage.
Home advantage in sports is addressed by many researchers. The main causes of the home advantage—crowd effect, referee bias, travel effect, familiarity with local conditions, territoriality, special tactics, etc.—are analysed and discussed in detail by (
Pollard and Gómez 2014), and the scientific interest in this area can be tracked back to (
Schwartz and Barsky 1977). Exhaustive studies about home advantage can be found in (
Allen and Jones 2014) and (
Pollard and Pollard 2005). In both papers, as well as in many others, the home advantage of a league is based on comparing the number of points that were earned at home grounds with the total number of points that were awarded. This approach, proposed by (
Pollard 1986), is straightforward, easy to use, and produces reasonable results for a league as a whole. Adjustment that is required when the approach is used for individual teams is described in (
Pollard and Ruano 2009); nevertheless, this procedure requires data over several seasons.
All papers mentioned in the previous paragraph understand home advantage similarly as defined in (
Pollard and Pollard 2005): “the number of points obtained by the home team expressed as a percentage of all points obtained in all games played”. However, this definition can be problematic in some situations, e.g., let us assume that two teams
A and
B played each other exactly two times in a season. Team
A recorded 4–0 win at its home ground and 2–0 win away from home. When points are used in this situation we conclude that the team
A won exactly half of its points at its home ground. This leads to a conclusion that the team
A does not have home advantage. However, using the difference of goals scored and conceded—for the team
A: four goals at its home ground and two goals away from home—indicates that the team
A recorded better result (measured only by the goal difference) at the home ground, i.e., it has the home advantage. The team
B lost by two goals at its home ground and by four goals away from home. As in the case of the team
A, the result at its home ground was better. If the similar situation happens often in a league then analysis may end with a conclusion that the home advantage—understood in its natural meaning—does not exist, or the home advantage can be underestimated.
The solution of this problem can be in using goals instead of points. This provides a deeper view of the home advantage problem, and it is closer to the natural meaning of the home advantage, i.e., better performance, not only more points. There are several approaches how to deal with goals, the first approach—based on modelling team ability and home advantage—was used by (
Clarke and Norman 1995) for the analysis of home advantage of individual clubs in English football leagues. These models can be tracked back to (
Maher 1982) and are usually used to predict match outcomes in football and other sports, e.g., (
Karlis and Ntzoufras 2003) in water polo, (
Marek et al. 2014) in ice hockey. Next approach is presented by (
Goumas 2017) who models home advantage for individual teams in UEFA Championship League. His method is based on ratio of goals that was scored by the team at its home ground and total number of goals scored at its home ground, i.e., goals that the home team scored and conceded at its home ground. The third approach, on which this paper builds, was proposed by (
Marek and Vávra 2017), and it uses a combined measure of home advantage that takes into account results (goals scored and conceded) of two same teams in one season, once at the home ground and once at the away team ground. The number of goals scored and conceded was successfully used in another type of analysis, e.g., (
Hassanniakalager and Newall 2019) who analysed the potential variation in soccer betting outcomes—they used the cumulative number of points earned and the number of goals scored and conceded over the previous five matches.
The approach presented in this paper allows evaluation of home advantage for a single team in one season. It can also be used to evaluate home advantage of larger groups of data: league in one season, league over several seasons, and one team over several seasons. The price for this advantage is that only leagues with a balanced schedule can be analysed; nevertheless, this is the most common type of schedule in association football, and all leagues analysed in this paper use it.
The following parts present definition of home advantage based on goals scored and conceded. It uses three-state random variable that describes home advantage of a given object of interest: a team in a single season, a team over several seasons, a league in one season, and a league over several seasons. The main goals of this paper are to offer a usable procedure based on goals scored and conceded for evaluation of home advantage and procedure for identification of objects—leagues or teams—with similar type of home advantage. Leagues from the following countries are analysed in this paper: Belgium, the Czech Republic, England, France, Germany, Greece, Italy, Netherlands, Portugal, Spain, and Turkey (for some countries, even the lower level leagues are used). The 2015/2016 season of the top-level leagues of similar countries was analysed using method based on points in (
Leite 2017), and it can be used for comparison of results.
2. Data
Leagues used in this paper are:
Belgium: Belgian First Division A (level 1, );
Czech Republic: Czech First League (level 1, );
England: Premier League (level 1, ), English Football League Championship (level 2, ), English Football League One (level 3, ), English Football League Two (level 4, ), and National League (level 5, );
France: Ligue 1 (level 1, ) and Ligue 2 (level 2, );
Germany: Bundesliga (level 1, ) and 2. Bundesliga (level 2, );
Greece: Superleague Greece (level 1, );
Italy: Serie A (level 1, ) and Serie B (level 2, );
Netherlands: Eredivisie (level 1, );
Portugal: Primeira Liga (level 1, );
Spain: La Liga (level 1, ) and Segunda Divisíon (level 2, );
Turkey: Süper Lig (level 1, ).
All results starting 2007/2008 season and ending 2016/2017 season are used in the analysis. These results were obtained from (
Football-Data.co.uk 2018) and (
HETliga.cz 2018). Official websites of leagues e.g.,
LaLiga.es (
2018) were used for basic data check, and to identify awarded wins
1 which, obviously, do not represent abilities of teams. The whole of the 2014/2015 season of
was excluded from the analysis because of too many awarded wins. Awarded wins were also recorded in the following matches: Trabzonspor vs. Sivasspor (2007/2008,
), Belenenses vs. Naval (2007/2008,
), Bohemians 1905 vs. Bohemians Praha (2009/2010,
), Gaziantepspor vs. Bursaspor (2010/2011,
), Bursaspor vs. Besiktas (2010/2011,
), Aris vs. Tripolis (2011/2012,
), Panathinaikos vs. Olympiakos (2011/2012,
), AEK vs. Panthrakikos (2012/2013,
), Besiktas vs. Galatasaray (2013/2014,
), Trabzonspor vs. Fenerbahce (2013/2014,
), Blackpool vs. Huddersfield (2014/2015,
), Panathinaikos vs. Olympiakos (2015/2016,
), Bastia vs. Lyon (2016/2017,
), and Sassuolo vs. Pescara (2016/2017,
). These matches were excluded from the analysis. Opposite matches between mentioned teams were also excluded as the analysis requires to have both matches played. The rest of the 72,182 matches were used in the analysis.
3. Methods
Three types of measures are defined in (
Marek and Vávra 2017): active measure of home advantage (it uses difference between goals scored at home and away from home); passive measure of home advantage (it uses difference between goals conceded at home and away from home); and combined measure of home advantage (it uses both goals scored and conceded) which is used in this paper and described in Definition 1.
Definition 1. Combined measure of home advantage is random variable C that can take values , and 1. for team if two matches between teams and in a season ended with a better result – measured by goal differences in matches – for team away from home (at ’s ground). for team if goal differences in both matches were exactly the same from ’s point of view, and for team if this team recorded better result – measured by goal differences in matches – at its own ground. With results at the home ground of team and at the home ground of team the value of random variable C for team is determined as 3.1. Parameters Estimation Method
A balanced schedule was used in all leagues and seasons, i.e., each team played every other team exactly twice in a season, once at home and once away from home. The combined measure of home advantage combines results of the first half of the season (team A plays at its home ground against team B) with results of the second half of the season (team A plays against team B at B’s home ground). This means that 72,182 matches offers 36,091 observations of combined measure of home advantage.
Let
are random variables which describe number of cases (e.g., for a team in a season) where it is possible to identify home advantage (
), away advantage (
), and no advantage (
), i.e.,
sums number of cases where
. Vector
follows trinomial distribution with parameters
, and
K with probability function
where
K is total number of observations of combined measure in a season,
are probabilities of occurring home advantage (
), away advantage (
), and no advantage (
).
(
) are observations of appropriate advantage.
Maximum likelihood estimator of parameters
is
The procedure is demonstrated on results of
(Belgian First Division A) and
(La Liga) in the 2016/2017 season.
Table 1 contains observed counts for combined measure and
Table 2 contains point estimates of parameters
.
3.2. Comparison Methods
Home advantages of leagues were compared by two approaches. The first approach is based on Jeffrey divergence (
), i.e., symmetric version of Kullback–Leibler distance. Jeffrey divergence (described in detail in (
Deza and Deza 2006, p. 185)) can be used to measure distance between two probability distributions
P and
Q as
Equation (
4) is used to measure distance between probability distributions of
for each two leagues or teams. Obtained distances are compared to find leagues or teams with home advantage that is similar (or different). Values of
are multiplied by 100 for better readability. For the data presented in
Table 2 we obtain 100·
JD = 9.410.
The second approach is based on the test for homogeneity of parallel samples that allows to test hypothesis
: two samples come from the same population (or in this case: that home advantage in both tested leagues, or for both tested teams, is described by the same distribution) against alternative hypothesis
: two samples do not come from the same population (or in this case: that home advantage in both tested leagues, or for both tested teams, is described by different distributions).
statistic can be computed for a case with two leagues or two teams as
where appropriate observed numbers (
etc.) are obtained according to
Table 3.
Asymptotical distribution of
statistic for the data in
Table 3 is
distribution with two degrees of freedom. For more details on this test see (
Rao 2002, pp. 398–402).
Value of
for the data in
Table 1 is 6.378, and corresponding
p-value is 0.094. The hypothesis
that home advantage in
(Belgian First Division A) and
(La Liga) in the 2016/2017 season is described by the same distribution cannot be rejected, i.e., the null hypothesis that there is no difference in the home advantage (measured by the combined measure) in
and
in the 2016/2017 season cannot be rejected.
The method based on statistic can be used to test whether the home advantage in two leagues, or of two teams, differ or not. Next, both presented methods may be used as a heuristic procedure to identify groups of leagues, or teams, with similar home advantage. The steps of the procedure are:
- (1)
Construct a graph, where leagues are used as vertices and distances (measured by or ) are used as edges;
- (2)
Find the edge with the highest distance and remove it from the graph;
- (3)
Repeat step until the graph becomes disconnected, i.e., until two components are obtained.
This heuristic procedure will determine two groups (components) of leagues, or teams, where distance ( or ) between any league, or team, from the first group (component) and the second group (component) is always equal or greater than the last removed distance of the graph. The described procedure can continue to obtain more components.
4. Results
The first subsection will present the results obtained if only categorization by leagues is used, i.e., for each analysed league over whole 10 seasons. The second subsection will present major findings for single seasons, and the last subsection will demonstrate usage of this approach for single teams.
4.1. Categorization by Leagues
All findings in this chapter are valid for leagues over the last 10 seasons together (observed counts of combined measure in each season are connected together for each league to obtain one group of data for a league).
Observed counts of combined measure for each analysed league over all 10 seasons (from the 2007/2008 season to the 2016/2017 season) are presented in
Table 4.
The highest and lowest value of each column of estimated probabilities are highlighted. Test of hypothesis that home advantage exists can be tested by the procedure described in (
Marek and Vávra 2017). The result of this test is that the null hypothesis about non-existent home advantage can be rejected, and the alternative hypothesis that home advantage exists can be accepted for all leagues in
Table 4. The main goal of this paper is to build on these expected results, and to compare home advantage of leagues.
Each two leagues can be compared using the test for homogeneity of parallel samples described in
Section 3.2. All
p-values for each pair of the highest leagues of each country are listed in
Table 5. In the case of
, the hypothesis that home advantage is described by the same distribution cannot be rejected only in the case of testing with
. Nevertheless, if all 19 leagues are taken into account, then the only league where tests against any other league result in conclusion that null hypothesis can be rejected, and the alternative that home advantage in both tested leagues is described by different distributions, is
.
(
Leite and Pollard 2018) compared differences in home advantage between level 1 and level 2 football leagues. They used data between the 2010/2011 season and the 2016/2017 season, i.e., similar data as used in this paper. Their analysis used method based on points gained, and they found out that in England, Germany, Spain, Italy, and France no difference in home advantage was recorded. To compare results, we performed the analysis for the same seasons. Obtained results are the same with one exception—Spain. In Spain, according to our analysis, the home advantage is different in both leagues with interpretation that in
the home advantage is higher. This indicates, that method based on combined measure can offer more detailed view of home advantage, and it is able to find differences that cannot be identified by some methods based on points.
The second approach of comparing is not based on testing but on measuring distance between distributions that describe home advantage. Jeffrey divergence (multiplied by 100) measures distances between each pair of leagues, and selected results are shown in
Table 6. The highest value among all analysed leagues is recorded for
and
where
, and the lowest value is recorder for
and
where
.
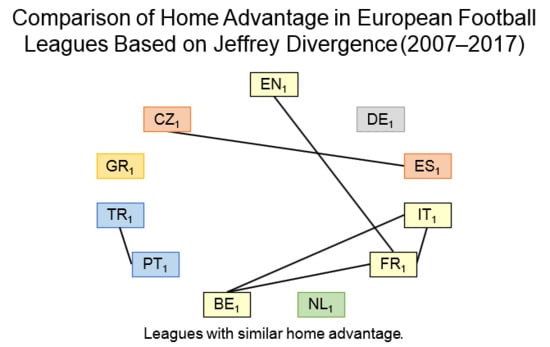
The procedure described in
Section 3.2 is used to identify groups of leagues with similar home advantage, i.e., a graph where vertices represent leagues, and edges represent distances between leagues is constructed; edges with the highest distances are removed until a disconnected graph is obtained. The last removed edge is between
and
(
). After this, the graph contains two components, one with
and the second one with the remaining 18 leagues. As can be seen from
Table 4,
shows a stronger home advantage than all the other leagues (parameter
). When the removing continues, the third component containing
is obtained; as can be seen from
Table 4,
has the lowest home advantage. This procedure can continue further. Summary of all consequently obtained components is
The other six leagues , , , , , and are in the largest component. The next removed distance would divide previously obtained components. Leagues in each group can be considered as those that poses similar home advantage.
The procedure based on statistics offers exactly the same results. The only difference is sequence of obtained components (e.g., the first obtained component is ). In the case of statistics, the removed distance can be also connected with appropriate p-value from the test for homogeneity of parallel samples. As stated before, the first component contains , and it is obtained when the edge between and is removed. The value of statistics is 6.674 and corresponding p-value is 0.048 (i.e., the difference is still statistically significant at the 0.05 level of significance). The next component is obtained when edge between and is removed. Corresponding p-value of this edge is 0.173. This means that the difference in home advantage for these two leagues cannot be considered as statistically significant at the 0.05 level of significance. However, as stated before, it is possible to use this approach as a heuristic procedure for identification of leagues with similar home advantage.
4.2. Categorization by Leagues and Seasons
In the previous subsection, the highest difference in home advantage was identified between
and
(e.g., see
Table 4); therefore,
and
are selected to present evolution of
during all 10 seasons in
Figure 1. The next league chosen for the presentation of results is
that recorded the lowest value of
(see
Table 4).
Point estimates
of
are in all seasons (with an exception of 2015/2016 season that was excluded from the analysis; see
Section 2) above the point estimates
of
and usually above the point estimates
of
. The test for homogeneity of parallel samples described in
Section 3.2 can be used to identify differences in home advantage between leagues in single seasons.
As an example, the test is used for each pair of leagues presented in
Figure 1:
The hypothesis that home advantage in and is described by the same distribution cannot be rejected in five seasons: 2008/2009, 2009/2010, 2010/2011, 2011/2012, and 2012/2013. The hypothesis can be rejected, and the alternative hypothesis that home advantage in and is described by different distributions can be accepted in four seasons: 2007/2008, 2013/2014, 2015/2016, and 2016/2017.
The same test used for and shows that can be rejected, and can be accepted in three seasons: 2009/2010, 2010/2011, and 2013/2014 (the main difference in the 2010/2011 season is in values of and ). cannot be rejected in the rest six seasons.
The third tested pair is and for which can be rejected, and can be accepted in three seasons: 2007/2008, 2015/2016, and 2016/2017. cannot be rejected in the rest of the seven seasons.
Previous results suggest that when using data for a single season, the difference in home advantage between leagues must be substantial, otherwise it will not be identified. Therefore, to identify groups of leagues with similar home advantages, the heuristic procedure described in
Section 3.2 will be used.
Table 7 contains, for each season analysed, the first two components identified by this procedure (distance was measured by
statistic, see Equation (
5)), e.g., the first of two obtained components in the 2007/2008 season contains
and
, and the second component contains all other leagues. The interpretation of these results is based on values of
—the first component includes leagues for which the
values are higher than for the leagues forming the second component.
Table 7 contains one remark (
) for the 2009/2010 season. The interpretation in this season is not made in favour of the higher or lower home advantage, because the different value (0.29) is obtained for
which is the highest value for all leagues not only in this season but also in all tested seasons.
The 2015/2016 season of
,
,
,
,
,
,
,
,
, and Russia was analysed in (
Leite 2017) with the result that home advantage can be found in each of these leagues. Except for Russia, this paper contains all leagues that were analysed in (
Leite 2017). The same approach as in (
Leite 2017) was used to compute home advantage based on points for all 19 leagues used in this paper. Except for
, all leagues can be considered to have home advantage based on points. When the combined measure that uses goals scored and conceded is used, and home advantage is tested by the procedure described in (
Marek and Vávra 2017), then the result is the same, i.e., the null hypothesis about non-existent home advantage cannot be rejected only for
.
Nevertheless, the interpretation of results based on obtained values is different, e.g., three teams with the highest home advantage based on points are , , and . The approach presented in this paper provides more detailed view of home advantage (based on combined measure)—it offers the same interpretation for and , however in the case of the home advantage is below average of all 19 leagues, and high value is obtained for the parameter (no advantage), i.e., the same difference at home and away.
This illustrates that both methods will probably answer the question about existence of home advantage in the similar way. The main difference is in the interpretation how strong is the home advantage and in the possibility of better understanding of home advantage.
Complete results for point estimate
are contained in
Table 8. The table uses a tint to emphasize the values—the darker the higher the value of the
. These results can be used to assess whether or not there are large differences over the years in a single league. As we have seen before in
Figure 1, the results can change significantly over the time. Stable results can be seen in
and
. Big variance can be seen in
and
. This information can be used by bookmakers and gamblers to identify leagues where home advantage plays significant role each year.
4.3. Home Advantage for Single Teams
Out of all leagues, the most surprising results were obtained for
; therefore, it is chosen for demonstration of proposed approach for single teams. Again, as for leagues, it can be used over several seasons or even for a single season. The lowest recorded home advantage for
was in the 2015/2016 season; therefore, because it can offer a detailed view of home advantage of teams in this season, it is chosen for the demonstration of usage for single teams in a single season. Results are presented in
Table 9. Strong home advantage can be identified only for two teams—Barnet and York. Totally,
for 10 out of 24 teams,
for 9 out of 24 teams, and
for 5 out of 24 teams. These results demonstrate that surprising results about home advantage in
in the 2015/2016 season is not caused by several teams but, on the contrary, it is common for almost all teams.
Each two teams can be compared using the test for homogeneity of parallel samples described in
Section 3.2. The team with the highest number of cases where the null hypothesis that home advantage of both tested teams is described by the same distribution can be rejected, and the alternative that home advantage of both tested teams is described by different distributions can be accepted is Luton. For Luton, 9 out of 23 teams can be considered as those with statistically significant difference in home advantage. The next team with most differences is Barnet with four cases.
The heuristic procedure based on searching for components of graph (see
Section 3.2) can be used to identify groups of teams with similar home advantages. When distances are based on Jeffrey divergence, then the first obtained component is Luton with interpretation that it has lower home advantage. Next obtained components are: Barnet (higher home advantage), York (higher home advantage), AFC Wimbledon and Wycombe (lower home advantage), Hartlepool (higher home advantage), etc.
5. Conclusions
This paper described procedures based on combined measure of home advantage that can be used to compare home advantage of different leagues. Combined measure of home advantage is based on both goals scored and conceded, and this is the reason why it can detect home advantage in a better way than the usual approach based on points gained.
Section 3.2 introduced two methods that can be used to compare home advantage. The first method is based on classical hypothesis testing, and the second method uses distances between leagues and heuristic procedure that can be used to find leagues with similar home advantage.
Described procedures were used in 10 seasons in 19 football leagues, and obtained results were compared. Results for all seasons together were used in
Section 4.1; the Superleague Greece (
) was identified as a league with the highest home advantage, and the English Football League Two (
) was identified as a league with the lowest home advantage. Based on the results in the lower level leagues, we can formulate a hypothesis that home advantage is lower in the lower level leagues (see
Table 4) and that it can be caused by lower attendance that has lower influence on the referee—a generally accepted idea. In further research, therefore, our method could be used to test this hypothesis. The results of matches where, due to the COVID-19 pandemic, limited audience is allowed, could be used for this purpose. However, in order to use our method, it is necessary to play whole season with this limitation.
Section 4.2 showed that when using data for a single season, the difference in home advantage between leagues must be substantial to prove statistically significant difference; for this case, to identify groups of leagues with similar home advantages, the heuristic procedure defined in
Section 3.2 can be used. Finally,
Section 4.3 demonstrates usage for single teams.
The results of this paper can help bookmakers identify leagues and teams where home advantage plays a significant role. As a result, bookmakers can improve their prediction models and become more competitive by being able to reduce margins and not increase risk. For gamblers, the results offer the opportunity to identify leagues and teams with a stable home advantage and, knowing the result of the first match between the two teams, to have information available for betting on the return match.