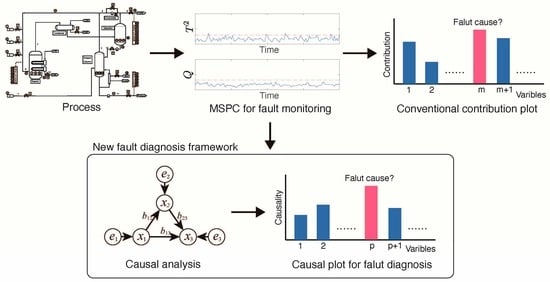
Causal Plot: Causal-Based Fault Diagnosis Method Based on Causal Analysis

Abstract

Fault diagnosis is crucial for realizing safe process operation when a fault occurs. Multivariate statistical process control (MSPC) has widely been adopted for fault detection in real processes, and contribution plots based on MSPC are a well-known fault diagnosis method, but it does not always correctly diagnose the causes of faults. This study proposes a new fault diagnosis method based on the causality between process variables and a monitored index for fault detection, which is referred to as a causal plot. The proposed causal plot utilizes a linear non-Gaussian acyclic model (LiNGAM), which is a data-driven causal inference algorithm. LiNGAM estimates a causal structure only from data. In the proposed causal plot, the causality of a monitored index of fault detection methods, in addition to process variables, is estimated with LiNGAM when a fault is detected with the monitored index. The process variables having significant causal relationships with the monitored indexes are identified as causes of faults. In this study, the proposed causal plot was applied to fault diagnosis problems of a vinyl acetate monomer (VAM) manufacturing process. The application results showed that the proposed causal plot diagnosed appropriate causes of faults even when conventional contribution plots could not do the same. In addition, we discuss the effects of the presence of a recycle flow on fault diagnosis results based on the analysis result of the VAM process. The proposed causal plot contributes to realizing safe and efficient process operations.

1. Introduction

Fault detection is a crucial technique in process operations for maintaining product quality and process safety [1,2]. Process monitoring methods based on machine learning have widely been used in many processes. Although a fault should be recovered swiftly, to manually identify causes of the fault in a short amount of time is difficult, even if the fault is appropriately detected shortly after its occurrence [3]. A precise method for diagnosing causes of faults is needed for realizing a stable and efficient process operation. Thus, this study focuses not on fault detection but rather on fault diagnosis.

A contribution plot based on multivariate statistical process control (MSPC) has been proposed for fault diagnosis [4]. MSPC is a widely-adopted fault detection framework based on process data, which detect faults that cannot be detected by monitoring each variable independently, by considering the relationship among process variables. The $T^2$ and Q statistics are used as the monitored indexes, and a fault is detected when either $T^2$ or Q statistic exceeds their predefined control limit. In the contribution plot, process variables with significant contributions to the $T^2$ or Q statistic are judged as the causes of the fault.

The contribution plots have been widely used in various processes and their usefulness has been confirmed through real applications [5,6]. However, Yoon et al. indicated that causes of faults are not always diagnosed with a conventional contribution plot, even in simple processes [7]. They showed examples in which contribution plots could not correctly identify the causes of faults with a CSTR-type reactor, which suggested that prior knowledge about the process and its control systems are necessary for appropriate fault diagnosis. Westerhuis et al. discussed the possibility that a fault increases the contributions of process variables unrelated to the fault cause in addition to variables directly related to the fault cause, since residuals between the PCA model and the original process data may be computationally distributed to various variables other than the variable related to the fault cause [8].

Fault identification frameworks based on the Bayesian network (BN) have been proposed [9,10]. Although BN-based methods require prior knowledge of structural relationships among process variables before constructing the model, such relationships are not always known.

Causality should be considered when the causes of a fault are analyzed. Causality means a stronger relationship than contribution because it explains the cause and the effect. Fault diagnosis methods based on the causality of process variables have been proposed, in which Granger causality is adopted for estimation of causality [11,12,13]. The Granger causality (GC) is a causal analysis method for time series data, which determines whether variable Y can be predicted by variable X [14]. GC may reach wrong conclusions when three or more variables are confounded because it uses a t-test or an F test for causal tests between possible pairs of two variables. The causality among three or more variables should be considered for fault diagnosis because multiple process variables may be simultaneously altered due to faults.

This study proposes a new causality-based fault identification method that can handle causality among three or more variables. The proposed method estimates the causal effects of process variables on the monitored indexes of fault detection methods, which is referred to as a causal plot.

A linear non-Gaussian acyclic model (LiNGAM) [15], which is a machine learning technique for causal inference [16], is used for calculating the causal plot. In LiNGAM, the causal structure among measured variables can be estimated from data alone, even when prior knowledge about the process is not available. LiNGAM can avoid problems in BN-based and GC-based methods, i.e., that the causal structure among the process variables must be known before analysis, and can be applied to multivariate processes having three or more process variables.

In the proposed causal plot, the causality of the monitored indexes of fault detection methods, in addition to process variables, is estimated by means of LiNGAM. Process variables with significant causal strengths with respect to the indexes are identified as candidates for the cause of the fault. The proposed causal plot can identify correct fault causes even when the conventional contribution plots cannot identify them correctly.

In this study, we report the results of applying the proposed causal plot to a process benchmark problem—vinyl acetate monomer (VAM) manufacturing process [17,18]—which clearly shows that the causal plot appropriately diagnoses causes of faults that conventional contribution plots cannot diagnose. This advantage of the proposed method is important for realizing safe and stable operations in industrial processes.

A preliminary version of this work has been reported in [19]. In this study, we add a case study of the VAM process and a detailed analysis of the relationship between the causal plot and a recycle flow in processes.

2. Contribution Plot

In this section, conventional contribution plots based on MSPC are briefly explained.

It is assumed that we have a normal data matrix $\mathit{X}\in {\mathbb{R}}^{N\times P}$, where N and P are the number of samples and process variables. Before analysis, each variable is centered at zero mean and appropriately scaled. $\mathit{X}$ can be decomposed by means of singular value decomposition (SVD) as follows:

$$\begin{array}{cc}\hfill \mathit{X}& =\mathit{U}\mathbf{\Sigma }{\mathit{V}}^{\top }\hfill \\ \hfill & =\left[\begin{array}{cc}{\mathit{U}}_R& {\mathit{U}}_0\end{array}\right]\left[\begin{array}{cc}{\mathbf{\Sigma }}_R& \mathbf{0}\\ \mathbf{0}& {\mathbf{\Sigma }}_0\end{array}\right]{\left[\begin{array}{cc}{\mathit{V}}_R& {\mathit{V}}_0\end{array}\right]}^{\top }\hfill \end{array}$$

(1)

where $\mathit{U}\in {\mathbb{R}}^{N\times N}$ is the left singular matrix, $\mathbf{\Sigma }\in {\mathbb{R}}^{N\times P}$ is the diagonal matrix whose diagonal elements are singular values, $\mathit{V}\in {\mathbb{R}}^{P\times P}$ is the right singular matrix. SVD is identical to principal component analysis (PCA). In PCA, ${\mathit{V}}_R\in {\mathbb{R}}^{P\times R}$ is called the loading matrix, and $R(\le P)$ is the number of principal components. The column space of ${\mathit{V}}_R$ represents the subspace spanned by the principal components $\pi$. Thus, the dimensionality of $\mathit{X}$ is reduced from P to R.

The $T^2$ statistic of MSPC is defined as

$$\begin{array}{c}\hfill T^2={\mathit{x}}^{\top }{\mathit{V}}_R{\mathbf{\Sigma }}_R^{-2}{\mathit{V}}_R^{\top }\mathit{x}\end{array}$$

(2)

where $\mathit{x}$ is a newly measured sample. The $T^2$ statistic is the Mahalanobis distance between the origin and the projection of $\mathit{x}$ to $\pi$. The sample may be normal when the $T^2$ statistic is small.

The Q statistic is defined as follows:

$$\begin{array}{c}\hfill Q={\mathit{x}}^{\top }(\mathit{I}-{\mathit{V}}_R{\mathit{V}}_R^{\top })\mathit{x}.\end{array}$$

(3)

It is the squared distance between $\mathit{x}$ and $\pi$. That is, the Q statistic expresses the dissimilarity between the modeling data and $\mathit{x}$ from the viewpoint of the correlation among variables [20].

A fault is detected when either the $T^2$ or Q statistic exceeds a predefined control limit—$\overline{T^2}$ or $\overline{Q}$. The $\alpha$% confidence limits can be used for determining control limits. In MSPC, the number of principal components R should be appropriately tuned. It is possible to employ the Kaiser criterion, which states that principal components with eigenvalues greater than or equal to one can be used [21,22].

Although ordinal MSPC is based on the dimensionality reduction by PCA, various variations of MSPC have been proposed according to dimensionality reduction methods, such as kernel PCA (KPCA) [23], independent component analysis (ICA) [24], and canonical correlation analysis (CCA) [25]. However, PCA-based MSPC (PCA-MSPC) has still been widely used in industries [26] because of its ease of adaptability to real processes.

The Contribution plot expresses the contribution of each input variable to the $T^2$ and Q statistics [27]. The contribution of the mth variable $x_m$ is described as

$$\begin{array}{cc}\hfill C_m^{\left[T^2\right]}& ={\mathit{x}}^{\top }{\mathit{V}}_R{\mathbf{\Sigma }}_R^{-2}{x}_m{{\mathit{v}}_{\mathit{m}}}^{\top }\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill C_m^{\left[Q\right]}& ={(x_m-\widehat{x_m})}^2\hfill \end{array}$$

(5)

where ${\mathit{v}}_{\mathit{m}}$ denotes the mth row vector of ${\mathit{V}}_R$. When the contribution of the mth variable $C_m^{\left[T^2\right]}$ or $C_m^{\left[Q\right]}$ calculated in the fault condition is significantly larger than other variables, $x_m$ is diagnosed as a candidate for a cause of the fault.

3. Causal Plot

This study proposes a new fault diagnosis method based on causal analysis, referred to as a causal plot.

LiNGAM is a model expressing a causal structure among variables, designed to be used with data containing confounders [15,28]. An example of a causal structure is shown in Figure 1. The vertices represent variables. The directed edges express causal dependencies among the variables. In Figure 1, there is a directed edge from vertex $x_1$ to $x_2$, which means $x_1$ has a causal effect on $x_2$. LiNGAM assumes that the causal structure is a directed acyclic graph (DAG), which is a directed graph without a cycle, and that all variables are non-Gaussian.

In the LiNGAM model, each variable is generated as linear combinations of causal antecedent variables and an exogenous variable. The model in Figure 1 can be written as follows:

$$\begin{array}{cc}\hfill x_1& =e_1\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill x_2& =b_{12}{x}_1+e_2\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill x_3& =b_{13}{x}_1+b_{23}{x}_2+e_3\hfill \end{array}$$

(8)

$x_i$ and $e_i$ ($i=1,2,3$) are the observed and exogenous variables, and $b_{12}$, $b_{13}$, and $b_{23}$ are the coefficients expressing the causal strength.

In general, the LiNGAM model with p observed variables $x_i$ ($i=1,2,\dots ,p$) is expressed as a linear equation:

$$x_i=\sum _{j\ne i}{b}_{ji}{x}_j+e_i$$

(9)

where $b_{ij}$ are the coefficients. The variable vector $\mathit{x}\in {\mathbb{R}}^P$ is written as

$$\mathit{x}=\mathit{B}\mathit{x}+\mathit{e}$$

(10)

where $\mathit{e}\in {\mathbb{R}}^P$ is the exogenous variable vector, and $\mathit{B}\in {\mathbb{R}}^{P\times P}$ is the coefficient matrix of the LiNGAM model, which must be a lower triangular matrix whose diagonal components are zero due to the causal assumption. The goal of causal discovery with LiNGAM is to estimate the LiNGAM matrix $\mathit{B}$, which describes the causal relationships among the variables based on the assumptions of non-Gaussian process variables and acyclic causal relationships. Although there are several algorithms in LiNGAM, ICA-LiNGAM [15] and Direct-LiNGAM [29] have been widely used.

The causality among an arbitrary monitored index D of fault detection methods in addition to the process variables is estimated by means of LiNGAM. Process variables with significant causal strengths with respect to D are identified as candidates for the causes of the fault.

When a fault is detected between times s and $s+S$, the ith input vector of LiNGAM corresponding to the monitored index D is defined as follows:

$${\mathit{z}}_i=[x_{1,i},\dots ,x_{P,i},D_i]\in {\mathbb{R}}^{P+1}(i=s,\dots ,s+S).$$

(11)

In order to calculate causality with LiNGAM, more than $P+1$ samples are required since the number of samples must be bigger than that of variables. The input matrix of LiNGAM $\mathit{Z}$ is defined as

$$\mathit{Z}=\left[\begin{array}{c}{\mathit{z}}_s\\ {\mathit{z}}_{s+1}\\ ⋮\\ {\mathit{z}}_{s+S}\end{array}\right]\in {\mathbb{R}}^{S+1\times P+1}(S+1\ge P+1).$$

(12)

The LiNGAM coefficient matrix $\mathit{B}\in {\mathbb{R}}^{P+1\times P+1}$ is calculated by applying $\mathit{Z}$ to LiNGAM, whose $P+1$th column vector ${\mathit{b}}_{P+1}\in {\mathbb{R}}^{P+1}$ denotes the LiNGAM coefficient of the monitored index D corresponding to the process variables. Since the last element of ${\mathit{b}}_{P+1}$ is the causality of D to itself, it can be ignored.

The process variables whose LiNGAM coefficients in ${\mathit{b}}_{P+1}$ have significant absolute values are identified as candidates for the causes of the fault. The signs of ${\mathit{b}}_{P+1}$ indicate the causal effect directions (positive/negative) of the process variables on D. When MSPC is adopted as the fault detection method, D becomes the $T^2$ or Q statistics.

A procedure of causal plot calculation is summarized as follows:

• Generate the ith input vector ${\mathit{z}}_i=[x_{1,i},\dots ,x_{P,i},D_i]\in {\mathbb{R}}^{P+1}(i=s,\dots ,s+S)$ when a fault is detected between times s and $s+S$.
• Merge ${\mathit{z}}_i(i=s,\dots s+S)$ into one matrix: $\mathit{Z}={[{\mathit{z}}_s,{\mathit{z}}_{s+1},⋮,{\mathit{z}}_{s+S}]}^{\top }\in {\mathbb{R}}^{S+1\times P+1}(S+1\ge P+1)$.
• Apply $\mathit{Z}$ to LiNGAM and calculate the LiNGAM coefficient matrix $\mathit{B}\in {\mathbb{R}}^{P+1\times P+1}$.
• Extract the $P+1$th column vector ${\mathit{b}}_{P+1}\in {\mathbb{R}}^{P+1}$ of $\mathit{B}$ as the causal plot.

4. Case Study

The result of applying the proposed causal plot to the VAM manufacturing process is reported. The causal plots are compared with the conventional contribution plot by checking whether each method identifies correct fault causes or not. In this case study, PCA-MSPC is used for detecting faults and calculating the conventional contribution plot to test under a realistic situation since PCA-MSPC and the conventional contribution plot are currently used in many real processes [5,6,30].

4.1. VAM Process

The model of the VAM manufacturing process was developed by Luyben and Tyrus as a large production system containing standard chemical unit operations for real chemical components [17]. In this process, three raw materials, ethylene (${\mathrm{C}}_2{\mathrm{H}}_4$), oxygen (${\mathrm{O}}_2$), and acetate (HAc), are converted into a vinyl acetate (VAc) product. Water (${\mathrm{H}}_2\mathrm{O}$) and carbon dioxide (${\mathrm{CO}}_2$) are byproducts. Ethane (${\mathrm{C}}_2{\mathrm{H}}_6$) is an inert component that enters through a fresh ethylene feed stream. These three raw materials are mixed and introduced into a reactor, in which the following gas-phase reactions take place.

$$\begin{array}{c}{\mathrm{C}}_2{\mathrm{H}}_4+{\mathrm{CH}}_3\mathrm{COOH}+1/2{\mathrm{O}}_2⟶\\ {\mathrm{CH}}_2={\mathrm{CHOCOCH}}_3+{\mathrm{H}}_2\mathrm{O}\end{array}$$

(13)

$${\mathrm{C}}_2{\mathrm{H}}_4+3{\mathrm{O}}_2⟶2{\mathrm{CO}}_2+2{\mathrm{H}}_2\mathrm{O}$$

(14)

An overall process flow diagram of the VAM process is shown in Figure 2, in which the numbers indicate the stream number.

The reactor outlet gas with VAM is cooled by two coolers through stream 5. Unreacted AcOH, ${\mathrm{H}}_2\mathrm{O}$, and VAM are condensed into liquid VAM crude at the separator. The gas separated from the separator includes unreacted ${\mathrm{C}}_2{\mathrm{H}}_4$, ${\mathrm{O}}_2$, by-product ${\mathrm{CO}}_2$, inert ethane (${\mathrm{C}}_2{\mathrm{H}}_6$), and uncondensed VAM. This separated gas is compressed by the compressor into circulated recycle gas flow and then introduced into the absorber (stream 8). The uncondensed VAM is sent to the absorber via stream 6 and absorbed by cold AcOH, which is fed from the top of the absorber. The mixture of VAM and AcOH is discharged from the bottom of the absorber and mixed with the VAM crude in the intermediate buffer tank.

A part of VAM removed from the top of the absorber is recycled to the inlet of the process through stream 12, and the remaining part is introduced to the ${\mathrm{CO}}_2$ remover via stream 9. A part of the gas after the ${\mathrm{CO}}_2$ remover is purged (stream 11).

The VAM crude at the intermediate buffer tank is fed to an azeotropic distillation column through stream 13. The VAM-${\mathrm{H}}_2\mathrm{O}$ mixture discharged from the top of the column is condensed at the condenser and separated at the decanter. The VAM product is discharged as an organic product from the decanter. Unreacted AcOH is discharged from the bottom of the azeotropic distillation column and recycled to both the vaporizer and the absorber.

In this study, Visual Modeler (VM) (Omega Simulation Co., Ltd.) was used as a simulator of the VAM process [18]. There are 66 process variables in the VM model, which are indicated by circled numbers in Figure 2 and listed in

Table 1. Variables in VAM process.

No.	Variables	No.	Variables
1	stream 1 flow	34	column temperature
2	vaporizer steam flow	35	column temperature (control)
3	stream 3 flow	36	stream 14 temperature
4	separator outflow	37	stream 4 ${\mathrm{O}}_2$ molarity
5	stream 18 flow	38	stream 12 flow
6	absorber recycle flow	39	stream 2 flow
7	stream 9 flow	40	stream 19 flow
8	stream 11 flow	41	vaporizer outflow
9	stream 13 flow	42	heater steam flow
10	column steam flow	43	stream 4 flow
11	stream 17 flow	44	stream 5 flow
12	stream 15 flow	45	steam drum return flow
13	vaporizer level	46	steam drum inflow
14	steam drum level	47	separator gas outflow
15	separator level	48	stream 8 flow
16	absorber level	49	stream 7 flow
17	buffer tank level	50	stream 20 flow
18	column level	51	stream 10 flow
19	decanter sediment level	52	stream 16 flow
20	decanter non-sediment level	53	vaporizer steam pressure
21	vaporizer pressure	54	heater steam pressure
22	steam drum pressure	55	stream 6 pressure
23	separator outflow gas pressure	56	absober top pressure
24	column pressure	57	column top pressure
25	vaporizer outflow temperature	58	heater outflow temperature
26	heater temperature	59	reactor inflow steam temperature
27	reactor temperature	60	reactor inlet temperature
28	stream 5 temperature	61	absorber top temperature
29	temperature after heat exchange	62	stream 5 ${\mathrm{O}}_2$ molarity
30	separator inflow temperature	63	stream 13 flow (control)
31	absorber inflow temperature from separator	64	absorber bottom pressure
32	absorber recycle temperature	65	column bottom pressure
33	absorber inflow temperature from column	66	reactor outlet temperature

. The measurement duration of one dataset was 20 h with 7200 measurements, the sampling interval of the simulator being 10 s, which was defined as the default value of the simulator [18]. The normal and faulty data were defined as 7200 × 66 matrixes.

Faults in the VAM process, MAL1-MAL4, are provided by default in the VM model [18], which are described in

Table 2. Fault description in VAM process.

No.	Description	Type
1	${\mathrm{C}}_2{\mathrm{H}}_4$ feed composition	step
2	AcOH feed composition	step
3	${\mathrm{C}}_2{\mathrm{H}}_4$ feed pressure	ramp
4	${\mathrm{O}}_2$ feed pressure	ramp

. The “type” column in Table 2 indicates the type of the cause of fault, wherein “step” and “ramp” are step-like and ramp-like faults, respectively.

4.2. Fault Detection

Usually, a fault detection model is constructed using all variables measured in an objective process and variables are not selected for modeling because we cannot detect any fault if it occurs around variables that are not selected in the fault detection model. Thus, we used all 66 variables of the VAM process listed in Table 1 for fault detection.

An MSPC model was constructed with the normal operation data, and the number of retained principal components was determined as $R=15$ based on Kaiser [21]. The control limits of the $T^2$ and Q statistics were determined based on the 99% confidence limits.

Figure 3 shows the results of the fault detection with MSPC in MAL1–MAL4. In this figure, the top and bottom of each figure are the monitoring charts of the $T^2$ and Q statistics. The vertical line is the fault occurrence timing, and the horizontal dotted line indicates the control limit. It was confirmed that the $T^2$ and Q statistics exceeded their control limits shortly after the occurrences of faults in all cases. In addition, Supplementary Figure S1 illustrates the fault detection results for 20 h with MSPC in MAL1–MAL4. Thus, all faults were correctly detected with PCA-MSPC, which suggests that more complicated methods like kernel PCA-based MSPC are not needed in the VAM process.

4.3. Fault Diagnosis

The conventional contribution plots and the proposed causal plots of the $T^2$ and Q statistics were calculated. Samples within one hour after the occurrence of the fault were analyzed for the diagnosis of the cause of the fault, following Kanse et al., who reported that it might take about one hour to manually identify causes of faults [31]. Fault diagnosis methods based on the Granger causality were not adopted in this study because there were three or more variables in the VAM process. Direct-LiNGAM was used for causal plot calculation [29].

Figure 4 and Figure 5 illustrate the contributions of the top five variables and the absolute values of the top five LiNGAM coefficients, respectively.

The cause of fault MAL1 is the change in ${\mathrm{C}}_2{\mathrm{H}}_4$ feed composition, which strongly affects the operation of the reactor. According to the contribution plots, variables (27), (66), (28), and (62), which are related to the reactor and streams 4 and 5, had large contributions. The result of fault diagnosis using the contribution plots was correct.

According to the results of fault diagnosis using the causal plot, variables (27), (45), and (66) related to the reactor, and variables of stream (28), (37), and (62), were indicated as candidates for the causes of the fault. This result means that the result of fault diagnosis by means of the causal plot was also correct. Thus, both methods showed good results in the diagnosis.

MAL2 occurs when the AcOH feed changes, which directly affects the operation of the vaporizer. The contribution plots of the $T^2$ statistic indicated that variables (28) and (60) might be causes of the fault; however, they relate to reactor faults. On the other hand, the contribution plot of the Q statistic suggests that variables (32) and (61) might be the causes of the fault. They are variables of the absorber, which means that the result of the contribution plots is that neither the $T^2$ nor Q statistic was correct.

The proposed causal plot suggested that variables (1) and (21), which denote the vaporizer pressure and the stream 1 flow, controlled by the vaporizer pressure, might be causes of the fault. Since the vaporizer is affected by MAL2, the result of fault diagnosis by means of the causal plot was correct. The variable with the third largest absolute value in the LiNGAM coefficients of the $T^2$ statistic was variable (37) (the ${\mathrm{O}}_2$ molar concentration in stream 4), and that of the Q statistic was variable (13) (the vaporizer water level), which are also considered to be affected by MAL2. It is concluded that the contribution plots did not suggest correct causes of the fault. On the other hand, the proposed causal plots were able to identify the causes of the fault in MAL2.

MAL3 is caused due to changes in the ${\mathrm{C}}_2{\mathrm{H}}_4$ feed pressure, which influence streams 4 and 5 and the reactor. The contribution plots indicated that variables (28), (37), and (66), related to streams 4 and 5, and the reactor, were estimated as the causes of the fault. In the diagnosis results of the proposed causal plot, variables (28), (37), and (62) had strong causal effects on the $T^2$ statistic. On the other hand, variables (32) and (17), which are variables of the absorber and the buffer tank and are not related to MAL3, also had strong causal effects on the Q statistic. That is, the diagnosis result of the causal plot regarding only the $T^2$ statistic was correct. We discuss the reason why the causal plot of the Q statistic could not identify the cause of MAL3 in Section 4.4.

The cause of MAL4 is the pressure change of the ${\mathrm{O}}_2$ feed. This change affects the operation of streams 4 and 5, the heater, and the vaporizer. The contribution plot of the Q statistic estimated variables (37), (62), and (28) as causes of the fault. The contribution plot of the $T^2$ statistic indicated variable (9), which did not have causality with respect to the fault. On the other hand, in the proposed method, variables (1), (21), (42), and (54), which are variables of the vaporizer and the heater, were estimated as causes of the fault. Although the contribution plots did not correctly diagnose the cause of MAL4, the proposed causal plot suggested reasonable causes of the fault.

The results of fault diagnosis in the VAM process are summarized in

Table 3. Summary of fault diagnosis results in VAM process.

Method	Contribution Plot		Causal Plot
Statistic	${\mathit{T}}^{\mathbf{2}}$	$\mathit{Q}$	${\mathit{T}}^{\mathbf{2}}$	$\mathit{Q}$
MAL1	correct	correct	correct	correct
MAL2	incorrect	incorrect	correct	correct
MAL3	correct	correct	correct	incorrect
MAL4	incorrect	correct	correct	correct

. In all of MAL1–MAL4, the causal plots were able to appropriately indicate the causes of the faults. On the other hand, the contribution plots failed to correctly identify the causes of MAL2 and MAL4. Thus, the proposed causal plots are more suitable for diagnosing process faults than the conventional contribution plots.

4.4. Discussion

The proposed causal plot with the $T^2$ statistic correctly diagnosed causes in all of the faults in the case studies although the conventional contribution plot calculated from neither statistic could identify the cause of MAL2. In the causal plot, an incorrect diagnosis result was reached for MAL3 when using the LiNGAM coefficient of the Q statistic. Although the cause of MAL3 is the change in the ${\mathrm{C}}_2{\mathrm{H}}_4$ feed pressure, the proposed method identified variables (32), (17), and (63), which are not related to the feed pressure.

LiNGAM assumes that the causal relationship between variables is acyclic. According to Figure 5, variable (32) is located in a recycle stream. Because a recycle flow does not satisfy the acyclic assumption of LiNGAM, the proposed causal plot may not be able to estimate a correct causal inference; however, the results of fault diagnosis with the causal plot indicated appropriate causes of faults, except for MAL3, even with respect to a recycle flow.

In order to investigate the difference between MAL2, which was appropriately diagnosed, and MAL3, which was not correctly diagnosed by the proposed method, the cross-correlation between variables related to the causes of faults and the recycle flow in MAL2 and MAL3 was checked. Figure 6 shows the cross-correlation before and after the occurrence of faults. In this figure, the variables of the causes of the faults are variable (39) (stream 2 flow) in MAL2 and variable (1) (stream 1 flow) in MAL3, while variable (38) (stream 12 flow) is the recycle flow variable in both MAL2 and MAL3.

Before the occurrence of the MAL3 fault, the cross-correlation between variables (1) and (38) was close to zero. That is, there was no loop effect before the fault. However, the cross-correlation after the fault occurrence was more significant, which means that variables (1) and (38) are strongly correlated. In other words, the causality between these variables was cyclic in MAL3, which does not satisfy an assumption of LiNGAM.

On the other hand, the cross-correlation between (39) and (38) was close to zero before and after the fault occurrence in MAL2. Thus, the recycling flow did not cause a cyclic causality. In addition, it was confirmed that the cross-correlation did not change significantly before and after the fault occurrence in MAL1 and MAL4.

A recycle flow may cause a cyclic causality between process variables; however, there is also some delay in the propagation of the effect between them, and variables physically distant from each other do not have a correlation at that moment. Such situations would not affect the results of LiNGAM. Thus, MAL1, MAL2, and MAL4 satisfied such situations.

The foregoing indicates that whether there is a recycle flow should be checked by utilizing a process diagram before performing analysis with the proposed method because the results with LiNGAM may be impacted by a recycle flow. This is one of the limitations of the proposed method. Changes in the cross-correlation of variables around the recycle flow would be a useful tool to check whether the proposed causal plot can be applied to fault diagnosis.

The case studies included typical types of faults—step-like faults (MAL1 and MAL2) and ramp-like faults (MAL3 and MAL4). The results suggest that the proposed causal plots are efficacious even when the fault types are altered. In order to validate this, the fault patterns of MAL1 and MAL2 in the VAM process were switched from step-like faults to ramp-like faults. The ramp-like faults continued for three hours. In the same manner as the original step-like faults in MAL1 and MAL2, the ramp-like faults in MAL1 and MAL2 were detected appropriately by the $T^2$ and Q statistics with MSPC. Figure 7 and Figure 8 show the results of the fault diagnosis with the causal plot. Variables (66) and (28) were indicated as candidates for the cause of fault MAL1, and variables (1) and (21) for MAL2, which are the same results as those for the step-like faults. The proposed method can handle various types of faults in the same causes of faults. The proposed causal plot can be applied to a wide variety of faults regardless of their causes.

Although we validated the proposed method through application to the VAM process, we have also applied it to the Tennessee Eastman process, which is widely used as a process benchmark of fault detection and diagnosis methods [32], and showed its efficacy [19]. Therefore, it is concluded that the proposed method can be used for various processes.

5. Conclusions

A new fault diagnosis method, referred to as a causal plot, was proposed. The proposed causal plot was applied to the faulty data of the VAM manufacturing process, and the results showed that the proposed method correctly diagnosed the causes of faults with the $T^2$ statistic, even when they could not be diagnosed by the conventional contribution plots. In addition, we discussed the effect of the recycle flow in the process on the result of the causal plot from the viewpoint of cross-correlation.

The proposed causal plot can contribute to realizing a safe and efficient process operation because it can diagnose the causes of faults. We have applied the causal plot to real process data collected from a hot rolling process of a steel plant and confirmed its effectiveness.

In future works, the causal plot will be improved so that it can handle faults with cyclical causalities. An appropriate criterion of the LiNGAM coefficients derived by the causal plot will be investigated in order to identify which process variables may be the cause of the faults. Another problem is the application of the proposed data to big process data. As the expansion of LiNGAM on large datasets has been studied in [33], we will try to apply the proposed method to big processes utilizing [33].