Topology Optimization of Compliant Mechanisms Considering Manufacturing Uncertainty, Fatigue, and Static Failure Constraints
Abstract
:1. Introduction
2. Problem Formulation
2.1. Methods of the Manufacturability
2.2. Methods of the Objective Function
2.3. Methods of the Static Strength and Fatigue Failure
3. The Optimization Problem Statement
4. Sensitivity Analysis
4.1. Sensitivity of the Optimization Objective
4.2. Sensitivity of the Static Strength and Fatigue Failure
4.3. Sensitivity of the Volume
5. Numerical Implementation
6. Numerical Examples
6.1. Numerical Examples of the Inverter
6.2. Numerical Examples of the Gripper
7. Conclusions
- The von Mises stresses in the force inverter and compliant gripper were found to be approximately 120 MPa and 100 MPa, respectively. These stresses were below the material’s strength limit of 275 MPa.
- Compared with the previous topology optimization without fatigue constraints, the fatigue-constrained topology optimization can more effectively suppress the one-node hinge connection problems and avoid the phenomenon of stress concentration. Moreover, the maximum stress value of the compliant mechanism obtained using the fatigue-constrained topology optimization was lower, and the stress distribution was more uniform.
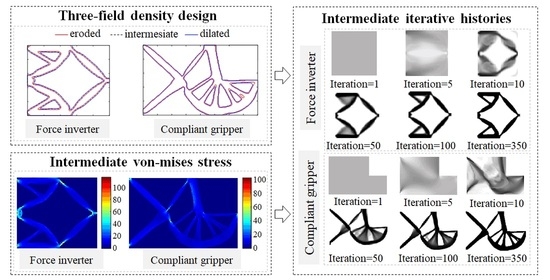
- The three-field density projection approach was successfully employed to control the minimum size in the layout optimization, thereby meeting the manufacturing process requirements. In addition, a gray level indicator, Mnd, was utilized to measure the gray level, and the maximum gray level of the real design was found to be less than 1.5%. The effectiveness of the proposed method was effectively demonstrated through two numerical examples.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Zhang, X. Optimal design of a planar parallel 3-dof nanopositioner with multi-objective. Mech. Mach. Theory 2017, 112, 61–83. [Google Scholar] [CrossRef]
- Alberola, J.A.M.; Fassi, I. Cyber-physical systems for micro-/nano-assembly operations: A survey. Curr. Robot. Rep. 2021, 2, 33–41. [Google Scholar] [CrossRef]
- Wang, X.; Meng, Y.; Huang, W.-W.; Li, L.; Zhu, Z.; Zhu, L. Design, modeling, and test of a normal-stressed electromagnetic actuated compliant nano-positioning stage. Mech. Syst. Signal Process. 2023, 185, 109753. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Zhou, R.; Zhu, Z.-H.; Kong, L.; Yang, X.; Zhu, L.; Zhu, Z. Development of a high-performance force sensing fast tool servo. IEEE Trans. Ind. Inform. 2021, 18, 35–45. [Google Scholar] [CrossRef]
- Zhao, D.; Zhu, Z.; Huang, P.; Guo, P.; Zhu, L.; Zhu, Z. Development of a piezoelectrically actuated dual-stage fast tool servo. Mech. Syst. Signal Process. 2020, 144, 106873. [Google Scholar] [CrossRef]
- Zhao, D.; Du, H.; Wang, H.; Zhu, Z. Development of a novel fast tool servo using topology optimization. Int. J. Mech. Sci. 2023, 250, 108283. [Google Scholar] [CrossRef]
- Sano, P.; Verotti, M.; Bosetti, P.; Belfiore, N.P. Kinematic synthesis of a d-drive mems device with rigid-body replacement method. J. Mech. Des. 2018, 140, 075001. [Google Scholar] [CrossRef]
- Yeon, A.; Yeo, H.G.; Roh, Y.; Kim, K.; Seo, H.-S.; Choi, H. A piezoelectric micro-electro-mechanical system vector sensor with a mushroom-shaped proof mass for a dipole beam pattern. Sens. Actuators A Phys. 2021, 332, 113129. [Google Scholar] [CrossRef]
- Salinić, S.; Nikolić, A. A new pseudo-rigid-body model approach for modeling the quasi-static response of planar flexure-hinge mechanisms. Mech. Mach. Theory 2018, 124, 150–161. [Google Scholar] [CrossRef]
- Kenton, B.J.; Leang, K.K. Design and control of a three-axis serial-kinematic high-bandwidth nanopositioner. IEEE/ASME Trans. Mechatron. 2011, 17, 356–369. [Google Scholar] [CrossRef]
- Ryu, J.W.; Lee, S.-Q.; Gweon, D.-G.; Moon, K.S. Inverse kinematic modeling of a coupled flexure hinge mechanism. Mechatronics 1999, 9, 657–674. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced mathematical modeling of the displacement amplification ratio for piezoelectric compliant mechanisms. Smart Mater. Struct. 2016, 25, 075022. [Google Scholar] [CrossRef]
- Li, C.; Chen, S.-C. Design of compliant mechanisms based on compliant building elements. Part I: Principles. Precis. Eng. 2023, 81, 207–220. [Google Scholar] [CrossRef]
- Chen, F.; Dong, W.; Yang, M.; Sun, L.; Du, Z. A pzt actuated 6-dof positioning system for space optics alignment. IEEE/ASME Trans. Mechatron. 2019, 24, 2827–2838. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Liu, Z.; Wang, R.; Zhu, L. Development of a piezoelectrically actuated two-degree-of-freedom fast tool servo with decoupled motions for micro-/nanomachining. Precis. Eng. 2014, 38, 809–820. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, Q.; Jin, M.; Zhang, X. Design of fully decoupled compliant mechanisms with multiple degrees of freedom using topology optimization. Mech. Mach. Theory 2018, 126, 413–428. [Google Scholar] [CrossRef]
- Lum, G.Z.; Teo, T.J.; Yeo, S.H.; Yang, G.; Sitti, M. Structural optimization for flexure-based parallel mechanisms-towards achieving optimal dynamic and stiffness properties. Precis. Eng. 2015, 42, 195–207. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X. A new topology optimization method for planar compliant parallel mechanisms. Mech. Mach. Theory 2016, 95, 42–58. [Google Scholar] [CrossRef]
- Pinskier, J.; Shirinzadeh, B.; Ghafarian, M.; Das, T.K.; Al-Jodah, A.; Nowell, R. Topology optimization of stiffness constrained flexure-hinges for precision and range maximization. Mech. Mach. Theory 2020, 150, 103874. [Google Scholar] [CrossRef]
- Pham, M.T.; Yeo, S.H.; Teo, T.J.; Wang, P.; Nai, M.L.S. A decoupled 6-dof compliant parallel mechanism with optimized dynamic characteristics using cellular structure. Machines 2021, 9, 5. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of compliant mechanisms using continuum topology optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Liu, M.; Zhan, J.; Zhu, B.; Zhang, X. Topology optimization of flexure hinges with a prescribed compliance matrix based on the adaptive spring model and stress constraint. Precis. Eng. 2021, 72, 397–408. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chen, Y.; Yang, S.-Y. Topology optimization and prototype of a multimaterial-like compliant finger by varying the infill density in 3d printing. Soft Robot. 2022, 9, 837–849. [Google Scholar] [CrossRef] [PubMed]
- Dorn, W.S. Automatic design of optimal structures. J. Mec. 1964, 3, 25–52. [Google Scholar]
- Nishiwaki, S.; Frecker, M.I.; Min, S.; Kikuchi, N. Topology optimization of compliant mechanisms using the homogenization method. Int. J. Numer. Methods Eng. 1998, 42, 535–559. [Google Scholar] [CrossRef]
- Takezawa, A.; Nishiwaki, S.; Kitamura, M. Shape and topology optimization based on the phase field method and sensitivity analysis. J. Comput. Phys. 2010, 229, 2697–2718. [Google Scholar] [CrossRef]
- Wang, N.F.; Zhang, X.M. Topology optimization of compliant mechanisms using pairs of curves. Eng. Optim. 2015, 47, 1497–1522. [Google Scholar] [CrossRef]
- Ansola, R.; Veguería, E.; Canales, J.; T’arrago, J.A. A simple evolutionary topology optimization procedure for compliant mechanism design. Finite Elem. Anal. Des. 2007, 44, 53–62. [Google Scholar] [CrossRef]
- Luo, Z.; Tong, L.; Wang, M.Y.; Wang, S. Shape and topology optimization of compliant mechanisms using a parameterization level set method. J. Comput. Phys. 2007, 227, 680–705. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X.; Zhu, B. Imposing minimum length scale in moving morphable component (mmc)-based topology optimization using an effective connection status (ecs) control method. Comput. Methods Appl. Mech. Eng. 2019, 351, 667–693. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, L.; Yang, J.; Zhang, Y.; Abdel-Malek, K. Compliant mechanism design using multi-objective topology optimization scheme of continuum structures. Struct. Multidiscip. Optim. 2005, 30, 142–154. [Google Scholar] [CrossRef]
- Duysinx, P.; Bendsøe, M.P. Topology optimization of continuum structures with local stress constraints. Int. J. Numer. Methods Eng. 1998, 43, 1453–1478. [Google Scholar] [CrossRef]
- de Troya, M.A.S.; Tortorelli, D.A. Adaptive mesh refinement in stress-constrained topology optimization. Struct. Multidiscip. Optim. 2018, 58, 2369–2386. [Google Scholar] [CrossRef]
- Chu, S.; Gao, L.; Xiao, M.; Luo, Z.; Li, H. Stress-based multi-material topology optimization of compliant mechanisms. Int. J. Numer. Methods Eng. 2018, 113, 1021–1044. [Google Scholar] [CrossRef]
- de Assis Pereira, A.; Cardoso, E.L. On the influence of local and global stress constraint and filtering radius on the design of hinge-free compliant mechanisms. Struct. Multidiscip. Optim. 2018, 58, 641–655. [Google Scholar] [CrossRef]
- Conlan-Smith, C.; James, K.A. A stress-based topology optimization method for heterogeneous structures. Struct. Multidiscip. Optim. 2019, 60, 167–183. [Google Scholar] [CrossRef]
- Deng, H.; Vulimiri, P.S.; To, A.C. An efficient 146-line 3d sensitivity analysis code of stress-based topology optimization written in matlab. Optim. Eng. 2021, 23, 1733–1757. [Google Scholar] [CrossRef]
- Roin, T.; Montemurro, M.; Pailh, J. Stress-based topology optimization through non-uniform rational basis spline hyper-surfaces. Mech. Adv. Mater. Struct. 2022, 29, 3387–3407. [Google Scholar] [CrossRef]
- Bruggi, M. On an alternative approach to stress constraints relaxation in topology optimization. Struct. Multidiscip. Optim. 2008, 36, 125–141. [Google Scholar] [CrossRef]
- Le, C.; Norato, J.; Bruns, T.; Ha, C.; Tortorelli, D. Stress-based topology optimization for continua. Struct. Multidiscip. Optim. 2010, 41, 605–620. [Google Scholar] [CrossRef]
- Jeong, S.H.; Choi, D.-H.; Yoon, G.H. Fatigue and static failure considerations using a topology optimization method. Appl. Math. Model. 2015, 39, 1137–1162. [Google Scholar] [CrossRef]
- Nabaki, K.; Shen, J.; Huang, X. Evolutionary topology optimization of continuum structures considering fatigue failure. Mater. Des. 2019, 166, 107586. [Google Scholar] [CrossRef]
- Holmberg, E.; Torstenfelt, B.; Klarbring, A. Fatigue constrained topology optimization. Struct. Multidiscip. Optim. 2014, 50, 207–219. [Google Scholar] [CrossRef]
- Collet, M.; Bruggi, M.; Duysinx, P. Topology optimization for minimum weight with compliance and simplified nominalstress constraints for fatigue resistance. Struct. Multidiscip. Optim. 2017, 55, 839–855. [Google Scholar] [CrossRef]
- Oest, J.; Lund, E. Topology optimization with finite-life fatigue constraints. Struct. Multidiscip. Optim. 2017, 56, 1045–1059. [Google Scholar] [CrossRef]
- Chen, Z.; Long, K.; Wen, P.; Nouman, S. Fatigue-resistance topology optimization of continuum structure by penalizing the cumulative fatigue damage. Adv. Eng. Softw. 2020, 150, 102924. [Google Scholar] [CrossRef]
- Sigmund, O. Manufacturing tolerant topology optimization. Acta Mech. Sin. 2009, 25, 227–239. [Google Scholar] [CrossRef]
- Wang, F.; Jensen, J.S.; Sigmund, O. Robust topology optimization of photonic crystal waveguides with tailored dispersion properties. JOSA B 2011, 28, 387–397. [Google Scholar] [CrossRef]
- Schevenels, M.; Lazarov, B.S.; Sigmund, O. Robust topology optimization accounting for spatially varying manufacturing errors. Comput. Methods Appl. Mech. Eng. 2011, 200, 3613–3627. [Google Scholar] [CrossRef]
- Lazarov, B.S.; Schevenels, M.; Sigmund, O. Robust design of large-displacement compliant mechanisms. Mech. Sci. 2011, 2, 175–182. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhang, L. Robust structural topology optimization considering boundary uncertainties. Comput. Methods Appl. Mech. Eng. 2013, 253, 356–368. [Google Scholar] [CrossRef]
- Zhang, W.; Kang, Z. Robust shape and topology optimization considering geometric uncertainties with stochastic level set perturbation. Int. J. Numer. Methods Eng. 2017, 110, 31–56. [Google Scholar] [CrossRef]
- da Silva, G.A.; Beck, A.T.; Sigmund, O. Topology optimization of compliant mechanisms with stress constraints and manufacturing error robustness. Comput. Methods Appl. Mech. Eng. 2019, 354, 397–421. [Google Scholar] [CrossRef]
- da Silva, G.A.; Beck, A.T.; Sigmund, O. Topology optimization of compliant mechanisms considering stress constraints, manufacturing uncertainty and geometric nonlinearity. Comput. Methods Appl. Mech. Eng. 2020, 365, 112972. [Google Scholar] [CrossRef]
- Liu, M.; Zhan, J.; Zhu, B.; Zhang, X. Topology optimization of compliant mechanism considering actual output displacement using adaptive output spring stiffness. Mech. Mach. Theory 2020, 146, 103728. [Google Scholar] [CrossRef]
- Svanberg, K. Mma and Gcmma-Two Methods for Nonlinear Optimization; KTH: Stockholm, Sweden, 2007; Volume 1, pp. 1–15. [Google Scholar]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Qian, X.; Sigmund, O. Topological design of electromechanical actuators with robustness toward over-and under-etching. Comput. Methods Appl. Mech. Eng. 2013, 253, 237–251. [Google Scholar] [CrossRef]














| Parameter | Symbol | Value | Parameter | Symbol | Value |
|---|---|---|---|---|---|
| Elastic modulus for solid element | Fatigue limit of the elements | ||||
| Elastic modulus for void element | MPa | Yielding stress | MPa | ||
| Poisson’s ratio | Ultimate stress | MPa | |||
| Penalty parameter | Fatigue strength coefficient | MPa | |||
| Material density | Fatigue strength exponents | −0.1326 | |||
| Volume fraction | 0.3 | Allowable life cycles | |||
| Stress relaxation coefficient | Filter radius | ||||
| Initial scaling coefficient | Small positive value | ||||
| P-norm aggregation parameter | Maximum force | N | |||
| Control parameter | Minimum force | N |
| Parameter | Symbol | Eroded | Intermediate | Dilated |
|---|---|---|---|---|
| Output displacement | 99.8876 | 99.8850 | 99.8909 | |
| Amplification ratio | 0.69 | 0.733 | 0.727 | |
| Volume fraction | 0.252 | 0.302 | 0.346 | |
| Fatigue failure 1 | 0.84 | 0.89 | 1.26 | |
| Fatigue failure 2 | 0.678 | 0.75 | 0.865 | |
| Static failure 1 | 0.378 | 0.418 | 0.482 | |
| Static failure 2 | 0.378 | 0.418 | 0.482 | |
| Gray level indicator | 2.5% | 1.5% | 1.8% |
| Parameter | Symbol | Eroded | Intermediate | Dilated |
|---|---|---|---|---|
| Output displacement | 99.9698 | 99.9665 | 99.9657 | |
| Amplification ratio | 0.204 | 0.231 | 0.238 | |
| Volume fraction | 0.266 | 0.307 | 0.327 | |
| Fatigue failure 1 | 0.697 | 0.786 | 0.817 | |
| Fatigue failure 2 | 0.587 | 0.663 | 0.689 | |
| Static failure 1 | 0.327 | 0.370 | 0.384 | |
| Static failure 2 | 0.327 | 0.370 | 0.384 | |
| Gray level indicator | 2.8% | 0.9% | 1.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Wang, H. Topology Optimization of Compliant Mechanisms Considering Manufacturing Uncertainty, Fatigue, and Static Failure Constraints. Processes 2023, 11, 2914. https://doi.org/10.3390/pr11102914
Zhao D, Wang H. Topology Optimization of Compliant Mechanisms Considering Manufacturing Uncertainty, Fatigue, and Static Failure Constraints. Processes. 2023; 11(10):2914. https://doi.org/10.3390/pr11102914
Chicago/Turabian StyleZhao, Dongpo, and Haitao Wang. 2023. "Topology Optimization of Compliant Mechanisms Considering Manufacturing Uncertainty, Fatigue, and Static Failure Constraints" Processes 11, no. 10: 2914. https://doi.org/10.3390/pr11102914
APA StyleZhao, D., & Wang, H. (2023). Topology Optimization of Compliant Mechanisms Considering Manufacturing Uncertainty, Fatigue, and Static Failure Constraints. Processes, 11(10), 2914. https://doi.org/10.3390/pr11102914