Surface Topography Model of Ultra-High Strength Steel AF1410 Based on Dynamic Characteristics of Milling System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Characteristics
2.2. Methods
2.2.1. Surface Roughness Characterization Parameters
2.2.2. Experimental Equipment and Conditions
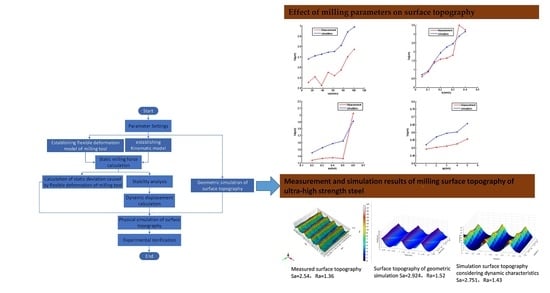
3. Results
3.1. Milling Surface Topography Model
3.1.1. Formation of Milling Surface Topography
3.1.2. Milling Tool Flexible Deformation Model
3.1.3. Tool-Workpiece Dynamic Displacement Based on Regenerative Flutter Model
3.1.4. Milling Surface Topography Model
3.2. Simulation of Surface Topography Based on Dynamic Characteristics of Milling System
3.2.1. Simulation Model
Ultra-High Strength Steel Workpiece Model
Milling Tool Micro Element Setting
3.2.2. Simulation Program Flow
Parameter Setting
- Cutting parameter setting
- 2.
- Tool parameter setting
- 3.
- Time step setting
Stability Analysis
Static Milling Force Calculation
Tool and Workpiece Dynamic Displacement Calculation
Geometric Simulation of Surface Topography
Physical Simulation of Surface Topography
3.3. Experimental Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Araki, T. Ultrahigh-strength Steels. J. Tetsu-Hagane 2010, 52, 163–186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kernen, L.; Kangaspuoskari, M.; Niskanen, J. Ultrahigh-strength steels at elevated temperatures. J. Constr. Steel Res. 2021, 183, 106739. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, C. Recent progress of chatter prediction, detection and suppression in milling. Mech. Syst. Signal Process. 2020, 143, 106840. [Google Scholar] [CrossRef]
- Artetxe, E.; Olvera, D.; de Lacalle, L.N.L.; Campa, F.J.; Olvera, D.; Lamikiz, A. Solid subtraction model for the surface topography prediction in flank milling of thin-walled integral blade rotors (IBRs). Int. J. Adv. Manuf. Technol. 2017, 90, 741–752. [Google Scholar] [CrossRef]
- Sun, Y.; Jia, J.; Xu, J.; Chen, M.; Niu, J. Path, feedrate and trajectory planning for free-from surface machining: A state-of-the-art review. Chin. J. Aeronaut. 2022, 35, 12–29. [Google Scholar] [CrossRef]
- Du, S.; Xi, L. High Definition Metrology Based Surface Quality Control and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kartal, F.; Yerlikaya, Z.; Gkkaya, H. Effects of machining parameters on surface roughness and macro surface characteristics when the machining of Al-6082 T6 alloy using AWJT. Measurement 2017, 95, 216–222. [Google Scholar] [CrossRef]
- Durakbasa, M.N.; Akdogan, A.; Vanli, A.S.; Bulutsuz, A.G. Optimization of end milling parameters and determination of the effects of edge profile for high surface quality of AISI H13 steel by using precise and fast measurements. Measurement 2015, 68, 92–99. [Google Scholar] [CrossRef]
- Liu, G.; Zou, B.; Huang, C.; Wang, X.; Liu, Z. Tool damage and its effect on the machined surface roughness in high-speed face milling the 17-4PH stainless steel. Int. J. Adv. Manuf. Technol. 2016, 83, 257–264. [Google Scholar] [CrossRef]
- Banerjee, N.; Sharma, A. Multi-Point Injection Minimum Quantity Lubrication Machining. Mater. Sci. Forum. 2015, 830–831, 108–111. [Google Scholar] [CrossRef]
- Jersák, J.; Simon, S. Influence of Cooling Lubricants on the Surface Roughness and Energy Efficiency of the Cutting Machine Tools. Int. J. Appl. Mech. 2017, 22, 779–787. [Google Scholar] [CrossRef] [Green Version]
- Alagarsamy, S.V.; Ravichandran, M.; Meignanamoorthy, M.; Sakthivelu, S.; Dineshkumar, S. Prediction of surface roughness and tool wear in milling process on brass (C26130) alloy by Taguchi technique. Mater. Today Proc. 2020, 21, 189–193. [Google Scholar] [CrossRef]
- Li, S.; Li, S.; Liu, Z.; Vladimirovich, P.A. Roughness prediction model of milling noise-vibration-surface texture multi-dimensional feature fusion for N6 nickel metal. J. Manuf. Process. 2022, 79, 166–176. [Google Scholar] [CrossRef]
- Arizmendi, M.; Jiménez, A. Modelling and analysis of surface topography generated in face milling operations. Int. J. Mech. Sci. 2019, 163, 105061. [Google Scholar] [CrossRef]
- Urbikain, G.; Trejo, D.O.; Luo, M.; Lacalle, L.; Elías-Zuiga, A. Surface roughness prediction with new barrel-shape mills considering runout: Modelling and validation. Measurement 2021, 173, 108670. [Google Scholar] [CrossRef]
- Wang, L.; Ge, S.; Si, H.; Yuan, X.; Duan, F. Roughness control method for five-axis flank milling based on the analysis of surface topography. Int. J. Mech. Sci. 2020, 169, 105337. [Google Scholar] [CrossRef]
- Kumar, H.; Ramkumar, J.; Venkatesh, K.S. Surface texture evaluation using 3D reconstruction from images by parametric anisotropic BRDF. Measurement 2018, 125, 612–633. [Google Scholar] [CrossRef]
- Too, M.X.; Ratnam, M.M.; Akil, H.M. Investigation on the effect of machining parameters on surface roughness during turning of kenaf fiber-reinforced composite using non-contact vision method. Int. J. Adv. Manuf. Technol. 2020, 110, 309–325. [Google Scholar] [CrossRef]
- Nouhi, S.; Pour, M. Prediction of surface roughness of various machining processes by a hybrid algorithm including time series analysis, wavelet transform and Multi View Embedding. Measurement 2021, 184, 109904. [Google Scholar] [CrossRef]
- Urbikain, G.; Lacalle, L.D. Modelling of surface roughness in inclined milling operations with circle-segment end mills. Simul. Model. Pract. Theory 2018, 84, 161–176. [Google Scholar] [CrossRef]
- Arizmendi, M.; Campa, F.J.; Fernández, J.; Lacalle, L.; Gil, A.; Bilbao, E. Model for surface topography prediction in peripheral milling considering tool vibration. CIRP Ann.-Manuf. Technol. 2009, 58, 93–96. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, Z.; Guo, Q.; Xu, J. A novel method to predict surface topography in robotic milling of directional plexiglas considering cutter dynamical displacement. J. Mater. Process. Technol. 2022, 304, 117545. [Google Scholar] [CrossRef]
- Lu, X.; Hu, X.; Jia, Z.; Liu, M.; Liang, S.Y. Model for the prediction of 3D surface topography and surface roughness in micro-milling Inconel 718. Int. J. Adv. Manuf. Technol. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Zhuo, Y.; Han, Z.; An, D.; Jin, H. Surface topography prediction in peripheral milling of thin-walled parts considering cutting vibration and material removal effect. Int. J. Mech. Sci. 2021, 211, 106797. [Google Scholar] [CrossRef]
- Chen, Q.H. Modelling and simulation of surface topography machined by peripheral milling considering tool radial runout and axial drift. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2227–2240. [Google Scholar] [CrossRef]
- Chen, W.; Xie, W.; Huo, D.; Kai, Y. A novel 3D surface generation model for micro milling based on homogeneous matrix transformation and dynamic regenerative effect. Int. J. Mech. Sci. 2018, 144, 146–157. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Du, S.; Wang, B.; Lv, J.; Deng, Y. High Definition Metrology-Based Quality Improvement of Surface Texture in Face Milling of Workpieces with Discontinuous Surfaces. J. Manuf. Sci. 2022, 144, 031001. [Google Scholar] [CrossRef]
- Xu, J.; Yan, F.; Li, Y.; Yang, Z.; Li, L. Multiobjective optimization of milling parameters for ultrahigh-strength steel af1410 based on the nsga-ii method. Adv. Mater. Sci. Eng. 2020, 2020, 8796738. [Google Scholar] [CrossRef]
- Podulka, P. Selection of Methods of Surface Texture Characterisation for Reduction of the Frequency-Based Errors in the Measurement and Data Analysis Processes. Sensors 2022, 22, 791. [Google Scholar] [CrossRef]
- Giusca, C.L.; Claverley, J.D.; Sun, W.; Leach, R.K.; Helmli, F.; Chavigner, M. Practical estimation of measurement noise and flatness deviation on focus variation microscopes. CIRP. Ann.-Manuf. Technol. 2014, 63, 545–548. [Google Scholar] [CrossRef]
- Zhao, C.; Lv, J.; Du, S. Geometrical deviation modeling and monitoring of 3D surface based on multi-output Gaussian process. Measurement 2022, 199, 111569. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Response Sensitivity Analysis of the Dynamic Milling Process Based on the Numerical Integration Method. Chin. J. Mech. Eng. 2012, 25, 940–946. [Google Scholar] [CrossRef]
- Yu, L. Prediction of chatter considering the effect of axial cutting depth on cutting force coefficients in end milling. Int. J. Adv. Manuf. Technol. 2018, 96, 3345–3354. [Google Scholar] [CrossRef]

















| Element | C | Co | Ni | Cr | Mo | Si | Mn | P | S |
|---|---|---|---|---|---|---|---|---|---|
| wt.% | 0.16 | 13.83 | 9.93 | 1.95 | 1.04 | 0.01 | 0.02 | 0.006 | 0.001 |
| Tensile Strength | Yield Strength | Elongation Rate | Surface Shrinkage |
|---|---|---|---|
| 1620 MPa | 1480 MPa | 12% | 60% |
| Mode | Natural Frequency (Hz) | Damping Ratio (%) |
|---|---|---|
| 1 | 197.334 | 5.65 |
| 2 | 281.122 | 3.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Yan, F.; Wan, X.; Li, Y.; Zhu, Q. Surface Topography Model of Ultra-High Strength Steel AF1410 Based on Dynamic Characteristics of Milling System. Processes 2023, 11, 641. https://doi.org/10.3390/pr11020641
Xu J, Yan F, Wan X, Li Y, Zhu Q. Surface Topography Model of Ultra-High Strength Steel AF1410 Based on Dynamic Characteristics of Milling System. Processes. 2023; 11(2):641. https://doi.org/10.3390/pr11020641
Chicago/Turabian StyleXu, Jin, Fuwu Yan, Xiaojin Wan, Yan Li, and Qiang Zhu. 2023. "Surface Topography Model of Ultra-High Strength Steel AF1410 Based on Dynamic Characteristics of Milling System" Processes 11, no. 2: 641. https://doi.org/10.3390/pr11020641
APA StyleXu, J., Yan, F., Wan, X., Li, Y., & Zhu, Q. (2023). Surface Topography Model of Ultra-High Strength Steel AF1410 Based on Dynamic Characteristics of Milling System. Processes, 11(2), 641. https://doi.org/10.3390/pr11020641