Study on Verification Approach and Multicontact Points Issue When Modeling Cyperus esculentus Seeds Based on DEM
Abstract
:1. Introduction
2. Cyperus Esculentus Seed Modeling
3. Model Verification
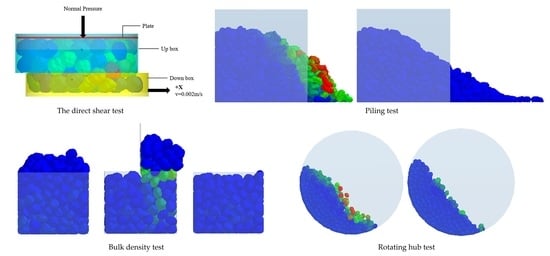
3.1. Physical Tests
3.1.1. The Direct Shear Test
3.1.2. Piling Test
3.1.3. Bulk Density Test
3.1.4. Rotating Hub Test
3.2. Simulation Analysis
3.2.1. Direct Shear Test Simulation
3.2.2. Piling Test Simulation
3.2.3. Bulk Density Test Simulation
3.2.4. Rotating Hub Test Simulation
4. Multicontact Points Issue
4.1. Influence of Multicontact Points on Particle Assembly Movement
4.2. Influence of Multicontact Points on Individual Particle Movement
4.3. Influence of Young’s Modulus on Multiple Contact Points
5. Conclusions
- (1)
- The direct shear test, piling test, bulk density test, and rotating hub test were used to verify the created DEM models with different numbers of filing spheres. Through comparisons between the experimental results and the simulated results, combined with CPU computational time, the DEM modeling created in this paper could achieve better simulation accuracies with fewer filing spheres. According to the simulation results, the 9-sphere model with Jinong 1, the 11-sphere model with Jinong 2, and the 9-sphere model with Jinong 3 could provide a good compromise between simulation accuracy and time consumed.
- (2)
- According to the simulation results, some limitations were present when using one single verification test, and the differences in DEM models with different numbers of filing spheres could not be fully described. Therefore, to improve the reliability of the verification approach and guarantee the accuracy of the model, more varieties of tests are required. In addition, the precision particle shape model could not markedly improve the simulation accuracy. In contrast, the greater the number of filing spheres included, the longer the CPU calculation time consumed.
- (3)
- Comparing the HMNR model with the HM model, the influence of the multicontact points on the movement behavior of the particle assembly model and individual particle model based on the MS method was studied through simulation analysis of the rotating hub test and the free drop test. According to the simulation results, the multicontact points affected the motion behavior of individual particles. In contrast, the influence of multiple contact points on the movement behavior of particle assembly was insignificant.
- (4)
- In addition, the relationships between the moisture content of seeds and Young’s modulus, Young’s modulus, and the number of contact points were also studied in simulations and experiments; with an increasing Young’s modulus, the number of contact points decreased, while the rebound height increased when creating the particle model based on the MS method. According to the experimental results, with increasing moisture content, Young’s modulus decreased, while the tri-axial dimensions increased.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heidarian, A.; Cheung, S.C.P.; Rosengarten, G. The effect of flow rate and concentration on the electrical conductivity of slurry electrodes using a coupled computational fluid dynamic and discrete element method (CFD–DEM) model. Electrochem. Commun. 2021, 126, 107017. [Google Scholar] [CrossRef]
- Schrader, M.; Pommerehne, K.; Wolf, S.; Finke, B.; Schilde, C.; Kampen, I.; Lichtenegger, T.; Krull, R.; Kwade, A. Design of a CFD-DEM-based method for mechanical stress calculation and its application to glass bead-enhanced cultivations of filamentous Lentzea aerocolonigenes. Biochem. Eng. J. 2019, 148, 116–130. [Google Scholar] [CrossRef]
- Parizi, E.; Khojeh, S.; Hosseini, S.M.; Moghadam, Y.J. Application of Unmanned Aerial Vehicle DEM in flood modeling and comparison with global DEMs: Case study of Atrak River Basin, Iran. J. Environ. Manag. 2022, 317, 115492. [Google Scholar] [CrossRef] [PubMed]
- Harnby, N.; Nienow, A.W.; Edwards, M.F. Mixing in the Process Industries: Second Edition. Powder Technol. 1993, 75, 104–105. [Google Scholar]
- Laurent, B.F.C.; Cleary, P.W. Comparative study by PEPT and DEM for flow and mixing in a ploughshare mixer. Powder Technol. 2012, 228, 171–186. [Google Scholar] [CrossRef]
- Najafi-Sani, M.A.; Mansourpour, Z. A new GPU-based DEM simulator for polydispersed granular systems with wide size distribution and its application in the silo discharge. Adv. Powder Technol. 2022, 33, 103704. [Google Scholar] [CrossRef]
- Ibrahim, A.; Meguid, M.A. CFD-DEM modeling of geotextile clogging in tunnel drainage systems. Geotext. Geomembr. 2022, 50, 932–945. [Google Scholar] [CrossRef]
- Niu, H.; Yang, D.-L.; Sun, Q.; Pu, Y.; Gao, T.; Wang, J.-X. A new method for predicting the maximum filler loading of dental resin composites based on DEM simulations and experiments. Dent. Mater. 2020, 36, e375–e385. [Google Scholar] [CrossRef]
- Langston, P.A.; Al-Awamleh, M.A.; Fraige, F.Y.; Asmar, B.N. Distinct element modelling of non-spherical frictionless particle flow. Chem. Eng. Sci. 2004, 59, 425–435. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Force model considerations for glued-sphere discrete element method simulation. Chem. Eng. Sci. 2009, 64, 3466–3475. [Google Scholar] [CrossRef]
- Lu, G.; Third, J.R.; Müller, C.R. Critical assessment of two approaches for evaluating contacts between super-quadric shaped particles in DEM simulations. Chem. Eng. Sci. 2012, 78, 226–235. [Google Scholar] [CrossRef]
- Dong, K.; Wang, C.; Yu, A. A novel method based on orientation discretization for discrete element modeling of non-spherical particles. Chem. Eng. Sci. 2015, 126, 500–516. [Google Scholar] [CrossRef]
- Lin, X.; Ng, T.-T. Contact detection algorithms for three-dimensional ellipsoids in discrete element modelling. Int. J. Numer. Anal. Methods Geomech. 1996, 33, A113–A114. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.A.; Zhao, D.; Ghaboussi, J. A fast contact detection algorithm for 3-D discrete element method. Comput. Geotech. 2004, 31, 575–587. [Google Scholar] [CrossRef]
- Xu, T.; Yu, J.; Yu, Y.; Wang, Y. A modelling and verification approach for soybean seed particles using the discrete element method. Adv. Powder Technol. 2018, 29, 3274–3290. [Google Scholar] [CrossRef]
- Yan, D.; Yu, J.; Wang, Y.; Zhou, L.; Yu, Y. A general modelling method for soybean seeds based on the discrete element method. Powder Technol. 2020, 372, 212–226. [Google Scholar] [CrossRef]
- Wang, X.; Yu, J.; Lv, F.; Wang, Y.; Fu, H. A multi-sphere based modelling method for maize grain assemblies. Adv. Powder Technol. 2017, 28, 584–595. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, J.; Xue, D.; Wang, Y.; Zhang, Q.; Ren, L. An approach to and validation of maize-seed-assembly modelling based on the discrete element method. Powder Technol. 2018, 328, 167–183. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, J.; Liang, L.; Yu, Y.; Yan, D.; Sun, K.; Wang, Y. Study on key issues in the modelling of maize seeds based on the multi-sphere method. Powder Technol. 2021, 394, 791–812. [Google Scholar] [CrossRef]
- Sun, K.; Yu, J.; Liang, L.; Wang, Y.; Yan, D.; Zhou, L.; Yu, Y. A DEM-based general modelling method and experimental verification for wheat seeds. Powder Technol. 2022, 401, 117353. [Google Scholar] [CrossRef]
- Pasha, M.; Hare, C.; Ghadiri, M.; Gunadi, A.; Piccione, P.M. Effect of particle shape on flow in discrete element method simulation of a rotary batch seed coate. Powder Technol. 2016, 296, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Zhang, R.; Zhu, F.; Feng, W.; Wang, Y.; Wang, J. A DEM-Based Modeling Method and Simulation Parameter Selection for Cyperus esculentus Seeds. Processes 2022, 10, 1729. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Rickelt, S.; Wirtz, S.; Scherer, V. A study on the validity of the multi-sphere Discrete Element Method. Powder Technol. 2008, 188, 153–165. [Google Scholar] [CrossRef]
- Höhner, D.; Wirtz, S.; Kruggel-Emden, H.; Scherer, V. Comparison of the multi-sphere and polyhedral approach to simulate non-spherical particles within the discrete element method: Influence on temporal force evolution for multiple contacts. Powder Technol. 2011, 208, 643–656. [Google Scholar] [CrossRef]
- Yan, D.; Yu, J.; Liang, L.; Wang, Y.; Yu, Y.; Zhou, L.; Sun, K.; Liang, P. A Comparative Study on the Modelling of Soybean Particles Based on the Discrete Element Method. Processes 2021, 9, 286. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, J.; Wang, Y.; Yan, D.; Yu, Y. A study on the modelling method of maize-seed particles based on the discrete element method. Powder Technol. 2020, 374, 353–376. [Google Scholar] [CrossRef]
- Yardeny, I.; Portnikov, D.; Kalman, H. Experimental investigation of the coefficient of restitution of particles colliding with surfaces in air and water. Adv. Powder Technol. 2020, 31, 3747–3759. [Google Scholar] [CrossRef]
- Horabik, J.; Beczek, M.; Mazur, R.; Parafifiniuk, P.; Ryzak, M.; Molenda, M. Determination of the restitution coefficient of seeds and coefficient of visco-elastic Hertz contact models for DEM simulations. Biosyst. Eng. 2017, 161, 106–119. [Google Scholar] [CrossRef]
- Available online: https://www.edemsimulation.com/forum/EDEM[EB/OL] (accessed on 15 January 2023).
- Nafsun, A.I.; Herz, F.; Specht, E.; Komossa, H.; Wirtz, S.; Scherer, V.; Liu, X. Thermal bed mixing in rotary drums for different operational parameters. Chem. Eng. Sci. 2017, 160, 346–353. [Google Scholar] [CrossRef]
- Mellmann, J. The transverse motion of solids in rotating cylinders—Forms of motion and transition behavior. Powder Technol. 2001, 118, 251–270. [Google Scholar] [CrossRef]


























| Variety | Size/mm | Mean/mm | Standard Deviation/mm |
|---|---|---|---|
| Jinong 1 | Length (L) | 9.63 | 0.54 |
| Width (W) | 9.11 | 1.19 | |
| Thickness (T) | 7.94 | 1.43 | |
| Jinong 2 | Length (L) | 8.02 | 0.62 |
| Width (W) | 13.70 | 1.71 | |
| Thickness (T) | 5.80 | 0.65 | |
| Jinong 3 | Length (L) | 11.86 | 1.37 |
| Width (W) | 11.45 | 1.56 | |
| Thickness (T) | 9.49 | 1.56 |
| Time | Type | Size Before Hydroponic Culture | Size After Hydroponic Culture | Size Growth Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L/mm | W/mm | T/mm | L′/mm | W′/mm | T′/mm | (L′ − L)/L | (W′ − W)/W | (T′ − T)/T | ||
| 12 h | Jinong 1 | 9.21 | 8.62 | 7.41 | 9.59 | 9.37 | 8.60 | 4.13% | 8.70% | 16.06% |
| Jinong 2 | 8.17 | 13.83 | 5.04 | 8.73 | 14.49 | 5.68 | 6.85% | 4.77% | 12.70% | |
| Jinong 3 | 12.19 | 11.32 | 9.28 | 12.49 | 11.91 | 9.74 | 2.46% | 5.21% | 4.96% | |
| 24 h | Jinong 1 | 9.148 | 9.33 | 7.24 | 10.07 | 9.57 | 8.96 | 10.08% | 2.57% | 23.76% |
| Jinong 2 | 7.99 | 13.35 | 6.17 | 8.34 | 14.20 | 7.26 | 4.38% | 6.37% | 17.67% | |
| Jinong 3 | 11 | 8.95 | 9.88 | 12.01 | 9.64 | 10.93 | 9.18% | 7.71% | 10.63% | |
| 36 h | Jinong 1 | 10.03 | 7.45 | 7.89 | 10.61 | 9.59 | 9.70 | 5.78% | 28.72% | 22.94% |
| Jinong 2 | 7.66 | 13.87 | 5.55 | 8.21 | 14.88 | 7.01 | 7.18% | 7.28% | 26.31% | |
| Jinong 3 | 11.51 | 11.29 | 9.13 | 12.46 | 11.80 | 10.63 | 8.25% | 4.52% | 16.43% | |
| 48 h | Jinong 1 | 9.05 | 7.4 | 8.37 | 10.63 | 9.39 | 9.95 | 17.46% | 26.89% | 18.88% |
| Jinong 2 | 7.55 | 15.81 | 4.90 | 8.85 | 17.40 | 7.93 | 17.22% | 10.06% | 61.84% | |
| Jinong 3 | 12.9 | 9.9 | 11.53 | 13.90 | 11.88 | 13.33 | 7.75% | 20.00% | 15.61% | |
| Jinong 1 | Jinong 2 | Jinong 3 | |||
|---|---|---|---|---|---|
| Moisture Content | Young’s Modulus /Mpa | Moisture Content | Young’s Modulus /Mpa | Moisture Content | Young’s Modulus /Mpa |
| 29% | 2.99 | 32% | 3.97 | 38% | 312 |
| 40% | 2.69 | 38% | 3.11 | 39% | 135 |
| 42% | 1.05 | 40% | 1.19 | 40% | 8.92 |
| 50% | 0.55 | 57% | 0.52 | 46% | 5.68 |
| Variety | Filing Method | Number of Filing Spheres | Volume/m3 | Volume Ratio |
|---|---|---|---|---|
| Jinong 1 | Manual filing | 7-Sphere | 3.5746 × 10−7 | 103.68% |
| 9-Sphere | 3.21057 × 10−7 | 93.12% | ||
| 11-Sphere | 3.47738 × 10−7 | 100.86% | ||
| Automatic filing | 11-Sphere | 3.5734 × 10−7 | 103.64% | |
| 188-Sphere | 3.6420 × 10−7 | 105.63% | ||
| 1811-Sphere | 3.4479 × 10−7 | 100.00% | ||
| Jinong 2 | Manual filing | 9-Sphere | 3.0109 × 10−7 | 85.79% |
| 11-Sphere | 3.5378 × 10−7 | 100.80% | ||
| 13-Sphere | 3.7178 × 10−7 | 105.93% | ||
| Automatic filing | 13-Sphere | 3.7143 × 10−7 | 105.83% | |
| 170-Sphere | 3.8468 × 10−7 | 100.00% | ||
| 1650-Sphere | 3.5097 × 10−7 | 100.00% | ||
| Jinong 3 | Manual filing | 7-Sphere | 6.5727 × 10−7 | 102.66% |
| 9-Sphere | 6.4211 × 10−7 | 100.29% | ||
| 11-Sphere | 6.4029 × 10−7 | 100.01% | ||
| Automatic filing | 11-Sphere | 6.4789 × 10−7 | 101.20% | |
| 181-Sphere | 6.6884 × 10−7 | 104.47% | ||
| 1782-Sphere | 6.4023 × 10−7 | 100.00% |
| Variety | Mean/mm | Standard Deviation/mm |
|---|---|---|
| Jinong 1 | 9.1098 | 1.1916 |
| Jinong 2 | 13.695 | 1.7046 |
| Jinong 3 | 11.452 | 1.5552 |
| Parameter | Jinong 1 | Jinong 2 | Jinong 3 | Polymethyl Methacrylate | Steel | Copper |
|---|---|---|---|---|---|---|
| Poisson’s ratio | 0.4 | 0.4 | 0.4 | 0.32 | 0.3 | 0.35 |
| Density, kg/m3 | 1340 | 1270 | 1190 | 1190 | 7850 | 8960 |
| Young’ s modulus, MPa | 165 | 165 | 165 | 1197 | 20,000 | 100 |
| Coefficient of restitution | 0.45 | 0.45 | 0.45 | 0.55 | 0.65 | 0.5 |
| Coefficient of static friction | 0.55 | 0.35 | 0.35 | 0.34 | 0.4 | 0.4 |
| Coefficient of rolling friction | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Zhang, R.; Jiang, X.; Feng, W.; Wang, Y.; Wang, J. Study on Verification Approach and Multicontact Points Issue When Modeling Cyperus esculentus Seeds Based on DEM. Processes 2023, 11, 825. https://doi.org/10.3390/pr11030825
Xu T, Zhang R, Jiang X, Feng W, Wang Y, Wang J. Study on Verification Approach and Multicontact Points Issue When Modeling Cyperus esculentus Seeds Based on DEM. Processes. 2023; 11(3):825. https://doi.org/10.3390/pr11030825
Chicago/Turabian StyleXu, Tianyue, Ruxin Zhang, Xinming Jiang, Weizhi Feng, Yang Wang, and Jingli Wang. 2023. "Study on Verification Approach and Multicontact Points Issue When Modeling Cyperus esculentus Seeds Based on DEM" Processes 11, no. 3: 825. https://doi.org/10.3390/pr11030825
APA StyleXu, T., Zhang, R., Jiang, X., Feng, W., Wang, Y., & Wang, J. (2023). Study on Verification Approach and Multicontact Points Issue When Modeling Cyperus esculentus Seeds Based on DEM. Processes, 11(3), 825. https://doi.org/10.3390/pr11030825