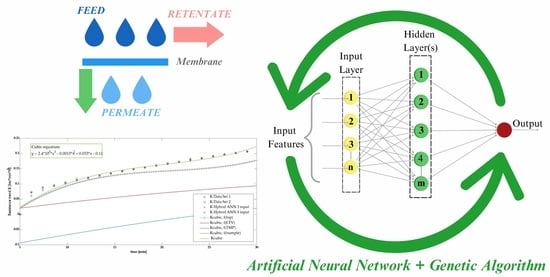
Application of Artificial Neural Networks for Modelling and Control of Flux Decline in Cross-Flow Whey Ultrafiltration
Abstract
:1. Introduction
1.1. Membrane Applications in the Dairy Industry
1.2. ANN in Membrane Technologies
1.3. The Genetic Algorithm as the Optimization Algorithm
2. Materials and Methods
2.1. Neural Network Design
- Taking and multiplying some numeric inputs by adjustable parameters called weights produces weighted inputs, and adds a scalar parameter called bias or a threshold value to the result:where and are the input signals and weights, respectively; while represents the threshold value or the bias term.
- The calculation of the output of the neuron by applying a transfer or “activation function” on the result, which has the net input signal as the argument:
2.2. A Hybrid Serial Architecture Model for the Evaluation of Resistances
2.3. Neural Network Optimization
3. Results
3.1. ANN Model Performance
3.2. K-Resistance Trends from the Hybrid Model
3.3. Optimization Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reig, M.; Vecino, X.; Cortina, J.L. Use of Membrane Technologies in Dairy Industry: An Overview. Foods 2021, 10, 2768. [Google Scholar] [CrossRef] [PubMed]
- Papaioannou, E.H.; Mazzei, R.; Bazzarelli, F.; Piacentini, E.; Giannakopoulos, V.; Roberts, M.R.; Giorno, L. Agri-Food Industry Waste as Resource of Chemicals: The Role of Membrane Technology in Their Sustainable Recycling. Sustainbility 2022, 14, 1483. [Google Scholar] [CrossRef]
- Gaudio, M.T.; Curcio, S.; Chakraborty, S. Design of an Integrated Membrane System to Produce Dairy By-Product from Waste Processing. Int. J. Food Sci. Technol. 2023, 58, 2104–2114. [Google Scholar] [CrossRef]
- Ramos, O.L.; Pereira, R.N.; Rodrigues, R.M.; Teixeira, J.A.; Vicente, A.A.; Malcata, F.X. Whey and Whey Powders: Production and Uses. In Encyclopedia of Food and Health; Elsevier Inc.: Amsterdam, The Netherlands, 2015; pp. 498–505. ISBN 9780123849533. [Google Scholar]
- Monti, L.; Donati, E.; Zambrini, A.V.; Contarini, G. Application of Membrane Technologies to Bovine Ricotta Cheese Exhausted Whey (Scotta). Int. Dairy J. 2018, 85, 121–128. [Google Scholar] [CrossRef]
- Castro, B.N.; Gerla, P.E. Hollow Fiber and Spiral Cheese Whey Ultrafiltration: Minimizing Controlling Resistances. J. Food Eng. 2005, 69, 495–502. [Google Scholar] [CrossRef]
- Daufin, G.; Escudier, J.P.; Carrère, H.; Bérot, S.; Fillaudeau, L.; Decloux, M. Recent and Emerging Applications of Membrane Processes in the Food and Dairy Industry. Food Bioprod. Process. Trans. Inst. Chem. Eng. Part C 2001, 79, 89–102. [Google Scholar] [CrossRef]
- Cui, Z.F.; Jiang, Y.; Field, R.W. Fundamentals of Pressure-Driven Membrane Separation Processes. In Membrane Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2010; pp. 1–18. ISBN 9781856176323. [Google Scholar]
- Niemi, H.; Bulsari, A.; Palosaari, S. Simulation of Membrane Separation by Neural Networks. J. Memb. Sci. 1995, 102, 185–191. [Google Scholar] [CrossRef]
- Razavi, M.A.; Mortazavi, A.; Mousavi, M. Dynamic Modelling of Milk Ultrafiltration by Artificial Neural Network. J. Memb. Sci. 2003, 220, 47–58. [Google Scholar] [CrossRef]
- Rai, P.; Majumdar, G.C.; DasGupta, S.; De, S. Modeling the Performance of Batch Ultrafiltration of Synthetic Fruit Juice and Mosambi Juice Using Artificial Neural Network. J. Food Eng. 2005, 71, 273–281. [Google Scholar] [CrossRef]
- Curcio, S.; Calabrò, V.; Iorio, G. Reduction and Control of Flux Decline in Cross-Flow Membrane Processes Modeled by Artificial Neural Networks. J. Memb. Sci. 2006, 286, 125–132. [Google Scholar] [CrossRef]
- Chen, H.; Kim, A.S. Prediction of Permeate Flux Decline in Crossflow Membrane Filtration of Colloidal Suspension: A Radial Basis Function Neural Network Approach. Desalination 2006, 192, 415–428. [Google Scholar] [CrossRef]
- Sarkar, B.; Sengupta, A.; De, S.; DasGupta, S. Prediction of Permeate Flux during Electric Field Enhanced Cross-Flow Ultrafiltration—A Neural Network Approach. Sep. Purif. Technol. 2009, 65, 260–268. [Google Scholar] [CrossRef]
- Guadix, A.; Zapata, J.E.; Almecija, M.C.; Guadix, E.M. Predicting the Flux Decline in Milk Cross-Flow Ceramic Ultrafiltration by Artificial Neural Networks. Desalination 2010, 250, 1118–1120. [Google Scholar] [CrossRef]
- Madaeni, S.S.; Hasankiadeh, N.T.; Tavakolian, H.R. Modeling and Optimization of Membrane Chemical Cleaning by Artificial Neural Network, Fuzzy Logic, and Genetic Algorithm. Chem. Eng. Commun. 2012, 199, 399–416. [Google Scholar] [CrossRef]
- Yangali-Quintanilla, V.; Verliefde, A.; Kim, T.U.; Sadmani, A.; Kennedy, M.; Amy, G. Artificial Neural Network Models Based on QSAR for Predicting Rejection of Neutral Organic Compounds by Polyamide Nanofiltration and Reverse Osmosis Membranes. J. Memb. Sci. 2009, 342, 251–262. [Google Scholar] [CrossRef]
- Rahmanian, B.; Pakizeh, M.; Mansoori, S.A.A.; Esfandyari, M.; Jafari, D.; Maddah, H.; Maskooki, A. Prediction of MEUF Process Performance Using Artificial Neural Networks and ANFIS Approaches. J. Taiwan Inst. Chem. Eng. 2012, 43, 558–565. [Google Scholar] [CrossRef]
- Soleimani, R.; Shoushtari, N.A.; Mirza, B.; Salahi, A. Experimental Investigation, Modeling and Optimization of Membrane Separation Using Artificial Neural Network and Multi-Objective Optimization Using Genetic Algorithm. Chem. Eng. Res. Des. 2013, 91, 883–903. [Google Scholar] [CrossRef]
- Delgrange, N.; Cabassud, C.; Cabassud, M.; Durand-Bourlier, L.; Lainé, J.M. Modelling of Ultrafiltration Fouling by Neural Network. Desalination 1998, 118, 213–227. [Google Scholar] [CrossRef]
- Badrnezhad, R.; Mirza, B. Modeling and Optimization of Cross-Flow Ultrafiltration Using Hybrid Neural Network-Genetic Algorithm Approach. J. Ind. Eng. Chem. 2014, 20, 528–543. [Google Scholar] [CrossRef]
- Cheryan, M.; Cheryan, M. Ultrafiltration and Microfiltration Handbook; Technomic Pub. Co.: Lancaster, PA, USA, 1998; ISBN 9781566765985. [Google Scholar]
- Samuelsson, G.; Huisman, I.H.; Trägårdh, G.; Paulsson, M. Predicting Limiting Flux of Skim Milk in Crossflow Microfiltration. J. Memb. Sci. 1997, 129, 277–281. [Google Scholar] [CrossRef]
- Saraceno, A.; Curcio, S.; Calabrò, V.; Iorio, G. A Hybrid Neural Approach to Model Batch Fermentation of “Ricotta Cheese Whey” to Ethanol. Comput. Chem. Eng. 2010, 34, 1590–1596. [Google Scholar] [CrossRef]
- Sivanandam, S.N.; Deepa, S.N. Genetic Algorithms. Introd. to Genet. Algorithms 2008. [Google Scholar] [CrossRef]
- Chow, T.T.; Zhang, G.Q.; Lin, Z.; Song, C.L. Global Optimization of Absorption Chiller System by Genetic Algorithm and Neural Network. Energy Build. 2002, 34, 103–109. [Google Scholar] [CrossRef]
- Madaeni, S.S.; Hasankiadeh, N.T.; Kurdian, A.R.; Rahimpour, A. Modeling and Optimization of Membrane Fabrication Using Artificial Neural Network and Genetic Algorithm. Sep. Purif. Technol. 2010, 76, 33–43. [Google Scholar] [CrossRef]
- Reihanian, M.; Asadullahpour, S.R.; Hajarpour, S.; Gheisari, K. Application of Neural Network and Genetic Algorithm to Powder Metallurgy of Pure Iron. Mater. Des. 2011, 32, 3183–3188. [Google Scholar] [CrossRef]
- Cong, T.; Su, G.; Qiu, S.; Tian, W. Applications of ANNs in Flow and Heat Transfer Problems in Nuclear Engineering: A Review Work. Prog. Nucl. Energy 2013, 62, 54–71. [Google Scholar] [CrossRef]
- Arefi-Oskoui, S.; Khataee, A.; Vatanpour, V. Modeling and Optimization of NLDH/PVDF Ultrafiltration Nanocomposite Membrane Using Artificial Neural Network-Genetic Algorithm Hybrid. ACS Comb. Sci. 2017, 19, 464–477. [Google Scholar] [CrossRef] [PubMed]
- Goli, A.; Zare, H.K.; Moghaddam, R.; Sadeghieh, A. A Comprehensive Model of Demand Prediction Based on Hybrid Artificial Intelligence and Metaheuristic Algorithms: A Case Study in Dairy Industry. SSRN Electron. J. 2018, 11, 190–203. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Mohammadi, A.H.; Belandria, V.; Richon, D. Use of an Artificial Neural Network Algorithm to Predict Hydrate Dissociation Conditions for Hydrogen+water and Hydrogen+tetra-n-Butyl Ammonium Bromide+water Systems. Chem. Eng. Sci. 2010, 65, 4302–4305. [Google Scholar] [CrossRef]
- Alamolhoda, S.; Kazemeini, M.; Zaherian, A.; Zakerinasab, M.R. Reaction Kinetics Determination and Neural Networks Modeling of Methanol Dehydration over Nano γ-Al2O3 Catalyst. J. Ind. Eng. Chem. 2012, 18, 2059–2068. [Google Scholar] [CrossRef]
- Istadi, I.; Amin, N.A.S. Modelling and Optimization of Catalytic–Dielectric Barrier Discharge Plasma Reactor for Methane and Carbon Dioxide Conversion Using Hybrid Artificial Neural Network—Genetic Algorithm Technique. Chem. Eng. Sci. 2007, 62, 6568–6581. [Google Scholar] [CrossRef]
- Lahiri, S.K.; Ghanta, K.C. Development of an Artificial Neural Network Correlation for Prediction of Hold-up of Slurry Transport in Pipelines. Chem. Eng. Sci. 2008, 63, 1497–1509. [Google Scholar] [CrossRef]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2008; ISBN 9780071422949. [Google Scholar]









| Activation Function Name | Function Name in Matlab Code | Equation |
|---|---|---|
| Linear | purelin | |
| Hyperbolic tangent | tansig | |
| Log-sigmoid | logsig | |
| Radial basis | radbas | |
| Triangular basis | tribas |
| Boundary Constraints | Operating Time top (min) | Sampling Time tsample (min) | Cross-Flow Velocity CFV (L/min) | Transmembrane Pressure TMP (bar) |
|---|---|---|---|---|
| Lower | 30 | 5 | 5 | 0.5 |
| Upper | 330 | 30 | 10 | 5 |
| Scenario | Neurons in Hidden Layer 1 | Neurons in Hidden Layer 2 | MSE | Training Performance | Validation Performance | Test Performance | R |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 6 | 2.40 × 10−3 | 3.11 × 10−3 | 1.40 × 10−3 | 6.63 × 10−1 | 0.95676 |
| 2 | 7 | 7 | 2.64 × 10−5 | 2.82 × 10−5 | 1.42 × 10−1 | 2.89 × 10−1 | 0.99918 |
| 3 | 8 | 0 | 1.30 × 10−3 | 3.43 × 10−5 | 1.30 × 10−3 | 4.22 × 10−5 | 0.99274 |
| 4 | 8 | 8 | 1.60 × 10−5 | 1.10 × 10−5 | 1.10 × 10−5 | 4.66 × 10−5 | 0.99952 |
| 5 | 8 | 9 | 5.42 × 10−4 | 7.54 × 10−4 | 3.14 × 10−5 | 5.05 × 10−5 | 0.98395 |
| 6 | 8 | 10 | 1.52 × 10−4 | 1.94 × 10−4 | 3.11 × 10−5 | 7.02 × 10−1 | 0.99759 |
| 7 | 9 | 9 | 1.09 × 10−4 | 1.15 × 10−4 | 4.83 × 10−1 | 1.43 | 0.99854 |
| 8 | 10 | 10 | 2.44 × 10−5 | 2.34 × 10−5 | 4.50 × 10−1 | 1.09 × 10−1 | 0.99924 |
| Scenario | Neurons in Hidden Layer 1 | Neurons in Hidden Layer 2 | MSE | Training Performance | Validation Performance | Test Performance | R |
|---|---|---|---|---|---|---|---|
| 1 | 8 | 0 | 4.09 × 10−2 | 1.63 × 10−5 | 4.09 × 10−2 | 1.49 × 10−5 | 0.89667 |
| 2 | 8 | 8 | 2.91 × 10−4 | 3.76 × 10−4 | 1.35 × 10−4 | 3.58 × 10−5 | 0.99239 |
| 3 | 8 | 9 | 2.81 × 10−4 | 7.49 × 10−6 | 8.26 × 10−6 | 1.76 × 10−3 | 0.99233 |
| 4 | 8 | 10 | 5.29 × 10−4 | 1.16 × 10−5 | 3.68 × 10−3 | 6.03 × 10−5 | 0.98350 |
| 5 | 9 | 0 | 7.15 × 10−4 | 9.85 × 10−4 | 1.81 × 10−4 | 6.11 × 10−5 | 0.97828 |
| 6 | 9 | 9 | 3.88 × 10−5 | 8.07 × 10−6 | 6.06 × 10−6 | 2.07 × 10−4 | 0.99882 |
| 7 | 10 | 0 | 1.02 × 10−4 | 1.40 × 10−4 | 8.58 × 10−6 | 2.81 × 10−5 | 0.99720 |
| 8 | 10 | 10 | 5.38 × 10−4 | 7.28 × 10−4 | 2.88 × 10−5 | 1.40 × 10−4 | 0.98433 |
| Neurons in the Input Layer | Neurons in Hidden Layer 1 | Neurons in Hidden Layer 2 | Data Set | MSE |
|---|---|---|---|---|
| 3 | 8 | 8 | 1 | 0.035 |
| 3 | 8 | 8 | 2 | 0.005 |
| 4 | 9 | 9 | 1 | 0.042 |
| 4 | 9 | 9 | 2 | 0.002 |
| ANN Inputs | Minimum MSE | Optimal Operating Conditions | ||||
|---|---|---|---|---|---|---|
| Operating Time top (min) | Sampling Time tsample (min) | Cross-Flow Velocity CFV (L/min) | Transmembrane Pressure TMP (bar) | Normalized Permeate Flux (%) | ||
| 3 | 2.89 × 10−13 | 300 | 8.33 | 8.33 | - | 1.00 |
| 4 | 1.71 × 10−11 | 225 | 15.9 | 6.25 | 1.33 | 7.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaudio, M.T.; Curcio, S.; Chakraborty, S.; Calabrò, V. Application of Artificial Neural Networks for Modelling and Control of Flux Decline in Cross-Flow Whey Ultrafiltration. Processes 2023, 11, 1287. https://doi.org/10.3390/pr11041287
Gaudio MT, Curcio S, Chakraborty S, Calabrò V. Application of Artificial Neural Networks for Modelling and Control of Flux Decline in Cross-Flow Whey Ultrafiltration. Processes. 2023; 11(4):1287. https://doi.org/10.3390/pr11041287
Chicago/Turabian StyleGaudio, Maria Teresa, Stefano Curcio, Sudip Chakraborty, and Vincenza Calabrò. 2023. "Application of Artificial Neural Networks for Modelling and Control of Flux Decline in Cross-Flow Whey Ultrafiltration" Processes 11, no. 4: 1287. https://doi.org/10.3390/pr11041287
APA StyleGaudio, M. T., Curcio, S., Chakraborty, S., & Calabrò, V. (2023). Application of Artificial Neural Networks for Modelling and Control of Flux Decline in Cross-Flow Whey Ultrafiltration. Processes, 11(4), 1287. https://doi.org/10.3390/pr11041287