Kinetics of the Aqueous-Phase Copolymerization of MAA and PEGMA Macromonomer: Influence of Monomer Concentration and Side Chain Length of PEGMA
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Copolymerization Reactions
2.3. Estimation of Reactivity Ratios
3. Results and Discussion
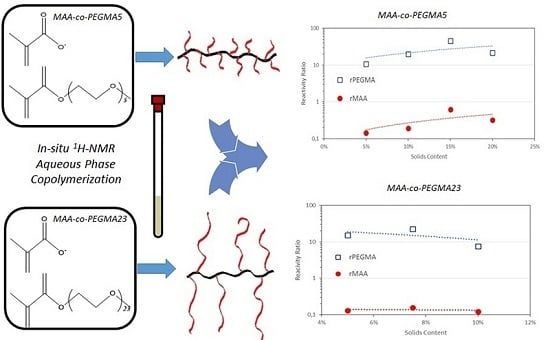
3.1. MAA-co-PEGMA5 (5 Ethylene Glycol Units)
3.2. MAA-co-PEGMA23 (23 Ethylene Glycol Units)
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smolne, S.; Weber, S.; Buback, M. Propagation and termination kinetics of poly(ethylene glycol) methyl ether methacrylate in aqueous solution. Macromol. Chem. Phys. 2016, 217, 2391–2401. [Google Scholar] [CrossRef]
- Neugebauer, D. Graft copolymers with poly(ethylene oxide) segments. Polym. Int. 2007, 56, 1469–1498. [Google Scholar] [CrossRef]
- Robinson, D.N.; Peppas, N.A. Preparation and characterization of pH-responsive poly (methacrylic acid-g-ethylene glycol) nanospheres. Macromolecules 2002, 35, 3668–3674. [Google Scholar] [CrossRef]
- Tuncel, A. Emulsion copolymerization of styrene and poly(ethylene glycol) ethyl ether methacrylate. Polymer 2000, 41, 1257–1267. [Google Scholar] [CrossRef]
- Halake, K.; Birajdar, M.; Kim, B.S.; Bae, H.; Lee, C.; Kim, Y.J.; Kim, S.; Kim, H.J.; Ahn, S.; An, S.Y.; et al. Recent application developments of water-soluble synthetic polymers. J. Ind. Eng. Chem. 2014, 20, 3913–3918. [Google Scholar] [CrossRef]
- Brown, R.; Stitzel, B.; Sauer, T. Steric stabilization by grafting and copolymerization of water soluble oligomers and polymers. Macromol. Chem. Phys. 1995, 196, 2047–2064. [Google Scholar] [CrossRef]
- Colombo, C.; Gatti, S.; Ferrari, R.; Casalini, T.; Cuccato, D.; Morosi, L.; Zucchetti, M.; Moscatelli, D. Self-assembling amphiphilic PEGylated block copolymers obtained through RAFT polymerization for drug-delivery applications. J. Appl. Polym. Sci. 2016, 133, 1–8. [Google Scholar] [CrossRef]
- Preusser, C.; Ezenwajiaku, I.H.; Hutchinson, R.A. The combined influence of monomer concentration and ionization on acrylamide/acrylic acid composition in aqueous solution radical batch copolymerization. Macromolecules 2016, 49, 4746–4756. [Google Scholar] [CrossRef]
- Amjad, Z. Water Soluble Polymers. Solution properties and applications; Kluwer Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Dautzenberg, H.; Jaeger, W.; Kötz, J.; Phillip, B.; Seidel, C.; Stscherbina, D. Polyelectrolytes: Formation, Characterisation and Application; Hauser Publishers: Munich, Germany, 1994. [Google Scholar]
- Yu., K.E. Water Soluble Poly-N-Vinylamides Synthesis and Physiochemical Properties; John Wiley and Sons Ltd.: Chichester, UK, 1998. [Google Scholar]
- Kricheldorf, H.R. Handbook of Polymer Synthesis; Mercel Dekker Inc.: New York, NY, USA, 1991. [Google Scholar]
- Lacik, I.; Beuermann, S.; Buback, M. PLP-SEC study into the free-radical propagation rate coefficients of partially and fully ionized acrylic acid in aqueous solution. Macromol. Chem. Phys. 2004, 205, 1080–1087. [Google Scholar] [CrossRef]
- Lacík, I.; Beuermann, S.; Buback, M. Aqueous phase size-exclusion-chromatography used for PLP-SEC studies into free-radical propagation rate of acrylic acid in aqueous solution. Macromolecules 2001, 34, 6224–6228. [Google Scholar] [CrossRef]
- Lacík, I.; Beuermann, S.; Buback, M. PLP-SEC study into free-radical propagation rate of nonionized acrylic acid in aqueous solution. Macromolecules 2003, 36, 9355–9363. [Google Scholar] [CrossRef]
- Cutie, S.S.; Smith, P.B.; Henton, D.E.; Staples, T.L.; Powell, C. Acrylic acid polymerization kinetics. J. Polym. Sci. Part A Polym. Chem. 1997, 35, 2029–2047. [Google Scholar] [CrossRef]
- Seabrook, S.A.; Tonge, M.P.; Gilbert, R.G. Pulsed laser polymerization study of the propagation kinetics of acrylamide in water. J. Polym. Sci. Part A Polym. Chem. 2005, 43, 1357–1368. [Google Scholar] [CrossRef]
- Lacík, I.; Chovancova, A.; Uhelsk, L.; Preusser, C.; Hutchinson, R.A.; Buback, M. PLP-SEC studies into the propagation rate coefficient of acrylamide radical polymerization in aqueous solution. Macromolecules 2016, 49, 3244–3253. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Hesse, P.; Lacík, I. Free-radical propagation rate coefficient of nonionized methacrylic acid in aqueous solution from low monomer concentrations to bulk polymerization. Macromolecules 2006, 39, 184–193. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Hesse, P.; Kukućková, S.; Lacík, I. Propagation rate coefficient of non-ionized methacrylic acid radical polymerization in aqueous solution. The effect of monomer conversion. Macromol. Symp. 2007, 248, 41–49. [Google Scholar] [CrossRef]
- Lacík, I.; Učňová, L.; Kukučková, S.; Buback, M.; Hesse, P.; Beuermann, S. Propagation rate coefficient of free-radical polymerization of partially and fully ionized methacrylic acid in aqueous solution. Macromolecules 2009, 42, 7753–7761. [Google Scholar] [CrossRef]
- Stach, M.; Lacík, I.; Chorvát, D.; Buback, M.; Hesse, P.; Hutchinson, R.A.; Tang, L. Propagation rate coefficient for radical polymerization of N-vinyl pyrrolidone in aqueous solution obtained by PLP-SEC. Macromolecules 2008, 41, 5174–5185. [Google Scholar] [CrossRef]
- Stach, M.; Lacík, I.; Kasák, P.; Chorvát, D.; Saunders, A.J.; Santanakrishnan, S.; Hutchinson, R.A. Free-radical propagation kinetics of N-vinyl formamide in aqueous solution studied by PLP-SEC. Macromol. Chem. Phys. 2010, 211, 580–593. [Google Scholar] [CrossRef]
- Santanakrishnan, S.; Hutchinson, R.A.; Učňová, L.; Stach, M.; Lacík, I.; Buback, M. Polymerization kinetics of water-soluble N-vinyl monomers in aqueous and organic solution. Macromol. Symp. 2011, 302, 216–223. [Google Scholar] [CrossRef]
- Buback, M.; Hesse, P.; Hutchinson, R.A.; Lacík, I.; Kasák, P.; Stach, M.; Utz, I. Kinetics and modeling of free-radical batch poymerization of nonionized methacrylic acid in aqueous solution. Ind. Eng. Chem. 2008, 47, 8197–8204. [Google Scholar] [CrossRef]
- Flatt, R.; Schober, I. Superplasticizers and the Rheology of Concrete 7. Understanding the Rheology of Concrete; Roussel, N., Ed.; Woodhead Publishing Limited: Oxford, UK, 2011. [Google Scholar]
- Marchon, D.; Sulser, U.; Eberhardt, A.; Flatt, R.J. Molecular design of comb-shaped polycarboxylate dispersants for environmentally friendly concrete. Soft Matter 2013, 9, 10719–10728. [Google Scholar] [CrossRef]
- Guicquero, J.P.; Maitrasse, P.; Mosquet, M.A.; Alphonse, S. A Water Soluble or Water Dispersible Dispersing Agent. FR2776285, 19 March 1998. [Google Scholar]
- Lei, L.; Plank, J. Synthesis and properties of a vinyl ether-based polycarboxylate superplasticizer for concrete possessing clay tolerance. Ind. Eng. Chem. Res. 2014, 53, 1048–1055. [Google Scholar] [CrossRef]
- Plank, J.; Pöllmann, K.; Zouaoui, N.; Andres, P.R.; Schaefer, C. Synthesis and performance of methacrylic ester based polycarboxylate superplasticizers possessing hydroxy terminated poly(ethylene glycol) side chains. Cem. Concr. Res. 2008, 38, 1210–1216. [Google Scholar] [CrossRef]
- Plank, J.; Sakai, E.; Miao, C.W.; Yu, C.; Hong, J.X. Chemical admixtures—Chemistry, applications and their impact on concrete microstructure and durability. Cem. Concr. Res. 2015, 78, 81–99. [Google Scholar] [CrossRef]
- Pourchet, S.; Liautaud, S.; Rinaldi, D.; Pochard, I. Effect of the repartition of the PEG side chains on the adsorption and dispersion behaviors of PCP in presence of sulfate. Cem. Concr. Res. 2012, 42, 431–439. [Google Scholar] [CrossRef]
- Smith, B.L.; Klier, J. Determination of monomer reactivity ratios for copolymerizations of methacrylic acid with poly(ethylene glycol) monomethacrylate. J. Appl. Polym. Sci. 1998, 68, 1019–1025. [Google Scholar] [CrossRef]
- Georges, S.; Hamaide, T. Determination of the reactivity ratios of the methacrylic acid-polyethylene glycol methacrylate system by aqueous SEC. Bul. Stiint. al Univ. “Politehnica” din Timisoara 2001, 46, 187–191. [Google Scholar]
- Krivorotova, T.; Vareikis, A.; Gromadzki, D.; Netopilík, M.; Makuška, R. Conventional free-radical and RAFT copolymerization of poly(ethylene oxide) containing macromonomers. Eur. Polym. J. 2010, 46, 546–556. [Google Scholar] [CrossRef]
- Najafi, V.; Ziaee, F.; Kabiri, K.; Mehr, M.J.Z.; Abdollahi, H.; Nezhad, P.M.; Jalilian, S.M.; Nouri, A. Aqueous free-radical polymerization of PEGMEMA macromer: Kinetic studies via an on-line 1H NMR technique. Iran. Polym. J. Engl. Ed. 2012, 21, 683–688. [Google Scholar] [CrossRef]
- Fukuda, T.; Inagaki, H. Free-Radical Copolymerization. 3. Determination of rate constants of propagation and termination for the styrene/methyl methacrylate system. A critical test of terminal-model kinetics 1. Macromolecules 1985, 18, 17–26. [Google Scholar] [CrossRef]
- Coote, M.L.; Davis, T.P. Mechanism of the propagation step in free-radical copolymerisation. Prog. Polym. Sci. 1999, 24, 1217–1251. [Google Scholar] [CrossRef]
- Olaj, O.F.; Schnöll-Bitai, I.; Kremminger, P. Evaluation of individual rate constants from the chain-length distribution of polymer samples prepared by intermittent (rotating sector) photopolymerization-2. The copolymerization system styrene-methyl methacrylate. Eur. Polym. J. 1989, 25, 535–541. [Google Scholar] [CrossRef]
- De La Cal, J.C.; Leiza, J.R.; Asúa, J.M. Estimation of reactivity ratios using emulsion copolymerization data. J. Polym. Sci. Part A Polym. Chem. 1991, 29, 155–167. [Google Scholar] [CrossRef]
- García, G. Síntesis de Floculantes Catiónicos en Reactores Continuos. Ph.D. Thesis, University of the Basque Country (UPV/EHU), Donostia-San Sebastián, Spain, 2009. [Google Scholar]
- Beuermann, S.; Buback, M.; Hesse, P.; Hutchinson, R.A.; Kukučková, S.; Lacík, I. Termination kinetics of the free-radical polymerization of nonionized methacrylic acid in aqueous solution. Macromolecules 2008, 41, 3513–3520. [Google Scholar] [CrossRef]
- Riahinezhad, M.; Mcmanus, N.; Penlidis, A. Effect of monomer concentration and pH on reaction kinetics and copolymer microstructure of Acrylamide/Acrylic acid copolymer. Macromol. React. Eng. 2015, 9, 100–113. [Google Scholar] [CrossRef]
- Paril, A.; Alb, A.M.; Giz, A.T.; Çatagil-Giz, H. Effect of medium pH on the reactivity ratios in acrylamide acrylic acid copolymerization. J. Appl. Polym. Sci. 2007, 103, 968–974. [Google Scholar] [CrossRef]
- Ponratnam, S.; Kapur, S.L. Reactivity ratios of ionizing monomers in aqueous solution. Copolymerization of acrylic and methacrylic acids with acrylamide. Makromol. Chem. 1977, 178, 1029–1038. [Google Scholar] [CrossRef]
- Cabaness, W.R.; Lin, T.Y.-C.; Párkányi, C. Effect on the pH on the reactivity ratios in the copolymerization of acrylic acid and acrylamide. J. Polym. Sci. Part A Polym. Chem. 1971, 9, 2155–2170. [Google Scholar] [CrossRef]







© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emaldi, I.; Hamzehlou, S.; Sanchez-Dolado, J.; Leiza, J.R. Kinetics of the Aqueous-Phase Copolymerization of MAA and PEGMA Macromonomer: Influence of Monomer Concentration and Side Chain Length of PEGMA. Processes 2017, 5, 19. https://doi.org/10.3390/pr5020019
Emaldi I, Hamzehlou S, Sanchez-Dolado J, Leiza JR. Kinetics of the Aqueous-Phase Copolymerization of MAA and PEGMA Macromonomer: Influence of Monomer Concentration and Side Chain Length of PEGMA. Processes. 2017; 5(2):19. https://doi.org/10.3390/pr5020019
Chicago/Turabian StyleEmaldi, Iñaki, Shaghayegh Hamzehlou, Jorge Sanchez-Dolado, and Jose R. Leiza. 2017. "Kinetics of the Aqueous-Phase Copolymerization of MAA and PEGMA Macromonomer: Influence of Monomer Concentration and Side Chain Length of PEGMA" Processes 5, no. 2: 19. https://doi.org/10.3390/pr5020019
APA StyleEmaldi, I., Hamzehlou, S., Sanchez-Dolado, J., & Leiza, J. R. (2017). Kinetics of the Aqueous-Phase Copolymerization of MAA and PEGMA Macromonomer: Influence of Monomer Concentration and Side Chain Length of PEGMA. Processes, 5(2), 19. https://doi.org/10.3390/pr5020019