A New Method for the Process Division and Effect Evaluation of Coagulation Based on Particle Size Fractal Dimension
Abstract
:1. Introduction
2. Materials and Methods
2.1. Apparatus and Materials
2.2. Procedure and Method
3. Results and Discussion
3.1. Coagulation Effect Measured by the Quality of the Settled Water
3.2. Change in Particle Size Distribution during Coagulation
3.2.1. Particle Number
3.2.2. Particle Size Fractal Dimension
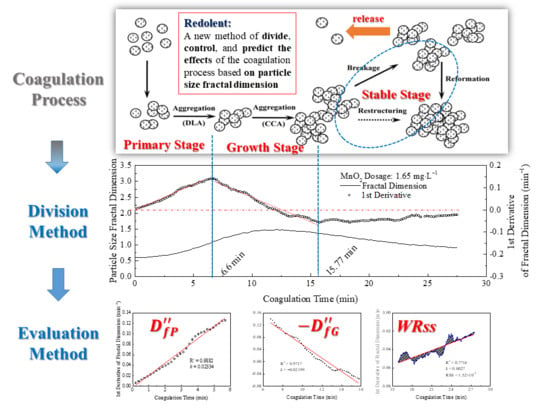
3.3. Coagulation Process Division Based on the Rate of Change in the Particle Size Fractal Dimension
3.3.1. Division of Coagulation Process
3.3.2. Rate of Change in Particle Size Fractal Dimension
3.4. Relationship Between Coagulation and Sedimentation
3.4.1. Time Parameters
3.4.2. Particle Size Distribution Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Razali, M.; Kim, J.F.; Attfield, M.P.; Budd, P.M.; Drioli, E.; Lee, Y.M.; Szekely, G. Sustainable wastewater treatment and recycling in membrane manufacturing. Green Chem. 2015, 17, 5196–5205. [Google Scholar] [CrossRef] [Green Version]
- Li, W.W.; Yu, H.Q.; He, Z. Towards sustainable wastewater treatment by using microbial fuel cells-centered technologies. Energy Environ. Sci. 2014, 7, 911–924. [Google Scholar] [CrossRef]
- Templeton, M.R.; Cantwell, R.E.; Quinn, C.; Hofmann, R.; Andrews, R.C. Pilot-scale assessment of the impacts of transient particulate water quality events on the UV disinfection of indigenous total coliform bacteria in drinking water treatment. J. Water Supply Res. Technol. 2009, 58, 11–20. [Google Scholar] [CrossRef]
- Strandman, S.; Vachon, R.; Dini, M.; Giasson, S.; Zhu, X.X. Polyacrylamides revisited: Flocculation of kaolin suspensions and mature fine tailings. Can. J. Chem. Eng. 2017, 96, 20–26. [Google Scholar] [CrossRef]
- Liang, H.; Tian, J.Y.; He, W.J.; Han, H.D.; Chen, Z.L.; Li, G.B. Combined preoxidation by permanganate and chlorine in enhancing the treatment of surface water. J. Chem. Technol. Biot. 2009, 84, 1229–1233. [Google Scholar] [CrossRef]
- Liu, R.P.; Sun, L.H.; Ju, R.; Wang, H.J.; Liu, H.J.; Gu, J.N.; Li, G.B. Effect of hydrous manganese dioxide on the treatment of low-turbidity source water: Plant-scale experience. J. Environ. Eng. 2011, 137, 481–486. [Google Scholar] [CrossRef]
- Li, H.Y.; Nan, J. Micro analysis of efficacy and mechanism of aid-coagulation with hydrated MnO2. In Proceedings of the 2009 International Conference on Energy and Environment Technology, Guilin, China, 16–18 October 2009; pp. 623–628. [Google Scholar] [CrossRef]
- Valtcheva, I.B.; Marchetti, P.; Livingston, A.G. Crosslinked polybenzimidazole membranes for organic solvent nanofiltration (OSN): Analysis of crosslinking reaction mechanism and effects of reaction parameters. J. Membr. Sci. 2015, 493, 568–579. [Google Scholar] [CrossRef]
- Didaskalou, C.; Kupai, J.; Cseri, L.; Barabas, J.; Vass, E.; Holtzl, T.; Szekely, G. Membrane-grafted asymmetric organocatalyst for an integrated synthesis-separation platform. ACS Catal. 2018, 8, 7430–7438. [Google Scholar] [CrossRef]
- Jiang, J.Q. The role of coagulation in water treatment. Curr. Opin. Chem. Eng. 2015, 8, 36–44. [Google Scholar] [CrossRef]
- Kuśnierz, M.; Wiercik, P. Analysis of particle size and fractal dimensions of suspensions contained in raw sewage, treated sewage and activated sludge. Arch. Environ. Prot. 2016, 42, 67–76. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.C.; Gao, B.Y.; Yue, Q.Y.; Wang, Y.; Li, W.W.; Zhu, X.B. Comparison of coagulation behavior and floc structure characteristic of different polyferric-cationic polymer dual-coagulants in humic acid solution. Water Res. 2009, 43, 724–732. [Google Scholar] [CrossRef] [PubMed]
- He, W.P.; Nan, J.; Li, H.Y.; Li, S.N. Characteristic analysis on temporal evolution of floc size and structure in low-shear flow. Water Res. 2012, 46, 509–520. [Google Scholar] [CrossRef] [PubMed]
- Du, L.G.; Bonner, J.S.; Garton, L.S.; Ernest, A.N.S.; Autenrieth, R.L. Modeling coagulation kinetics incorporating fractal theories: A fractal rectilinear approach. Water Res. 2000, 34, 1987–2000. [Google Scholar] [CrossRef]
- Du, L.G.; Bonner, J.S.; Garton, L.S.; Ernest, A.N.S.; Autenrieth, R.L. Modeling coagulation kinetics incorporating fractal theories: Comparison with observed data. Water Res. 2002, 36, 1056–1066. [Google Scholar] [CrossRef] [PubMed]
- Gregory, J. Monitoring particle aggregation processes. Adv. Colloid Interface Sci. 2009, 147–148, 109–123. [Google Scholar] [CrossRef] [PubMed]
- Vahedi, A.; Gorczyca, B. Predicting the settling velocity of flocs formed in water treatment using multiple fractal dimensions. Water Res. 2012, 46, 4188–4194. [Google Scholar] [CrossRef] [PubMed]
- Kilander, J.; Blomström, S.; Rasmuson, A. Spatial and temporal evolution of floc size distribution in a stirred square tank investigated using PIV and image analysis. Chem. Eng. Sci. 2006, 61, 7651–7667. [Google Scholar] [CrossRef]
- Margaritis, K.; Athanasios, G.K. Evolution of aggregate size and fractal dimension during Brownian coagulation. J. Aerosol Sci. 2001, 32, 1399–1420. [Google Scholar] [CrossRef]
- Amjad, H.; Khan, Z. A comparison of fractal dimensions of clay and humic acid flocs under optimum coagulation conditions. Int. J. Environ. Sci. Dev. 2016, 7, 240–243. [Google Scholar] [CrossRef]
- Li, D.S.; Cheng, G.D. Experimental study on treatment of high turbidity water from Yellow River by the technology of enhanced swirling clarifier. Chin. J. Environ. Eng. 2008, 2, 214–219. [Google Scholar]
- Gao, L.Q.; Zhang, Y.F.; Zhang, Z.H.; Yang, L.Y.; Jing, Q.N. Optimizing selection of coagulant for treatment of low temperature raw water of Tianjin Haihe River. J. Tianjin Polytech. Univ 2008, 27, 41–43. [Google Scholar] [CrossRef]
- Cong, H.B.; Sun, F.; Chen, W.J.; Xu, Y.J.; Wang, W. Study on the method and mechanism of pre-pressure coagulation and sedimentation for microcystis removal from drinking-water sources. Environ. Technol. 2017, 39, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Logan, B.E.; Kilps, J.R. Fractal dimensions of aggregates formed in different fluid mechanical environments. Water Res. 1995, 29, 443–453. [Google Scholar] [CrossRef]
- Zhu, Z.F.; Peng, D.Z.; Dou, J. Changes in the two-dimensional and perimeter-based fractal dimensions of kaolinite flocs during flocculation: A simple experimental study. Water Sci. Technol. 2018, 77, 861–870. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.S.; Wu, R.B.; Jiang, Y.Z.; Chow, C.W.K. Characterization of floc structure and strength: Role of changing shear rates under various coagulation mechanisms. Colloids Surf. A Physicochem. Eng. Asp. 2011, 379, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.Z.; Gregory, J.; Yang, Y.L.; Sun, M.; Liu, T.; Li, G.B. Effect of coagulation and applied breakage shear on the regrowth of kaolin flocs. Environ. Eng. Sci. 2010, 27, 483–492. [Google Scholar] [CrossRef]
- Boer, D.H.D.; Stone, M.; Lévesque, L.M.J. Fractal dimensions of individual flocs and floc populations in streams. Hydrol. Process. 2000, 14, 653–667. [Google Scholar] [CrossRef]
- Lin, Q.T.; Peng, H.L.; Lin, Q.L.; Yin, G.C. Formation, breakage and re-formation of flocs formed by cationic starch. Water Sci. Technol. 2013, 68, 1352–1358. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.W.; Yang, Y.L.; Li, X.; Wang, W.Q.; Wu, Y.; Wang, C.Y.; Luo, J.L. Coagulation performance and flocs characteristics of recycling pre-sonicated condensate sludge for low-turbidity surface water treatment. Sep. Purif. Technol. 2014, 123, 1–8. [Google Scholar] [CrossRef]
- Gonzalez-Torres, A.; Putnam, J.; Jefferson, B.; Stuetz, R.M.; Henderson, R.K. Examination of the physical properties of microcystis aeruginosa, flocs produced on coagulation with metal salts. Water Res. 2014, 60, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Zhao, J.H.; Xu, C.; Liu, M.L. Experimental analysis of magnesium hydroxide-reactive orange floc formation time and rate in coagulation process. J. Taiwan Inst. Chem. Eng. 2014, 45, 2605–2609. [Google Scholar] [CrossRef]










| Channel | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Particle Size (µm) | 2~3 | 3~4 | 4~5 | 5~6 | 6~7 | 7~8 | 8~600 |
| No. | Y | X | Equation | R2 |
|---|---|---|---|---|
| (3) | All Measurable Flocs | Primary Stage Time | Y = 1819.10 + 505.65X | 0.8137 |
| (4) | 2~5 μm Diameter Flocs | Primary Stage Time | Y = 1712.40 + 406.03X | 0.7932 |
| (5) | All Measurable Flocs | Growth Stage End Time | Y = 110.18 + 335.04X | 0.7874 |
| (6) | 2~5 μm Diameter Flocs | Growth Stage End Time | Y = 357.77 + 267.92X | 0.7598 |
| (7) | All Measurable Flocs | Stable Stage Time | Y = 9382.29 − 340.09X | 0.8164 |
| (8) | 2~5 μm Diameter Flocs | Stable Stage Time | Y = 7795.11 − 273.92X | 0.8017 |
| No. | Y | X | Equation | R2 |
|---|---|---|---|---|
| (9) | All Measurable Flocs | D”fP | Y = 457.18X−0.5842 | 0.9092 |
| (10) | 2~5 μm Diameter Flocs | D”fP | Y = 427.16X−0.5620 | 0.9073 |
| (11) | All Measurable Flocs | −D”fG | Y = 302.20X−0.7315 | 0.9189 |
| (12) | 2~5 μm Diameter Flocs | −D”fG | Y = 294.17X−0.6976 | 0.9258 |
| (13) | All Measurable Flocs | WRSS | Y = 9227.65 − 3751.26X | 0.9258 |
| (14) | 2~5 μm Diameter Flocs | WRSS | Y = 7678.76 − 3029.53X | 0.9153 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Li, H. A New Method for the Process Division and Effect Evaluation of Coagulation Based on Particle Size Fractal Dimension. Processes 2018, 6, 237. https://doi.org/10.3390/pr6120237
Zhu Y, Li H. A New Method for the Process Division and Effect Evaluation of Coagulation Based on Particle Size Fractal Dimension. Processes. 2018; 6(12):237. https://doi.org/10.3390/pr6120237
Chicago/Turabian StyleZhu, Yuwen, and Haoyu Li. 2018. "A New Method for the Process Division and Effect Evaluation of Coagulation Based on Particle Size Fractal Dimension" Processes 6, no. 12: 237. https://doi.org/10.3390/pr6120237
APA StyleZhu, Y., & Li, H. (2018). A New Method for the Process Division and Effect Evaluation of Coagulation Based on Particle Size Fractal Dimension. Processes, 6(12), 237. https://doi.org/10.3390/pr6120237