Gaussian Process-Based Hybrid Model for Predicting Oxygen Consumption in the Converter Steelmaking Process

Abstract

Oxygen is one of the most important energies used in converter steelmaking processes of integrated iron and steel works. Precisely forecasting oxygen consumption before processing can benefit process control and energy optimization. This paper assumes there is a linear relationship between the oxygen consumption and input materials, and random noises are caused by other unmeasurable materials and unobserved reactions. Then, a novel hybrid prediction model integrating multiple linear regression (MLR) and Gaussian process regression (GPR) is introduced. In the hybrid model, the MLR method is developed to figure the global trend of the oxygen consumption, and the GPR method is applied to explore the local fluctuation caused by noise. Additionally, to accelerate the computational speed on the practical data set, a K-means clustering method is devised to respectively train a number of GPR models. The proposed hybrid model is validated with the actual data collected from an integrated iron and steel work in China, and compared with benchmark prediction models including MLR, artificial neural network, support vector machine and standard GPR. The forecasting results indicate that the suggested model is able to not only produce satisfactory point forecasts, but also estimate accurate probabilistic intervals.

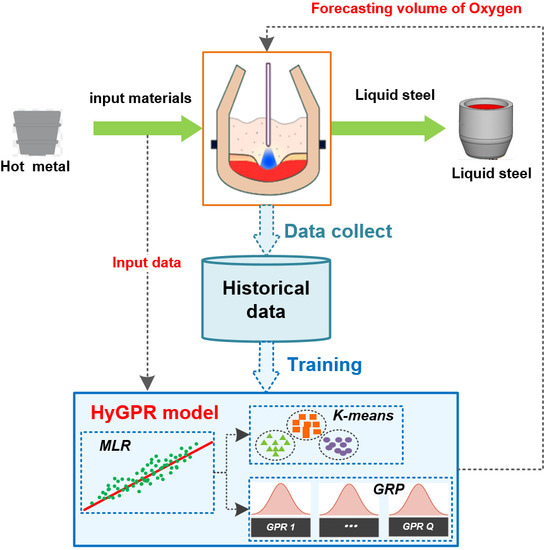
1. Introduction

In modern integrated iron and steel works, oxygen is one of the most important energy resources used in various production processes, such as oxygen-rich combustion for ironmaking, converter blowing for steelmaking, and flame cutting for casting [1]. Statistically, about 20% [2] plant-wide electric power is used to produce the oxygen, and more than 50% [2] oxygen is used in the steelmaking process. To precisely monitor for oxygen consumption not only improves the process controlling performance in the steelmaking process, but also benefits making a satisfactory schedule for oxygen production to achieve the goal of energy saving and economic profits [3].

Traditionally, the main task of the steelmaking process is to produce various grades of steel by removing impurities in hot metal, such as excess carbon, silicon, manganese and phosphorus [4]. The primary steelmaking equipment is called the basic oxygen furnace (BOF) also known as Linz–Donawitz (LD) or oxygen converter (as shown in Figure 1). Theoretically, converter steelmaking is a complex process including melting, purifying, and alloying which are carried out at approximately 1600 °C (2900 °F) in melting conditions. First, the hot metal at 1200–1300 °C, an amount of scrap steel and calcined lime are charged into a converter, which produces violent reactions on the surface of the hot metal and slags. Then, oxygen from a lance is blown onto the liquid metal bath surface within typically 15 min, which continuously increases temperature and reduces the carbon-rich hot metal to low-carbon steel between 0–1.5 percent. The slag-gas emulsion is formed during blowing and will decrease in the later period of blowing. Finally, specified chemical compositions and temperatures are reached by initiating numerous chemical reactions in sequence or simultaneously. In addition, the flux of burnt lime, dolomite and other chemical materials are added to further remove impurities and protect the lining of the converter. In fact, because each reaction couples and interplays with others [5], the process of converter steelmaking is very complex, and the condition of oxygen consumption is hard to be monitored in actual environments. However, with the current trend of Industry 4.0, the industrial process tends to be more expensive, which requires higher system reliability and performance. Therefore, it is needed to find an access to forecast the volume of oxygen consumption, which can boost the control performance of steelmaking process and the operational performance of oxygen distribution to a new level.

With rapid developments of industrial automation and information systems, the industry has established big-data platforms and has collected a vast amount of valuable data [6]. Hence, a considerable number of researchers have used data-driven methodologies to predict these parameters that are hard to directly collect or calculate in the complex process [7,8], such as semiconductor [9], petrochemical [10], and energy process [11]. With concerns on the converter steelmaking process, many efforts have been devoted into predicting the end-point temperature and carbon content [12] in past decades, but the studies on forecasting oxygen consumption have seldom been reported. Since a large number of complex chemical reactions and physical changes in the steelmaking process exist, the exact amount of oxygen required to complete the steelmaking process cannot be calculated directly. Traditionally, these unmeasurable variables were estimated by constructing explicit knowledge models, i.e., material balance, heat balance, kinetics and other theories [13]. However, there are still many unknown factors in the converter steelmaking process, which may cause low precision and unreliability. Therefore, to develop its theoretical model is a high-cost and high-challenge task. However, industrial data produced in the steelmaking process provide a potential way to forecast these unmeasurable variables. These data-driven models complete the prediction task by building the mapping relationship between the input-output data without knowledge about the process. Owing to these advantages, a wide range of data-driven models are applied in the steel industry. Saxén et al. [14] reviewed a variety of prediction models for the silicon content of hot metal produced in blast furnaces. Liu et al. [15] applied a least squares support vector machine (LS-SVM) model to investigate several real-time prediction problems in the converter steelmaking process. Tian and Mao [16] proposed an ensemble extreme learning machine (ELM) to forecast the temperature of liquid steel in the ladle furnace. Han and Liu [17] proposed an ELM with optimized parameters to predict the endpoint carbon content and temperature of liquid steel. Laha et al. [18] compared a number of machine learning models for predicting yield steel in a steelmaking work, and verified that the support vector regression (SVR) is the most powerful one. However, the data-driven model is a black-box lack of interpretation. Therefore, many researchers paid more attention to the hybrid model based on theory and data. Yang et al. [19] developed a hybrid model to predict the electricity demand in the fused magnesia smelting process, in which its mechanism is formulated by a linear model and the unknown factors are modeled by neural networks. Chen et al. [20] proposed a hybrid model combined with a finite element method and an artificial neural network (ANN) to predict the degree of void closure produced in the cold rolling process. Lei and Su [21] developed an SVR-based hybrid model to forecast the mold level of the continuous casting production process.

The remaining sections of the paper are organized as follows. Section 2 provides the details of the proposed Gaussian process-based hybrid model named HyGPR. The experimental setup and results are analyzed and discussed in Section 3. Finally, Section 4 draws conclusions of this study and identifies several topics for future studies.

2. Methodology

The consumed volume of oxygen during the converter steelmaking process is mainly related with the following four types of factors:

(1)

The amount of input materials, such as the carbon, silicon, manganese, phosphorus, sulfur content of hot metal.

(2)

The control parameters of blowing, e.g., lance position, and blowing pattern.

(3)

The final smelting targets, e.g., oxygen consumption highly depends on the carbon target.

(4)

The equipment conditions, e.g., converter lining and internal converter geometry.

In this study, the exact amount of oxygen that will be consumed in the not-started steelmaking process is forecasted. This task is usually realized by static prediction models (before blowing) which obviously differ with dynamic prediction models (during blowing). Hence, the control parameters are not selected in this study. Since the final carbon target of the similar steel grades is very close, prediction models can be trained independently with different carbon target. The equipment conditions cannot be directly observed, so we assume they are constants within a short period. Therefore, only the input materials are considered in our proposed methodology stated in the following subsections.

2.1. Reaction-Based Linear Model

To describe the converter steelmaking process, reaction Equations (1)–(9) are defined where the symbols $[·]$, $(·)$ and $\{·\}$ indicate metal, slag and gas phases, respectively. As shown in (1)–(6) oxidation is the most important chemical reaction mainly carried out on the hot metal, which converts carbon to carbon oxide, silicon to silica, manganese to manganous oxide, phosphorus to phosphate, and sulphur to sulfur dioxide.

$$\left[C\right]+\frac{1}{2}\left\{O_2\right\}=\left\{CO\right\}$$

(1)

$$\left[C\right]+\left\{O_2\right\}=\left\{C{O}_2\right\}$$

(2)

$$\left[Si\right]+\left\{O_2\right\}=\left(Si{O}_2\right)$$

(3)

$$\left[Mn\right]+\frac{1}{2}\left\{O_2\right\}=\left(MnO\right)$$

(4)

$$2\left[P\right]+\frac{5}{2}\left\{O_2\right\}=\left(P_2{O}_5\right)$$

(5)

$$\left[S\right]+\left\{O_2\right\}=\left\{S{O}_2\right\}$$

(6)

Unfortunately, a little iron is also combined with oxygen in addition to these chemical reactions, and produces $F{e}_x{O}_y$ as follows.

$$2\left[Fe\right]+\frac{3}{2}\left\{O_2\right\}=\left(F{e}_2{O}_3\right)$$

(7)

$$\left[Fe\right]+\frac{1}{2}\left\{O_2\right\}=\left(FeO\right)$$

(8)

In addition, the liquid slag releases a little oxygen, and acts as an oxidizer to produce some by-products:

$$\left[S\right]+\left(CaO\right)\to \left(CaS\right)+\left[O\right]$$

(9)

It should be noted that, a number of other oxygen-related reactions occur in the steelmaking process. For instance, the post reaction $\left\{CO\right\}+\frac{1}{2}\left\{O_2\right\}\to \left\{C{O}_2\right\}$ will consume an amount of oxygen, and the $C$ element in the converter lining will also absorb oxygen. Specially, when the phenomenon of rephosphoration and remanganization occur with rising temperatures and low $FeO$ contents in the slag, the reduction of the $\left(P_2{O}_5\right)$ and $\left(MnO\right)$ with the solved $\left[C\right]$ in the steel droplets in the slag/gas emulsion will release a little oxygen. However, these reactions fail to be directly observed and recorded. Therefore, the consumed and released oxygen during the reaction or blowing are identified as constants or random noises.

We classify these input materials ($\mathit{x}$) into two sets: The materials consumed oxygen ${\mathit{O}}^{+}$ and the materials released oxygen ${\mathit{O}}^{-}$. To estimate the value of oxygen consumption ($y$), we assume there is linear relationship between $\mathit{x}$ and:

$$y=f\left(\mathit{x}\right)={\displaystyle \sum }_{i=1}^{m_1}{w}_i{x}_i+{\displaystyle \sum }_{i=1}^{m_2}{w}_i\left(-x_i\right)+w_0={\displaystyle \sum }_{i=1}^{m_1}{w}_i{x}_i-{\displaystyle \sum }_{i=1}^{m_2}{w}_i{x}_i+w_0$$

(10)

where $\mathit{x}=\left(x_1,\cdots ,x_m\right)$ represents the materials reacting with oxygen, $w_i$ denotes their reactions coefficient, $w_0$ is a constant term determined by learning from data, $m_1$ and $m_2$ respectively represent the size of $O^{+}$ and $O^{-}$, and $m_1+m_2=m$. To determine the values of $w=\left(w_0,w_1,\cdots ,w_m\right)$, the pre-defined loss function Equation (11) is minimized.

$$J\left(w\right)=\frac{1}{2m}{\displaystyle \sum }_{j=1}^m\left(f\left({\mathit{x}}^{\left(j\right)}\right)-y^{\left(j\right)}\right)$$

(11)

where ${\mathit{x}}^{\left(j\right)}$ and $y^{\left(j\right)}$ respectively represent the input and output values of $j^{th}$ sample data. The loss function $J\left(w\right)$ can be solved by the least square or gradient descent least angle method [22].

However, the suggested multiple linear regression (MLR) model is an ideal theoretical model, because the converter steelmaking process in nature is a complex system with multi-component, multi-phase and multi-reaction, the detailed process of each reaction is impossible to be precisely formulated. Additionally, in actual production environments, considerable number factors played in or affected the reactions fail to be observed. Therefore, the MLR model based on these reactions always suffers from low precision and low robustness in the actual production process. To overcome this shortage, this study develops the data-driven prediction model in Section 2.2.

2.2. Gaussian Process Regression with Noise

Gaussian process regression (GPR) [23] is a non-parametric prediction model based on the Gaussian prior distribution. The two main advantages of GPR are the interpretability between the prediction and observations, and the probabilistic sense when some prior models are embedded. In the past decades, theoretical research and real-world application have proved that GPR is a powerful tool for supervised learning applications [24]. Given a dataset $\mathcal{D}=\left\{\mathit{X},\mathit{y}\right\}$, where $\mathit{X}\in {ℝ}^{n\times m}$, $\mathit{y}\in {ℝ}^{n\times 1}$, $n$ is the sample size, and $m$ is the sample dimension. Assume the regression function $f$ mapping an input vector $\mathit{x}$ to an output value $y$ can be written as:

$$y=f\left(\mathit{x}\right)+ϵ$$

(12)

where noise $ϵ$ is the noise with Gaussian distribution $\mathcal{N}\left(0,{\sigma }_n^2\right)$ and the “signal” term $f\left(\mathit{x}\right)$ and noise $ϵ$ are mutually independent. The signal term $f\left(\mathit{x}\right)$ is also assumed to be a random variable with Gaussian distribution.

$$f\left(\mathit{x}\right)~\mathcal{G}\mathcal{P}\left(m\left(\mathit{x}\right),k\left(\mathit{x},{\mathit{x}}^{\prime }\right)\right)$$

(13)

where $m\left(\mathit{x}\right)=E\left(f\left(\mathit{x}\right)\right)$ is a mean function which often set to 0, and $k\left(\mathit{x},{\mathit{x}}^{\prime }\right)=E\left[\left(f\left(\mathit{x}\right)-m\left(\mathit{x}\right)\right)\left(f\left({\mathit{x}}^{\prime }\right)-m\left({\mathit{x}}^{\prime }\right)\right)\right]$ is a covariance that illustrates prior assumptions including likely smoothness and patterns in the data. The covariance function $k$ is also identified as the kernel function of Gaussian process [25].

Given a collected data set $\mathcal{D}=\left\{\mathit{X},\mathit{y}\right\}$, a predicted signal function $f_{\ast }$ should be constructed in order to forecast a new output $y^{\ast }$ based on a new input ${\mathit{x}}^{\ast }$. Once we have determined the mean function and the kernel, the predicted function $f_{\ast }$ can be sampled as follows.

$$f_{\ast }~\mathcal{N}\left(\mathbf{0},\mathit{k}\left({\mathit{x}}^{\ast },\mathit{x}\right)\right)$$

(14)

Then, the joint probabilistic distribution of the training outputs $\mathit{y}$ and the predicted function $f_{\ast }$ can be written as:

$$\left[\begin{array}{c}\mathit{y}\\ f_{\ast }\end{array}\right]=\mathcal{N}\left(0,\left[\begin{array}{cc}K\left(\mathit{X},\mathit{X}\right)+{\sigma }_n^2{\mathit{I}}_n& K\left(\mathit{X},x_{\ast }\right)\\ \mathit{K}\left(x_{\ast },X\right)& k\left(x_{\ast },x_{\ast }\right)\end{array}\right]\right)$$

(15)

where $K\left(X,X\right)$ denotes the covariance matrix between all training inputs, $K\left(\mathit{X},x_{\ast }\right)$ represents the covariance matrix between the training inputs and test inputs, $\mathit{K}\left(x_{\ast },X\right)$ stands for the covariance matrix between the test inputs and training inputs, $k\left(x_{\ast },x_{\ast }\right)$ is the covariance between test inputs. ${\mathit{I}}_n$ is an identity matrix and ${\sigma }_n^2$ is the assumed variance of training samples.

The main task of GPR is to forecast the most likely value of $y^{\ast }$ related to $x^{\ast }$. Based on the Bayes’ principle, the conditional distribution is concluded [23] as:

$$p\left(\left(f_{\ast }|{\mathit{x}}_{\ast },X,y\right)\right)~\mathcal{N}\left(m_{\ast },Cov\left(f_{\ast }\right)\right)$$

(16)

$$m_{\ast }=K\left({\mathit{x}}_{\ast },\mathit{X}\right){\left[K\left(\mathit{X},\mathit{X}\right)+{\sigma }_n^2{\mathit{I}}_n\right]}^{-1}\mathit{y}$$

(17)

$$Cov\left({\mathit{f}}_{\ast }\right)=k\left({\mathit{x}}_{\ast },{\mathit{x}}_{\ast }\right)-K\left({\mathit{x}}_{\ast },\mathit{X}\right){\left[K\left(\mathit{X},\mathit{X}\right)+{\sigma }_n^2{\mathit{I}}_n\right]}^{-1}K\left({\mathit{x}}_{\ast },\mathit{X}\right)$$

(18)

Based on these theoretical analysis, the mean and covariance function are the two most important elements in GPR. The kernel function $\mathit{k}$ directly illustrates prior knowledge about the function $f$, and the combinations between two different kernel functions still can be identified as a kernel [25]. In this paper, we use a composite covariance function with the squared exponential kernel function $k_1\left(\mathit{x},{\mathit{x}}^{\prime }\right)$ Equation (19) to express smooth trend of the data and the exponential kernel functions $k_2\left(\mathit{x},{\mathit{x}}^{\prime }\right)$ Equation (20) to illustrate the irregularity of the data.

$$k_1\left(\mathit{x},{\mathit{x}}^{\prime }\right)={\sigma }_{f_1}^{2}exp\left(-\frac{1}{2}{\left(\mathit{x}-{\mathit{x}}^{\prime }\right)}^T{\left[\begin{array}{ccc}{l}_{s1}^2& & \\ & \ddots & \\ & & l_{sp}^2\end{array}\right]}^{-1}\left(x-x^{\prime }\right)\right)$$

(19)

$$k_2\left(\mathit{x},{\mathit{x}}^{\prime }\right)={\sigma }_{f_2}^{2}exp\left(-\sqrt{\left(\mathit{x}-{\mathit{x}}^{\prime }\right){\left[\begin{array}{ccc}{l}_{e1}^2& & \\ & \ddots & \\ & & l_{ep}^2\end{array}\right]}^{-1}\left(x-x^{\prime }\right)}\right)$$

(20)

$$k\left(\mathit{x},{\mathit{x}}^{\prime }\right)=k_1\left(\mathit{x},{\mathit{x}}^{\prime }\right)+k_2\left(\mathit{x},{\mathit{x}}^{\prime }\right)$$

(21)

2.3. HyGPR with K-Means Clustering

In this study, the novel hybrid model HyGPR integrating the parametric MLR model and the non-parametric GPR model are constructed to forecast the oxygen consumption in the converter steelmaking process.

$$f\left(\mathit{x}\right)={\mathit{w}}^T\mathit{x}+g\left(\mathit{x}\right)$$

(22)

where ${\mathit{w}}^{\mathit{T}}$ is the weight vector of the MLR model defined in Equation (10) and $g\left(\mathit{x}\right)~\mathcal{G}\mathcal{P}\left(0,k\left(\mathit{x},{\mathit{x}}^{\prime }\right)\right)$.

Such a hybrid model can bridge the gap between the interpretability of the parametric model MLR and the accuracy of non-parametric model GPR, where MLR is identified as the prior model. Note that the proposed hybrid model can be identified as a special GPR, where the mean function is defined as a linear function and the covariance function is formed as a composite kernel function defined in Equations (19)–(21).

The hyper-parameters of the proposed hybrid model are formed as a vector $\theta =\left\{w_0,w_1,\dots ,w_m, {\sigma }_{f_1}^2,l_{s1}^2,\dots ,l_{sm}^2,l_{e1}^2,\dots ,l_{em}^2\right\}$. To seek the optimal hyper-parameters, we need to maximize the log marginal likelihood [23].

$$\log p\left(\mathit{y}|\theta \right)=-\frac{1}{2}{\left(\mathit{y}-\mathit{m}\right)}^T{K}^{-1}\left(\mathit{y}-\mathit{m}\right)-\frac{1}{2}\log \left|K\right|-\frac{n}{2}\log 2\pi$$

(23)

where $\mathit{m}={\mathit{w}}^{\mathit{T}}\mathit{X}$, and $K_{ij}=k\left(x_i,x_j\right)$. When solving this equation, the most challengeable and time-consuming task is finding the inverse matrix $K^{-1}$ with high dimensions.

To apply the proposed HyGPR model in an actual environment, we employ a K-means clustering method to reduce the training sample size (as shown in Figure 2). When training the noise function $g\left(x\right)$, we use the K-means clustering method with the same input variables as MLR and GPR to decompose the training set $\mathcal{D}=\left\{\mathit{X},\mathit{y}\right\}$ into $Q$ subsets, and respectively train $Q$ GPR models. When a new input ${\mathit{x}}^{\prime }$ arrives, the HyGPR firstly forecasts the value of $f\left({\mathit{x}}^{\prime }\right)$ using the MLR model, and then predicts the value of $g\left({\mathit{x}}^{\prime }\right)$ using the $q^{th}$ GPR model selected by the K-means clustering model. With this decomposition manner, the training speed of the GPR is assumed to be accelerated because the dimension of the observed matrix is reduced.

3. Experiments and Discussion

3.1. Data Set

To test the proposed HyGPR model, we collected the real-world process data of the converter steelmaking process in an integrated iron and steel works situated in the north of China. The data set has 1534 observed samples between 1 April 2018 and 30 June 2018. Figure 3 indicates the distribution of the observed outputs, which is irregular and fluctuates severely. The selected input variables includes:

(1)

The weight of hot metal (Fe).

(2)

The weight of impurity elements, e.g., carbon (C), silicon (Si), manganese (Mn), sulphur (S) and phosphorus (S) which are the products of the weights of hot metal and the element percentages.

(3)

Five additional materials (AM) for steelmaking, of which the real compositions are secreted.

The statistics information such as means, standard deviations, minimum and maximum values, are summarized in

Table 1. Descriptive statistics of data set.

Parameters	Mean.	Std.	Minimum	Maximum
Fe (t)	276.8450	252.7000	289.8000	21.6711
C (t)	12.1259	0.5061	10.3288	14.0078
Si (t)	0.9477	0.4456	0.0318	2.332
Mn (t)	0.4332	0.2047	0.1252	2.2066
P (t)	0.2431	0.0221	0.1736	0.4119
S (t)	0.0023	0.0022	0	0.0343
AM1 (t)	1.7980	1.4659	0	9.908
AM2 (t)	1.7487	1.6683	0	8.172
AM3 (t)	14.1139	2.5374	5.9610	28.937
AM4 (t)	4.1623	1.3636	0	9.66
AM5 (t)	0.7833	1.6976	0	11.994
O2 (103m3)	13.7823	0.8079	11.0480	15.913

. To evaluate the performance of the proposed model, we divided the dataset into two sets with the handout way: The former 1381 samples (about 90%) for learning HyGPR and second 153 samples (10%) for testing.

3.2. Evaluation Metrics

In order to compare HyGPR with the other benchmark prediction model, we defined four metrics to assess quantitatively its point and interval forecasting ability. There accuracy metrics for the point prediction including root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) were formulated in Equations (24)–(26).

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left(y_i-{\widehat{y}}_i\right)}^2}{N}}$$

(24)

$$\mathrm{MAE}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\left|y_i-{\widehat{y}}_i\right|$$

(25)

$$\mathrm{MAPE}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\times 100\%$$

(26)

where $y_i$ and ${\widehat{y}}_i$ denote respectively the observed and predicted oxygen consumption in the $i^{th}$ test sample; $N$ is the size of the test sample. Note that the small values of these metrics indicate high prediction accuracy.

The proposed HyGPR model is able to provide not only the forecasting point ${\widehat{y}}_i$ but also the confidence interval $\left[{\widehat{y}}_i^{-},{\widehat{y}}_i^{+}\right]$ of future oxygen consumption. Therefore, we defined a coverage metric for interval prediction named hit ratio (HRI) in Equation (27) which is applied to calculate the number of test samples fallen into the 95% confidence interval.

$$\mathrm{HRI}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{I}_A\left({\widehat{y}}_i\right)\times 100\%$$

(27)

where $A=\left\{{\widehat{y}}_i|{\widehat{y}}_i^{-}\le {\widehat{y}}_i\le {\widehat{y}}_i^{+}\right\}$, and $I_A\left({\widehat{y}}_i\right)=\{\begin{array}{c}1, {\widehat{y}}_i\in A\\ 0, {\widehat{y}}_i\notin A\end{array}$.

Additionally, we also used the CPU running time (seconds) to evaluate the learning speed of the tested models.

3.3. Results and Analysis

In this study, all proposed and benchmark models are implemented with the MATLAB 2017 software. Especially, we used the GPML (Gaussian processes for machine learning) toolbox [26] to construct the GPR model and the one in HyGPR, and other compared models were provided by the toolboxes installed in MATLAB. All programs ran on a personal computer with an Intel Core i7-8550U Processor (1.8550GHz) and 16.0GB Memory and installing a Windows 10 operating system.

In the proposed HyGPR model, the cluster count ($Q$) of K-means is a very important factor that may influence the final prediction performance. To select the most appropriate value of $Q$, we carried out five group experiments with different clusters. The results of the four accuracy metrics were listed in

Table 2. Experimental results for candidate clusters (The best metrics are highlighted in bold).

Cluster Count	RMSE (103m3)	MAE (103m3)	MAPE (%)	CPU Time (S)
Q = 1	0.64	0.49	3.56	62.47
Q = 2	0.64	0.48	3.51	27.62
Q = 3	0.63	0.49	3.55	19.82
Q = 4	0.63	0.48	3.52	13.32
Q = 5	0.64	0.53	3.90	15.49

and the forecasting plots were shown in Figure 4.

According to results listed in Table 2, we found that the RMSE, MAE and MAPE of the HyGPR model with different clusters were approximate, but the CPU time was reduced greatly when $Q>1$. Since the HyGPR with four clusters could run successfully within the shortest time, we set $Q=4$ in following computational experiments. In addition, we also found that most of the actual data located in the 95% confidence interval was provided by HyGPR, which means the proposed model was able to make a probabilistic sense.

In order to further evaluate the prediction accuracy of the HyGPR model, we compared it with three benchmark models including MLR, ANN [27], and the support vector machine (SVM) [28]. The MLR model was created by the function fitlm in MATLAB. The function fitnet in MATLAB was adopted to construct ANN with three layers and 10 nodes in the hidden layer, in which the network parameters were optimized by the Levenberg–Marquardt method. The function fitrsvm in MATLAB was used to construct the SVM model with the radial basis function (RBF) kernel, in which the hyperparameters were automatically optimized by minimizing the five-fold cross-validation loss function.

To quantitatively select the best one from the testing models, the computational results of the point evaluation metrics were listed in

Table 3. Performance evaluation of compared models on the test set (The best metrics are highlighted in bold).

Model	RMSE (103m3)	MAE (103m3)	MAPE (%)
MLR	0.70	0.54	3.95
SVM	0.69	0.53	3.92
ANN	0.68	0.52	3.84
HyGPR	0.63	0.48	3.52

. It can be observed that the proposed HyGPR model obtained the smallest of RMSE, MAE and MAPE, while the proposed MLR got the worst results of RMSE, MAE and MAPE. The above results focused on the prediction accuracy of the single valued point predictions (as shown in Figure 5).

Usually, the MLR, ANN and SVM can only provide point estimations of future oxygen consumption. However, the HyGPR model can provide not only the forecasting point ${\widehat{y}}_i$ but also the confidence interval $\left[{\widehat{y}}_i^{-},{\widehat{y}}_i^{+}\right]$ of future oxygen consumption. To test its HRI within 95% confidence interval of HyGPR, we compared it with the standard GPR with the squared exponential kernel function.

Table 4. Accuracy and interval metrics of GPR and HyGPR (The best metrics are highlighted in bold).

Model	RMSE (103m3)	MAE (103m3)	MAPE (%)	HRI (%)	CPU (S)
GPR	0.63	0.49	3.59	92.42%	75.74
HyGPR	0.63	0.48	3.52	96.08%	14.14

listed the evaluation results of GPR and HyGPR. The HyGPR obtained the same value of RMSE and slightly better value of MAE, MAPE and HRI, but its computing speed is more than five times as fast as the standard GPR. Figure 6 showed the point forecasts and the corresponding 95% confidence intervals. It can also be observed that nearly all of the actual observations fell in the confidence intervals.

4. Conclusions

With the increased concerns on the management and optimization of energy systems, it is necessary for modern integrated iron and steel works to develop an accurate and robust model to forecast oxygen consumption. However, it is challengeable to directly forecast oxygen consumption with a simple regression model due to its intermittent and uncertain features. In this study, we introduce a novel hybrid model named HyGPR integrating MLR and GPR. In the proposed prediction model, the MLR model is developed to figure the global trend of the oxygen consumption, and the GPR is applied to explore the local fluctuation caused by noise. Additionally, to overcome the shortcoming of GPR on training speed, a K-means clustering method is applied to decompose the training dataset into a number of subsets. The effectiveness of the HyGPR was verified using the actual process data collected from a large integrated iron and steel works located in the north of China. Afterwards, HyGPR is compared with MLR, ANN, SVM and GPR. The results show that HyGPR can obtain the best point prediction metrics in terms of RMSE, MAE, and MAPE, and the better interval prediction performance in terms of HRI. Furthermore, it runs more than five times faster than the standard GPR. Therefore, it can be concluded that the proposed method is an effective tool to improve the forecasting accuracy and coverage. Moreover, HyGPR runs faster than the standard GPR model due to implementing the decomposition policy.

In future studies, we will investigate the following issues that may be meaningful for industrial application and scientific research:

(1).

The online prediction model involving dynamic operating parameters, such as the position of oxygen lance, the pressure of oxygen blowing and the duration of oxygen blowing.

(2).

The prediction model to forecast slopping events, which is very important to reduce production costs and environmental impacts.

(3).

In this study, we assume that the noise of the steelmaking process is a Gaussian distribution. However, when it comes to the small-sample and high-dimensional data set, the assumption is incorrect. So it needs to develop a non-Gaussian prediction model applied in other environments.