3-D Modeling of Dehydration Kinetics and Shrinkage of Ellipsoidal Fermented Amazonian Cocoa Beans

Abstract

A recently proposed moving-boundary model for food isothermal dehydration was applied to analyze the dehydration kinetics of ellipsoidal cocoa beans, characterized by a moderate shrinkage and a non-uniform initial distribution of water content between the core and the shell of the bean. The aim is to predict the influence of air velocity and non-uniformity of the initial water distribution on the dehydration rates, as well as the temporal evolution of the water content in the core and in the shell and of the characteristic lengths of the ellipsoidal bean. The model proved capable of accurately describing the two-phases dehydration process: an initial fast dehydration of the shell, characterized by higher dehydration rates, followed by a slower dehydration of the core, characterized by a linear relationship $j_d=\delta \left(T\right)X_r$ between the dehydration rate $j_d$ and the moisture ratio $X_r$. A shortcut method to estimate the effective water diffusivity D is also proposed, deriving from the basic observation that the asymptotic exponential behaviour of the dehydration curve $X_r\left(t\right)$ for an ellipsoidal bean coincides with that of an equivalent sphere, with the same surface-to-volume ratio.

1. Introduction

The cocoa beans extracted from the fruit of the cocoa tree (Theobroma cacao, see Figure 1) are the raw material for chocolate production [1]. Cocoa beans are usually subjected to fermentation and drying [2,3,4,5,6]. The principal aim of drying is to reduce the moisture content, the main culprit of bean spoilage due to bacteria, yeast, and mould growth. The drying operation can be provided by two methods: natural drying [7], when cocoa beans are spread on a support and exposed directly to sun, or artificial convective drying [3], in which cocoa beans are placed in a dryer and exposed to an air flow with controlled velocity, temperature and humidity. The main drawbacks of natural drying are connected to weather unpredictability which could cause prolonged drying duration and products’ spoilage whereas the advantages of artificial drying are paid with high energy and plant costs [5,6].

The cocoa fruit are usually ellipsoidal in shape and the internal structure consists of a central core surrounded by a thin shell [8], representing about 20% of the total mass of the bean [9,10]. The water content in the core and the shell can be very different and this may have a strong influence on the dehydration kinetics that is accompanied by a moderate volume reduction (shrinkage), about 30% of the initial volume.

Mathematical modeling of cocoa bean’s drying kinetics can be a useful tool to identify the best operative conditions, in the case of artificial drying, or to estimate the optimal drying time, in the case of natural drying.

Few attempts were made, in the recent literature, to model the dehydration kinetics of cocoa beans in all its complexity related to the ellipsoidal shape of the bean (intrinsic 3-d problem [6,11]), to the volume shrinkage [12] and to the necessity to account for mass transfer resistance at the solid/air interface [6,11].

The general objective of this work is to apply the moving-boundary model for food isothermal dehydration, recently proposed by Adrover et al. [13,14], to analyze and characterize the dehydration kinetics and shrinkage of cocoa beans, starting from the experimental data reported by Herman et al. [9,10] who have recently published the results of an extensive experimental campaign on fermented Amazonian cocoa beans. In [9,10], Herman et al. investigate the temporal evolution, during convective drying, of the water content in the core and the shell of fermented Amazonian cocoa beans, in order to better characterize the drying kinetics and to investigate the influence of operating parameters, namely the air velocity and the drying temperature.

The moving-boundary model by Adrover et al. [13,14] was already successfully applied to describe the dehydration kinetics and shrinkage of different food materials and different sample shapes, e.g., eggplant cylindrical [14] and discoidal samples [15], chajote slices [16], potatoes sticks [14] and square slices [13].

In this work, the moving-boundary model is applied to 3-d ellipsoidal beans, accounting for the specific internal structure of the bean (core and shell), the non-uniformity of the initial water content and the volume shrinkage in order to better understand and to accurately describe the two-phases dehydration process of cocoa beans, as observed by Herman et al. [9,10]: an initial fast dehydration of the shell, characterized by higher dehydration rates, followed by a slower dehydration of the core, characterized by a linear relationship between the dehydration rate $j_d$ and the moisture ratio $X_r$.

The article is organized as follows. In Section 2, a review of the morphological and physical parameters of fermented Amazonian cocoa beans is presented, thus highlighting the differences, in the initial distribution of the moisture content and in the final shrinkage, between two different sets of cocoa beans whose dehydration kinetics will be analyzed.

In Section 3, the basic equations for the isothermal moving-boundary model are presented and subsequently applied to ellipsoidal beans in order to investigate: (i) the influence of the ellipsoidal shape on dehydration kinetics in the simplest case of a uniform initial water distribution; (ii) the influence of a nonuniform initial water distribution on dehydration rates, in the absence of shrinkage; (iii) the influence, on dehydration rates, of a constant shrinkage factor.

Section 4 is devoted to modeling the dehydration kinetics and shrinkage of Amazonian cocoa beans, thus obtaining: (i) a reliable estimate of the effective water diffusivity at different temperatures; (ii) an accurate prediction of the influence of air velocity and non-uniformity of the initial water distribution on dehydration kinetics; (iii) a correct description of the temporal evolution of the moisture content and thickness of core and shell.

2. Morphological and Physical Characterization of Ellipsoidal Cocoa Beans

We analyze experimental data of hot-air drying of fermented Amazonian cocoa beans (data from Herman et al. [9,10]) in a convective dryer at different temperatures $T=30,40,50,60$${}^{\circ }$C and different air velocities $v=0.3,0.6,1$ m/s. Fermented Amazonian cocoa beans were fermented at 30 ${}^{\circ }$C for seven days in wooden boxes and stored at $-18$${}^{\circ }$C until drying. Two different sets of data are analyzed and compared. Data set (1) from [9] and data set (2) from [10] both refer to fermented Amazonian beans (Theobroma cacao, var. Forasteiro) from Quatro-Bocas, State of Pará, Brasil, with ellipsoidal shape (see Figure 2).

The main morphological and physical parameters, namely the initial length of the three principal axes $a_0$, $b_0$, $c_0$, the initial shell thickness ${\lambda }_0$, the initial total moisture content $X_0$ and the initial moisture content of the core $X_0^{core}$, are reported in

Table 1. Morphological and physical parameters of two different sets of freshly fermented Amazonian cocoa beans. Data set (1) are reported in [9]. Data set (2) are reported in [10].

Data	${\mathit{a}}_0$	${\mathit{b}}_0$	${\mathit{c}}_0$	${\mathit{\lambda }}_0$	${\mathit{X}}_0$	${\mathit{X}}_0^{\mathbf{core}}$	${\mathit{X}}_0^{\mathbf{core}}/{\mathit{X}}_0$	${\mathit{V}}_0^{\mathbf{core}}/{\mathit{V}}_0$
Set	(mm)	(mm)	(mm)	(mm)	(kg/kg db)	(kg/kg db)	(-)	(-)
(1)	24.7 ± 0.72	12.73 ± 0.5	8.94 ± 0.86	0.45 ± 0.09	0.82 ± 0.09	0.6 ± 0.08	≃ 0.73	≃ 0.8
(2)	24.28 ± 1.57	13.34 ± 0.5	8.52 ± 0.35	0.58 ± 0.09	≃ 0.88	≃ 0.49	≃ 0.56	≃ 0.72

.

Specifically, the initial moisture content of the core $X_0^{core}$ was experimentally evaluated by peeling the fresh shell and then drying separately the core and the shell for 24 h at 105 ${}^{\circ }$C, thus evaluating $X_0^{core}$ as

$$X_0^{core}=\frac{M_0^{core}-M_d^{core}}{M_d^{core}+M_d^{shell}}$$

(1)

where $M_0^{core}$ is the mass of the fresh core, $M_d^{core}$ and $M_d^{shell}$ are the mass of the dry core and of the dry shell, respectively. For a detailed discussion about the experimental procedure see [9].

From the initial mass $M_0\simeq 1.87\pm 0.24$ g and the initial moisture content $X_0$, the initial volume fraction ${\varphi }_0$ (averaged over the entire bean, i.e., core and shell) of water inside the cocoa bean, before drying, can been estimated as follows

$${\varphi }_0=\frac{M_0-M_d}{{\rho }_w{V}_0}=\frac{M_0}{{\rho }_w{V}_0}\frac{X_0}{1+X_0}$$

(2)

where $M_d=M_d^{core}+M_d^{shell}$ is the total dry mass and ${\rho }_w$ is the water density, thus obtaining ${\varphi }_0\simeq 0.57$ for data set (1) and ${\varphi }_0=0.59$ for data set (2).

The volume fraction of water in the core ${\varphi }_0^{core}$ and in the shell ${\varphi }_0^{shell}$ can been evaluated, from the material balance

$${\varphi }_0{V}_0={\varphi }_0^{core}{V}_0^{core}+{\varphi }_0^{shell}{V}_0^{shell}$$

(3)

as follows

$${\varphi }_0^{core}={\varphi }_0\underset{{\beta }_0^{core}}{\underbrace{\frac{X_0^{core}/X_0}{V_0^{core}/V_0}}},{\varphi }_0^{shell}={\varphi }_0\underset{{\beta }_0^{shell}}{\underbrace{\frac{1-X_0^{core}/X_0}{1-V_0^{core}/V_0}}}$$

(4)

From the morphological and physical parameters reported in Table 1, it can be observed that the two sets of cocoa beans differ significantly in the ratio $X_0^{core}/X_0$ and this implies very different values for the partition factors ${\beta }_0^{core}$ and ${\beta }_0^{shell}$, namely ${\beta }_0^{core}\simeq 0.912$ and ${\beta }_0^{shell}\simeq 1.35$ for data set (1) and ${\beta }_0^{core}\simeq 0.78$ and ${\beta }_0^{shell}\simeq 1.53$ for data set (2). The higher the value of water concentration in the shell, the faster the decrease of the total moisture content at the beginning of the drying process, and therefore the larger the initial dehydration rate.

Focusing on volume shrinkage, the sample volume $V_d$ after complete drying, can be estimated from data reported in [9,10]. In [9], Herman et al. evaluated the volume $V_0=(\pi /6)a_0{b}_0{c}_0$ of the fresh bean as well as the volume of the dry bean $V_d=(\pi /6)a_d{b}_d{c}_d$, where $a_d,b_d,c_d$ represent the lengths of the principal axes of the bean after drying. These authors approximate the ellipsoidal shape of the bean with a cylinder of height $H=a$ and radius $R=\sqrt{bc/6}$, i.e., a cylinder with the same volume as the ellipsoid and height H equal to the length a of the main principal axes of the ellipsoid. As a consequence, they report the morphological parameters of the fresh bean as $a_0=25.5$ mm, $R_0=4.5$ mm and the shrinkage parameters as $a_d/a_0=0.93\pm 0.09$ and $R_d/R_0=0.94\pm 0.019$, $a_d$ and $R_d$ being the height and the radius of the equivalent cylinder, after drying. From these data, it is possible to estimate the rescaled dry-sample volume $V_d/V_0$ as

$$\frac{V_d}{V_0}=\frac{\pi a_0{R}_0^2}{\pi a_d{R}_d^2}=\left(\frac{a_d}{a_0}\right){\left(\frac{R_d}{R_0}\right)}^2\simeq 0.82$$

(5)

The rescaled dry-sample volume $V_d/V_0\simeq 0.82$ obtained from data set (1) [9] is in agreement with that obtained from data set (2) [10]. In [10], the authors report the three ratios $a_d/a_0\simeq 0.88$, $b_d/b_0\simeq 0.94$ and $c_d/c_0\simeq 0.94$ for the principal axes of the ellipse, so that the rescaled dry-sample volume $V_d/V_0$ can be directly evaluated as

$$\frac{V_d}{V_0}=\left(\frac{a_d}{a_0}\right)\left(\frac{b_d}{b_0}\right)\left(\frac{c_d}{c_0}\right)\simeq 0.78$$

(6)

This slightly larger shrinkage is reasonably due to the higher initial moisture content $X_0$.

These experimental findings are also in agreement with shrinkage data reported by Koua et al. [7] for indirect solar drying of cocoa beans from Cote d’Ivore. Ellipsoidal cocoa beans used by Koua et al. are bigger than Amazonian cocoa beans used by Herman et al. Indeed, the lengths of the three principal axes are $a_0=27.6$ mm, $b_0=15.5$ mm and $c_0=11.3$ mm and also the initial moisture content $X_0=1.22$ (kg/kg db) is larger than that for Amazonian cocoa beans. Koua et al. experimentally observed a linear relationship between the rescaled volume $V/V_0$ and the moisture content reduction $X/X_0$ during the drying process, approximated as

$$\frac{V\left(t\right)}{V_0}=1-0.276\left(X_0-X\left(t\right)\right).$$

(7)

After complete drying, the final moisture content $X_d=0.076$ was evaluated and the resulting rescaled dry-sample volume attains the value $V_d/V_0\simeq 0.68$. The larger shrinkage, also in this case, may be due to a significantly higher initial moisture content $X_0$.

The equilibrium water volume fraction ${\varphi }_{eq}$ can be evaluated, from the equilibrium $X_{eq}$ and initial $X_0$ moisture contents and the rescaled dry-sample volume $V_d/V_0$, as follows

$${\varphi }_{eq}={\varphi }_0\left(\frac{X_{eq}}{X_0}\right){\left(\frac{V_d}{V_0}\right)}^{-1}$$

(8)

where the sample volume at equilibrium $V_{eq}$ was approximated with the dry-sample volume $V_d$. For both data sets (1) and (2), the rescaled equilibrium moisture content $X_{eq}/X_0$ is assumed $X_{eq}/X_0=0.055$ (kg/ kg db) in agreement with the asymptotic value of the rescaled moisture content derived from dehydration curves of cocoa beans reported in [9,10] analyzed in Section 4.1 and Section 4.2. The resulting values are ${\varphi }_{eq}\simeq 0.038$ for data set (1) and ${\varphi }_{eq}\simeq 0.041$ for data set (2).

All these physical and morphological parameters $a_0,b_0,c_0,{\lambda }_0$, $V_0^{core}/V_0$, $V_0^{shell}/V_0$, $V_d/V_0$, ${\varphi }_0$, ${\varphi }_0^{core}$, ${\varphi }_0^{shell}$ and ${\varphi }_{eq}$ are needed to implement the moving-boundary model for isothermal dehydration, presented and analyzed in Section 3.

3. Mathematical Models

In this section, we briefly review the basic equations of the moving-boundary model for food isothermal dehydration, developed in [13,14].

The transport equation describing the space-time evolution of the pointwise water concentration $c_w(\mathbf{x},t)$ inside the bean, whose volume $V\left(t\right)$ and surface $S\left(t\right)$ are evolving in time, is the following advection-diffusion equation accounting for the local shrinkage through the pointwise shrinkage velocity $\mathbf{v}\left(\mathbf{x}\right)$

$$\frac{\partial c_w(\mathbf{x},t)}{\partial t}+\nabla ·\left(\mathbf{v}\left(\mathbf{x}\right)c_w(\mathbf{x},t)\right)=-\nabla ·\mathbf{J}=\nabla ·\left(D\nabla c_w(\mathbf{x},t)\right),\mathbf{x}\in V\left(t\right)$$

(9)

where $c_w(\mathbf{x},t)$ is the mass concentration of water, $\mathbf{J}=-D\nabla c$ is the diffusive mass flux and $\nabla ·\left(c\mathbf{v}\right)$ is a convective term arising from local shrinkage.

By enforcing the analogy between the dehydration process, in which the sample is releasing water, and the swelling process of rubbery polymers, in which the sample is absorbing water, the pointwise shrinkage velocity $\mathbf{v}$ is assumed proportional (and opposite in sign) to the diffusive (volumetric) flux $\mathbf{J}\left(\mathbf{x}\right)/{\rho }_w$

$$\mathbf{v}=-\alpha \left(c_w\right)\mathbf{J}\left(\mathbf{x}\right)/{\rho }_w=\alpha \left(c_w\right)D\nabla c_w/{\rho }_w,$$

(10)

where $\alpha \left(c_w\right)$ is a shrinkage proportionality factor, depending on the pointwise water concentration.

The shrinkage factor $\alpha \left(c_w\right)$ is the fingerprint of the specific food material under investigation. The simplest case is that of a constant value, i.e., $\alpha \left(c_w\right)={\alpha }_0$. ${\alpha }_0=0$ represents the case of a fully rigid solid (no shrinkage). ${\alpha }_0=1$ represents the case of ideal shrinkage, in which volume reduction corresponds exactly to the volume of water flowing outside the system. Values of ${\alpha }_0$ less or greater than unity imply volume reduction less or greater than the corresponding water volume flow, respectively.

It must be observed that the assumption $\alpha \left(c_w\right)={\alpha }_0$ does not imply that the shrinkage velocity $\mathbf{v}\left(\mathbf{x}\right)$ is constant but rather that, according to Equation (10), the shrinkage velocity is directly proportional to the local concentration gradient. Therefore, the shrinkage velocity asymptotically tends to zero, at each point in the sample, when equilibrium conditions are reached and the water concentration gradient is null everywhere in the system.

The shrinkage velocity $\mathbf{v}\left(\mathbf{x}\right)$ also controls the temporal evolution of the sample boundary $S\left(t\right)$ that evolves in time according to the following equation

$$\frac{d{\mathbf{x}}_b}{dt}=\mathbf{v}{|}_{{\mathbf{x}}_b}=\frac{\alpha \left(c_w\right)}{{\rho }_w}D\nabla c_w{|}_{{\mathbf{x}}_b},{\mathbf{x}}_b\in S\left(t\right).$$

(11)

The two transport equations Equations (9) and (11) are linked together and must be solved simultaneously by further enforcing the following boundary conditions accounting for the flowing water from the boundary $S\left(t\right)$ towards the environment

$$-D\nabla c_w·\mathbf{n}{|}_{{\mathbf{x}}_b}=h_m{\rho }_{air}\left({Y|}_{{\mathbf{x}}_b}-Y_{eq}\right)=h_m{\rho }_{air}\frac{K_{eq}}{{\rho }_s}\left(c_w{|}_{{\mathbf{x}}_b}-c_{w,eq}\right),{\mathbf{x}}_b\in S\left(t\right)$$

(12)

where $\mathbf{n}$ is the outward-pointing normal unit vector, $h_m$ is a mass transfer coefficient (m/s), Y is the air moisture content (kg water/kg dry air), ${\rho }_{air}$ is the air density on dry basis (kg dry air/m${}^3$), ${\rho }_s$ is the solid (pulp) density (kg pulp/m${}^3$product) and $K_{eq}$ is the water partition ratio between the gas and the solid phases $Y=K_{eq}c/{\rho }_s$. The subscript $eq$ stands for equilibrium values.

By introducing the water volume fraction $\varphi \left(\mathbf{x}\right)=c_w\left(\mathbf{x}\right)/{\rho }_w$, the dimensionless space and time variables $\tau =tD/L_r^2$, $\tilde{\mathbf{x}}=\mathbf{x}/L_r$, $\tilde{V}=V/L_r^3$, $\tilde{S}=S/L_r^2$ and the dimensionless differential operators $\tilde{\nabla }=\nabla /L_r$, $\tilde{\nabla }·=\frac{\nabla }{L_r}·$, $L_r$ being a characteristic reference length, the moving-boundary model equations attain the form:

$$\frac{\partial \varphi }{\partial \tau }=\tilde{\nabla }·\left(\tilde{\nabla }\varphi -\left(\alpha \nabla \varphi \right)\varphi )\right)=\tilde{\nabla }·\left(\tilde{\nabla }\varphi (1-\alpha \varphi )\right),\tilde{\mathbf{x}}\in \tilde{V}\left(\tau \right)$$

(13)

$$-\tilde{\nabla }{\varphi ·\mathbf{n}|}_{{\tilde{\mathbf{x}}}_b}=B{i}_m\left({\varphi |}_{{\tilde{\mathbf{x}}}_b}-{\varphi }_{eq}\right),{\tilde{\mathbf{x}}}_b\in \tilde{S}\left(t\right)$$

(14)

$$\frac{d{\tilde{\mathbf{x}}}_b}{d\tau }=\alpha \tilde{\nabla }{\varphi |}_{{\tilde{\mathbf{x}}}_b},{\tilde{\mathbf{x}}}_b\in \tilde{S}\left(\tau \right)$$

(15)

where $\alpha =\alpha \left(\varphi \right)$ is the shrinkage factor and $B{i}_m$ is the mass transfer Biot number

$$B{i}_m=\frac{h_m{L}_r}{D}{K}_{eq}\frac{{\rho }_{air}}{{\rho }_s}.$$

(16)

Initial conditions are $\tilde{V}\left(0\right)={\tilde{V}}_0$, $\tilde{S}\left(0\right)={\tilde{S}}_0$ and $\varphi (\tilde{\mathbf{x}},0)={\varphi }_0\left(\tilde{\mathbf{x}}\right)$.

In the next three paragraphs the moving-boundary model is applied to ellipsoidal beans in order to investigate:

• the influence of the ellipsoidal shape on dehydration kinetics in the simplest case of a uniform initial water distribution, i.e., ${\varphi }_0\left(\tilde{\mathbf{x}}\right)=constant$ and in the absence of shrinkage, i.e., $\alpha \left(\varphi \right)=0$;
• the influence of a nonuniform initial water distribution, i.e., ${\varphi }_0\left(\tilde{\mathbf{x}}\right)={\varphi }_0^{core}$ for $\tilde{\mathbf{x}}\in {\tilde{V}}^{core}$ and ${\varphi }_0\left(\tilde{\mathbf{x}}\right)={\varphi }_0^{shell}$ for $\tilde{\mathbf{x}}\in {\tilde{V}}^{shell}$, on dehydration rates, in the absence of shrinkage, $\alpha \left(\varphi \right)=0$;
• the influence, on dehydration rates, of a constant shrinkage factor $\alpha \left(\varphi \right)={\alpha }_0$.

The ellipsoidal beans analyzed in the next three paragraphs have the three principal axes $a_0=25$ mm, $b_0=13$ mm, $c_0=9$ mm and the shell thickness is ${\lambda }_0=0.5$ mm, an therefore the ratio $V_0^{core}/V_0\simeq 0.787$. The reference length is $L_r=c_0=9$ mm and the initial water volume fraction (averaged over the entire bean, shell and core) is ${\varphi }_0=0.5$.

The 3-d moving-boundary model was numerically solved using finite elements method (FEM) in COMSOL Multiphysics^® v. 3.5. (COMSOL AB, Stockholm, Sweden). The convection-diffusion package (conservative form) was coupled with ALE (Arbitrary Lagrangian Eulerian) moving mesh, allowing re-meshing during the time evolution of the physical domain. Free displacement induced by boundary velocity conditions was set. Lagrangian quadratic elements were chosen. The linear solver adopted is UMFPACK, with relative tolerance ${10}^{-3}$ and absolute tolerance ${10}^{-6}$. The number of finite elements was $4\times {10}^5$–$6\times {10}^5$ with a non-uniform mesh. Smaller elements (minimum element size 0.01 dimensionless unit) have been located close to the moving boundary and to the core/shell boundary in order to accurately compute concentration gradients controlling the velocity of the moving front and the water transport at the core/shell interface. Figure 3 shows the computational domain (1/4 of the ellipsoidal bean) and the FEM mesh adopted.

3.1. Uniform Initial Water Distribution (No Shrinkage)

If we assume no volume shrinkage, i.e., $\alpha \left(\varphi \right)=0$ and $\mathbf{v}\left(\tilde{\mathbf{x}}\right)=0$, the transport equation Equation (13) is a pure diffusion equation on a fixed 3-d domain $\tilde{V}\left(\tau \right)={\tilde{V}}_0$, to be solved with the boundary condition Equation (14) on a fixed surface $\tilde{S}\left(\tau \right)={\tilde{S}}_0$. The uniform initial water distribution inside the bean implies $\varphi (\tilde{\mathbf{x}},0)={\varphi }_0^{core}={\varphi }_0^{shell}={\varphi }_0$ corresponding to unitary partition coefficients ${\beta }_0^{core}={\beta }_0^{shell}=1$, see Equation (4).

Figure 4A shows the behaviour of the moisture ratio $X_r=\frac{(X-X_{eq})}{(X_0-X_{eq})}$ vs. the dimensionless time $\tau =\frac{tD}{L_r^2}$ for different values of the Biot number $B{i}_m=1,2,3,5,9$. Figure 4B shows the same data on a log-normal plot and the perfect agreement with the asymptotic exponential behaviour (dashed lines)

$$X_r=\frac{X-X_{eq}}{X_0-X_{eq}}\sim exp\left[-{\gamma }_0^2{\left(\frac{L_r}{R_{eq}}\right)}^2\tau \right]forlarge\tau$$

(17)

where ${\gamma }_0$ is the smallest positive root of the equation [17,18]

$$\gamma cot(\gamma )+B{i}_m^{eq}-1=0,B{i}_m^{eq}=B{i}_m\left(\frac{R_{eq}}{L_r}\right)$$

(18)

and $B{i}_m^{eq}$ is the equivalent mass Biot number, i.e., the Biot number for a sphere with the same surface-to-volume ratio as the ellipsoidal bean, therefore a sphere with radius $R_{eq}$

$$\frac{4\pi R_{eq}^2}{(4/3)\pi R_{eq}^3}=\frac{S^{ellipsoid}}{V^{ellipsoid}}\to R_{eq}=3\frac{V^{ellipsoid}}{S^{ellipsoid}}=3\frac{(\pi /6)a_0{b}_0{c}_0}{4\pi {\left(\frac{a_0^p{b}_0^p+a_0^p{c}_0^p+b_0^p{c}_0^p}{3}\right)}^{1/p}}$$

(19)

where $p\simeq 1.6075$.

For the cocoa bean under investigation, $R_{eq}\simeq 6.3$ mm, $R_{eq}/L_r=R_{eq}/c_0\simeq 0.7$ and therefore $B{i}_m^{eq}\simeq 0.7B{i}_m$. The corresponding values of ${\gamma }_0$ for different values of $B{i}_m$ are reported in

Table 2. Values of ${\gamma }_0$ for $R_{eq}/L_r=0.7$ and different values of $B{i}_m$.

	${\mathbf{Bi}}_{\mathit{m}}=1$	${\mathbf{Bi}}_{\mathit{m}}=2$	${\mathbf{Bi}}_{\mathit{m}}=3$	${\mathbf{Bi}}_{\mathit{m}}=5$	${\mathbf{Bi}}_{\mathit{m}}=7$	${\mathbf{Bi}}_{\mathit{m}}=9$
${\gamma }_0$	1.35252	1.79058	2.06105	2.38064	2.56061	2.67429

. It can be observed that ${\gamma }_0$ is an increasing function of $B{i}_m$ and only in the limit of $B{i}_m\to \infty$, meaning that the mass transfer resistance at the solid-air interface is negligible, then ${\gamma }_0\to \pi$.

Following reasonings similar to Paramo et al. [11], it is straightforward to verify that the exponential behaviour in Equations (17) and (18), which settles down for long/intermediate dehydration time-scales, implies a linear behaviour for the dimensionless dehydration rate $J_d$ vs. $X_r$ for small/intermediate values of $X_r$

$$J_d=-\frac{d{X}_r}{d\tau }={\gamma }_0^2{\left(\frac{L_r}{R_{eq}}\right)}^2{X}_{r}forsmall{X}_r$$

(20)

as shown in Figure 5.

Equation (20) can be used, in a direct way, to estimate the effective water diffusivity D from the initial linear scaling of the experimental dehydration-rate curves $j_d=-\frac{d{X}_r}{dt}$ vs. t. Indeed, by recalling that $\tau =tD/L_r^2$, Equation (20) can be rewritten as

$$j_d=-\frac{d{X}_r}{dt}=D\frac{{\gamma }_0^2}{R_{eq}^2}{X}_{r}forsmall{X}_r$$

(21)

where ${\gamma }_0$ and $R_{eq}$ are given by Equations (18) and (19), respectively and the only unknown quantity is D. However, the estimate of D from Equation (21) and from the initial slope $\delta$ (h${}^{-1}$) of the experimental dehydration-rate curve $j_d=\delta X_r$ is not so straightforward as it requires the solution of a nonlinear equation for D because ${\gamma }_0$ is a nonlinear function of $B{i}_m$ and $B{i}_m$ depends on D itself, see Equation (16).

Equation (17), or equivalently Equation (20), implies that the dehydration curve of an ellipsoidal bean, on intermediate/long time-scales, can be very accurately approximated by the dehydration curve of a spherical bean with the same surface-to-volume ratio, i.e., with an equivalent radius $R_{eq}$ given by Equation (19).

This finding gives an ultimate answer to the recurring question about how to approximate an ellipsoidal bean for solving the transport equations in a simplified geometry. For example, Herman et al. [9] approximated the ellipsoidal cocoa bean with a cylinder (see Section 2 for details).

Koua et al. [7], following Delgato et al. [19], and Chayjan and Kaveh [20], approximated the ellipsoidal bean with a sphere with the geometric mean radius $R_g=\frac{1}{2}{\left(abc\right)}^{1/3}$. For the ellipsoidal bean under investigation, $R_g\simeq 7.15$ mm that is significantly larger than the equivalent radius $R_{eq}\simeq 6.3$ mm evaluated from Equation (19). The adoption of $R_g$ instead of $R_{eq}$ in Equation (21) would lead to an overestimate of the effective diffusivity D by a factor ${(R_g/R_{eq})}^2\simeq 1.288$ and therefore to a percentage error of about 28%, and this without considering the further error in the overestimation of the equivalent Biot number $B{i}_m^{eq}$, and therefore of ${\gamma }_0$, Equation (18).

Ndukwu et al. [21], following Asoegwu [22] proposed to approximate the ellipsoidal bean with a sphere with an equivalent radius $R_{av}=\frac{1}{3}(R_g+R_a+R_s)$ given by the average between the geometric mean radius $R_g=\frac{1}{2}{\left(abc\right)}^{1/3}$, the arithmetic mean radius $R_a=\frac{1}{6}(a+b+c)$ and the square mean radius $R_s=\frac{1}{2}{[(ab+bc+ac)/3]}^{1/2}$. For the ellipsoidal bean under investigation, $R_{av}\simeq 7.48$ mm, even bigger that $R_g$ and this would lead to an overestimation error for D of about 41%.

3.2. Non-Uniform Initial Water Distribution (No Shrinkage)

In this paragraph, the influence of a non-uniform initial water distribution on dehydration-rate curves is investigated, in the absence of bean shrinkage, i.e., $\alpha \left(\varphi \right)=0$.

Also in this case, as in Section 3.1, the transport equation Equation (13) is pure diffusion equation on a fixed 3-d domain $\tilde{V}\left(\tau \right)={\tilde{V}}_0$, to be solved with the boundary condition Equation (14) on a fixed surface $\tilde{S}\left(\tau \right)={\tilde{S}}_0$. What changes is the initial condition for the water distribution, because in this case $\varphi \left(\tilde{\mathbf{x}},0\right)={\varphi }_0^{core}$ for $\tilde{\mathbf{x}}\in {\tilde{V}}^{core}$ and $\varphi \left(\tilde{\mathbf{x}},t\right)={\varphi }_0^{shell}$ for $\tilde{\mathbf{x}}\in {\tilde{V}}^{shell}$, with ${\varphi }_0^{core}\ne {\varphi }_0^{shell}$.

Specifically, we analyze two different initial conditions, namely ${\beta }_0^{core}=0.9$ (that implies ${\beta }_0^{shell}\simeq 1.35$) and ${\beta }_0^{core}=0.8$ (that implies ${\beta }_0^{shell}\simeq 1.74$), both corresponding to the case in which ${\varphi }_0^{shell}>{\varphi }_0^{core}$.

Figure 6 shows the dimensionless dehydration rate $J_d$ vs. the moisture ratio $X_r$ for different values of $B{i}_m$, for a uniform initial water distribution, ${\beta }_0^{core}={\beta }_0^{shell}=1$ (continuous lines) and for the two non-uniform initial water distributions (dashed lines), ${\beta }_0^{core}=0.9,0.8$. The higher the value of water concentration in the shell ${\varphi }_0^{shell}$, the faster the decrease of the total moisture content at the beginning of the drying process, and therefore the larger the initial dehydration rate $J_d$. The larger the $B{i}_m$, the larger the influence of initial water non-uniformity on dehydration-rate curves.

It should be further observed that in the absence of shrinkage, the linear scaling of $J_d$ vs. $X_r$ for small $X_r$ (long dehydration time-scales) is almost unaffected by the initial non-uniform water distribution so that Equation (21) can be still applied to estimate the effective water diffusion coefficient D.

3.3. The Influence of Shrinkage on Dehydration Curves

Sample shrinkage strongly influences the dehydration curves because the progressive decrease in volume leads to a reduction of the diffusional paths. If the water diffusivity D is assumed to be independent of the local water concentration, shrinkage accelerates the dehydration process and dehydration rates are higher.

Figure 7 shows the behaviour of the dehydration-rate curves for different values of $B{i}_m$ and increasing values of a constant shrinkage factor $\alpha \left(\varphi \right)={\alpha }_0=0,0.1,0.3,0.5$. The dehydration-rate curves shown in Figure 7 was obtained by numerically integrating the moving-boundary transport model Equations (13)–(15) for a uniform initial water distribution $\varphi (\tilde{\mathbf{x}},0)={\varphi }_0^{core}={\varphi }_0^{shell}={\varphi }_0$.

The assumption of a constant shrinkage factor $\alpha \left(\varphi \right)={\alpha }_0$ does not imply a constant shrinkage velocity but rather that the pointwise shrinkage velocity is proportional to the local water concentration gradient with a proportionality constant that is uniform inside the sample and constant during the course of the dehydration process.

A constant shrinkage factor $\alpha \left(\varphi \right)={\alpha }_0$ implies a linear “calibration curve”, i.e., a linear relationship between volume reduction $[1-\frac{V\left(t\right)}{V_0}]$ and moisture content reduction $[1-\frac{X\left(t\right)}{X_0}]$

$$\left[1-\frac{V}{V_0}\right]={\alpha }_0{\varphi }_0\left[1-\frac{X}{X_0}\right]⟶\frac{V_{eq}}{V_0}=1-{\alpha }_0{\varphi }_0\left(1-\frac{X_{eq}}{X_0}\right).$$

(22)

When the moisture content reaches its asymptotic/equilibrium value $X_{eq}$ and $X_{eq}\ll X_0$, the final sample volume $V_{eq}/V_0$ can be approximated as $V_{eq}/V_0\simeq 1-{\alpha }_0{\varphi }_0$.

The different dehydration-rate curves, shown in Figure 7, obtained for increasing values of ${\alpha }_0$, from ${\alpha }_0=0$ (no shrinkage) to ${\alpha }_0=0.5$, correspond to decreasing values of the final sample volume, namely $V_{eq}/V_0=1,0.95,0.85,0.75$, the latter two values very close to that observed from experimental cocoa bean shrinkage data (see Section 2). As expected, the higher ${\alpha }_0$, the higher the dehydration rates, and this effect is amplified for higher $B{i}_m$ values.

It can be further observed that shrinkage also affects the linear scaling of $J_d$ vs. $X_r$ for small $X_r$ (long dehydration time-scales). In the presence of shrinkage, this linear scaling can still be estimated from Equations (18) and (20), valid in the absence of shrinkage, by simply replacing the equivalent radius $R_{eq}$ with the equivalent radius ${\tilde{R}}_{eq}=R_{eq}{\left(\frac{V_{eq}}{V_0}\right)}^{1/3}$, in which enters the factor ${\left(\frac{V_{eq}}{V_0}\right)}^{1/3}$, accounting for volume reduction on longer time-scales, thus obtaining

$$J_d={\tilde{\gamma }}_0^2{\left(\frac{L_r}{{\tilde{R}}_{eq}}\right)}^2{X}_r={\tilde{\gamma }}_0^2{\left(\frac{L_r}{R_{eq}}\right)}^2{\left(\frac{V_{eq}}{V_0}\right)}^{-2/3}{X}_r\mathrm{for}\mathrm{small}{X}_r$$

(23)

where ${\tilde{\gamma }}_0^2$ is the smallest positive root of the equation

$$\tilde{\gamma }cot(\tilde{\gamma })+\tilde{B}{i}_m^{eq}-1=0,\tilde{B}{i}_m^{eq}=B{i}_m\left(\frac{{\tilde{R}}_{eq}}{L_r}\right)=B{i}_m\left(\frac{R_{eq}}{L_r}\right){\left(\frac{V_{eq}}{V_0}\right)}^{1/3}$$

(24)

Figure 8 shows the excellent agreement between the dehydration-rate curves for ${\alpha }_0=0.5$ and the theoretical linear behaviour, Equations (23) and (24) with $R_{eq}/L_r=0.7$, $V_{eq}/V_0\simeq 0.85$ and with the values of ${\tilde{\gamma }}_0$, derived from Equation (24), reported in

Table 3. Values of ${\tilde{\gamma }}_0$ for $R_{eq}/L_r=0.7$, ${\alpha }_0=0.5$, $V_{eq}/V_0=0.85$ and different values of $B{i}_m$.

	${\mathbf{Bi}}_{\mathit{m}}=1$	${\mathbf{Bi}}_{\mathit{m}}=2$	${\mathbf{Bi}}_{\mathit{m}}=3$	${\mathbf{Bi}}_{\mathit{m}}=5$	${\mathbf{Bi}}_{\mathit{m}}=7$	${\mathbf{Bi}}_{\mathit{m}}=9$
${\tilde{\gamma }}_0$	1.29016	1.71879	1.98915	2.31671	2.50135	2.62754

.

Therefore, also in the presence of shrinkage, the effective water diffusivity D can be estimated from the slope $\delta$ (h${}^{-1}$) of the initial linear scaling of the experimental dehydration-rate curve $j_d=\delta X_r$ by solving the nonlinear equation for D

$$\delta =D{\left(\frac{{\tilde{\gamma }}_0}{R_{eq}}\right)}^2{\left(\frac{V_{eq}}{V_0}\right)}^{-2/3}$$

(25)

where ${\tilde{\gamma }}_0$ depends on $B{i}_m$ and $B{i}_m$ depends on D, Equation (16).

In the next section we make a direct use of Equation (25) to estimate the effective water diffusivity D in cocoa beans by analyzing the experimental dehydration curves reported by Herman et al. [9,10].

4. Analysis of Dehydration Kinetics and Shrinkage of Ellipsoidal Cocoa Beans

We analyze the experimental dehydration curves of ellipsoidal fermented Amazonian cocoa beans reported by Herman et al. [9,10] and verify the capability of the moving-boundary model, accounting for nonuniform initial water distribution inside the core and the shell and sample shrinkage, to describe and capture all the complex features of the dehydration kinetics of cocoa beans.

The shrinkage factor $\alpha \left(\varphi \right)$ was assumed constant $\alpha \left(\varphi \right)={\alpha }_0$ and estimated from Equation (22) for both data sets. A review of all the physical, geometrical and shrinkage parameters adopted in the moving-boundary model for the analysis of data set (1) and (2) are reported in

Table 4. Review of physical, geometrical and shrinkage parameters adopted in the moving-boundary model for the analysis of data set (1) and (2).

Data Set	${\mathit{\varphi }}_0$	${\mathit{R}}_{\mathbf{eq}}$ (mm)	${\mathit{\beta }}_0^{\mathbf{core}}$	${\mathit{\beta }}_0^{\mathbf{shell}}$	${\mathit{V}}_{\mathbf{eq}}/{\mathit{V}}_0$	${\mathit{\varphi }}_{\mathbf{eq}}$	${\mathit{\alpha }}_0$
	Equation (2)	Equation (19)	Equation (4)	Equation (4)	Equations (5) & (6)	Equation (8)	Equation (22)
(1)	0.57	6.23	0.912	1.35	0.82	0.038	0.33
(2)	0.59	6.13	0.78	1.53	0.78	0.042	0.39

.

In Section 4.1, the effective water diffusivity D, at different drying temperatures, is estimated, starting from the experimental dehydration curves for cocoa beans characterized by a lower non-uniformity of the initial water distribution between core and shell, data set (1).

In Section 4.2 the moving-boundary model is adopted, in a fully predictive way, to evaluate the dehydration curves for different air velocities for cocoa beans of data set (1). Moreover, the moving-boundary model is applied to predict the dehydration curves for cocoa beans characterized by a higher non-uniformity of the initial water distribution and a larger shrinkage (data set (2)).

In Section 4.3 a detailed comparison between model predictions and experimental data for the temporal evolution of the moisture content and thickness of core and shell is presented. The influence of shrinkage is addressed in detail.

4.1. Estimate of Water Effective Diffusivity D

Figure 9A,B show the influence of the drying temperature on the dehydration kinetics of cocoa beans of data set (1) for a fixed air velocity $v=0.6$ m/s. Figure 9A shows the temporal decay of the rescaled moisture content $X\left(t\right)/X_0$ of the entire bean (core and shell) while Figure 9B shows the behaviour of the dimensional dehydration rate $j_d$ (h${}^{-1}$) vs. $X_r$. For each temperature T, the dehydration-rate curve $j_d$ vs. $X_r$ has been obtained from a best fit of the dehydration curve $X/X_0$ vs. t, at the same temperature T, with the following function

$$X\left(t\right)/X_0=a_0+a_1{e}^{-b_{1}t}+a_2{e}^{-b_{2}t}+(1-a_0-a_1-a_2)e^{-b_{3}t},$$

superposition of three exponential functions of time plus a constant and satisfying the two constrains $X\left(0\right)/X_0=1$, $X_{eq}/X_0=a_0$;

The dehydration rate $j_d\left(t\right)$ has been subsequently evaluated as

$$j_d=-\frac{d{X}_r}{dt}=-\frac{d}{dt}\left[\frac{X-X_{eq}}{X_0-X_{eq}}\right]=\frac{d(X/X_0)}{dt}\frac{-1}{1-X_{eq}/X_0},$$

hence

$$j_d=\frac{1}{1-a_0}\left(a_1{b}_1{e}^{-b_{1}t}+a_2{b}_2{e}^{-b_{2}t}+(1-a_0-a_1-a_2)b_3{e}^{-b_{3}t}\right),$$

plotted as a function of $X_r=\frac{(X\left(t\right)/X_0)-a_0}{1-a_0}$.

As expected, the synergistic effect of a larger moisture content in the shell and of shrinkage leads to high values of the dehydration rate at the beginning of the drying process (large $X_r$) and a rapid decrease of $j_d$ towards the asymptotic linear scaling $j_d=\delta \left(T\right)X_r$, valid for smaller values of $X_r$.

From the experimental values of $\delta \left(T\right)$ and Equation (25), it is possible to evaluate the minimum value of the water diffusivity $D_{min}\left(T\right)$ at different temperatures, i.e., the value of the water diffusivity that would be estimated if the mass transfer resistance at the solid/air interface were neglected. Indeed, $D_{min}\left(T\right)$ can be readily estimated from $\delta \left(T\right)$ and Equation (25) by assuming $h_m\to \infty$, which implies $B{i}_m\to \infty$ and therefore ${\gamma }_0\to \pi$. The value of the actual water diffusivity $D\left(T\right)$ is necessarily greater than $D_{min}\left(T\right)$ because, for any finite value of $B{i}_m$, ${\gamma }_0<\pi$.

The values of $D_{min}$, together with the optimized values of D (and the corresponding $B{i}_m$), obtained by a best fit of numerical data from the moving-boundary model onto the experimental data, for different drying temperatures, are reported in

Table 5. Estimated water diffusivities $D_{min}$, D and Biot number $B{i}_m$ for cocoa beans of data set (1) for different drying temperatures T and $v=0.6$ m/s.

	$\mathit{T}=30{}^{\circ }$C	$\mathit{T}=40{}^{\circ }$C	$\mathit{T}=50{}^{\circ }$C	$\mathit{T}=60{}^{\circ }$C
$D_{min}$ (m${}^2$/s)	$(7.65\pm 0.1)\times {10}^{-11}$	$(1.34\pm 0.03)\times {10}^{-10}$	$(1.62\pm 0.05)\times {10}^{-10}$	$(2.48\pm 0.03)\times {10}^{-10}$
D (m${}^2$/s)	$(9.11\pm 0.1)\times {10}^{-11}$	$(1.54\pm 0.03)\times {10}^{-10}$	$(2.09\pm 0.05)\times {10}^{-10}$	$(3.12\pm 0.03)\times {10}^{-10}$
$B{i}_m$	$(17.93\pm 0.1)$	$(16.24\pm 0.1)$	$(14.83\pm 0.1)$	$(13.61\pm 0.12)$

. The excellent agreement between the experimental data (points) and the numerical results of the moving-boundary model (continuous lines) is shown in Figure 9A and B both for the dehydration curves and the dehydration-rate curves.

The diffusivity values $D\left(T\right)$ are plotted in Figure 10, as a function of T, together with the Arrhenius function $D=D_{0}exp[-E/(RT\left)\right]$ with $D_0=5.77\times {10}^{-5}$ m${}^2$/s and $E/R=4037.78$ (K). These values are slightly larger than that reported by Herman et al. [9] ($D\left(T\right)\in [(6.8\pm 0.17)\times {10}^{-11}÷(1.41\pm 0.19)\times {10}^{-10}]$ m${}^2$/s for $T\in$ [30 ${}^{\circ }$C ÷ 60 ${}^{\circ }$C]) that are, however, all below the minimum values $D_{min}\left(T\right)$ reported in Table 5.

4.2. Influence of Air Velocity and Non-Uniformity of the Initial Water Distribution

The moving-boundary model is adopted, in a fully predictive way, to investigate the influence of air velocity of the dehydration kinetics.

Figure 11A and B show experimental data (points) for the dehydration curves $X/X_0$ vs. t (h) and for the dehydration-rate curves $j_d$ vs. $X_r$ at $T=60$${}^{\circ }$C for three different air velocities, $v=0.3,0.6,1$ m/s, as reported by Herman et al. for cocoa beans of data set (1).

Continuous lines are model predictions with D(60 ${}^{\circ }$C) = $3.12\times {10}^{-10}$ m${}^2$/s (see Table 5) and with different values of $B{i}_m$, namely $B{i}_m=10.27,13.61,16.93$ for $v=0.3,0.6,1$ m/s, respectively. The mass transfer coefficient $h_m$, entering the $B{i}_m$ number, was estimated, for different velocities v, from the classical Fr$\ddot{o}$ssling correlation [23] for the Sherwood number, valid for spheres

$$Sh=2+0.6R{e}^{1/2}S{c}^{1/3}$$

(26)

where the equivalent radius $R_{eq}=6.23$ mm for cocoa beans of data set (1) was used both in the Sherwood number and in the Reynolds number.

The moving-boundary model accurately describes the sensitivity of the dehydration curves to the air velocity and quantitatively predicts the slight increase of the dehydration rates for increasing Reynolds numbers.

The moving-boundary model can also accurately predict the influence of the non-uniformity of the initial water distribution on the dehydration kinetics. Indeed, Figure 12 shows the excellent agreement between experimental dehydration kinetics and model predictions for both data set (1) (data already shown in Figure 9A,B) and data set (2) for $T=60$${}^{\circ }$C and $v=0.6$ m/s. Cocoa beans of data set (2) are characterized by a larger shell moisture content ${\beta }_0^{shell}=1.53$ and a slightly larger asymptotic shrinkage $V_{eq}/V_0=0.78$, if compared to that of data set (1), see Table 4. Both these features contribute to a faster initial decay of the rescaled moisture content $X\left(t\right)/X_0$ and therefore to larger initial dehydration rates, perfectly predicted by the moving-boundary model with the same value of the water diffusivity D(60 ${}^{\circ }$C) = $3.12\times {10}^{-10}$ m${}^2$/s and the mass Biot number $B{i}_m=12.87$ directly obtained from the value $B{i}_m=13.61$, previously evaluated for cocoa beans of data set (1), by replacing the reference length $L_r$ and the equivalent radius $R_{eq}$ of data set (1) with the corresponding values for data set (2), see Table 4. It should be further observed that the dehydration-rate curves, for both data sets (1) and (2), almost overlap one another on longer dehydration time-scales. This asymptotic behaviour, well captured by the moving-boundary model, is in agreement with what is expected by considering that the water diffusivity D may be assumed the same for both types of cocoa beans and also the equivalent radii $R_{eq}$ for data set (1) and (2) are very close each other.

4.3. Temporal Evolution of the Moisture Content and Thickness of Core and Shell

The moving-boundary model can accurately predict not only the temporal evolution of the total moisture content $X\left(t\right)=X^{core}\left(t\right)+X^{shell}\left(t\right)$ of the cocoa bean, but also the evolution, during the dehydration process, of the two specific moisture contents, namely that of the core $X^{core}$ and of the shell $X^{shell}$, plotted as a function of the total moisture content X in Figure 13 for cocoa beans of data set (2), as reported by Herman et al. [10].

Continuous lines in Figure 13 show the model predictions for the moving-boundary model accounting for shrinkage, while dashed lines indicate model predictions without shrinkage. Both approaches give quite satisfactorily results but that accounting for shrinkage better describes the almost constant behaviour $X^{core}\simeq X_0^{core}$ at short/intermediate time scales, corresponding to $0.5\le X\le X_0$. Both experimental data and theoretical results support the physical observation that the initial moisture content decay is mainly due to the dehydration of the bean shell.

In point of fact, although the volume contraction is not very large (about 30%), shrinkage effect must be necessarily taken into account for an accurate description of the dehydration curves and for a reliable estimate of the water diffusivity D.

The comparison between experimental data and model predictions for the evolution of the lengths of the three principal axes of the cocoa bean and of the shell thickness of data set (2), during the dehydration process, is shown in Figure 14. It can be observed that, despite the extremely noisy experimental data of axes lengths and shell thickness, the model predictions can be considered quite satisfactory since they are able to capture general trends of all the quantities.

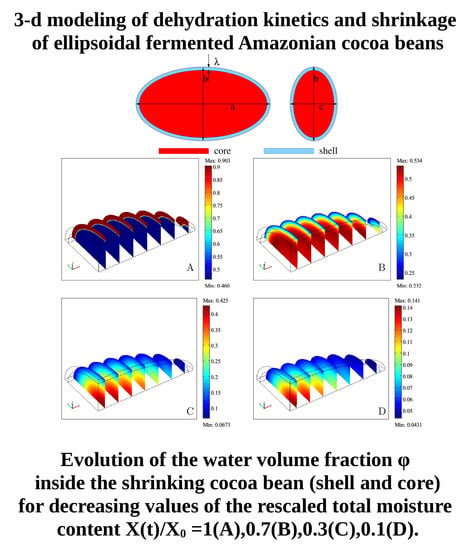
Figure 15A–D show the evolution, during the drying process, of the water volume fraction $\varphi (\tilde{\mathbf{x}},t)$ inside the shrinking bean (shell and core), for decreasing values of the rescaled total moisture content $X\left(t\right)/X_0=1,0.7,0.3,0.1$. The initial position of the external boundary (solid/air interface) and of the internal boundary (shell/core interface) are highlighted in order to have a better visualization of the progressive shrinkage of the bean.

5. Conclusions

The moving-boundary model for food isothermal dehydration, developed in [13,14], was applied to analyze the dehydration kinetics of ellipsoidal cocoa beans, characterized by a non-uniform initial distribution of the moisture content between the core and the shell.

The model proved capable of accurately describing the two-phases dehydration process: an initial fast dehydration of the shell, characterized by higher dehydration rates, followed by a slower dehydration of the core, characterized by a linear relationship $j_d=\delta \left(T\right)X_r$ between the dehydration rate $j_d$ and the moisture ratio $X_r$.

Specifically, from this linear behaviour, a shortcut method to estimate the effective water diffusivity D is proposed, based on Equation (25), and derived from the basic observation that the asymptotic exponential behaviour of the dehydration curve $X_r\left(t\right)$ vs. t for an ellipsoidal bean coincides with that of an equivalent sphere, with radius $R_{eq}$ given by Equation (19), with the same surface-to-volume ratio as the original ellipsoid.

The moving-boundary model was successfully applied to predict the influence of air velocity and non-uniformity of the initial water distribution on the dehydration rates, as well as to predict the temporal evolution of the water content in the core and in the shell and of the characteristic lengths of the ellipsoidal bean.