Dynamic Optimization of a Fed-Batch Nosiheptide Reactor
Abstract
:1. Introduction
1.1. Nosiheptide
1.2. Process Modeling and Optimization Studies
1.3. This Work
2. Dynamic Process Modeling, Simulation, and Optimization Methodology
2.1. Nosiheptide Fed-Batch Fermentation Model and Parameter Estimation
2.1.1. Dynamic Process Model
2.1.2. Model Parameter Estimation
2.2. Dynamic Simulation
2.3. Dynamic Optimization
2.3.1. Problem Statement
2.3.2. Solution Method
2.3.3. Optimization Objectives and Strategy
3. Results and Discussion
3.1. Dynamic Simulation and Design Space Visualization
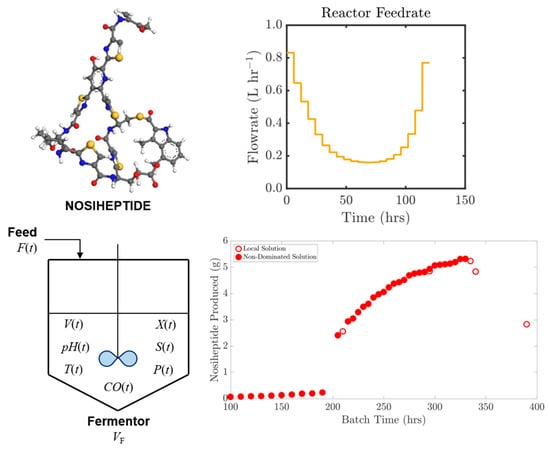
3.2. Optimal Reactor Reactor Feedrate Policy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| AE | Algebraic equation |
| ANN | Artificial neural network |
| API | Active pharmaceutical ingredient |
| CHO | Chinese hamster ovary |
| DAE | Differential algebraic equation |
| IPOPT | Interior point optimizer |
| mAb | Monoclonal antibody |
| MRSA | Methicillin-resistant Staphylococcus aureus |
| NLP | Nonlinear programming |
| ODE | Ordinary differential equation |
| PGA | Penicillin G acylase |
| UTI | Urinary tract infection |
| VRE | Vancomycin-resistant Enterococci |
| Variables | |
| Latin Letters | |
| Ad | Death pre-exponent (–) |
| Ag | Growth pre-exponent (–) |
| CO | Dissolved oxygen concentration (g L−1) |
| CO* | Saturation dissolved oxygen concentration (g L−1) |
| D | Fermentation vessel diameter (m) |
| d | Agitator diameter (m) |
| Ed | Energy barrier to death (J mol−1) |
| Eg | Energy barrier to growth (J mol−1) |
| F | Reactor feeding rate (L h−1) |
| g | Inequality constraint vector |
| gf | Terminal inequality constraint vector |
| h | Equality constraint vector |
| hf | Terminal equality constraint vector |
| K | Number of collocation points |
| K1, K2 | Constants in Equation (2) |
| Kd | Monod constant (g L−1) |
| Kh | Equilibrium constant (h−1) |
| KO | Contois saturation constant of dissolved oxygen (–) |
| KS | Contois saturation constant of substrate (–) |
| KLa | Volumetric oxygen transfer coefficient (h−1) |
| mO | Maintenance coefficient of dissolved oxygen (g g−1 h−1) |
| mS | Maintenance coefficient of substrate (g g−1 h−1) |
| MSE | Mean squared error |
| N | Number of control elements |
| n | Stirring rate (rpm) |
| P | Product concentration (g L−1) |
| Pi | Stirring power (W) |
| Q | Fermentor ventilation volume (m3 h−1) |
| R | Universal gas constant (= 8.314 J mol−1K−1) |
| S | Substrate concentration (g L−1) |
| SSE | Sum of squared errors |
| T | Temperature (K) |
| t | Time (h) |
| ∆t | Time step (h) |
| tf | Final time (h) |
| t0 | Initial time (h) |
| u | Control variable vector |
| uL | Control variable lower bound vector |
| uU | Control variable upper bound vector |
| V | Fermentation broth volume (L) |
| VF | Fermentor volume (L) |
| X | Biomass concentration (g L−1) |
| x | State variable vector |
| XMAX | Maximum biomass concentration (g L−1) |
| xL | State variable lower bound vector |
| x0 | State initial condition vector |
| xU | State variable upper bound vector |
| YP/O | Yield constant of product vs. dissolved oxygen (g g−1) |
| YP/S | Yield constant of product vs. substrate (g g−1) |
| YX/O | Yield constant of biomass vs. dissolved oxygen (g g−1) |
| YX/S | Yield constant of biomass vs. substrate (g g−1) |
| Greek Letters | |
| β | Specific production rate (g g−1 h−1) |
| ε | Batch duration constraint (h) |
| θ | Parameter vector |
| φ | Objective function |
| Ωj | jth-order polynomial |
| ψj | jth-order Lagrange polynomial |
| μd | Specific death rate (h−1) |
| μg | Specific growth rate (h−1) |
References
- Zaffiri, L.; Gardner, J.; Toledo-Pereyra, L.H. History of antibiotics. from salvarsan to cephalosporins. J. Investig. Surg. 2012, 25, 67–77. [Google Scholar] [CrossRef]
- Russell, M.G.; Jamison, T.F. Seven-step continuous flow synthesis of linezolid without intermediate purification. Angew. Chem. Int. Ed. 2019, 58, 7678–7681. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Dai, C.; Jamison, T.F.; Jensen, K.F. A rapid total synthesis of ciprofloxacin hydrochloride in continuous flow. Angew. Chem. Int. Ed. 2017, 56, 8870–8873. [Google Scholar] [CrossRef] [PubMed]
- Volpato, G.; Rodrigues, R.C.; Fernandez-Lafuente, R. Use of enzymes in the production of semi-synthetic penicillins and cephalosporins: Drawbacks and perspectives. Curr. Med. Chem. 2010, 17, 3855–3873. [Google Scholar] [CrossRef] [PubMed]
- Benazet, F.; Cartier, M.; Florent, J.; Godard, C.; Jung, G.; Lunel, J.; Mancy, D.; Pascal, C.; Renaut, J.; Tarridec, P.; et al. Nosiheptide, a sulfur-containing peptide antibiotic isolated from Streptomyces actuosus 40037. Experientia 1980, 36, 414–416. [Google Scholar] [CrossRef]
- Wojtas, K.P.; Riedrich, M.; Lu, J.Y.; Winter, P.; Winkler, T.; Walter, S.; Arndt, H.D. Total synthesis of nosiheptide. Angew. Chem. Int. Ed. 2016, 55, 9772–9776. [Google Scholar] [CrossRef]
- Jolliffe, H.G.; Gerogiorgis, D.I. Technoeconomic optimization of a conceptual flowsheet for continuous separation of an analgaesic active pharmaceutical ingredient (API). Ind. Eng. Chem. Res. 2017, 56, 4357–4376. [Google Scholar] [CrossRef] [Green Version]
- Gerogiorgis, D.I.; Jolliffe, H.G. Continuous pharmaceutical process engineering and economics. Investigating technical efficiency, environmental impact + economic viability. Chem. Today 2015, 33, 29–32. [Google Scholar]
- Yu, Y.; Duan, L.; Zhang, Q.; Liao, R.; Ding, Y.; Pan, H.; Wendt-Pienkowski, E.; Tang, G.; Shen, B.; Liu, W. Nosiheptide biosynthesis featuring a unique indole side ring formation on the characteristic thiopeptide framework. ACS Chem. Biol. 2009, 4, 855–864. [Google Scholar] [CrossRef] [Green Version]
- Shirahata, H.; Diab, S.; Sugiyama, H.; Gerogiorgis, D.I. Dynamic modelling, simulation and economic evaluation of two CHO cell-based production modes towards developing biopharmaceutical manufacturing processes. Chem. Eng. Res. Des. 2019, 150, 218–233. [Google Scholar] [CrossRef]
- Veterinary Antimicrobial Resistance and Sales Surveillance 2018. Available online: https://www.gov.uk/government/publications/veterinary-antimicrobial-resistance-and-sales-surveillance-2018 (accessed on 6 March 2020).
- Gonçalves, L.R.B.; Sousa, R.; Fernandez-Lafuente, R.; Guisan, J.M.; Giordano, R.L.C.; Giordano, R.C. Enzymatic synthesis of amoxicillin: Avoiding limitations of the mechanistic approach for reaction kinetics. Biotechnol. Bioeng. 2002, 80, 622–631. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, L.R.B.; Giordano, R.L.C.; Giordano, R.C. Mathematical modeling of batch and semibatch reactors for the enzymic synthesis of amoxicillin. Process. Biochem. 2005, 40, 247–256. [Google Scholar] [CrossRef]
- Chow, Y.; Li, R.; Wu, J.; Puah, S.M.; New, S.W.; Chia, W.Q.; Lie, F.; Rahman, T.M.R.; Choi, W.J. Modeling and optimization of methanol as a cosolvent in amoxicillin synthesis and its advantage over ethylene glycol. Biotechnol. Bioprocess. Eng. 2007, 12, 390–398. [Google Scholar] [CrossRef]
- Silva, J.A.; Costa Neto, E.H.; Adriano, W.S.; Ferreira, A.L.O.; Gonçalves, L.R.B. Use of neural networks in the mathematical modelling of the enzymic synthesis of amoxicillin catalysed by penicillin G acylase immobilized in chitosan. World J. Microbiol. Biotechnol. 2008, 24, 1761–1767. [Google Scholar] [CrossRef]
- McDonald, M.A.; Bommarius, A.S.; Rousseau, R.W.; Grover, M.A. Continuous reactive crystallization of β-lactam antibiotics catalyzed by penicillin G acylase. Part I: Model development. Comput. Chem. Eng. 2019, 123, 331–343. [Google Scholar] [CrossRef]
- McDonald, M.A.; Bommarius, A.S.; Grover, M.A.; Rousseau, R.W. Continuous reactive crystallization of β-lactam antibiotics catalyzed by penicillin G acylase. Part II: Case study on ampicillin and product purity. Comput. Chem. Eng. 2019, 126, 332–341. [Google Scholar] [CrossRef]
- Cuthbertson, A.B.; Rodman, A.D.; Diab, S.; Gerogiorgis, D.I. Dynamic modelling and optimisation of the batch enzymatic synthesis of amoxicillin. Processes 2019, 7, 318. [Google Scholar] [CrossRef] [Green Version]
- Encarnación-Gómez, L.G.; Bommarius, A.S.; Rousseau, R.W. Crystallization kinetics of ampicillin using online monitoring tools and robust parameter estimation. Ind. Eng. Chem. Res. 2016, 55, 2153–2162. [Google Scholar] [CrossRef]
- McDonald, M.A.; Bommarius, A.S.; Rousseau, R.W. Enzymatic reactive crystallization for improving ampicillin synthesis. Chem. Eng. Sci. 2017, 165, 81–88. [Google Scholar] [CrossRef]
- Dafnomilis, A.; Diab, S.; Rodman, A.D.; Boudouvis, A.G.; Gerogiorgis, D.I. Multi-objective dynamic optimization of ampicillin batch crystallization: Sensitivity analysis of attainable performance vs. product quality constraints. Ind. Eng. Chem. Res. 2019, 58, 18756–18771. [Google Scholar] [CrossRef]
- Schroën, C.G.P.H.; Nierstrasz, V.A.; Moody, H.M.; Hoogschagen, M.J.; Kroon, P.J.; Bosma, R.; Beeftink, H.H.; Janssen, A.E.M.; Tramper, J. Modeling of the enzymatic kinetic synthesis of cephalexin-influence of substrate concentration and temperature. Biotechnol. Bioeng. 2001, 73, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Schroën, C.G.P.H.; Fretz, C.B.; DeBruin, V.H.; Berendsen, W.; Moody, H.M.; Roos, E.C.; VanRoon, J.L.; Kroon, P.J.; Strubel, M.; Janssen, A.E.M.; et al. Modelling of the enzymatic kinetically controlled synthesis of cephalexin: Influence of diffusion limitation. Biotechnol. Bioeng. 2002, 80, 331–340. [Google Scholar] [CrossRef] [PubMed]
- Travascio, P.; Zito, E.; De Maio, A.; Schroën, C.G.P.H.; Durante, D.; De Luca, P.; Bencivenga, U.; Mita, D.G. Advantages of using non-isothermal bioreactors for the enzymatic synthesis of antibiotics: The penicillin G acylase as enzyme model. Biotechnol. Bioeng. 2002, 79, 334–346. [Google Scholar] [CrossRef] [PubMed]
- McDonald, M.A.; Marshall, G.D.; Bommarius, A.S.; Grover, M.A.; Rousseau, R.W. Crystallization kinetics of cephalexin monohydrate in the presence of cephalexin precursors. Cryst. Growth Des. 2019, 19, 5065–5074. [Google Scholar] [CrossRef]
- Farkya, S.; Bisaria, V.S.; Srivastava, A.K. Biotechnological aspects of the production of the anticancer drug podophyllotoxin. Appl. Microbiol. Biotechnol. 2004, 65, 504–519. [Google Scholar] [CrossRef] [PubMed]
- Laursen, S.Ö.; Webb, D.; Ramirez, W.F. Dynamic hybrid neural network model of an industrial fed-batch fermentation process to produce foreign protein. Comput. Chem. Eng. 2007, 31, 163–170. [Google Scholar] [CrossRef]
- Truppo, M.D.; Pollard, D.J.; Moore, J.C.; Devine, P.N. Production of (S)-γ-fluoroleucine ethyl ester by enzyme mediated dynamic kinetic resolution: Comparison of batch and fed batch stirred tank processes to a packed bed column reactor. Chem. Eng. Sci. 2008, 63, 122–130. [Google Scholar] [CrossRef]
- Xing, Z.; Bishop, N.; Leister, K.; Li, Z.J. Modeling kinetics of a large-scale fed-batch CHO cell culture by Markov chain Monte Carlo method. Biotechnol. Prog. 2010, 26, 208–219. [Google Scholar] [CrossRef]
- Song, H.; Eom, M.H.; Lee, S.; Lee, J.; Cho, J.H.; Seung, D. Modeling of batch experimental kinetics and application to fed-batch fermentation of Clostridium tyrobutyricum for enhanced butyric acid production. Biochem. Eng. J. 2010, 53, 71–76. [Google Scholar] [CrossRef]
- Georgakis, C. Design of dynamic experiments: A data-driven methodology for the optimization of time-varying processes. Ind. Eng. Chem. Res. 2013, 52, 12369–12382. [Google Scholar] [CrossRef]
- Kiparissides, A.; Pistikopoulos, E.N.; Mantalaris, A. On the model-based optimization of secreting mammalian cell (GS-NS0) cultures. Biotechnol. Bioeng. 2015, 112, 536–548. [Google Scholar] [CrossRef] [PubMed]
- Robitaille, J.; Chen, J.; Jolicoeur, M. A single dynamic metabolic model can describe mAb producing CHO cell batch and fed-batch cultures on different culture media. PLoS ONE 2015, 10, e0136815. [Google Scholar] [CrossRef] [PubMed]
- Ben Yahia, B.; Gourevitch, B.; Malphettes, L.; Heinzle, E. Segmented linear modeling of CHO fed-batch culture and its application to large scale production. Biotechnol. Bioeng. 2017, 114, 785–797. [Google Scholar] [CrossRef] [PubMed]
- Raftery, J.P.; DeSessa, M.R.; Karim, M.N. Economic improvement of continuous pharmaceutical production via the optimal control of a multifeed bioreactor. Biotechnol. Prog. 2017, 33, 902–912. [Google Scholar] [CrossRef] [PubMed]
- Kappatou, C.D.; Mhamdi, A.; Campano, A.Q.; Mantalaris, A.; Mitsos, A. Model-based dynamic optimization of monoclonal antibodies production in semibatch operation—Use of reformulation techniques. Ind. Eng. Chem. Res. 2018, 57, 9915–9924. [Google Scholar] [CrossRef]
- Hogiri, T.; Tamashima, H.; Nishizawa, A.; Okamoto, M. Optimization of a pH-shift control strategy for producing monoclonal antibodies in Chinese hamster ovary cell cultures using a pH-dependent dynamic model. J. Biosci. Bioeng. 2018, 125, 245–250. [Google Scholar] [CrossRef]
- Kappatou, C.D.; Altunok, O.; Mhamdi, A.; Mantalaris, A.; Mitsos, A. Sequential and simultaneous optimization strategies for increased production of monoclonal antibodies. Comput.-Aided Chem. Eng. 2019, 46, 1021–1026. [Google Scholar]
- Niu, D.; Jia, M.; Wang, F.; He, D. Optimization of nosiheptide fed-batch fermentation process based on hybrid model. Ind. Eng. Chem. Res. 2013, 52, 3373–3380. [Google Scholar] [CrossRef]
- Niu, D.; Zhang, L.; Wang, F. Modeling and parameter updating for nosiheptide fed-batch fermentation process. Ind. Eng. Chem. Res. 2016, 55, 8395–8402. [Google Scholar] [CrossRef]
- Rodman, A.D.; Gerogiorgis, D.I. Multi-objective process optimisation of beer fermentation via dynamic simulation. Food Bioprod. Process. 2016, 100, 255–274. [Google Scholar] [CrossRef] [Green Version]
- Rodman, A.D.; Gerogiorgis, D.I. Dynamic optimization of beer fermentation: Sensitivity analysis of attainable performance vs. product flavour constraints. Comput. Chem. Eng. 2017, 106, 582–595. [Google Scholar] [CrossRef]
- Biegler, L.T.; Cervantes, A.M.; Wächter, A. Advances in simultaneous strategies for dynamic process optimization. Chem. Eng. Sci. 2002, 57, 575–593. [Google Scholar] [CrossRef]
- Biegler, L.T. An overview of simultaneous strategies for dynamic optimization. Chem. Eng. Process. Process. Intensif. 2007, 46, 1043–1053. [Google Scholar] [CrossRef]
- Rodman, A.D.; Fraga, E.S.; Gerogiorgis, D.I. On the application of a nature-inspired stochastic evolutionary algorithm to constrained multi-objective beer fermentation optimisation. Comput. Chem. Eng. 2018, 108, 448–459. [Google Scholar] [CrossRef] [Green Version]
- Almeida, E.; Secchi, A.R. Dynamic optimization of a FCC converter unit: Numerical analysis. Braz. J. Chem. Eng. 2011, 28, 117–136. [Google Scholar] [CrossRef]
- Osorio, D.; Pérez-Correa, R.; Belancic, A.; Agosin, E. Rigorous dynamic modeling and simulation of wine distillations. Food Control 2004, 15, 515–521. [Google Scholar] [CrossRef]
- Farhat, S.; Czernicki, M.; Pibouleau, L.; Domenech, S. Optimization of multiple-fraction batch distillation by nonlinear programming. AIChE J. 1990, 36, 1349–1360. [Google Scholar] [CrossRef]
- Mujtaba, I.M.; Macchietto, S. Optimal operation of multicomponent batch distillation-multiperiod formulation and solution. Comput. Chem. Eng. 1993, 17, 1191–1207. [Google Scholar] [CrossRef]
- Sørensen, E.; Macchietto, S.; Stuart, G.; Skogestad, S. Optimal control and on-line operation of reactive batch distillation. Comput. Chem. Eng. 1996, 20, 1491–1498. [Google Scholar] [CrossRef]
- Cervantes, A.; Biegler, L.T. Large-scale DAE optimization using a simultaneous NLP formulation. AIChE J. 1998, 44, 1038–1050. [Google Scholar] [CrossRef]
- Cervantes, A.M.; Wächter, A.; Tütüncü, R.H.; Biegler, L.T. A reduced space interior point strategy for optimization of differential algebraic systems. Comput. Chem. Eng. 2000, 24, 39–51. [Google Scholar] [CrossRef]
- Logsdon, J.S.; Biegler, L.T. Accurate solution of differential-algebraic optimization problems. Ind. Eng. Chem. Res. 1989, 28, 1628–1639. [Google Scholar] [CrossRef]
- Tanartkit, P.; Biegler, L.T. Stable decomposition for dynamic optimization. Ind. Eng. Chem. Res. 1995, 34, 1253–1266. [Google Scholar] [CrossRef]
- Rodman, A.D.; Gerogiorgis, D.I. An investigation of initialisation strategies for dynamic temperature optimisation in beer fermentation. Comput. Chem. Eng. 2019, 124, 43–61. [Google Scholar] [CrossRef] [Green Version]















| Antibiotic | Application | Study | Reference |
|---|---|---|---|
| Amoxicillin | Tonsillitis Bronchitis Pneumonia Gonorrhea Sinus infections UTIs | Application of artificial neural networks (ANNs) to model complex reaction scheme for penicillin G acylase (PGA)-catalyzed synthesis | [12] |
| Inclusion of additional experimental data to improve ANN in reference [12] | [13] | ||
| Maximization of API formation vs. different operating conditions in either methanol/ethylene glycol as reaction solvents | [14] | ||
| Sensitivity analysis on previous ANN study [12] | [15] | ||
| Modeling and simulation of continuous reactive crystallization in presence of substrates and impurities | [16,17] | ||
| Dynamic optimization of non-isothermal batch reactor | [18] | ||
| Ampicillin | UTIs Pneumonia Gonorrhea Meningitis Abdominal infections | Regression of nucleation and growth kinetics for pH crystallization model | [19] |
| Modeling and simulation of reactive crystallization in presence of substrates and impurities | [20] | ||
| Modeling and simulation of continuous reactive crystallization in presence of substrates and impurities | [16,17] | ||
| Multi-objective dynamic optimization of pH crystallization | [21] | ||
| Cephalexin | UTIs Respiratory tract infections Ear infections Skin infections | Non-isothermal modeling of enzymatic cephalexin batch synthesis | [22] |
| Optimization of synthesis pH, temperature, and concentrations | [23] | ||
| Non-isothermal modeling of enzymatic cephalexin batch synthesis | [24] | ||
| Modeling and simulation of reactive crystallization in presence of substrates and impurities | [16,17] | ||
| Regression of nucleation and growth kinetics for pH crystallization model | [25] |
| Product | Biomass | Substrate | Objectives | Observations | Reference | ||
|---|---|---|---|---|---|---|---|
| Molecule | Application | ||||||
| 1 | Podophyllotoxin | Anticancer | Podophyllum hexandrum | Indoleacetic acid, glucose, oxygen | Regress model parameters from batch data to inform fed-batch design | Increased volumetric productivity by 35.8%. | [26] |
| 2 | Unnamed protein | Unknown | Unnamed | Glucose, oxygen | Application of ANNs to model bioprocess | ANN formulated to capture industrial process behavior. | [27] |
| 3 | Fluoroleucine ethyl ester | Pharmaceutical intermediate | Candida antarctica | Azlactone, ethanol | Kinetic parameter regression for fed-batch process optimization | 400% increase in fed-batch mode productivity vs. batch operation | [28] |
| 4 | Glutamine | Amino acid | CHO cells | Glucose, oxygen | Markov chain Monte Carlo method for kinetics modeling | Fed-batch process modeling in 5000 L bioreactor | [29] |
| 5 | Butyric acid | Histamine antagonist | Clostridium tyrobutyricum | Glucose, oxygen | Reaction kinetic model parameter regression for fed-batch process | Increased productivity and growth with fed-batch operation | [30] |
| 6 | Penicillin | Antibiotic | Penicillium | Glucose, oxygen | Implementation of design of dynamic experiments for process optimization | Process optimization with few experiments | [31] |
| 7 | mAb | Various therapeutic applications | GS-NS0 cell line | Glucose | Sensitivity analysis and dynamic optimization | Increased productivity | [32] |
| 8 | EG2-hFc (mAb) | Various therapeutic applications | CHO cells | Glucose, oxygen | Reaction kinetic parameter regression and sensitivity analysis | Single set of parameters described state trajectories | [33] |
| 9 | Unnamed mAb | Various therapeutic applications | CHO cells | Glucose, oxygen | Reaction kinetic parameter regression for modeling | System modeling on lab- and production scales | [34] |
| 10 | β-Carotene | Vitamin A precursor | Saccharomyces cerevisiae | Glucose, ethanol, oxygen | Dynamic optimization of reaction scheme | Reduced operating costs of bioreactor | [35] |
| 11 | mAb | Various therapeutic applications | GS-NS0 cells | Glucose, glutanamine | Model reformulation to improve computational efficiency | Improved structure and increased production from optimal feeding | [36] |
| 12 | Immunoglobulin G (mAb) | Various therapeutic applications | CHO cells | Unspecified | Dynamic model formulation for optimal pH control | Increased productivity from optimal control | [37] |
| 13 | mAb | Various therapeutic applications | GS-NS0 cells | Glucose, glutanamine | Comparison of simultaneous and sequential optimization | Sequential approach attains higher productivity | [38] |
| Kinetic Parameters | ||||
| Parameter Description | Symbol | Value | Units | Source |
| Growth pre-exponent | Ag | 0.1224 | h−1 | [40] |
| Growth energy barrier | Eg | 60 | kJ mol−1 | [40] |
| Death pre-exponent | Ad | 1.9 × 10−3 | h−1 | [40] |
| Death energy barrier | Ed | 340 | kJ mol−1 | [40] |
| Equation (2) constant | K1 | 1 × 10−10 | (–) | [40] |
| Equation (2) constant | K2 | 1.3 × 10−4 | (–) | [40] |
| Substrate Contois constant | KS | 0.1828 | g L−1 | [40] |
| Oxygen Contois constant | KO | 0.0352 | g L−1 | [40] |
| Maximum substrate concentration | XMAX | 0.87 | g L−1 | [40] |
| Monod constant | Kd | 0.0368 | (–) | [40] |
| Hydrolysis constant | Kh | 4.0 × 10−4 | h−1 | This study a |
| Substrate maintenance coefficient | mS | 0.0624 | g g−1 h−1 | [40] |
| Biomass/substrate yield constant | YX/S | 0.25 | g g−1 | [40] |
| Product/substrate yield constant | YP/S | 0.68 | g g−1 | [40] |
| Specific production rate | μP | 0.05 | g g−1 h−1 | This study a |
| Production inhibition constant | KI | 0.1 | g L−1 | [39] |
| Production inhibition constant | KP | 2 × 10−4 | g L−1 | [39] |
| Oxygen maintenance coefficient | mO | 4.0 × 10−3 | g g−1 h−1 | This study a |
| Biomass/oxygen yield constant | YX/O | 43.5 | g g−1 | This study a |
| Product/oxygen yield constant | YP/O | 253.3 | g g−1 | This study a |
| Design Parameters | ||||
| Parameter Description | Symbol | Value | Units | Source |
| Fermentor volume | VF | 100 | L | [39,40] |
| Ventilation rate | Q | 3.0 | m3 h−1 | [39,40] |
| Agitation speed | n | 400 | rpm | [39,40] |
| Stirring power | P | 1500 | W | [39,40] |
| Agitator diameter | d | 0.01 | m | [39,40] |
| Vessel diameter | D | 0.5 | m | [39,40] |
| a Quality of Parameter Fit: Niu et al. (2013, 2016) [39,40] vs. this study | ||||
| Variable | MSE | SSE | ||
| Niu et al. (2013, 2016) [39,40] | This study | Niu et al. (2013, 2016) [39,40] | This study | |
| Product, P | 4.940 × 10–1 | 6.815 × 10–5 | 8.398 | 1.158 × 10−3 |
| Dissolved Oxygen, CO | 3.700 × 103 | 4.280 × 10−5 | 6.290 × 104 | 0.728 × 10−3 |
| Operating Variable | |||
| Variable | Symbol | Initial Value | Units |
| Temperature | T(t0) = T(t) | 30 | °C |
| pH | pH(t0) = pH(t) | 7 | (–) |
| State Initial Condition | |||
| Variable | Symbol | Initial Value | Units |
| Biomass loading | X (t0) | 0.05 | g L−1 |
| Substrate concentration | S (t0) | 40 | g L−1 |
| Product concentration | P (t0) | 0 | g L−1 |
| Culture volume | V (t0) | 60 | L |
| Dissolved oxygen content | CO (t0) | 0.037 | g L−1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodman, A.D.; Diab, S.; Gerogiorgis, D.I. Dynamic Optimization of a Fed-Batch Nosiheptide Reactor. Processes 2020, 8, 587. https://doi.org/10.3390/pr8050587
Rodman AD, Diab S, Gerogiorgis DI. Dynamic Optimization of a Fed-Batch Nosiheptide Reactor. Processes. 2020; 8(5):587. https://doi.org/10.3390/pr8050587
Chicago/Turabian StyleRodman, Alistair D., Samir Diab, and Dimitrios I. Gerogiorgis. 2020. "Dynamic Optimization of a Fed-Batch Nosiheptide Reactor" Processes 8, no. 5: 587. https://doi.org/10.3390/pr8050587
APA StyleRodman, A. D., Diab, S., & Gerogiorgis, D. I. (2020). Dynamic Optimization of a Fed-Batch Nosiheptide Reactor. Processes, 8(5), 587. https://doi.org/10.3390/pr8050587