Population-Based Parameter Identification for Dynamical Models of Biological Networks with an Application to Saccharomyces cerevisiae

Abstract

One of the central elements in systems biology is the interaction between mathematical modeling and measured quantities. Typically, biological phenomena are represented as dynamical systems, and they are further analyzed and comprehended by identifying model parameters using experimental data. However, all model parameters cannot be found by gradient-based optimization methods by fitting the model to the experimental data due to the non-differentiable character of the problem. Here, we present POPI4SB, a Python-based framework for population-based parameter identification of dynamic models in systems biology. The code is built on top of PySCeS that provides an engine to run dynamic simulations. The idea behind the methodology is to provide a set of derivative-free optimization methods that utilize a population of candidate solutions to find a better solution iteratively. Additionally, we propose two surrogate-assisted population-based methods, namely, a combination of a k-nearest-neighbor regressor with the Reversible Differential Evolution and the Evolution of Distribution Algorithm, that speeds up convergence. We present the optimization framework on the example of the well-studied glycolytic pathway in Saccharomyces cerevisiae.

1. Introduction

Mathematical models in systems biology are mostly represented by ordinary differential equations (ODEs). They provide a representation of the information obtained from experimental observations about the structure and function of a particular biological network [1,2]. The integral component of ODEs is parameters that correspond to the kinetic characteristics of a reaction catalyzed by a specific enzyme in particular conditions. Typically, the parameters are identified by fitting the model to experimental data or are measured for individual reactions separately. Once parameter values are determined, dynamic models could be used to confirm hypotheses, draw predictions and find such (time-varying) stimulation conditions that result in a particular desired behavior of a system [2,3,4]. However, the problem of fitting a dynamical model to experimental data is non-differentiable, thus, derivative-free optimization methods should be used instead of gradient-based or higher-order optimizers [5,6].

Here, we present a framework that implements a set of population-based optimization methods to identify parameters in a dynamic model of a biological network of interest, from limited available experimental data. In other words, the presented framework allows finding parameter values of a dynamical model while only selected quantities are observed. This could drastically decrease the time of fitting separate reactions to data and improve estimation quality because all reactions are considered as a whole, thus, it takes into account interaction among reactions. The implementation of the approach is a stand-alone Python program. It utilizes PySCeS (Python Simulator for Cellular System) [7], a modeling tool for formulating dynamical models of biological networks and running simulations by solving ODEs numerically. Our framework loads a model developed using PySCeS or from the JWS database [8] together with experimental data, and outputs parameter values for which a difference between the experimental data and the simulation is smallest. Moreover, the framework allows adding new optimizers to a single file, without the necessity of changing any other parts of the program. Please see Supplementary Data for details. We refer to this framework as POPI4SB, see its schematic representation in Figure 1.

In this study, we chose glycolysis that is a crucial metabolic pathway and its upregulation is correlated with diseases like cancer [9,10]. Nearly all living organisms carry out glycolysis as a part of cellular metabolism. One of the most intensively studied organisms in the context of, among others, glycolysis is Saccharomyces cerevisiae species, also known as baker’s yeast [11,12,13,14,15]. We applied our optimization framework to a model of glycolysis in yeast proposed in [16]. This model contains lumped reactions of the glycolytic pathway and includes production of glycerol, fermentation to ethanol and exchange of acetaldehyde between the cells, and trapping of acetaldehyde by cyanide.

The contribution of the paper is threefold:

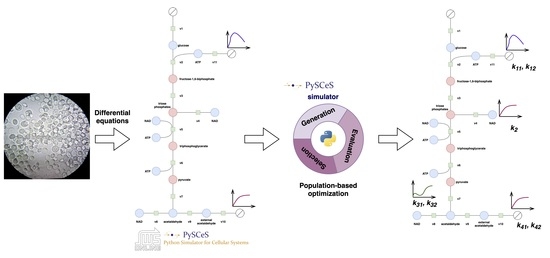
• We provide a population-based optimization framework for parameter identification and showcase its performance on the example of the glycolysis of Saccharomyces cerevisiae, one of the most studied species in biology.
• We analyze the performance of the population-based optimization framework in the considered problem and indicate its high potential for future research.
• We extend the Python framework PySCeS [7] by implementing the population-based optimization methods (four methods known in the literature, and two new methods) in Python. The code for the methods together with the experiments is available online: https://github.com/jmtomczak/popi4sb.

2. Materials and Methods

2.1. Derivative-Free Optimization

We consider an optimization problem of a function $f:\mathbb{X}\to \mathbb{R}$, where $\mathbb{X}\subseteq {\mathbb{R}}^D$ is the search space. In this paper we focus on the minimization problem, namely:

$${\mathbf{x}}^{*}=arg\underset{\mathbf{x}\in \mathbb{X}}{min}f(\mathbf{x};\mathcal{D}),$$

(1)

where $\mathcal{D}$ denotes observed data.

Further, we assume that the analytical form of the function f is unknown or cannot be used to calculate derivatives, however, we can query it through a simulation or experimental measurements. Problems of this sort are known as derivative-free or black-box (In general, a black-box problem means that a formal description of a problem is unknown, however, very often non-differentiable problems with known mathematical representation (e.g., differential equations) are treated as black-box) optimization problems [5,17]. Additionally, we consider a bounded search space, i.e., we include inequality constraints for all dimensions in the following form: $l_d\le x_d\le u_d$, where $l_d,u_d\in \mathbb{R}$ and $l_d<u_d$, for $d=1,2,\dots ,D$.

2.2. Population-Based Optimization Methods

One group of widely-used methods for derivative-free optimization problems is population-based optimization algorithms. The idea behind these methods is to use a population of individuals, i.e., a collection of candidate solutions $\mathcal{X}=\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N\}$, instead of a single individual in the iterative manner. The premise of utilizing the population over a single candidate solution is to obtain better exploration of the search space and exploiting potential local optima [18,19].

In the essence, every population-based algorithm consists of three following steps that utilize a procedure for generating new individuals G, and a selection procedure S, that is:

• (Init) Initialize $\mathcal{X}=\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N\}$ and evaluate all individuals ${\mathcal{F}}_x=\{f_n:f_n=f\left(x_n\right),$$x_n\in \mathcal{X}\}$.
• (Generation) Generate new candidate solutions using the current population, $\mathcal{C}=G(\mathcal{X},{\mathcal{F}}_x)$.
• (Evaluation) Evaluate all candidates solutions:

  $${\mathcal{F}}_c=\{f_n:f_n=f\left(x_n\right),x_n\in \mathcal{C}\}.$$
• (Selection) Select a new population using the candidate solutions and the old population

  $$\mathcal{X}:=S(\mathcal{X},{\mathcal{F}}_x,\mathcal{C},{\mathcal{F}}_c).$$
  Go to Generate or terminate.

An exemplary population-based optimization approach is depicted in Figure 2.

In general, the population-based optimization methods are favorable over standard derivative-free optimization (DFO) algorithms in problems when querying the objective function is relatively cheap. Their computational complexity depends mainly on the population size, i.e., it is linear with respect to the size of the population N. Other DFO methods are typically more expensive. Bayesian Optimization, for instance, is known to give a good performance, but its complexity typically scales cubically with respect to the number of queries [20]. Here, we take advantage of the very low execution time of running a simulator (the glycolysis model) and propose to use the population-based methods for the parameter identification task.

There are a plethora of population-based DFO algorithms [5,6,18,21,22], however, our goal is to verify whether this approach, in general, could be successfully used in the considered task. Therefore, we decide to choose four instances of a group of methods that are easy-to-use and are proven to work well in practice: evolutionary strategies (ES), differential evolution (DE), estimation of distribution algorithms (EDA), and recently proposed reversible differential evolution (RevDE). Moreover, we propose to enhance EDA and RevDE with a surrogate model to allow better exploration and speed up calculations.

2.2.1. Evolutionary Strategies (ES)

Evolutionary strategies can be seen as a specialization of evolutionary algorithms with very specific choices of G and S. The core of ES is to formulate G using the multivariate Gaussian distribution. Here, we follow the widely-used (1 + 1)-ES that generates a new candidate using the Gaussian mutation parameterized by $\sigma >0$, namely:

$${\mathbf{x}}^{\prime }=\mathbf{x}+\sigma ·\epsilon ,$$

(2)

where $\epsilon \sim \mathcal{N}(0,\mathrm{I})$, and $\mathcal{N}(0,\mathrm{I})$ denotes the Gaussian distribution with zero mean and the identity covariance matrix $\mathrm{I}$. Next, if the fitness value of ${\mathbf{x}}^{\prime }$ is smaller than the value of fitness function of $\mathbf{x}$, the new candidate is accepted and the old one is discarded.

The crucial element of this approach is determining the value of $\sigma$. In order to overcome possibly time-consuming hyperparameter search, the following adaptive procedure is proposed [21]:

$$\sigma :=\left\{\begin{array}{cc}\sigma ·c& \mathrm{if}{p}_s<1/5,\\ \sigma /c& \mathrm{if}{p}_s>1/5,\\ \sigma & \mathrm{if}{p}_s=1/5.\end{array}\right.$$

(3)

where $p_s$ is the number of accepted individuals of the offspring divided by the population size N, and c is equal $0.817$ following the recommendation in [23].

2.2.2. Differential Evolution (DE)

Differential evolution is another population-based method that is loosely based on the Nelder-Mead method [24,25]. A new candidate is generated by randomly picking a triple from the population, $({\mathbf{x}}_i,{\mathbf{x}}_j,{\mathbf{x}}_k)\in \mathcal{X}$, and then ${\mathbf{x}}_i$ is perturbed by adding a scaled difference between ${\mathbf{x}}_j$ and ${\mathbf{x}}_k$, that is:

$$\mathbf{y}={\mathbf{x}}_i+F({\mathbf{x}}_j-{\mathbf{x}}_k),$$

(4)

where $F\in (0,2]$ is the scaling factor. This operation could be seen as an adaptive mutation operator that is widely known as differential mutation [25].

Further, the authors of [24] proposed to sample a binary mask $\mathbf{m}\in {\{0,1\}}^D$ according to the Bernoulli distribution with probability $p=P(m_d=1)$ shared across all D dimensions, and calculate the final candidate according to the following formula:

$$\mathbf{v}=\mathbf{m}\odot \mathbf{y}+(1-\mathbf{m})\odot {\mathbf{x}}_i,$$

(5)

where ⊙ denotes the element-wise multiplication. In the evolutionary computation literature this operation is known as uniform crossover operator [18]. In this paper, we fix $p=0.9$ following general recommendations in literature [26] and use the uniform crossover in all methods.

The last component of a population-based method is a selection mechanism. There are multiple variants of selection [18], however, here we use the “survival of the fittest” approach, i.e., we combine the old population with the new one and select N candidates with highest fitness values, i.e., the deterministic $(\mu +\lambda )$ selection.

This variant of DE is referred to as “DE/rand/1/bin”, where rand stands for randomly selecting a base vector, 1 is for adding a single perturbation and bin denotes the uniform crossover. Sometimes it is called classic DE [25].

2.2.3. Reversible Differential Evolution (RevDE)

The mutation operator in DE perturbs candidates using other individuals in the population to generate a single new candidate. As a result, having too small population could limit exploration of the search space. In order to overcome this issue, a modification of DE was proposed that utilized all three individuals to generate three new points in the following manner [27]:

$$\begin{array}{cc}\hfill {\mathbf{y}}_1& =x_i+F({\mathbf{x}}_j-{\mathbf{x}}_k)\hfill \\ \hfill {\mathbf{y}}_2& =x_j+F({\mathbf{x}}_k-{\mathbf{y}}_1)\hfill \\ \hfill {\mathbf{y}}_3& =x_k+F({\mathbf{y}}_1-{\mathbf{y}}_2).\hfill \end{array}$$

(6)

New candidates ${\mathbf{y}}_1$ and ${\mathbf{y}}_2$ could be further used to calculate perturbations using points outside the population. This approach does not follow a typical construction of an EA where only evaluated candidates are mutated. Further, we can express (6) as a linear transformation using matrix notation by introducing matrices as follows:

$$\left[\begin{array}{c}{\mathbf{y}}_1\\ {\mathbf{y}}_2\\ {\mathbf{y}}_3\end{array}\right]=\underset{=\mathbf{R}}{\underbrace{\left[\begin{array}{ccc}1& F& -F\\ -F& 1-F^2& F+F^2\\ F+F^2& -F+F^2+F^3& 1-2F^2-F^3\end{array}\right]}}\left[\begin{array}{c}{\mathbf{x}}_1\\ {\mathbf{x}}_2\\ {\mathbf{x}}_3\end{array}\right].$$

(7)

In order to obtain the matrix $\mathbf{R}$, we need to plug ${\mathbf{y}}_1$ to the second and third equation in (6), and then ${\mathbf{y}}_2$ to the last equation in (6). As a result, we obtain $M=3N$ new candidate solutions. This version of DE is called Reversible Differential Evolution, because the linear transformation $\mathbf{R}$ is reversible [27].

2.2.4. Estimation of Distribution Algorithms (EDA)

Most of the population-based optimization methods aim at finding a solution and the information about the distribution of the search space and the fitness function is represented implicitly by the population. However, this distribution could be modeled explicitly using a probabilistic model [19]. These methods have become known as the estimation of distribution algorithms [28,29,30].

The key difference between EDA and EA is the generation step. While an EA uses evolutionary operators like mutation and cross-over to generate new candidate solutions, EDA fits a probabilistic model to the population, and then new individuals are sampled from this model.

Therefore, fitting a distribution to the population is the crucial part of an EDA. There are various probabilistic models that could be used for this purpose. Here, we propose to fit the multivariate Gaussian distribution $\mathcal{N}(\mu ,\Sigma )$ to the population $\mathcal{X}$. For this purpose, we can use the empirical mean and the empirical covariance matrix:

$$\widehat{\mu }=\frac{1}{N}\sum _{n=1}^N{\mathbf{x}}_n,$$

(8)

and

$$\widehat{\Sigma }=\frac{1}{N}\sum _{n=1}^N({\mathbf{x}}_n-\widehat{\mu }){({\mathbf{x}}_n-\widehat{\mu })}^{\top }.$$

(9)

An efficient manner of sampling new candidates is to first calculate the Cholesky decomposition of the covariance matrix, $\widehat{\Sigma }=\mathbf{L}{\mathbf{L}}^{\top }$, where $\mathbf{L}$ is the lower-triangular matrix, and then computing:

$${\mathbf{x}}^{\prime }=\widehat{\mu }+\mathbf{L}\epsilon ,$$

(10)

where $\epsilon \sim \mathcal{N}(0,\mathrm{I})$. The Equation (10) is repeated M times to generate a new set of candidate solutions. Here, we set M to the size of the population, i.e., $M=N$. Once new candidate solutions are generated, the selection mechanism is applied. In this paper, we use the same selection procedure as the one used for DE.

2.2.5. Population-Based Methods with Surrogate Models (RevDE+ & EDA+)

Surrogate models: A possible drawback of population-based methods is the necessity of evaluating large populations that, even though we assume a low time cost per a single evaluation, could significantly slow down the whole optimization process. To overcome this issue, a surrogate model could be used to partially replace querying the fitness function  [31]. The surrogate model is either a probabilistic model or a machine learning model (e.g., a neural network) that gathers previously evaluated populations and allows to mimic the behavior of the fitness function. While applying the surrogate model, it is assumed that its utilization cost (e.g., training) is lower or even significantly lower than the computational cost of running the simulator.

There are multiple possible surrogate models, however, non-parametric models, e.g., Gaussian processes [20], are preferable, because they do not suffer from catastrophic forgetting (i.e., overfitting to the last population and forgetting first populations). Here, we consider another non-parametric model, namely, K-Nearest-Neighbor (K-NN) regression model that stores all previously seen individuals with evaluations, and the prediction of a new candidate solution is an average over K (e.g., $K=3$) closest previously seen individuals. Current implementations of the K-NN regressor provide efficient search procedures that result in the computational complexity better than $N·D$, e.g., using KD-trees results in $O(DlogN)$. This computational complexity is significantly better than the computational complexity of Gaussian processes, $O\left(N^3\right)$.

RevDE+: In the RevDE approach, we generate $3N$ new candidate solutions and all of them are further evaluated. However, this introduces an extra computational cost of running the simulator. This issue could be alleviated by using the K-NN regressor to approximate the fitness values of the new candidates. Further, we can select N most promising points. We refer to this approach as RevDE+.

EDA+: The outlined procedure of EDA produces M new candidate solutions and to keep a similar computational cost as ES and DE, we set M to N. However, this could significantly limit the potential of modeling a search space, because sampling in high-dimensional search spaces requires a significantly large number of points. A potential solution to this problem could be the application of the K-NN regressor to quickly verify the L new points. As long as the time cost of providing the approximated value of the fitness function is lower than the running time of the simulator, we can afford to take $L>N$ (e.g., $L=5N$). We refer to this approach as EDA+.

2.3. The Model of Glycolysis in Saccharomyces Cerevisiae

Introduction: As an example, we chose glycolysis that is a crucial metabolic pathway and its upregulation is correlated with diseases like cancer [9,10]. Nearly all living organisms carry out glycolysis as a part of cellular metabolism. A glycolytic path that consists of a series of reactions breaks down glucose into two three-carbon compounds and extracts energy for cellular metabolism. Therefore, glycolysis is at the heart of classical biochemistry and, as such, it is very well described. One of the most intensively studied organisms in the context of, among others, glycolysis is Saccharomyces cerevisiae species, also known as baker’s yeast [11,12,13,14,15]. Whereas, the dynamic model of glycolysis in Saccharomyces cerevisiae is of big interest in systems biology dynamic modeling literature [16,32,33,34,35].

We applied our optimization framework to a model of glycolysis in yeast proposed in [16], see Figure 3, that suffices to present the essence of our framework. This model contains lumped reactions of the glycolytic pathway and includes the production of glycerol, fermentation to ethanol, and exchange of acetaldehyde between the cells, and trapping of acetaldehyde by cyanide.

A system of Ordinary Differential Equations: In the considered model of the glycolysis we distinguish the following metabolites: glycolysis (glu), fructose-1,6-bisphosphate (fru), triosephosphates (triop), triphosphoglycerate (tp), pyruvate (pyr), acetaldehyde (ac), external acetaldehyde (ace).

Following the same assumptions as in [16] (i.e., a homogeneous distribution of the metabolites in the intracellular and in the extracellular solution), the system of ordinary differential equations of the glycolysis model in Saccharomyces cerevisiae is the following [36]:

$$\begin{array}{cc}\hfill \dot{glu}& =v_1-v_2\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \dot{fru}& =v_2-v_3\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \dot{triop}& =2v_3-v_4-v_5\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \dot{tp}& =v_5-v_6\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill \dot{pyr}& =v_6-v_7\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \dot{ac}& =v_7-v_8-v_9\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \dot{ace}& =0.1v_9-v_{10}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \dot{atp}& =-2v_2+v_5+v_6-v_{11}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \dot{nad}& =v_4-v_5-v_8\hfill \end{array}$$

(19)

with the rate equations:

$$\begin{array}{cc}\hfill v_1& =k_0\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill v_2& =\frac{k_1·glu·at}{1+{(at/k_i)}^n}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill v_3& =k_2·fru\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill v_4& =\frac{k_{31}·k_{32}·triop·nadA-k_{33}·k_{34}·tp·atpN}{k_{33}·N+k_{32}·A}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill v_5& =k_4·tp·A\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill v_6& =k_5·pyr\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill v_7& =k_6·ac·nad\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill v_8& =k_7·atp\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill v_9& =k_8·triop·nad\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill v_{10}& =k_9·ace\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill v_{11}& =k_7·atp\hfill \end{array}$$

(30)

where $A=\left(a_{tot}-atp\right)$ and $N=\left(n_{tot}-nad\right)$.

• Initial conditions

The initial conditions are the following:

$atp=2.0$	$nad=0.6$	$glu=5.0$
$fru=5.0$	$triop=0.6$	$tp=0.7$
$pyr=8.0$	$ac=0.08$	$ace=0.02$.

• Real parameter values

The real values of the parameters are the following [36]:

$a_{tot}=4\in [0,10]$	$k_0=0\in [0,10]$	$k_1=550\in [550,600]$
$k_2=9.8\in [0,10]$	$k_{31}=323.8\in [300,350]$	$k_{32}=\mathrm{76,411.1}\in [\mathrm{76,400},\mathrm{76,450}\mathrm{}]$
$k_{33}=\mathrm{57,823.1}\in [\mathrm{57,800},\mathrm{57,850}]$	$k_{34}=23.7\in [20,50]$	$k_4=80\in [80,100]$
$k_5=9.7\in [0,10]$	$k_6=2000\in [2000,2050]$	$k_7=28.0\in [20,50]$
$k_8=85.7\in [80,100]$	$k_9=0\in [0,10]$	$k_{10}=375\in [350,400]$
$k_i=1\in [0,10]$	$n=4\in [0,10]$	$n_{tot}=1\in [0,10]$

where we indicate the set of possible values of the parameters in the square brackets.

We note that for the sake of our experiments, we set $k_0$ to 0 (originally: $k_0=50$ [36]) in order to forbid a constant injection of $glu$, and $k_9$ to 0 (originally: $k_9=80$ [36]) in order to avoid oscillatory behavior of the system.

3. Experimental Setup

The experiments have been carried in  silico in which the performance of the selected algorithms has been evaluated.

3.1. Implementation

POPI4SB is implemented in Python, and utilizes PySCeS for running simulations. The code for carrying out experiments is available online: https://github.com/jmtomczak/popi4sb. The list of requirements is provided therein.

3.2. Parameter Identification & the Fitness Function

We consider the glycolysis process in yeast as a biochemical system with inputs and outputs (see Figure 3). The input to the system is glucose (glu), and the outputs are ATP (atp), NAD (nad), acetaldehyde (ac), and external acetaldehyde (ace). The other metabolites, i.e., triose phosphates (triop), pyruvate (pyr), fructose-1,6-biphosphate (fru) and triphosphoglycerate (tp) are considered to be unobserved quantities. The system is governed by 11 reactions with 18 parameters in total (see Appendix for details). Each reaction is represented by an ordinary differential equation that is known. We assume that we have inputs and outputs, namely, i.e., glu, atp, nad, ac, and ace, and each quantity is represented as a timecourse of length T. We denote these measurements by

$$\mathcal{D}=\{\mathit{glu},\mathit{atp},\mathit{nad},\mathit{ac},\mathit{ace}\}.$$

Further, following the nomenclature presented in [37], we consider the system of differential equations representing the glycolysis process as the simulator that for given values of parameters and initial conditions provides timecourses of all metabolites. Then, we can denote parameters by $\mathbf{x}$ and the simulator by $\mathrm{sim}:\mathcal{X}\to {\mathbb{R}}^{9\times T}$, i.e., $\mathrm{sim}$ takes parameters $\mathbf{x}$ and simulates timcourses of length T for all 9 metabolites, including $\mathit{glu},\mathit{atp},\mathit{nad},\mathit{ac},\mathit{ace}$. In order to calculate the objective (or the fitness) of the parameter values, we use the following function:

$$f(\mathbf{x};\mathcal{D})=\sum _{i=1}^5\frac{1}{\gamma ·T}\sum _{t=1}^T{\parallel {\mathbf{y}}_{i,t}-{\mathrm{sim}}_{i,t}\left(\mathbf{x}\right)\parallel }_2^2,$$

(31)

where ${\mathbf{y}}_{i,t}$ corresponds to one of the five observed metabolites at the t-th time step, and ${\mathrm{sim}}_{i,t}\left(\mathbf{x}\right)$ is the corresponding synthetically generated signal given by the simulator with parameters $\mathbf{x}$, $\gamma >0$ specifies the strength of penalizing a mistake. Notice that this is the (unnormalized) logarithm of the product of Gaussian distributions with means given by $\mathrm{sim}\left(\mathbf{x}\right)$ and the diagonal covariance matrix with shared variance $\gamma$.

3.3. Simulated Data

In the experiments, we assume that glu, atp, nad, ac, and ace are observed. We generate the observed metabolites by running the simulator with the real parameter values. To mimic real measurements that are typically noisy, we add a Gaussian noise with zero mean and the standard deviation equal $3\%$ of a generated value of a metabolite at a given time step. Adding noise prohibits finding a solution (i.e., values of parameters) that achieves error defined in Equation (31) equal zero. We repeat all experiments three times. For each repetition, we set the length of a timecourse to $T=30$.

3.4. Settings

For all optimization methods, we set the population size to $N=100$. All optimizers run maximally 1000 generations. In the case of ES, we use the initial value of $\sigma$ equal $0.1$. For DE, RevDE, and RevDE+, we use $F=0.5$, and $p=0.9$. For EDA we take $M=100$. In the case of EDA+ and RevDE+, we use the K-NN as the surrogate model with $K=3$, and we do not store more than 10,000 evaluated individuals.

4. Results & Discussion

Fitness value: In Figure 4 we present convergence of the methods in Figure 4. We notice that all methods were able to converge and achieve very similar fitness values. However, the (1 + 1)-ES method was slowest due to the slow exploration capabilities. EDA also required more evaluations to obtain better results. Interestingly, DE, RevDE, RevDE+, and EDA+ achieved almost identical values of the fitness function (the differences were beyond the three-digit precision). An important observation is that application of the surrogate model (the K-NN regressor) allowed to significantly speed up the convergence of RevDE+ and EDA+ compared to RevDE and EDA, respectively. We conclude that all population-based methods were able to converge and achieved almost identical scores, and our proposition of applying the surrogate model led to improving both RevDE and EDA.

Timecourses: The final value of the fitness function tells us how well the simulator models the observed timecourses for given parameters provided by an optimizer. Additionally, we can also qualitatively inspect the timecourses both the observed and unobserved metabolites. In Figure 5 we present timecourses for the unobserved metabolites, for parameter values found the five methods.

For all unobserved metabolites, the average over 3 repetitions of the experiments overlapped with the real value or laid within the confidence interval ($3\times$ standard deviation). This is a result that we hoped for since being able to generate unobserved metabolite is extremely important for analyzing biological systems. However, we notice that DE and RevDE+ led to almost identical timecourses, thus, they were able to properly identify  parameters.

Differences in parameters: In this paper, we know precisely the values of the parameters since they were measured in [16]. Hence, we can compare the parameter values found by the optimization methods with the real parameter values. We use the absolute value of the difference of two values. We calculate the mean and the standard deviations of the difference from three runs, and use the cumulative distribution function of the folded normal distribution to visualize the distribution of differences (the ideal case is 0). The difference between two real-valued random variable is normally distributed. However, taking the absolute value of a normally distributed random variable results in the folded normal distribution.

In Figure 6 we present difference of all parameters. In general, the differences are marginal and we can conclude that all parameter values were rather properly identified. The biggest problems though appear for parameters that have very large values, e.g., $k_8$ or $k_{33}$. This result is very promising because it seems to confirm the promise of the paper that it is possible to identify parameters of a complex biological network for only partially observable metabolites.

5. Conclusions

In this work, we present a population-based framework for parameter identification of biological networks described as dynamic models. The obtained results indicate the great potential of population-based optimization methods in the field of biology and biochemistry. In the case of relatively low computational costs of obtaining an evaluation of parameters, the population-based methods seem to be sufficient to solve the parameter identification problem. Moreover, our results for applying surrogate models to the optimizers can be highly effective (i.e., speeding up convergence). It is a known fact (e.g., see [31,38]), nevertheless, we believe that the optimization with surrogate models has a great future and should be further investigated. For instance, considering other classes of surrogate models like Gaussian processes or (Bayesian) neural networks opens new opportunities and research questions worth following.

Additionally, the development of our framework in Python, an open-source platform, simplifies its distribution and enables its use on most operating systems. POPI4SB is easy-to-use and since the code is freely available, it constitutes a platform for developing new population-based optimizers. Therefore, the proposed framework can be relatively easily extended and serve for future research.