Cobalt Biosorption in Fixed-Bed Column Using Greenhouse Crop Residue as Natural Sorbent
Abstract
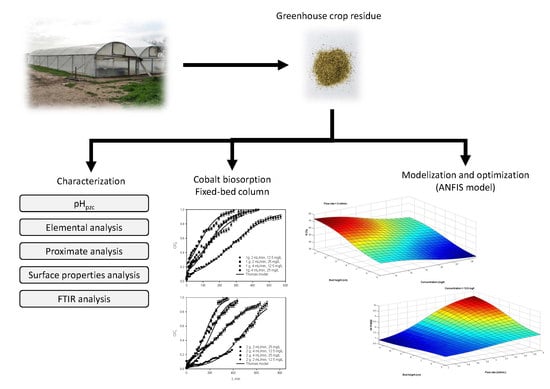
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Column Biosorption Tests
2.3. Optimization of the Operating Conditions in Continuous Biosorption by ANFIS Model
3. Results and Discussion
3.1. Column Biosorption Tests
3.2. Optimization of Operating Conditions in Continuous Biosorption Using ANFIS Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hossain, M.A.; Ngo, N.N.; Guo, W.S.; Nguyen, T.V.; Vigneswaran, S. Performance of cabbage and cauliflower wastes for heavy metals removal. Desalin. Water Treat. 2014, 52, 844–860. [Google Scholar] [CrossRef]
- Abdolali, A.; Ngo, H.H.; Guo, W.; Zhou, J.L.; Zhang, J.; Liang, S.; Chang, S.W.; Nguyen, D.D.; Liu, Y. Application of a breakthrough biosorbent for removing heavy metals from synthetic and real wastewaters in a lab-scale continuous fixed-bed column. Bioresour. Technol. 2017, 229, 78–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cárdenas, J.F.; Rodríguez, A.S.; Vargas, J.M.; Martínez, V.M.; Acosta, I.; Michel, C.; Gallegos, F.; Escalera, M.E.; Muñoz, A. Bioremoval of Cobalt(II) from Aqueous Solution by Three Different and Resistant Fungal Biomasses. Bioinorg. Chem. Appl. 2019, 2019, 8757149. [Google Scholar] [CrossRef] [PubMed]
- Lauwerys, R.; Lison, D. Health risks associated with cobalt exposure-an overview. Sci Total Env. 1994, 150, 1–6. [Google Scholar] [CrossRef]
- Khan Rao, R.A.; Khatoon, A. Aluminate treated Casuarina equisetifolia leaves as potential adsorbent for sequestering Cu(II), Pb(II) and Ni(II) from aqueous solution. J. Clean. Prod. 2017, 165, 1280–1295. [Google Scholar] [CrossRef]
- Chai, W.S.; Cheun, J.Y.; Jumar, P.S.; Mubashir, M.; Majeed, Z.; Banar, F.; Ho, S.-H.; Show, P.L. A review on conventional and novel materials towards heavy metal adsorption in wastewater treatment application. J. Clean. Prod. 2021, 296, 126589. [Google Scholar] [CrossRef]
- Yelatontsev, D. Production of versatile biosorbent via eco-friendly utilization of non-wood biomass. Chem. Eng. J. 2023, 451, 13881. [Google Scholar] [CrossRef]
- Quyen, V.T.; Pham, T.-H.; Kim, J.; Thanh, D.M.; Thang, P.Q.; Le, Q.V.; Jung, S.H.; Kim, T. Biosorbent derived from coffee husk for efficient removal of toxic heavy metals from wastewater. Chemosphere 2021, 284, 131312. [Google Scholar] [CrossRef]
- Martín-Lara, M.A.; Blázquez, G.; Calero, M.; Almendros, A.I.; Ronda, A. Binary biosorption of copper and lead onto pine cone shell in batch reactors and in fixed bed columns. Int. J. Miner. Process. 2016, 148, 72–82. [Google Scholar] [CrossRef]
- Calero, M.; Iáñez-Rodríguez, I.; Pérez, A.; Martín-Lara, M.A.; Blázquez, G. Neural fuzzy modelization of copper removal from wáter by biosorption in fixed-bed columns using olive stone a pinion shell. Bioresour. Technol. 2018, 252, 100–109. [Google Scholar] [CrossRef]
- Ahmadi, H.; Hafiz, S.S.; Sharifi, H.; Rene, N.N.; Habibi, S.S.; Hussain, S. Low cost biosorbent (Melon Peel) for effective removal of Cu (II), Cd (II), and Pb (II) ions from aqueous solution. Engineering 2022, 6, 100242. [Google Scholar] [CrossRef]
- Sankaran, R.; Show, P.L.; Ooi, C.-W.; Ling, T.C.; Shu-Jen, C.; Chen, S.-Y.; Chang, Y.-K. Feasibility assessment of removal of heavy metals and soluble microbial products from aqueous solutions using eggshell wastes. Clean Technol. Environ. Policy 2020, 22, 773–786. [Google Scholar] [CrossRef]
- Kamarudzaman, A.I.; Adan, S.N.A.C.; Hassan, Z.; Wahab, M.A.; Makhtar, S.M.Z.; Seman, N.A.A.; Jalil, M.F.A.; Handayani, D.; Syafiuddin, A. Biosorption of Copper(II) and Iron(II) using Spent Mushroom Compost as Biosorbent. Biointerface Res. Appl. Chem. 2022, 12, 7775–7786. [Google Scholar]
- Abdi, O.; Kazemi, M. A review study of biosorption of heavy metals and comparison between different biosorbents. J. Mater. Environ. Sci. 2015, 6, 1386–1399. [Google Scholar]
- Morosanu, I.; Teodosiu, C.; Paduraru, C.; Ibanescu, D.; Tofan, L. Biosorption of lead ions from aqueous effluents by rapeseed biomass. New Biotechnol. 2017, 39, 110–124. [Google Scholar] [CrossRef] [PubMed]
- Ronda, A.; Martín-Lara, M.A.; Almendros, A.I.; Pérez, A.; Blázquez, G. Comparison of two models for the biosorption of Pb (II) using untreated and chemically treated olive stone: Experimental design methodology and adaptive neural fuzzy inference system (ANFIS). J. Taiwan Inst. Chem. Eng. 2015, 54, 45–56. [Google Scholar] [CrossRef]
- Fawzy, M.; Nasr, M.; Adel, S.; Nagy, H.; Helmi, S. Environmental approach and artificial intelligence for Ni (II) and Cd (II) biosorption form aqueous solution using Typha domingensis biomass. Ecol. Eng. 2016, 95, 743–752. [Google Scholar] [CrossRef]
- Fawzy, M.; Nasr, M.; Helmi, S.; Nagy, H. Experimental and theoretical approaches for Cd (II) biosorption from aqueous solution using Oryza sativa biomass. Int. J. Phytoremediat. 2016, 18, 1096–1103. [Google Scholar] [CrossRef]
- Bingöl, D.; Inal, M.; Çetintaş, S. Evaluation of copper biosorption onto date palm (Phoenix dactylifera L.) seeds with MLR and ANFIS models. Ind. Eng. Chem. Res. 2013, 52, 4429–4435. [Google Scholar] [CrossRef]
- Jiménez, L.; Pérez, A.; de la Torre, M.J.; Rodríguez, A.; Angulo, V. Ethyleneglycol pulp from tagasaste. Bioresour. Technol. 2008, 99, 2170–2176. [Google Scholar] [CrossRef]
- Iáñez-Rodríguez, I.; Martín-Lara, M.A.; Blázquez, G.; Pérez, A.; Calero, M. Effect of torrefaction conditions on greenhouse crop residue: Optimization of conditions to upgrade solid characteristics. Bioresour. Tecnol. 2017, 244, 741–749. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Ali, S.S.; Hossain, S.S.; Asif, M. A review of the dynamic mathematical modeling of heavy metal removal with the biosorption process. Processes 2022, 10, 1154. [Google Scholar] [CrossRef]
- Chen, S.; Yue, Q.; Gao, B.; Li, Q.; Xu, X.; Fu, K. Adsorption of hexavalent chromium from aqueous solution by modified corn stalk: A fixed-bed column study. Bioresour. Technol. 2012, 113, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Sheng, L.; Zhang, Y.; Tang, F.; Liu, S. Mesoporous/microporous silica materials: Preparation from natural sands and highly efficient fixed-bed adsorption of methylene blue in wastewater. Microporous Mesoporous Mater. 2018, 257, 9–18. [Google Scholar] [CrossRef]
- Amin, M.T.; Alazba, A.A.; Shafiq, M. Batch and fixed-bed column studies for the biosorption of Cu(II) and Pb(II) by raw and treated date palm leaves and orange peel. Glob. NEST J. 2017, 19, 464–478. [Google Scholar]
- Hymavathi, D.; Prabhakar, G. Modeling of cobalt and lead adsorption by Ficusbenghalenesis L in a fixed bed column. Chem. Eng. Commun. 2019, 206, 1264–1272. [Google Scholar] [CrossRef]
- Rusu, L.; Grigoras, C.-G.; Simion, A.-I.; Suceveanu, E.-M.; Botezatu, A.V.D.; Harja, M. Biosorptive Removal of Ethacridine Lactate from Aqueous Solutions by Saccharomyces pastorianus Residual Biomass/Calcium Alginate Composite Beads: Fixed-Bed Column Study. Materials 2022, 15, 4657. [Google Scholar] [CrossRef]
- Yahya, M.D.; Abubakar, H.; Obayomi, K.S.; Iyaka, Y.A.; Suleiman, B. Simultaneous and continuous biosorption of Cr and Cu (II) ions from industrial tannery effluent using almond shell in a fixed bed column. Results Eng. 2020, 6, 100113. [Google Scholar] [CrossRef]
- Homem, N.C.; Vieira, A.M.S.; Bergamasco, R.; Vieira, M.F. Low-cost biosorbent based on Moringa oleifera residues for herbicide atrazine removal in a fixed-bed column. Can. J. Chem. Eng. 2018, 96, 1468–1478. [Google Scholar] [CrossRef]
- Hanumanthu, J.R.; Ravindiran, G.; Subramanian, R.; Saravanan, P. Optimization of process conditions using RSM and ANFIS for the removal of Remazol Brilliant Orange 3R in a packed bed column. J. Indian Chem. Soc. 2021, 98, 100086. [Google Scholar] [CrossRef]
- Parsaei, M.; Roudbari, E.; Piri, F.; El-Shafay, A.S.; Su, C.-H.; Nguyen, H.C.; Alashwa, M.; Ghazali, S.; Algarni, M. Neural-based modeling adsorption capacity of metal organic framework materials with application in wastewater treatment. Sci. Rep. 2022, 12, 4125. [Google Scholar] [CrossRef] [PubMed]
- Solanki, S.; Sinha, S.; Bisaria, K.; Singh, R.; Saxena, R. Accurate data prediction by fuzzy inference model for adsorption of hazardous azo dyes by novel algal doped magnetic chitosan bionanocomposite. Environ. Res. 2022, 214, 113844. [Google Scholar] [CrossRef] [PubMed]
- Dolatabadi, M.; Mehrabpour, M.; Esfandayari, M.; Alidadi, H.; Davoudi, M. Modeling of simultaneous adsorption of dye and metal ion by sawdust from aqueous solution using of ANN and ANFIS. Chemom. Intell. Lab. Syst. 2018, 181, 72–78. [Google Scholar] [CrossRef]










| Analysis | Value | |
|---|---|---|
| pHpzc | 7.35 | |
| Elemental analysis | %C | 34.02 |
| %H | 5.89 | |
| %N | 3.15 | |
| %O (by difference considering ash content) | 32.95 | |
| Immediate or proximate analysis | Moisture, % | 7.43 |
| Volatile matter, % | 56.66 | |
| Fixed carbon, % | 11.95 | |
| Ash, % | 23.97 | |
| Surface properties analysis | BET surface area, m2/g | 6.2 |
| Pore volume, cm3/g | 0.0073 | |
| Average pore size, Ǻ | 47.5 | |
| FTIR analysis | –OH (3330 cm−1) CH– (2760 y 2980 cm−1) C=O (1730 cm−1) Aromatic vibration of lignin (1620 cm−1) Functional groups located in lignin (1509 y 1200 cm−1) | |
| Bed Height, cm | Feed-flow Rate, mL/min | Inlet Cobalt Concentration, mg/L | %R | qtotal, mg | mtotal, mg | Vef, mL | qeq, mg/g | Ceq, mg/L | tS, min |
|---|---|---|---|---|---|---|---|---|---|
| 5 (1 g) | 2 | 25 | 31.6 | 7.3 | 23.1 | 870 | 7.3 | 18.2 | 435 |
| 12.5 | 47.8 | 7.3 | 15.2 | 1140 | 7.3 | 7.0 | 570 | ||
| 4 | 25 | 30.0 | 9.1 | 30.4 | 1140 | 9.1 | 18.7 | 285 | |
| 12.5 | 39.5 | 7.9 | 20.0 | 1380 | 7.9 | 8.7 | 345 | ||
| 11.5 (2 g) | 2 | 25 | 50.1 | 11.5 | 23.0 | 870 | 5.8 | 13.2 | 435 |
| 12.5 | 73.7 | 13.7 | 18.6 | 1380 | 6.9 | 1.8 | 690 | ||
| 4 | 25 | 43.5 | 17.0 | 39.1 | 1440 | 8.6 | 11.8 | 360 | |
| 12.5 | 52.7 | 19.1 | 36.9 | 2520 | 9.5 | 7.1 | 630 |
| Bed Height, cm | Feed-flow Rate, mL/min | Inlet Cobalt Concentration, mg/L | kTh, mL/mg/min | q0, mg/g | R2 | Σ(qexp − qcal)2 |
|---|---|---|---|---|---|---|
| 5 (1 g) | 2 | 25 | 0.54 | 6.7 | 0.990 | 0.032 |
| 12.5 | 0.64 | 7.2 | 0.995 | 0.017 | ||
| 4 | 25 | 0.63 | 7.4 | 0.953 | 0.092 | |
| 12.5 | 0.76 | 7.6 | 0.961 | 0.082 | ||
| 11.5 (2 g) | 2 | 25 | 0.55 | 5.7 | 0.989 | 0.045 |
| 12.5 | 0.60 | 6.6 | 0.985 | 0.061 | ||
| 4 | 25 | 0.61 | 8.5 | 0.992 | 0.027 | |
| 12.5 | 0.68 | 8.9 | 0.990 | 0.038 |
| Constant | %R | qe |
|---|---|---|
| a1 | 46.38 | 7.267 |
| a2 | 76.17 | 6.719 |
| a3 | 28.83 | 7.229 |
| a4 | 49.09 | 5.403 |
| a5 | 37.18 | 7.805 |
| a6 | 46.01 | 9.891 |
| a7 | 16.91 | 8.831 |
| a8 | 53.40 | 8.349 |
| Variable | Level | X | L | ||
|---|---|---|---|---|---|
| %R | qe | %R | qe | ||
| Feed-flow rate | Low | 2.180 | 1.993 | 1.1900 | 0.8330 |
| Feed-flow rate | High | 4.089 | 3.995 | 0.6425 | 0.8607 |
| Concentration | Low | 12.52 | 12.50 | 5.3590 | 5.3090 |
| Concentration | High | 25.04 | 25.00 | 5.2180 | 5.3080 |
| Bed-height | Low | 4.900 | 5.000 | 2.5140 | 2.7600 |
| Bed-height | High | 11.43 | 11.50 | 2.9180 | 2.7600 |
| %R | qe | ||||
|---|---|---|---|---|---|
| Experimental | Calculated | Error (%) | Experimental | Calculated | Error (%) |
| 31.56 | 31.56 | 0.003 | 7.29 | 7.290 | 0.003 |
| 47.77 | 47.77 | 0.010 | 7.28 | 7.280 | 0.005 |
| 30.01 | 30.01 | 0.006 | 9.13 | 9.129 | 0.013 |
| 39.54 | 39.54 | 0.008 | 7.94 | 7.940 | 0.002 |
| 50.14 | 50.14 | 0.003 | 5.77 | 5.769 | 0.011 |
| 73.69 | 73.69 | 0.007 | 6.87 | 6.870 | 0.004 |
| 43.45 | 43.45 | 0.004 | 8.59 | 8.593 | 0.205 |
| 52.71 | 52.71 | 0.007 | 9.53 | 9.529 | 0.011 |
| R2 > 0.999 | R2 > 0.999 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez, G.; Martín-Lara, M.Á.; Iáñez-Rodríguez, I.; Morales, I.; Pérez, A.; Calero, M. Cobalt Biosorption in Fixed-Bed Column Using Greenhouse Crop Residue as Natural Sorbent. Separations 2022, 9, 316. https://doi.org/10.3390/separations9100316
Blázquez G, Martín-Lara MÁ, Iáñez-Rodríguez I, Morales I, Pérez A, Calero M. Cobalt Biosorption in Fixed-Bed Column Using Greenhouse Crop Residue as Natural Sorbent. Separations. 2022; 9(10):316. https://doi.org/10.3390/separations9100316
Chicago/Turabian StyleBlázquez, Gabriel, María Ángeles Martín-Lara, Irene Iáñez-Rodríguez, Inés Morales, Antonio Pérez, and Mónica Calero. 2022. "Cobalt Biosorption in Fixed-Bed Column Using Greenhouse Crop Residue as Natural Sorbent" Separations 9, no. 10: 316. https://doi.org/10.3390/separations9100316
APA StyleBlázquez, G., Martín-Lara, M. Á., Iáñez-Rodríguez, I., Morales, I., Pérez, A., & Calero, M. (2022). Cobalt Biosorption in Fixed-Bed Column Using Greenhouse Crop Residue as Natural Sorbent. Separations, 9(10), 316. https://doi.org/10.3390/separations9100316