FEM Simulation of Frequency-Selective Surface Based on Thermoelectric Bi-Sb Thin Films for THz Detection
Abstract
:1. Introduction
- the possibility to use Bi-Sb films on dielectric substrates as FSS with satisfactory quality factor;
- the possibility to use Bi-Sb-based FSS for THz detection due to electromagnetic heating;
- the determination the ability of FSS geometry to increase a temperature gradient in the Bi-Sb film.
2. Materials and Methods
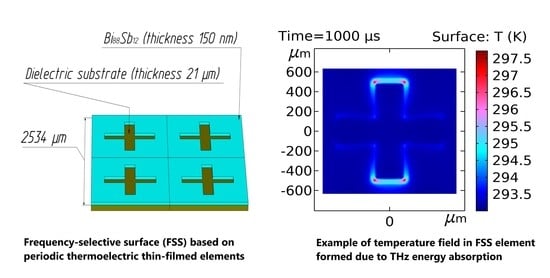
2.1. Geometry of a Frequency-Selective Surface
2.2. Materials
2.3. General Equations
2.4. Boundary Conditions
3. Results
3.1. Filter
3.2. System Heating Due to THz Absorption
3.2.1. Time Step Settings of the Solver
3.2.2. The Impact of Thin Film Description on Temperature Increase Function
3.2.3. The Impact of FSS Geometry and Substrate on Thermal Response
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| THz | terahertz |
| FSS | frequency-selective surface |
| PM | polyimide |
| Q-factor, Q | quality factor |
References
- Mittleman, D.M. Twenty years of terahertz imaging. Opt. Express 2018, 26, 9417–9431. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef] [PubMed]
- Zhong, S. Progress in terahertz nondestructive testing: A review. Front. Mech. Eng. 2019, 14, 273–281. [Google Scholar] [CrossRef]
- Glyavin, M.Y.; Denisov, G.G.; Zapevalov, V.E.; Koshelev, M.A.; Tretyakov, M.Y.; Tsvetkov, A.I. High power terahertz sources for spectroscopy and material diagnostics. Physics-Uspekhi 2016, 59, 595. [Google Scholar] [CrossRef]
- Ren, A.; Zahid, A.; Fan, D.; Yang, X.; Imran, M.A.; Alomainy, A.; Abbasi, Q.H. State-of-the-art in terahertz sensing for food and water security–A comprehensive review. Trends Food Sci. Technol. 2019, 85, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Guerboukha, H.; Nallappan, K.; Skorobogatiy, M. Toward real-time terahertz imaging. Adv. Opt. Photonics 2018, 10, 843–938. [Google Scholar] [CrossRef]
- Tekbıyık, K.; Ekti, A.R.; Kurt, G.K.; Görçin, A. Terahertz band communication systems: Challenges, novelties and standardization efforts. Phys. Commun. 2019, 35, 100700. [Google Scholar] [CrossRef]
- Ghann, W.; Uddin, J. Terahertz (THz) Spectroscopy: A Cutting-Edge Technology; InTech Open: London, UK, 2017. [Google Scholar]
- Lu, X.; Sun, L.; Jiang, P.; Bao, X. Progress of photodetectors based on the photothermoelectric effect. Adv. Mater. 2019, 31, 1902044. [Google Scholar] [CrossRef] [PubMed]
- Gric, T.; Gorodetsky, A.; Trofimov, A.; Rafailov, E. Tunable Plasmonic Properties and Absorption Enhancement in Terahertz Photoconductive Antenna Based on Optimized Plasmonic Nanostructures. J. Infrared. Milli Terahz Waves 2018, 39, 1028–1038. [Google Scholar] [CrossRef]
- Lewis, R.A. A review of terahertz detectors. J. Phys. D Appl. Phys. 2019, 52, 433001. [Google Scholar] [CrossRef]
- Wang, J.; Xie, Z.; Yeow, J.T. Two-dimensional materials applied for room-temperature thermoelectric photodetectors. Mater. Res. Express 2020, 7, 112001. [Google Scholar] [CrossRef]
- Mauser, K.W.; Kim, S.; Mitrovic, S.; Fleischman, D.; Pala, R.; Schwab, K.C.; Atwater, H.A. Resonant thermoelectric nanophotonics. Nat. Nanotechnol. 2017, 12, 770–775. [Google Scholar] [CrossRef]
- Viti, L.; Hu, J.; Coquillat, D.; Politano, A.; Knap, W.; Vitiello, M.S. Efficient Terahertz detection in black-phosphorus nano-transistors with selective and controllable plasma-wave, bolometric and thermoelectric response. Sci. Rep. 2016, 6, 20474. [Google Scholar] [CrossRef] [Green Version]
- Viti, L.; Politano, A.; Zhang, K.; Vitiello, M.S. Thermoelectric terahertz photodetectors based on selenium-doped black phosphorus flakes. Nanoscale 2019, 11, 1995–2002. [Google Scholar] [CrossRef] [Green Version]
- Viti, L.; Cadore, A.R.; Yang, X.; Vorobiev, A.; Muench, J.E.; Watanabe, K.; Taniguchi, T.; Stake, J.; Ferrari, A.C.; Vitiello, M.S. Thermoelectric graphene photodetectors with sub-nanosecond response times at terahertz frequencies. Nanophotonics 2020, 10, 89–98. [Google Scholar] [CrossRef]
- Liu, C.; Du, L.; Tang, W.; Wei, D.; Li, J.; Wang, L.; Chen, G.; Chen, X.; Lu, W. Towards sensitive terahertz detection via thermoelectric manipulation using graphene transistors. NPG Asia Mater. 2018, 10, 318–327. [Google Scholar] [CrossRef] [Green Version]
- Szakmany, G.; Orlov, A.; Bernstein, G.; Porod, W. THz Wave Detection by Antenna-Coupled Nanoscale Thermoelectric Converters. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 582–585. [Google Scholar] [CrossRef]
- Sharma, N.; Bar-David, J.; Mazurski, N.; Levy, U. Metasurfaces for Enhancing Light Absorption in Thermoelectric Photodetectors. ACS Photonics 2020, 7, 2468–2473. [Google Scholar] [CrossRef]
- Su, L.; Yang, S.H.; Huang, I.C.; Tzuang, C.K.C. Design and on-chip measurement of CMOS infrared frequency-selective-surface absorbers for thermoelectric energy harvesting. In Proceedings of the Asia-Pacific Microwave Conference 2011, Melbourne, VIC, Australia, 5–8 December 2011; pp. 461–464. [Google Scholar]
- Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Soleimani, Z.; Zoras, S.; Ceranic, B.; Shahzad, S.; Cui, Y. A review on recent developments of thermoelectric materials for room-temperature applications. Sustain. Energy Technol. Assess. 2020, 37, 100604. [Google Scholar] [CrossRef]
- Alam, H.; Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2013, 2, 190–212. [Google Scholar] [CrossRef]
- Huhn, A.K.; Spickermann, G.; Ihring, A.; Schinkel, U.; Meyer, H.G.; Haring Bolívar, P. Uncooled antenna-coupled terahertz detectors with 22 μs response time based on BiSb/Sb thermocouples. Appl. Phys. Lett. 2013, 102, 121102. [Google Scholar] [CrossRef] [Green Version]
- Zaitsev, A.D.; Demchenko, P.S.; Zykov, D.V.; Korotina, E.A.; Makarova, E.S.; Tkhorzhevskiy, I.L.; Tukmakova, A.S.; Kablukova, N.S.; Asach, A.V.; Novotelnova, A.V.; et al. Optical and Galvanomagnetic Properties of Bi1-xSbx Thin Films in the Terahertz Frequency Range. Appl. Sci. 2020, 10, 2724. [Google Scholar] [CrossRef] [Green Version]
- Khodzitsky, M.K.; Demchenko, P.S.; Zykov, D.V.; Zaitsev, A.D.; Makarova, E.S.; Tukmakova, A.S.; Tkhorzhevskiy, I.L.; Asach, A.V.; Novotelnova, A.V.; Kablukova, N.S. Photothermal, Photoelectric, and Photothermoelectric Effects in Bi-Sb Thin Films in the Terahertz Frequency Range at Room Temperature. Photonics 2021, 8, 76. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, L.; Chen, L.; Bai, J.; Fu, Y. Absorptive frequency selective surface using parallel LC resonance. Electron. Lett. 2016, 52, 418–419. [Google Scholar] [CrossRef]
- Bakshi, S.C.; Mitra, D.; Ghosh, S. A frequency selective surface based reconfigurable rasorber with switchable transmission/reflection band. IEEE Antennas Wirel. Propag. Lett. 2018, 18, 29–33. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, L.; Bai, J.; Fu, Y. Design of absorptive frequency selective surface with good transmission at high frequency. Electron. Lett. 2015, 51, 885–886. [Google Scholar] [CrossRef]
- Ou, H.; Lu, F.; Liao, Y.; Zhu, F.; Lin, Y.S. Tunable terahertz metamaterial for high-efficiency switch application. Results Phys. 2020, 16, 102897. [Google Scholar] [CrossRef]
- Liao, Y.L.; Zhao, Y. Ultra-narrowband dielectric metamaterial absorber with ultra-sparse nanowire grids for sensing applications. Sci. Rep. 2020, 10, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shahounvand, H.; Fard, A. Design and simulation of a new narrow terahertz bandpass filter. SN Appl. Sci. 2020, 2, 1–7. [Google Scholar] [CrossRef]
- Kim, S.M.; Leite, C.M.; Park, J.Y.; Kim, H.J.; Jang, J.H. Multiband Terahertz Self-Complementary Metasurface. IEEE Access 2020, 8, 199051–199059. [Google Scholar] [CrossRef]
- Anwar, R.S.; Mao, L.; Ning, H. Frequency selective surfaces: A review. Appl. Sci. 2018, 8, 1689. [Google Scholar] [CrossRef] [Green Version]
- Guan, F.; Xiao, H.; Shi, M.; Wang, F. The novel frequency selective fabric and application research. J. Ind. Text. 2016, 46, 143–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Miao, L.; Guo, S.; Huang, Z.; Cao, Z.; He, Y.; Wei, J.; Li, C.; Jiang, J. A broadband tunable frequency selective surface absorber for oblique incidence applications. J. Phys. D Appl. Phys. 2019, 53, 055105. [Google Scholar] [CrossRef]
- Liu, N.; Sheng, X.; Zhang, C.; Guo, D. Design of frequency selective surface structure with high angular stability for radome application. IEEE Antennas Wirel. Propag. Lett. 2017, 17, 138–141. [Google Scholar] [CrossRef]
- Chatterjee, A.; Parui, S.K. Frequency-dependent directive radiation of monopole-dielectric resonator antenna using a conformal frequency selective surface. IEEE Trans. Antennas Propag. 2017, 65, 2233–2239. [Google Scholar] [CrossRef]
- Li, D.; Li, T.W.; Li, E.P.; Zhang, Y.J. A 2.5-D angularly stable frequency selective surface using via-based structure for 5G EMI shielding. IEEE Trans. Electromagn. Compat. 2017, 60, 768–775. [Google Scholar] [CrossRef]
- Chen, H.T.; Padilla, W.J.; Averitt, R.D.; Gossard, A.C.; Highstrete, C.; Lee, M.; O’Hara, J.F.; Taylor, A.J. Electromagnetic metamaterials for terahertz applications. Terahertz Sci. Technol. 2008, 1, 42–50. [Google Scholar]
- Dong, B.; Ma, H.; Wang, J.; Shi, P.; Li, J.; Zhu, L.; Lou, J.; Feng, M.; Qu, S. A thermally tunable THz metamaterial frequency-selective surface based on barium strontium titanate thin film. J. Phys. D Appl. Phys. 2018, 045301, 045301. [Google Scholar] [CrossRef]
- Porterfield, D.W.; Hesler, J.; Densing, R.; Mueller, E.; Crowe, T.; Weikle, R. Resonant metal-mesh bandpass filters for the far infrared. Appl. Opt. 1994, 33, 6046–6052. [Google Scholar] [CrossRef]
- Makarova, E.; Tukmakova, A.; Novotelnova, A.; Kablukova, N. Nanoscale films of bismuth and antimony: Production technologies and properties. J. Phys. Conf. Ser. 2019, 1400, 055048. [Google Scholar] [CrossRef]
- Terasense. Available online: https://terasense.com/ (accessed on 6 March 2021).
- Naftaly, M. Terahertz Metrology; Artech House: London, UK, 2015. [Google Scholar]
- Tinkham, M. Energy gap interpretation of experiments on infrared transmission through superconducting films. Phys. Rev. 1956, 104, 845. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Tukmakova, A.S.; Asach, A.V.; Novotelnova, A.V.; Tkhorzhevskiy, I.L.; Kablukova, N.S.; Demchenko, P.S.; Zaitsev, A.D.; Khodzitsky, M.K. FEM Simulation of THz Detector Based on Sb and Bi88Sb12 Thermoelectric Thin Films. Appl. Sci. 2020, 10, 1929. [Google Scholar] [CrossRef] [Green Version]
- Gockenbach, M.; Schmidtke, K. Newton’s law of heating and the heat equation. Involv. A J. Math. 2009, 2, 419–437. [Google Scholar] [CrossRef] [Green Version]









| Frequency, THz | Bi88Sb12 (On Mica) | Bi88Sb12 (on PM) | Mica | Polyimide |
|---|---|---|---|---|
| 0.1 | −20,000 | −18,000 | 5.2 | 2.5 |
| 0.14 | −22,000 | −16,000 | 5.2 | 2.5 |
| Frequency, THz | Bi88Sb12 (On Mica) | Bi88Sb12 (on PM) | Mica | Polyimide |
|---|---|---|---|---|
| 0.1 | 127,000 | 45,000 | 0.2 | 0.9 |
| 0.14 | 104,000 | 38,000 | 0.2 | 0.9 |
| Frequency, THz | Bi88Sb12 (On Mica) | Bi88Sb12 (on PM) | Mica | Polyimide |
|---|---|---|---|---|
| 0.1 | 934,000 | 313,000 | ||
| 0.14 | 866,000 | 320,000 |
| Component | Bi88Sb12 | Mica | Polyimide |
|---|---|---|---|
| cross-plane | 4 | 0.5 | 0.3 |
| in-plane | 8 | 5 | 0.3 |
| Frequency, THz | Substrate | P, μm | L, μm | W, μm |
|---|---|---|---|---|
| 0.1 | mica | 1511 | 1358 | 380 |
| 0.1 | PM | 1511 | 1380 | 380 |
| 0.14 | mica | 1267 | 950 | 285 |
| 0.14 | PM | 1267 | 990 | 285 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tukmakova, A.; Tkhorzhevskiy, I.; Sedinin, A.; Asach, A.; Novotelnova, A.; Kablukova, N.; Demchenko, P.; Zaitsev, A.; Zykov, D.; Khodzitsky, M. FEM Simulation of Frequency-Selective Surface Based on Thermoelectric Bi-Sb Thin Films for THz Detection. Photonics 2021, 8, 119. https://doi.org/10.3390/photonics8040119
Tukmakova A, Tkhorzhevskiy I, Sedinin A, Asach A, Novotelnova A, Kablukova N, Demchenko P, Zaitsev A, Zykov D, Khodzitsky M. FEM Simulation of Frequency-Selective Surface Based on Thermoelectric Bi-Sb Thin Films for THz Detection. Photonics. 2021; 8(4):119. https://doi.org/10.3390/photonics8040119
Chicago/Turabian StyleTukmakova, Anastasiia, Ivan Tkhorzhevskiy, Artyom Sedinin, Aleksei Asach, Anna Novotelnova, Natallya Kablukova, Petr Demchenko, Anton Zaitsev, Dmitry Zykov, and Mikhail Khodzitsky. 2021. "FEM Simulation of Frequency-Selective Surface Based on Thermoelectric Bi-Sb Thin Films for THz Detection" Photonics 8, no. 4: 119. https://doi.org/10.3390/photonics8040119
APA StyleTukmakova, A., Tkhorzhevskiy, I., Sedinin, A., Asach, A., Novotelnova, A., Kablukova, N., Demchenko, P., Zaitsev, A., Zykov, D., & Khodzitsky, M. (2021). FEM Simulation of Frequency-Selective Surface Based on Thermoelectric Bi-Sb Thin Films for THz Detection. Photonics, 8(4), 119. https://doi.org/10.3390/photonics8040119