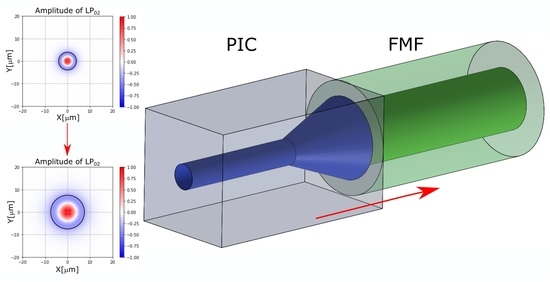
Interconnection of Few-Mode Fibers and Photonic Integrated Circuits Using Mode-Field Adapters
Abstract
:1. Introduction
2. Methods
3. Results
3.1. Modal Distribution in MFAs
3.2. Coupling Efficiency and Losses
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minzioni, P.; Lacava, C.; Tanabe, T.; Dong, J.; Hu, X.; Csaba, G.; Porod, W.; Singh, G.; Willner, A.E.; Almaiman, A.; et al. Roadmap on all-optical processing. J. Opt. 2019, 21, 063001. [Google Scholar] [CrossRef]
- Shi, W.; Tian, Y.; Gervais, A. Scaling capacity of fiber-optic transmission systems via silicon photonics. Nanophotonics 2020, 9, 4629–4663. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef] [Green Version]
- Sinatkas, G.; Christopoulos, T.; Tsilipakos, O.; Kriezis, E.E. Electro-optic modulation in integrated photonics. J. Appl. Phys. 2021, 130, 010901. [Google Scholar] [CrossRef]
- Huang, L.; Xu, L.; Woolley, M.; Miroshnichenko, A.E. Trends in quantum nanophotonics. Adv. Quantum Technol. 2020, 3, 1900126. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Leon-Saval, S.G.; Fontaine, N.K.; Salazar-Gil, J.R.; Ercan, B.; Ryf, R.; Bland-Hawthorn, J. Mode-selective photonic lanterns for space-division multiplexing. Opt. Express 2014, 22, 1036–1044. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Rademacher, G.; Luís, R.S. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
- Son, G.; Han, S.; Park, J.; Kwon, K.; Yu, K. High-efficiency broadband light coupling between optical fibers and photonic integrated circuits. Nanophotonics 2018, 7, 1845–1864. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Hu, T.; Dong, B.; Luo, X.; Liow, T.Y.; Song, J.; Lee, C.; Lo, G.Q. Silicon photonic platforms for mid-infrared applications. Photonics Res. 2017, 5, 417–430. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Luo, Z.; Gu, T.; Kimerling, L.C.; Wada, K.; Agarwal, A.; Hu, J. Mid-infrared integrated photonics on silicon: A perspective. Nanophotonics 2018, 7, 393–420. [Google Scholar] [CrossRef]
- Han, X.Y.; Wu, Z.L.; Yang, S.C.; Shen, F.F.; Liang, Y.X.; Wang, L.H.; Wang, J.Y.; Ren, J.; Jia, L.Y.; Zhang, H.; et al. Recent progress of imprinted polymer photonic waveguide devices and applications. Polymers 2018, 10, 603. [Google Scholar] [CrossRef] [Green Version]
- Maram, R.; Kaushal, S.; Azaña, J.; Chen, L.R. Recent trends and advances of silicon-based integrated microwave photonics. Photonics 2019, 6, 13. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, P.I.; Blaicher, M.; Reuter, I.; Billah, M.; Hoose, T.; Hofmann, A.; Caer, C.; Dangel, R.; Offrein, B.; Troppenz, U.; et al. In situ 3D nanoprinting of free-form coupling elements for hybrid photonic integration. Nat. Photonics 2018, 12, 241–247. [Google Scholar] [CrossRef]
- Kohli, N.; Ménard, M.; Winnie, N.Y. Efficient TE/TM spot-size converter for broadband coupling to single mode fibers. OSA Contin. 2019, 2, 2428–2438. [Google Scholar] [CrossRef]
- Vanmol, K.; Baghdasaryan, T.; Vermeulen, N.; Saurav, K.; Watté, J.; Thienpont, H.; Van Erps, J. 3D direct laser writing of microstructured optical fiber tapers on single-mode fibers for mode-field conversion. Opt. Express 2020, 28, 36147–36158. [Google Scholar] [CrossRef]
- Gordillo, O.A.J.; Dave, U.D.; Lipson, M. One-to-one coupling higher order modes in a fiber to higher order modes in silicon waveguide. In Proceedings of the 2021 Conference on Lasers and Electro-Optics (CLEO), Virtual Event. 20–24 June 2021; pp. 1–2. [Google Scholar]
- Cheng, L.; Mao, S.; Chen, Z.; Wang, Y.; Zhao, C.; Fu, H. Ultra-compact dual-mode mode-size converter for silicon photonic few-mode fiber interfaces. Opt. Express 2021, 29, 33728–33740. [Google Scholar] [CrossRef]
- Sillard, P.; Bigot-Astruc, M.; Molin, D. Few-mode fibers for mode-division-multiplexed systems. J. Light. Technol. 2014, 32, 2824–2829. [Google Scholar] [CrossRef]
- Kumar, A.; Nambiar, S.; Kallega, R.; Ranganath, P.; Ea, P.; Selvaraja, S.K. High-efficiency vertical fibre-to-polymer waveguide coupling scheme for scalable polymer photonic circuits. Opt. Express 2021, 29, 9699–9710. [Google Scholar] [CrossRef]
- Park, S.R.; O, B.H. Novel design concept of waveguide mode adapter for low-loss mode conversion. IEEE Photonics Technol. Lett. 2001, 13, 675–677. [Google Scholar] [CrossRef]
- Mu, X.; Wu, S.; Cheng, L.; Fu, H. Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 2020, 10, 1538. [Google Scholar] [CrossRef] [Green Version]
- Hardy, I.; Grosso, P.; Bosc, D. Design and fabrication of mode size adapter in a photosensitive polymer waveguide. IEEE Photonics Technol. Lett. 2005, 17, 1028–1030. [Google Scholar] [CrossRef]
- Qi, W.; Yu, Y.; Zhang, X. On-chip arbitrary-mode spot size conversion. Nanophotonics 2020, 9, 4365–4372. [Google Scholar] [CrossRef]
- Baldacchini, T. Three-Dimensional Microfabrication Using Two-Photon Polymerization: Fundamentals, Technology, and Applications; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]
- Choudhury, D.; Macdonald, J.R.; Kar, A.K. Ultrafast laser inscription: Perspectives on future integrated applications. Laser Photonics Rev. 2014, 8, 827–846. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; de Aldana, J.V. Optical waveguides in crystalline dielectric materials produced by femtosecond-laser micromachining. Laser Photonics Rev. 2014, 8, 251–275. [Google Scholar] [CrossRef]
- Wu, Z.L.; Qi, Y.N.; Yin, X.J.; Yang, X.; Chen, C.M.; Yu, J.Y.; Yu, J.C.; Lin, Y.M.; Hui, F.; Liu, P.L.; et al. Polymer-based device fabrication and applications using direct laser writing technology. Polymers 2019, 11, 553. [Google Scholar] [CrossRef] [Green Version]
- Do, M.T.; Nguyen, T.T.N.; Li, Q.; Benisty, H.; Ledoux-Rak, I.; Lai, N.D. Submicrometer 3D structures fabrication enabled by one-photon absorption direct laser writing. Opt. Express 2013, 21, 20964–20973. [Google Scholar] [CrossRef]
- Lindenmann, N.; Balthasar, G.; Hillerkuss, D.; Schmogrow, R.; Jordan, M.; Leuthold, J.; Freude, W.; Koos, C. Photonic wire bonding: A novel concept for chip-scale interconnects. Opt. Express 2012, 20, 17667–17677. [Google Scholar] [CrossRef] [Green Version]
- Matsui, T.; Nakajima, K.; Sakamoto, T. Effective mode-field diameter for few-mode fibers for considering splice loss characteristics. Appl. Opt. 2017, 56, 7484–7490. [Google Scholar] [CrossRef]
- Nakamura, A.; Iida, D. Mode field diameter definitions for few-mode fibers based on spot size of higher-order Gaussian mode. IEEE Photonics J. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Nakamura, A.; Okamoto, K.; Koshikiya, Y.; Manabe, T. Effective mode field diameter for LP 11 mode and its measurement technique. IEEE Photonics Technol. Lett. 2016, 28, 2553–2556. [Google Scholar] [CrossRef]
- Love, J.; Henry, W.; Stewart, W.; Black, R.; Lacroix, S.; Gonthier, F. Tapered single-mode fibres and devices. Part 1: Adiabaticity criteria. IEE Proc. J. (Optoelectron.) 1991, 138, 343–354. [Google Scholar] [CrossRef]
- Black, R.; Lacroix, S.; Gonthier, F.; Love, J. Tapered single-mode fibres and devices. II. Experimental and theoretical quantification. IEE Proc. J. (Optoelectron.) 1991, 138, 355–364. [Google Scholar] [CrossRef]
- Sun, X.; Liu, H.C.; Yariv, A. Adiabaticity criterion and the shortest adiabatic mode transformer in a coupled-waveguide system. Opt. Lett. 2009, 34, 280–282. [Google Scholar] [CrossRef] [Green Version]
- Zou, J.; Yu, Y.; Ye, M.; Liu, L.; Deng, S.; Xu, X.; Zhang, X. Short and efficient mode-size converter designed by segmented-stepwise method. Opt. Lett. 2014, 39, 6273–6276. [Google Scholar] [CrossRef]
- Martínez-Garaot, S.; Ruschhaupt, A.; Gillet, J.; Busch, T.; Muga, J.G. Fast quasiadiabatic dynamics. Phys. Rev. A 2015, 92, 043406. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Garaot, S.; Muga, J.G.; Tseng, S.Y. Shortcuts to adiabaticity in optical waveguides using fast quasiadiabatic dynamics. Opt. Express 2017, 25, 159–167. [Google Scholar] [CrossRef] [Green Version]
- Liang, T.L.; Tu, Y.; Chen, X.; Huang, Y.; Bai, Q.; Zhao, Y.; Zhang, J.; Yuan, Y.; Li, J.; Yi, F.; et al. A Fully Numerical Method for Designing Efficient Adiabatic Mode Evolution Structures (Adiabatic Taper, Coupler, Splitter, Mode Converter) Applicable to Complex Geometries. J. Light. Technol. 2021, 39, 5531–5547. [Google Scholar] [CrossRef]
- Sullivan, A.C.; Grabowski, M.W.; McLeod, R.R. Three-dimensional direct-write lithography into photopolymer. Appl. Opt. 2007, 46, 295–301. [Google Scholar] [CrossRef]
- Kayaku Advanced Materials. Permanent Negative Epoxy Photoresist Technical Data Sheet; Kayaku Advanced Materials: Westborough, MA, USA, 2020; Version 1. [Google Scholar]
- Glugla, D.J.; Chosy, M.B.; Alim, M.D.; Childress, K.K.; Sullivan, A.C.; McLeod, R.R. Multiple patterning of holographic photopolymers for increased refractive index contrast. Opt. Lett. 2018, 43, 1866–1869. [Google Scholar] [CrossRef] [PubMed]
- Sillard, P.; Bigot-Astruc, M.; Boivin, D.; Maerten, H.; Provost, L. Few-mode fiber for uncoupled mode-division multiplexing transmissions. In Proceedings of the 2011 37th European Conference and Exhibition on Optical Communication, Geneva, Switzerland, 18–22 September 2011; pp. 1–3. [Google Scholar]
- Siriani, D.F.; Tambasco, J.L. Adiabatic guided wave optics—A toolbox of generalized design and optimization methods. Opt. Express 2021, 29, 3243–3257. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.L.; Liang, F.C.; Chung, H.C.; Tseng, S.Y. Adiabaticity engineering in optical waveguides. Opt. Express 2020, 28, 30117–30129. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Zhang, R. Metamaterial-based ultrashort multimode waveguide taper with low intermodal crosstalk. Opt. Express 2021, 29, 7124–7133. [Google Scholar] [CrossRef]








| Absolute Difference [ ] | ||||
|---|---|---|---|---|
| Profile | ||||
| E1 | 1.16954 | 4.5423 | 16.47 | 27.6501 |
| E2 | 6.68414 | 0.4097 | 11.4588 | 23.3423 |
| E3 | 20.19844 | 12.599 | 0.8102 | 13.1484 |
| E4 | 40.01824 | 30.377 | 18.7898 | 1.8302 |
| Linear/Exp | 21.52505 | 24.35765 | 36.4133 | 44.18398 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Cortez, O.; Velázquez-Benítez, A.M. Interconnection of Few-Mode Fibers and Photonic Integrated Circuits Using Mode-Field Adapters. Photonics 2022, 9, 319. https://doi.org/10.3390/photonics9050319
González-Cortez O, Velázquez-Benítez AM. Interconnection of Few-Mode Fibers and Photonic Integrated Circuits Using Mode-Field Adapters. Photonics. 2022; 9(5):319. https://doi.org/10.3390/photonics9050319
Chicago/Turabian StyleGonzález-Cortez, Oscar, and Amado M. Velázquez-Benítez. 2022. "Interconnection of Few-Mode Fibers and Photonic Integrated Circuits Using Mode-Field Adapters" Photonics 9, no. 5: 319. https://doi.org/10.3390/photonics9050319
APA StyleGonzález-Cortez, O., & Velázquez-Benítez, A. M. (2022). Interconnection of Few-Mode Fibers and Photonic Integrated Circuits Using Mode-Field Adapters. Photonics, 9(5), 319. https://doi.org/10.3390/photonics9050319