Next Article in Journal
Synthesis, Photophysical Properties, and Toxicity of o-Xylene-Bridged Porphyrin Dimers
Next Article in Special Issue
Combined Effect of Halogenation and SiO2 Addition on the Li-Ion Conductivity of LiBH4
Previous Article in Journal
Hydrazine Oxidation in Aqueous Solutions I: N4H6 Decomposition
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 11
Issue 10
10.3390/inorganics11100414
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Heavy-Fermion Properties of Yb2Pd2SnH≈2

by
Silvie Maskova-Cerna
1,
Ernst Bauer
2,
Mauro Giovannini
3 and
Ladislav Havela
1,*
1
Department of Condensed Matter Physics, Charles University, CZ-12116 Prague, Czech Republic
2
Institute of Solid State Physics, Vienna University of Technology, A-1040 Wien, Austria
3
Dipartimento di Chimica e Chimica Industriale, University of Genova, I-16146 Genova, Italy
*
Author to whom correspondence should be addressed.
Inorganics 2023, 11(10), 414; https://doi.org/10.3390/inorganics11100414
Submission received: 18 September 2023 / Revised: 4 October 2023 / Accepted: 14 October 2023 / Published: 18 October 2023
(This article belongs to the Special Issue A Themed Issue in Honor of Prof. Radovan Cerny—Materials Science, Energy Storage, Diffraction and Crystal Chemistry)
Browse Figures
Versions Notes

Abstract

:
A hydride of Yb2Pd2Sn could be synthesized with approximately 2 H atoms per f.u. The hydrogenation leads to a volume expansion while preserving the tetragonal symmetry (P4/mbm). The lattice reaction is strongly anisotropic, and the 5% expansion in c is partly compensated by the 0.5% compression in a. The hydride is paramagnetic at least down to 0.5 K. Yb remains at or very close to the 3+ (4f13) state, as in Yb2Pd2Sn. Specific heat C/T vs. T shows an upturn existing already in Yb2Pd2Sn, but it is much more pronounced in the hydride (1.8 J/mol f.u. K2 for T → 0, i.e., more than twice higher than in its precursor). This is interpreted as lowering the Kondo temperature due to H bonding.

Graphical Abstract

1. Introduction

The R2T2X (R = rare-earth, T = transition metal, X = p-metal) series represents an extended group of materials, recently attracting lot of attention [1,2,3,4,5,6,7,8]. Although several different crystal structures have been identified for the given stoichiometry [9], most research effort has been focused on the family of tetragonal compounds with the Mo2FeB2 structure (ordered ternary derivative of the U3Si2 type). The fact that they include both rare-earths and actinides (standing for the element R) allows a direct comparison of the 4f and 5f magnetism. The specific coordination of the R element in the crystal lattice (Figure 1b), forming dimers arranged in a square motif in the basal plane, can in certain situations provide realization of the frustrated lattice of the Shastry–Sutherland type (Figure 1) [10]. Magnetic frustration exists when the near-neighbor (NN) interactions J′ and next-nearest-neighbor (NNN) J are antiferromagnetic (see Figure 1a). Depending on the ratio of the intradimer and interdimer exchange parameters, J′, J, different ground states occur [11,12,13].
There are two limiting behaviors, depending on J/J′. Nonordering dimers are found for small J/J′, distinguished by an energy gap Δ between the singlet and triplet states of the dimer (disordered ‘spin liquid’ (SL) regime). On the other hand, AF order with gapless magnetic excitations is favored for large J/J′. At T = 0, a transition between the SL and AF phases has been predicted for J/J′ ≈ 0.6–0.7 [14]. Some “221” compounds were already identified as compounds with Shastry–Sutherland lattice [13,14,15,16].
Tuning, e.g., by composition modifications, gives access to a quantum critical point, where the long-range magnetic order vanishes [17,18]. The behavior of metallic systems around such singularities has been a driving force behind the research of strongly correlated systems. Last, but not least, the capability to absorb hydrogen provides the possibility to tune electronic properties by a lattice expansion and by bonding of H atoms in one or more interstitial positions. Moreover, changes of symmetry sometimes occur, too, affecting physical properties ([19] and references within).
In general, anomalous rare-earths with unstable 4f configuration deserve special attention among all rare-earth compounds. The 4f instability has been traditionally encountered at Ce, Sm, Eu, or Yb compounds, for which composition or external variables can be used to tune a system between a magnetic and nonmagnetic state. While Ce systems offer a possibility to suppress a magnetic state by applied pressure, driving the system via Kondo regime to intermediate-valence state reducing the 4f occupancy below 1, Yb behaves, to some extent, in an opposite way, with high pressure naturally preferring a low-volume state, i.e., the magnetic 4f13 one. Valence fluctuations between f13 and nonmagnetic f14 are therefore suppressed by the lattice compression. However, the 4f13 magnetism has to be ultimately attenuated if even higher pressures are applied, which was indeed demonstrated for Yb2Pd2Sn [20]. A particularly interesting fact is that this compound as well as its counterpart Yb2Pd2In are nonmagnetic at ambient pressures [21], but a small unit-cell contraction roughly in the middle of the quasi-ternary system is sufficient to induce magnetic order [21] in a similar way as a pressure around 1 GPa in pure Yb2Pd2Sn [20].
Hydrogen absorption without a dramatic change of crystal-structure type can be taken to some extent as a stimulus acting opposite to hydrostatic pressure. The system reacts on a H absorption by a volume expansion due to H atoms occupying particular interstitial positions. In actinides, sensitive to distances between neighbor 5f atoms, this tunes the width of the 5f band responsible for magnetism, supporting the tendency to formation of moments and their ordering [18]. The response in rare-earths is more complex. One can try to separate the impact on the stability of ionic magnetic moments from variations of intersite exchange interactions. The latter aspect is dominant in systems with regular rare-earths, affected mainly by the loss of conduction-electron concentration, weakening the indirect RKKY exchange interactions. This interaction has certain dependence on interatomic spacing d (the RKKY interaction [22] has oscillatory sign and its envelope decays as 1/d3), but the density of conduction electrons plays a major role. In an ultimate case of loss of metallicity, the RKKY interaction vanishes. Ordering temperatures are consequently reduced, e.g., TC in GdH3 is lower by two orders of magnitude than in Gd metal (TC = 297 K). The reason is that H in the hydrides behaves as an acceptor of electrons in the presence of strongly electropositive lanthanides. For example, transfer of 0.34 e− towards the H-1s states was observed in GdH3 [23,24]. This phenomenon is another manifestation of the switchable mirror effect [25], based on the reversible loss of metallicity between YH2 and YH3. Naturally no visible magnetic response is recorded for Y without f-electrons. The weakening of intersite exchange interactions can be seen even in other R-based compounds having more elements, although the effect may be suppressed due to valence-band electrons brought into the system by other constituents. Examples of RTX (e.g., RNiAl or R2T2X compounds exhibit reduction in respective ordering temperatures typically by an order of magnitude upon hydrogenation (R = rare-earth)). In compounds with electropositive elements, Ni carries no magnetic moments, having the 3d band effectively filled up [26]. This implies that the reduction is due to the impact of H on the RKKY interaction. For example, in the ferromagnetic compound GdNiAl, TN = 62 K decreases to 15 K in the saturated hydride GdNiAlH1.35 [27]. The influence of hydrogenation on the ordering temperatures approximately following the De Gennes scaling [28] is analogical for other R. However, in compounds like GdTiGe (ferromagnet with TC = 376 K), where Gd form tetrahedra, which are all occupied by H in the hydride, the effect is similarly striking as in pure Gd, reducing TC from 376 K to less than 4 K [29].
A similar development of the density of states can be observed in R2T2X compounds, and the suppression of ordering temperatures is found. For example, Nd2Ni2Mg is antiferromagnetic with TN = 19 K, whereas TN = 1.0 K in Nd2Ni2MgH8 [19]. Lower H concentrations make naturally the drop less striking; TN = 12 K in Tb2Pd2InH1.6 should be compared with TN = 33 K in Tb2Pd2In [30].
A particular interest is in rare-earths with unstable 4f configuration (anomalous rare-earths), with stronger 4f hybridization with conduction-electron states. In Ce compounds, any volume expansion prefers the 4f1 stability, and suppression of valence fluctuations leading to a Kondo state or even to magnetic ordering of stable 4f moments. The same tendency is supported by reducing the density of non-f states at the Fermi level by the H bonding, but, due to the same reason, the intersite coupling (RKKY like) also remains weak. The development of ordering temperatures is therefore nonmonotonous, as proposed in the general Doniach phase diagram, illustrating evolution from weakly paramagnetic valence fluctuators through Kondo or Kondo lattice systems into magnetically ordered systems. The highest (but still rather low) ordering temperatures appear close to the very onset of magnetic order. Such tendency was found for CeRuSi [31], where antiferromagnetism (TN = 7.5 K) is induced by hydrogen from the nonmagnetic heavy Fermion precursor compound. In Ce2Ni2InHx there occurs a change from valence fluctuations in the parent compound to rather stable 4f1 configuration in the hydride with x = 4.98 [32]. The hydrogenation works, hence, opposite to the common effect of high pressure, a usual tuning mechanism. Unlike pressure tuning, the hydrogenation does not yield a continuous scale, but it is the only “negative pressure” tool available.
Exceptionally, the opposite influence of H, where the magnetism is not supported by H absorption, was observed. CeCoSi, which is antiferromagnetic (TN = 8.8 K), has the magnetic order destabilized in CeCoSiH (CeCoSiH is an intermediate valence compound) [33]. In such a case, the H bonding can arguably affect the 4f states, providing a plausible explanation. In general, the situation in which the increasing H concentration leads to a slow decrease in ordering temperatures is more common.
With regard to the R2T2X compounds, such development was described for Ce2Pd2In, which allows the tuning of the H concentration in several steps up to 4 H/f.u. [34] or Ce2Cu2In [35]. A general conclusion from the available data is that particular details of the development of magnetism upon H exposure can be then an interesting probe into a system, revealing important details of electronic structure. Yb compounds with hydrogen have been studied much less, hence the tunability still remains to be explored. The 4f14 configuration of free Yb ion is preserved in YbH2 in contrast with intermediate valence state for higher H concentrations [36]. YbH2 is nonmetallic and naturally nonmagnetic. It does not adopt the cubic CaF2 structure characteristic for other rare-earth dihydrides, but crystallizes in an orthorhombic structure known for CaH2 [37]. This is related to the fact that divalent rare-earths do not have the bonding properties of a d-electron. The 4f13 state appears only in YbH3, which orders antiferromagnetically below TN ≈ 4 K [38]. The case of Yb2Pd2Sn-H is of a special interest as the precursor of the hydride is close to the onset of magnetism.
In the present paper, we describe crystal structure and basic properties of its hydride, being isostructural with other members of the extended R2Pd2Sn-H family.

2. Results

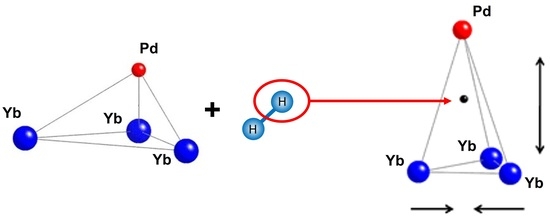
2.1. Crystal Structure

There is extended information on systematic variations of crystal structure of R2Pd2(In,Sn) compounds affected by hydrogen [30]. This study, however, did not include compounds with Yb. It was found that the lattice parameters a and c decrease linearly with increasing atomic number both in parent compounds as well as in their hydrides. The lattice parameter a for the hydrides is also linearly decreasing with increasing atomic number as in the parent compounds, but the slope is much higher. For first part of the R series (La–Gd), the hydrogen absorption leads to expansion along the a-axis, while for the others, the a parameter contracts. On the other hand, the lattice is expanding along the c-axis in all studied R2Pd2(In,Sn) compounds. The relative expansion along the c-direction, ∆c/c, increases with increasing atomic number of R in such a way that it compensates for the lattice contraction along the a-axis, leading to volume expansion in all cases, although it decreases from 6% to 3.5% with increasing atomic number Z.
The crystal structure of a polycrystalline Yb2Pd2Sn sample was proved to be of the correct tetragonal Mo2FeB2 type (space group P4/mbm). The hydrogenation leads to a volume expansion while preserving the tetragonal symmetry, which is known from other R2T2X compounds as the first hydrogenation step [30]. Table 1 shows that the structure response (Δa/a and Δc/c) is anisotropic, with expansion of the unit cell along the c-axis and compression along a. The respective diffraction patterns are shown in Figure 2. The lattice parameters and other details are given in Table 1. For the hydride, one can distinguish one peak of the spurious YbPd2Sn phase [39,40] around 2θ ≈ 38°. The same amount (around 1.6%) was present in the precursor alloy; hence, we conclude that this phase is not affected by hydrogenation.
The amount of hydrogen absorbed was determined to be (1.8 ± 0.2) H at./f.u., analogous to other R2T2X hydrides that preserve the tetragonal symmetry [30]. This implies that H atoms occupy half of the adjacent Yb3Pd tetrahedra. Occupancy of all tetrahedra would violate the rule that two tetrahedra sharing the same face cannot be occupied simultaneously [41]. Similar values of internal parameters characterizing the Yb positions in Yb2Pd2Sn and its hydride indicate that the basal-plane square motif of Yb atoms reacts to hydrogenation by practically isotropic expansion. The absence of significant rotation of the square, permitted otherwise within the given tetragonal symmetry (and attested in some R2T2X compounds, e.g., as due to thermal expansion or external pressure [42]), suggests the absence of any dramatic impact of hydrogenation on the effective size of Yb atoms. We can assume that if the Yb size varied it would mainly impact the Yb–Yb distance within each dimer, which gives a rotation of the Yb square motif within the basal plane.
The lattice parameters, and particularly the negative value of Δa/a, clearly indicate that Yb stays rather close to the 3+ state in the hydride. Figure 3 shows that the 2+ state with much larger volume would place the relative change entirely out of systematics. Despite the volume change, the shortest Yb–Yb distance remains practically the same (below 0.4%) (Table 1). It is only switched from the c-axis in the parent compound to the basal plane in the hydride.

2.2. Magnetic Properties

Temperature dependence of magnetic susceptibility (Figure 4) reveals only modest differences between Yb2Pd2Sn and its hydride. In both cases, we observed a monotonous increase in χ(T) with decreasing T (Figure 4a), with no sign of a magnetic phase transition in the temperature range studied, i.e., above T = 2 K. The inverse susceptibility 1/χ(T) in the field of 1 T seen in Figure 4b can be approximated by a straight line, indicating the Curie–Weiss behavior χ = C/(T − θp), from which the value of C gives the effective magnetic moment value μeff. The fits (30–300 K) yield μeff = 3.64 μB/Yb, θP = −27 K for Yb2Pd2Sn and μeff = 3.28 μB/Yb, θP = −13 K for Yb2Pd2SnH≈2. The fact that μeff does not reach the full theoretical value for 4f13 (4.54 µB) could be related to a small admixture of the 4f14 state with µeff = 0. However, as shown above, no significant 4f14 participation is expected on the basis of structure considerations. Alternatively, the reduced µeff in the hydride may be related to a structural disorder due to incomplete occupation of the H sublattice, which could locally change the exchange interactions and introduce magnetic frustration, leading to a distribution of θP values. That also affects the µeff values obtained from the fit and can be a reason for the small but visible bending of the 1/χ(T) dependence seen in Figure 4. More generally, the reduction in µeff can be related to the crystal electric field effect. The negative values of θP can be due to dominant intersite antiferromagnetic coupling as well as the Kondo effect [43], i.e., the moment instability due to the 4f hybridization with ligand electronic states, which can be expected to be close to the 4f13 state of Yb.
The 4f occupation enhanced over n = 13 is unlikely also from the point of view of H bonding, in which the H atom plays a role of acceptor in compounds with more electropositive element. In addition, any considerable 4f14 mixing would give more valence fluctuations and suppression of the Kondo effect. Hence the γ-enhancement (see below) would be difficult to understand.
Figure 4b reveals how the deviation of magnetic susceptibility of Yb2Pd2SnH≈2 from the Curie–Weiss behavior develops progressively below ≈ 40 K. This effect is actually strongly field-dependent, as seen in Figure 5. The prominent upturn seen in low fields becomes gradually suppressed with increasing field. Figure 6 demonstrates that in the highest field applied we can see a certain tendency to saturation of magnetization to values 2.5–3.0 µB/f.u., which is still far below the value expected for full theoretical moment (8.0 µB/f.u., i.e., 4.0 µB/Yb). χ(T) increasing with decreasing T faster than the Curie–Weiss law extrapolated from high temperatures can be, in a most simple model, attributed to a small amount of Yb moments, which do not experience (e.g., due to the atomic disorder in the hydride) the negative exchange coupling to the neighbors. In such a situation, the Curie behavior (θp = 0) starts to dominate χ(T) as T → 0 and such moments are actually easier oriented by the magnetic field.
The field dependence of χ(T) has to be naturally projected into a nonlinearity of field dependence of magnetization, which exhibits a saturating tendency. Qualitatively, it can be attributed to the saturation of the Brillouin function. As the paramagnetic Curie temperature θp = −13 K, the measured magnetization at T = 2 K can be compared in the first approximation with a simulated case of noninteracting moments at T = 15 K. Figure 6 shows that the agreement is unsatisfactory. The magnetization tends to saturate in much smaller fields and the shape resembles more the Brillouin function at T = 2 K, but the total magnetization values from the experiment are, by far, too low, reaching only 2.5 µB/f.u., which should be compared with the full theoretical moment 8.0 µB/f.u. considering 2 Yb atoms in f.u. Only a small part of the discrepancy can be related to magnetic anisotropy of the polycrystalline sample. In the most extreme case of uniaxial anisotropy, random orientation of grains can reduce macroscopic magnetization by 50%. Here, the effect is clearly higher so we cannot exclude the presence of, e.g., antiferromagnetic coupling of the dimers existing in the paramagnetic state, which would imply a metamagnetic process in magnetic fields beyond our experimental limit of 14 T.

2.3. Specific Heat

The results of the specific heat measurement (seen in Figure 7 in the C/T vs. T representation) show a gradual approach to the classical limit of lattice heat capacity, 15*R = 124.72 J/mol K for the formula unit containing five atoms. The contribution of H atoms in metal hydrides usually manifests at substantially higher temperatures, following the high energy of H optical modes.
Low-temperature specific heat (Figure 8) exhibits an upturn in C/T(T). In principle, it could be related to the nuclear specific heat of Yb. There exist two Yb isotopes having nuclear spin, 171Yb with I = ½ and 173Yb with I = 5/2 [44]. However, the measured data (Figure 7) do not follow the 1/T2 behavior typical for nuclear contribution CN. This fact suggests that a term of another origin can contribute, if not dominate, in the low-temperature range (e.g., certain magnetic interactions). A detailed view shows a shoulder at T ≈ 2 K followed by another rapid increase on its low-temperature side. The upturn exists already in Yb2Pd2Sn, but it is much more pronounced in its hydride and the experimental C/T value for T → 0 extrapolation is enormous, ≈1.8 J/mol f.u. K2, i.e., more than twice higher than in its precursor. The data do not identify any magnetic phase transition down to ≈500 mK. Measurements in magnetic fields reduce the values only partly, and a broad maximum develops gradually. This excludes a static disorder as a source of high C/T values; in such case, the field suppression would be much faster. Instead, it points to the influence of spin fluctuations similar to U2Co2InH1.9 [45] or U2Co2Sn [46]. The observed shift of magnetic entropy towards higher temperatures could be, in principle, a fingerprint of ferromagnetism, but that is excluded by negative θp values. The shift of the C/T data to the higher temperatures with the application of the magnetic field can also arise from the Schottky anomaly appearing at higher temperatures.
The situation is complicated by the fact that Yb2O3 (which might be present in the sample—although not detected by XRD) shows a peak of magnetic origin [47] in the vicinity of the upturn present.
In addition to the upturn, the low-temperature part can be tentatively described by the Debye model (Figure 9) with the Debye temperature θD = 210 K and the electronic term γ × T, with γ = 180 mJ/mol f.u. K2 (green line in Figure 9). For the low-temperature analysis, it is appropriate to use the Debye model with five atoms in formula unit. Vibrations of additional H atoms usually contribute to the lattice specific heat by high-energy optical modes, which are not populated far below 300 K. The fast reduction in γ with increasing T is a common attribute of Kondo systems, in which the enhanced γ-values mean low characteristic temperatures, below which the condensation into Kondo singlet happens. At higher temperatures, the Kondo resonance in the quasiparticle density of states is lost [48], e.g., in CeAl3, the γ-value drops into rather usual values [49]. However, the Debye model should be taken with caution as it fails for temperatures above 50 K; in addition, crystal-field splitting and its contribution to the specific heat is not taken into account.
Materials in a valence-fluctuating regime usually exhibit lower γ-values than Kondo materials as the quasiparticle resonance at the Fermi level is broadened by charge fluctuations.

3. Discussion

We showed that the hydride of Yb2Pd2Sn could be synthesized with approximately 2 H atoms per f.u. The lattice reaction is strongly anisotropic, and the 5% expansion in c is partly compensated by the 0.5% compression in a. For example, the Yb–Yb distances remain practically the same.
Placing the hydride into the systematics of analogous rare-earth materials, it is evident that Yb remains at or very close to the 3+ (4f13) state. However, it remains paramagnetic at least down to 0.5 K. The low-temperature upturn in C/T(T) is practically doubled in the hydride, giving the very high γ-value of almost 2 J/mol f.u. K2, indicating a Kondo regime of the 4f shell. In the past, very high γ-values were identified, e.g., for Ce-based “221”compounds [50].
The difference between Yb2Pd2Sn and its hydride can be understood as a result of interplay of the lattice changes and H effect on the bonding, with the latter affecting mainly electronic states of Yb. Generally, the volume expansion would prefer less stable 4f moments, as the divalent Yb is much larger than the trivalent one. In Yb2Pd2Sn, the distance to two nearest Yb neighbors (equivalent to c) indeed expands upon hydrogenation; however, the distances within the basal plane remain practically the same in the hydride. The nearest neighbors become those within the Yb–Yb basal-plane dimers.
On the other hand, we assume an important bonding of the Yb-5d and 6s states with the H-1s states [27], which reduces the density of states at the Fermi level, and the 4f13 state may become more stable. The 4d states of Pd which is adjacent to H are likely to be filled in the precursor intermetallic already due to the high Pd electronegativity. The intersite exchange interaction becomes consequently weaker. Apparently, the result is a decrease in the Kondo temperature, which makes the Kondo effect more apparent; the γ-coefficient increases. The long-range order at still lower temperatures cannot be, however, excluded.
A tendency to magnetic order can, in addition, be negatively affected by a lattice disorder. In addition, the usual disorder due to incomplete occupation of the H sublattice as the H occupancy can be slightly below 2/f.u., and there is the specific feature of the Mo2FeB2 structure type, offering a stochastic occupation of 50% of equivalent H sites. Such a situation was found to have an important impact on properties of isostructural U compounds [51].

4. Materials and Methods

A standard procedure of hydrogenation was performed. A single-phase polycrystalline sample of Yb2Pd2Sn was crushed into a coarse-grained powder. In order to remove surface contaminants, the powder was heated to T = 523 K in a dynamic vacuum (10−6 mbar). Subsequently, it underwent thermal treatments in hydrogen atmosphere. First, the hydrogenation was performed at hydrogen pressure of 0.6 bar by heating up to T ≈ 523 K. No significant hydrogen absorption was observed. However, a hydrogen absorption was achieved at H2 pressure of 100 bar by heating up to T ≈ 473 K and subsequent cooling with the rate 0.1 K/min. The amount of hydrogen absorbed was determined by thermally induced desorption in a closed volume, giving the value (1.8 ± 0.2) H at./f.u., analogous to other R2T2X hydrides which preserve the tetragonal symmetry [30]. The powder X-ray diffraction was employed to determine the crystal structure and quality of the prepared sample. The Fullprof package (Version: May 2016) [52] was used to treat the data.
Quantum Design PPMS equipment was used for magnetic studies and heat-capacity measurements. The grains of the sample for magnetic measurement were fixed in random orientation by acetone-soluble glue. Magnetic measurements of Yb2Pd2SnH≈2 were performed in the temperature range 2–300 K and fields up to 14 T. The specific heat was measured down to 0.4 K in external magnetic fields up to 5 T using the 3He insert for PPMS on a pellet prepared by pressing the powder in the case of the hydride.

Author Contributions

S.M.-C.: conceptualization, investigation, writing—original draft, writing—review and editing, visualization, and validation; E.B.: investigation and resources; M.G.: investigation and resources; L.H.: conceptualization, investigation, resources, writing—original draft, writing—review and editing, supervision, and validation. All authors have read and agreed to the published version of the manuscript.

Funding

The work was supported by the Czech Science Foundation under the grant No. 21-09766S. Experiments were performed in MGML, which is supported within the Program of Czech Research Infrastructures (project no. LM2018096).

Data Availability Statement

All data will be made available upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Maiwald, J.; Mazin, I.; Gurevich, A.; Aronson, M. Superconductivity in La2Ni2In. Phys. Rev. B 2020, 102, 165125. [Google Scholar] [CrossRef]
  2. Dudka, A.; Nesterenko, S.; Tursina, A. Multi-temperature X-ray diffraction study of a reversible structural phase transition in the high-temperature polymorph of Ce2Rh2Ga compound. J. Alloys Compd. 2021, 890, 161759. [Google Scholar] [CrossRef]
  3. Sahu, B. Structural, magnetic, thermodynamic and electrical transport properties of a new compound Pr2Rh2Ga. arXiv 2021, arXiv:2102.04106. [Google Scholar]
  4. Menouer, S.; Abid, O.; Benzair, A.; Yakoubi, A.; Khachai, H.; Schwingenschlögl, U. First principles calculations of the structural, electronic, magnetic, and thermodynamic properties of the Nd2MgGe2 and Gd2MgGe2 intermetallic compounds. Sci. Rep. 2021, 11, 10870. [Google Scholar] [CrossRef]
  5. Zhang, Y. Review of the structural, magnetic and magnetocaloric properties in ternary rare earth RE2T2X type intermetallic compounds. J. Alloys Compd. 2019, 787, 1173. [Google Scholar] [CrossRef]
  6. Li, L.; Mi, Y. Recent progresses in exploring the rare earth based intermetallic compounds for cryogenic magnetic refrigeration. J. Alloys Compd. 2020, 823, 153810. [Google Scholar] [CrossRef]
  7. Nesterenko, S.N.; Tursina, A.I.; Kuznetsov, A.N. Extending interstitial tetrelides into carbides: Synthesis and crystal and electronic structures- of RE2Co2AlC (RE = La, Pr, Nd). Dalton Trans. 2023, 52, 11611. [Google Scholar] [CrossRef]
  8. Reimann, M.K.; Matar, S.F.; Pöttgen, R. Intermetallic compounds RE2Ga2Mg (RE = Tb-Tm, Lu) with Mo2B2Fe-type structure. Z. Für Naturforschung B 2022, 77, 693–702. [Google Scholar] [CrossRef]
  9. Lukachuk, M.; Pöttgen, R. Intermetallic compounds with ordered U3Si2 or Zr3Si2 type structure—Crystal chemistry, chemical bonding and physical properties. Z. Kristallogr. 2003, 218, 767–787. [Google Scholar] [CrossRef]
  10. Shastry, B.; Sutherland, B. Exact ground state of a quantum mechanical antiferromagnet. Physica B+C 1981, 108, 1069–1070. [Google Scholar] [CrossRef]
  11. Shimura, Y.; Sakakibara, T.; Iwakawa, K.; Sugiyama, K.; Onuki, Y. Low temperature magnetization of Yb2Pt2Pb with the Shastry-Sutherland type lattice and a high-rank multipole interaction. J. Phys. Soc. Jpn. 2012, 81, 103601. [Google Scholar] [CrossRef]
  12. Wu, L.S.; Gannon, W.J.; Zaliznyak, A.I.; Tsvelik, A.M.; Brockmann, M.; Caux, J.S.; Kim, M.S.; Qiu, Y.; Copley, J.R.D.; Ehlers, G.; et al. Orbital-exchange and fractional quantum number excitations in an f-electron metal, Yb2Pt2Pb. Science 2016, 352, 1206–1210. [Google Scholar] [CrossRef]
  13. Sereni, J.G.; Gómez Berisso, M.; Braghta, A.; Schmerber, G.; Kappler, J.P. Unstable Shastry-Sutherland phase in Ce2Pd2Sn. Phys. Rev. B 2009, 80, 024428. [Google Scholar] [CrossRef]
  14. Kim, M.S.; Aronson, M.C. Spin Liquids and Antiferromagnetic Order in the Shastry-Sutherland-Lattice Compound Yb2Pt2Pb. Phys. Rev. Lett. 2013, 110, 017201. [Google Scholar] [CrossRef]
  15. Kim, M.S.; Bennett, M.C.; Aronson, M.C. Yb2Pt2Pb: Magnetic frustration in the Shastry-Sutherland lattice. Phys. Rev. B 2008, 77, 144425. [Google Scholar] [CrossRef]
  16. Sahu, B.; Djoumessi, R.; Strydom, A. Spin-glass behavior in Shastry-Sutherland lattice of Tm2Cu2In. J. Magn. Magn. Mat. 2021, 543, 168599. [Google Scholar] [CrossRef]
  17. Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
  18. Mašková, S.; Havela, L.; Kolomiets, A.; Miliyanchuk, K.; Andreev, A.V.; Nakotte, H.; Peterson, J.; Skourski, Y.; Yasin, S.; Zherlitsyn, S.; et al. Onset of magnetic order in U2(Ni1-xFex)2Sn-H. J. Korean Phys. Soc. 2013, 62, 1542–1546. [Google Scholar] [CrossRef]
  19. Maskova, S.; Chotard, J.-N.; Denys, R.V.; Miliyanchuk, K.; Yartys, V.; Giovannini, M.; Akselrud, L.; Halevy, I.; Prokleska, J.; Havela, L. Nd2Ni2MgH8 hydride: Synthesis, structure and magnetic properties. Intermetallics 2017, 87, 13–20. [Google Scholar] [CrossRef]
  20. Muramatsu, T.; Kanemasa, T.; Kagayama, T.; Shimizu, K.; Aoki, Y.; Sato, H.; Giovannini, M.; Bonville, P.; Zlatic, V.; Aviani, I.; et al. Reentrant quantum criticality in Yb2Pd2Sn. Phys. Rev. B 2011, 83, 180404. [Google Scholar] [CrossRef]
  21. Bauer, E.; Khan, R.T.; Giovannini, M.; Ritter, C. Appearance of long range magnetic order in a nonmagnetic periphery: Yb2Pd2(In,Sn). Phys. Status Solidi B 2010, 247, 717–719. [Google Scholar] [CrossRef]
  22. Ruderman, M.A.; Kittel, C. Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
  23. Kong, B.; Zhang, L.; Chen, X.-R.; Deng, M.-S.; Cai, L.-C.; Ling-Hu, R.-F. Magnetic, electronic and optical properties of lanthanide hydrides, GdH2 and GdH3. J. Phys. Chem. Solids 2013, 74, 1322–1328. [Google Scholar] [CrossRef]
  24. Carlin, R.L.; Chirico, R.D.; Joung, K.O.; Shenoy, G.K.; Westlake, D.G. Magnetic ordering in GdH3. Phys. Lett. A 1980, 75, 413–414. [Google Scholar] [CrossRef]
  25. Huiberts, J.N.; Griessen, R.; Rector, J.H.; Wijngaarden, R.J.; Dekker, J.P.; De Groot, D.G.; Koeman, N.J. Yttrium and lanthanum hydride films with switchable optical properties. Nature 1996, 380, 231–234. [Google Scholar] [CrossRef]
  26. Fuggle, J.C.; Hillebrecht, F.U.; Zeller, R.; Zołnierek, Z.; Bennett, P.A.; Freiburg, C. Electronic structure of Ni and Pd alloys. I. X-ray photoelectron spectroscopy of the valence bands. Phys. Rev. B 1983, 27, 2145–2178. [Google Scholar] [CrossRef]
  27. Havela, L. Hydrogen impact on magnetic properties of metallic systems. J. Alloys Compd. 2022, 895, 162721. [Google Scholar] [CrossRef]
  28. Javorsky, P.; Tuan, N.C.; Divis, M.; Havela, L.; Svoboda, P.; Sechovsky, V.; Hilscher, G. Magnetic properties of RCuAl and RNiAl compounds. J. Magn. Magn. Mat. 1995, 140–144, 1139–1140. [Google Scholar] [CrossRef]
  29. Gaudin, E.; Matar, S.F.; Pottgen, R.; Eul, M.; Chevalier, B. Drastic Change of the Ferromagnetic Properties of the Ternary Germanide GdTiGe through Hydrogen Insertion. Inorg. Chem. 2011, 50, 11046–11054. [Google Scholar] [CrossRef]
  30. Mašková, S.; Kolomiets, A.; Havela, L.; Andreev, A.V.; Svoboda, P. Impact of hydrogen absorption on crystal structure and magnetic properties of RE2T2X compounds. J. Alloys Compd. 2015, 645, S76–S79. [Google Scholar] [CrossRef]
  31. Chevalier, B.; Gaudin, E.; Tencé, S.; Malaman, B.; Fernandez, J.R.; André, G.; Coqblin, B. Hydrogenation Inducing Antiferromagnetism in the Heavy-Fermion Ternary Silicide CeRuSi. Phys. Rev. B 2008, 77, 014414. [Google Scholar] [CrossRef]
  32. Iwasieczko, W.; Kazorowski, D. Influence of hydrogen absorption on structural and magnetic properties of Ce2Ni2In. J. Alloys Compd. 2010, 507, 376–379. [Google Scholar] [CrossRef]
  33. Chevalier, B.; Matar, S.F.; Ménétrier, M.; Sanchez Marcos, J.; Rodriguez Fernandez, J. Influence of Ce-H bonding on the physical properties of the hydrides CeCoSiH(1.0) and CeCoGeH(1.0). J. Phys. Condens. Matter 2006, 18, 6045–6056. [Google Scholar] [CrossRef] [PubMed]
  34. Iwasieczko, W.; Kazorowski, D. Hydrogen insertion effect on the magnetic properties of Ce2Pd2In. J. Alloys Compd. 2011, 509, 1384–1388. [Google Scholar] [CrossRef]
  35. Iwasieczko, W.; Kazorowski, D. Hydrogenation studies on structural and magnetic properties of antiferromagnetic Kondo lattice Ce2Cu2In. J. Alloys Compd. 2013, 553, 364–366. [Google Scholar] [CrossRef]
  36. Drulis, M.K.; Drulis, H. Double Kondo-lattice-like system in the ytterbium deuterides. J. Alloys Compd. 2004, 366, 9–14. [Google Scholar] [CrossRef]
  37. Warf, J.C.; Hardcastle, K.J. Rare Earth-Hydrogen Systems. IV. The Higher Hydride of Ytterbium, a New Type of Hydride. Inorg. Chem. 1966, 5, 1736–1740. [Google Scholar] [CrossRef]
  38. Iwasieczko, W.; Drulis, M.; Drulis, H. Magnetic properties of the ytterbium non-stoichiometric trihydride phase. J. Alloys Compd. 1997, 259, 62–64. [Google Scholar] [CrossRef]
  39. Aoki, Y.; Sato, H.R.; Sugawara, H.; Sato, H. Anomalous magnetic properties of Heusler superconductor YbPd2Sn. Phys. C Supercond. 2000, 333, 187–194. [Google Scholar] [CrossRef]
  40. Dönni, A.; Fischer, P.; Fauth, F.; Convert, P.; Aoki, Y.; Sugawara, H.; Sato, H. Antiferromagnetic ordering in the cubic superconductor YbPd2Sn. Phys. B 1999, 259–261, 705–706. [Google Scholar] [CrossRef]
  41. Shoemaker, D.P.; Shoemaker, C.B. Concerning atomic sites and capacities for hydrogen absorption in the AB2 Friauf-Laves phases. J. Less-Common Met. 1979, 68, 43–58. [Google Scholar] [CrossRef]
  42. Maskova-Cerna, S.; Kolomiets, A.; Prchal, J.; Halevy, I.; Buturlim, V.; Nikolaevsky, M.; Koloskova, O.; Kozelj, P.; König, M.; Divis, M.; et al. Insight into the physics of the 5f -band antiferromagnet U2Ni2Sn from the pressure dependence of crystal structure and electrical resistivity. Phys. Rev. B 2021, 103, 035104. [Google Scholar] [CrossRef]
  43. van den Berg, G.J. Magnetism—Selected Topic; Foner, S., Ed.; Gordon and Breach Science Publishers: New York, NY, USA, 1976; pp. 117–172. [Google Scholar]
  44. Steppke, A.; Brando, M.; Oeschler, N.; Krellner, C.; Geibel, C.; Steglich, F. Nuclear contribution to the specific heat of Yb(Rh0.93Co0.07)2Si2. Phys. Status Solidi B 2010, 247, 737–739. [Google Scholar] [CrossRef]
  45. Havela, L.; Miliyanchuk, K.; Kolomiets, A. f-Element hydrides: Structure and magnetism. Int. J. Mat. Res. 2009, 100, 1182–1186. [Google Scholar] [CrossRef]
  46. Kim, J.S.; Alwood, J.; Getty, S.A.; Sharifi, F.; Stewart, G.R. U2Co2Sn: An undoped non-Fermi-liquid system with Ce ≈ γ − A√T. Phys. Rev. B 2000, 62, 6986–6990. [Google Scholar] [CrossRef]
  47. Rojas, D.P.; Espeso, J.I.; Rodríguez Fernández, L.; Fernández Barquín, L. Heat capacity of nanocrystalline Yb2O3. Ceram. Int. 2022, 48, 879–886. [Google Scholar] [CrossRef]
  48. Bickers, N.E.; Cox, D.L.; Wilkins, J.W. Self-consistent large-N expansion for normal-state properties of dilute magnetic alloys. Phys. Rev. B 1987, 36, 2036–2079. [Google Scholar] [CrossRef]
  49. Brodale, G.E.; Fisher, R.A.; Philips, N.E.; Fouquet, J. Pressure dependence of the low-temperature specific heat of the heavy-fermion compound CeAl3. Phys. Rev. Lett. 1986, 56, 390–393. [Google Scholar] [CrossRef] [PubMed]
  50. Sudhindra, R.; Poettgen, R. Antiferromagnetic ordering in the heavy-fermion system Ce2Au2Cd. Phys. Rev. B 2005, 72, 214435. [Google Scholar]
  51. Sandratskii, L.M.; Havela, L. Microscopic nature of drastic influence of hydrogen on the magnetic anisotropy of 5f-electron system. Phys. Rev. B 2020, 101, 100409. [Google Scholar] [CrossRef]
  52. Rodriguez-Carvajal, J. Recent developments of the program FULLPROF. Comm. Powder Diffr. IUCr Newsl. 2001, 26, 12–19. [Google Scholar]
Inorganics 11 00414 g001
Figure 1. (a). Shastry–Sutherland lattice as suggested in [10]; (b) Mo2FeB2 structure showing Yb atoms. The inter-dimer and intra-dimer interactions are indicated; (c) Mo2FeB2 structure showing Yb atoms (grey). Superposed is a schematic representation of a square lattice built up from the Yb dimers (orange).
Figure 1. (a). Shastry–Sutherland lattice as suggested in [10]; (b) Mo2FeB2 structure showing Yb atoms. The inter-dimer and intra-dimer interactions are indicated; (c) Mo2FeB2 structure showing Yb atoms (grey). Superposed is a schematic representation of a square lattice built up from the Yb dimers (orange).
Inorganics 11 00414 g001
Inorganics 11 00414 g002
Figure 2. XRD pattern (Cu Kα radiation) of Yb2Pd2Sn (simulated) compared to its hydride. The green ticks show the position of diffraction peaks of YbPd2Sn impurity.
Figure 2. XRD pattern (Cu Kα radiation) of Yb2Pd2Sn (simulated) compared to its hydride. The green ticks show the position of diffraction peaks of YbPd2Sn impurity.
Inorganics 11 00414 g002
Inorganics 11 00414 g003
Figure 3. Relative lattice changes upon hydrogenation of the lattice parameters a and c (Δa/a and Δc/c, respectively) along the RE series [30]. In and Sn compounds are marked as black and red columns, respectively. Yb2Pd2Sn is shown as hatched columns (4f13 as red, hypothetical 4f14 as green).
Figure 3. Relative lattice changes upon hydrogenation of the lattice parameters a and c (Δa/a and Δc/c, respectively) along the RE series [30]. In and Sn compounds are marked as black and red columns, respectively. Yb2Pd2Sn is shown as hatched columns (4f13 as red, hypothetical 4f14 as green).
Inorganics 11 00414 g003
Inorganics 11 00414 g004
Figure 4. Temperature dependence of magnetic susceptibility (a) and inverse magnetic susceptibility (b) of Yb2Pd2Sn compared to its hydride.
Figure 4. Temperature dependence of magnetic susceptibility (a) and inverse magnetic susceptibility (b) of Yb2Pd2Sn compared to its hydride.
Inorganics 11 00414 g004
Inorganics 11 00414 g005
Figure 5. Temperature dependence of magnetic susceptibility of Yb2Pd2SnH≈2 measured in various magnetic fields.
Figure 5. Temperature dependence of magnetic susceptibility of Yb2Pd2SnH≈2 measured in various magnetic fields.
Inorganics 11 00414 g005
Inorganics 11 00414 g006
Figure 6. Field dependence of magnetization (per f.u.) of Yb2Pd2SnH≈2 measured at T = 2 and 15 K compared to the corresponding Brillouin functions for 1 Yb atom (J = 7/2, gj = 8/7, gJ = 4) at various temperatures. One should be aware that 1 f.u. has 2 Yb atoms but the Brillouin functions here give the theoretical values for 1 Yb atom.
Figure 6. Field dependence of magnetization (per f.u.) of Yb2Pd2SnH≈2 measured at T = 2 and 15 K compared to the corresponding Brillouin functions for 1 Yb atom (J = 7/2, gj = 8/7, gJ = 4) at various temperatures. One should be aware that 1 f.u. has 2 Yb atoms but the Brillouin functions here give the theoretical values for 1 Yb atom.
Inorganics 11 00414 g006
Inorganics 11 00414 g007
Figure 7. Temperature dependence of the specific heat (in the C/T vs. T representation) of Yb2Pd2Sn compared to its hydride.
Figure 7. Temperature dependence of the specific heat (in the C/T vs. T representation) of Yb2Pd2Sn compared to its hydride.
Inorganics 11 00414 g007
Inorganics 11 00414 g008
Figure 8. Low-T detail of the temperature dependence of the specific heat (in the C/T vs. T representation) for Yb2Pd2SnH≈2 measured in various magnetic fields. The inset shows the temperature dependence of the specific heat in zero field using a logarithmic scale.
Figure 8. Low-T detail of the temperature dependence of the specific heat (in the C/T vs. T representation) for Yb2Pd2SnH≈2 measured in various magnetic fields. The inset shows the temperature dependence of the specific heat in zero field using a logarithmic scale.
Inorganics 11 00414 g008
Inorganics 11 00414 g009
Figure 9. Debye fit of the specific heat (in the C/T vs. T representation) for Yb2Pd2SnH≈2. The green line represents the Debye fit for ΘD = 210 K and γ = 180 mJ/mol f.u. K2.
Figure 9. Debye fit of the specific heat (in the C/T vs. T representation) for Yb2Pd2SnH≈2. The green line represents the Debye fit for ΘD = 210 K and γ = 180 mJ/mol f.u. K2.
Inorganics 11 00414 g009
Table 1. Structure parameters of Yb2Pd2Sn [20] and its hydride. Lattice parameters a and c, unit cell volume V, relative lattice expansion along a direction Δa/a, along c direction Δc/c, and relative volume expansion ΔV/V are given. Notice that the refined atomic coordinates determining the position of the Yb and Pd in crystal lattice change only very little.
Table 1. Structure parameters of Yb2Pd2Sn [20] and its hydride. Lattice parameters a and c, unit cell volume V, relative lattice expansion along a direction Δa/a, along c direction Δc/c, and relative volume expansion ΔV/V are given. Notice that the refined atomic coordinates determining the position of the Yb and Pd in crystal lattice change only very little.
Yb2Pd2SnYb2Pd2SnH≈2
a (Å)7.5807.544 (2)
c (Å)3.6393.820 (1)
V (Å3)209.1217.4 (1)
∆a/a (%)-−0.47
∆c/c (%)-4.97
∆V/V (%)-3.97
Atomic positionsYb(0.1724, 0.6724, 0.5)(0.1712 (4), 0.6712 (4), 0.5)
Pd(0.3716, 0.8716, 0)(0.3699 (5), 0.8699 (5), 0)
Sn(0, 0, 0)(0, 0, 0)
Shortest basal-plane dYb-Yb (Å)3.6963.653
c-axis dYb-Yb (Å)3.6393.8197
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Maskova-Cerna, S.; Bauer, E.; Giovannini, M.; Havela, L. Heavy-Fermion Properties of Yb2Pd2SnH≈2. Inorganics 2023, 11, 414. https://doi.org/10.3390/inorganics11100414

AMA Style

Maskova-Cerna S, Bauer E, Giovannini M, Havela L. Heavy-Fermion Properties of Yb2Pd2SnH≈2. Inorganics. 2023; 11(10):414. https://doi.org/10.3390/inorganics11100414

Chicago/Turabian Style

Maskova-Cerna, Silvie, Ernst Bauer, Mauro Giovannini, and Ladislav Havela. 2023. "Heavy-Fermion Properties of Yb2Pd2SnH≈2" Inorganics 11, no. 10: 414. https://doi.org/10.3390/inorganics11100414

APA Style

Maskova-Cerna, S., Bauer, E., Giovannini, M., & Havela, L. (2023). Heavy-Fermion Properties of Yb2Pd2SnH≈2. Inorganics, 11(10), 414. https://doi.org/10.3390/inorganics11100414

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop