Next Article in Journal
Release of Pure H2 from Na[BH3(CH3NH)BH2(CH3NH)BH3] by Introduction of Methyl Substituents
Next Article in Special Issue
Revealing the Minimum Energy Pathways for Formamide Hydrogenation Reactions in the Presence of Platinum and Platinum–Vanadium Clusters: A Quantum Chemical DFT/Nudged Elastic Band Study
Previous Article in Journal
Calcium-Based Sorbent Carbonation at Low Temperature via Reactive Milling under CO2
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 11
Issue 5
10.3390/inorganics11050201
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Insight on the Formation Mechanism of a Trisubstituted Derivative of Closo-Decaborate Anion [B10H7O2CCH3(NCCH3)]0

by
Ilya N. Klyukin
1,*,
Anastasia V. Kolbunova
1,
Alexander S. Novikov
2,3,4,*,
Andrey P. Zhdanov
1,
Konstantin Yu. Zhizhin
1 and
Nikolay T. Kuznetsov
1
1
Kurnakov Institute of General and Inorganic Chemistry, Russian Academy of Sciences, Leninskii pr., 31, 117907 Moscow, Russia
2
Institute of Chemistry, Saint Petersburg State University, Universitetskaya nab. 7-9, 199034 Saint Petersburg, Russia
3
Research Institute of Chemistry, Peoples’ Friendship University of Russia (RUDN University), Miklukho-Maklaya st. 6, 117198 Moscow, Russia
4
Infochemistry Scientific Center, ITMO University, Kronverksky pr., 49, bldg. A, 197101 Saint Petersburg, Russia
*
Authors to whom correspondence should be addressed.
Inorganics 2023, 11(5), 201; https://doi.org/10.3390/inorganics11050201
Submission received: 8 April 2023 / Revised: 3 May 2023 / Accepted: 4 May 2023 / Published: 6 May 2023
(This article belongs to the Special Issue Experimental and Theoretical Studies of Main and Transition Group Elements Cluster Compounds)
Browse Figures
Versions Notes

Abstract

:
A theoretical modelling of the interaction process between a protonated complex of carboxonium derivative [2,6-B10H8O2CCH3*Hfac]0 and acetonitrile molecule CH3CN was carried out. As a result of the process, a trisubstituted [B10H7O2CCH3(NCCH3)]0 derivative was formed. This reaction has an electrophile-induced nucleophilic substitution (EINS) mechanism. The main intermediates and transition states of the substitution process were established. As in the case of all previously investigated EINS processes, the key intermediate was an anion with a dihydrogen H2 fragment attached to one boron atom (B(H2) structure motif). The process of nucleophilic substitution can proceed on a different position of the cluster cage. The main potential pathways were assessed. It was established that substitution on the B4 position of the cluster cage was the most energetically favourable, and the [2,4,6-B10H7O2CCH3(NCCH3)]0 isomer was formed.

Graphical Abstract

1. Introduction

Closo-borate anions [BnHn]2− n = 6–12 are versatile building blocks for creating molecular platforms, with a plethora of useful applications in medicine, electrochemistry, magnetic materials, etc. [1,2,3,4,5]. The main approach for the formation of such platforms is the process of the substitution of a hydrogen atom to create different exo-polyhedral substituents [6,7,8,9,10]. Thus, investigation of the substitution process in closo-borate anions is one of the central cornerstones of modern chemistry in relation to boron clusters [11,12,13,14].
The process of substitution of exo-polyhedral hydrogen atoms can be achieved by different mechanisms, such as nucleophilic, electrophilic and radical substitution of exo-polyhedral hydrogen atoms [15,16,17,18,19,20]. To date, the most commonly investigated mechanism has been electrophile-induced nucleophilic substitution (EINS) [21,22,23]. Various classes of organic molecules, such as ethers, esters and nitriles, can act as nucleophiles in EINS processes [23,24,25]. Brønsted and Lewis acids can act as an electrophile inducer [26,27]. For closo-decaborate anions, the most common inducers are CF3COOH and CF3SO3H. The mechanism of the EINS process has been described in detail in several articles [28,29,30]. This process involves several steps. The first step is the protonation of the boron cluster, with the formation of [BnHn(Hfac)]−. Depending on the nature of the cluster, the proton can be localised on one facet, or it can transfer through one of the equatorial belts. In the next step, Hfac migrates with the formation of a key intermediate with the general form [BnHn−1H2]−. In the following step, a H2 molecule is eliminated and a [BnHn−1]− intermediate is formed. In this intermediate, one of the boron atoms has a vacant orbital, which makes this intermediate highly reactive. In the final step, this intermediate interacts with a molecule of the nucleophile Nu, with the formation of the target product [BnHn−1Nu]−.
Depending on the type of electrophile inducer and nucleophile molecule, it is possible to vary the degree of substitution introduced into the boron cluster cage. The introduction of several substituents to the cluster cage allows one to design multifunctional borylated platforms. Previously, several disubstituted derivatives of closo-borate anions have been investigated. Disubstituted oxonium and nitrilium derivative were obtained on the basis of interactions between closo-decaborate anions [B10H10]2− and ethers or nitriles, in the presence of trifluoromethanic acid CF3SO3H as an electrophile inducer [31,32].
Is it possible to obtain a trisubstituted product on the basis of the EINS process? To answer this question, it was decided to focus on carboxonium derivatives of closo-borate anions with the general form [B10H8O2CR]−. The given type of anions is disubstituted and have a total charge equal to −1. Thus, it is possible to introduce an additional isomer to these systems on the basis of the EINS process. Currently, these derivatives are actively studied and can be obtained on the basis of the interaction between [B10H11]− and carboxylic acid [33]. The mechanism of formation of a disubstituted derivative was established on the basis of the formation of [B10H8O2CC6H5]− [34]. This process involves the EINS mechanism and goes through the formation of [B10H9H2]−. After H2 elimination, a monosubstituted derivative of the general form [B10H9OC(OH)R]− is formed. This derivative undergoes intermolecular cyclisation and finally [B10H8O2CC6H5]− is formed. In addition, the process of protonation of [B10H8O2CCH3]− was investigated [35]. Trifluoromethansulphonic acid, CF3SO3H, was used as an electrophile inducer. In contrast to the unsubstituted [B10H11]− anion, in the case of [2,6-B10H8O2CCH3*Hfac]0, the additional proton did not migrate along the equatorial belt and was localised on the boron cage facet opposite the B atoms associated with the exo-polyhedral substitution.
Thus, in the present study, the DFT modelling of the interaction between [2,6-B10H8O2CCH3*Hfac]0 and a molecule of acetonitrile CH3CN was performed. As a result of the given process, a trisubstituted [B10H7O2CCH3(NCCH3)]0 derivative was formed. Such a derivative was chosen due to its wide range of possibilities for further modification. The nitrilium group attached to the boron cluster moiety can react with various nucleophiles. The [B10H7O2CCH3(NCCH3)]0 derivative can be applied for the formation of a molecular platform with specific properties.

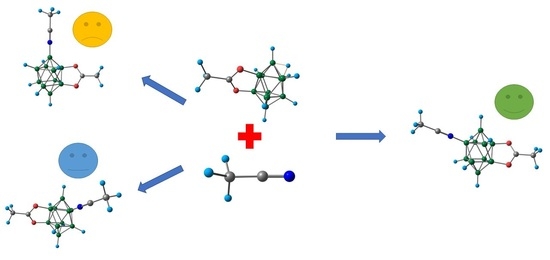
2. Results and Discussion

The closo-decaborate anion [B10H10]2− has two types of boron atom: apical and equatorial. When an additional substituent is introduced into the cluster cage, the equatorial atoms become nonequivalent. Substitution of the exo-polyhedral hydrogen atom can be carried out at different positions of the cluster cage. Thus, in the course of this work, different pathways of the substitution process were calculated. In addition, a comparison of the process of substitution of the hydrogen atom in [B10H8O2CCH3(Hfac)]0 and for the unsubstituted [B10H11]− species was carried out. Optimisation of geometries and calculation of Hessian matrices were carried out at the wB97X-D3/def2-TZVPP level. In addition, for a more accurate evaluation of energetic parameters for all equilibria geometries, single-point DLPNO-CCSDT/cc-pvdz calculations were performed. All calculations were performed in dichloromethane CH2Cl2 media, in order to approximate the conditions of theoretical modelling to the real experimental conditions. Dichloromethane was chosen as the solvent, since it does not react with the closo-borate anions and the results obtained in this work can be used for comparison with other types of nucleophiles.
As stated in the authors’ previous work [35], in the most stable isomer of [B10H8O2CCH3(Hfac)]0 an additional proton, Hfac, is localised on the facet opposite the substituted boron atom. Hfac attaches mainly to the apical boron atom and the B3 equatorial boron atom (Figure 1). Thus, this isomer of [B10H8O2CCH3(Hfac)]0 was considered in the present work and was chosen as the starting point for mechanism calculation. The sum of the energy of [B10H8O2CCH3(Hfac)]0 and CH3CN was accepted as the reference point and the relative Gibbs energy was equal to 0 kJ/mol.
The first step of nucleophilic substitution in [B10H8O2CCH3(Hfac)]− is proton migration, with the formation of [B10H7O2CCH3(H2)]−. The process of proton migration occurred through the formation of a transition state, as in the case of anion [B10H11]− [28,34]. Hfac can migrate to three different boron atoms: two equatorial boron atoms and one apical boron atom. Thus, three possible pathways of proton migration are possible (TSmigr_B1, TSmigr_B3, TSmigr_B4). The geometric parameters for all transition states are similar. The main structure feature is the coordination of two hydrogen atoms to one boron atom (Figure 2). The B-H bond distance was in the range of 1.22–1.23 Å for all isomers. The distance between the two hydrogen atoms was equal to 1.13 Å in the case of TSmigr_B3 equatorial isomers, 1.16 Å in case of TSmigr_B4 and 1.21 A in case of TSmigr_B1. However, the transition states had energy differences. The transition state in which the proton migrates to the B4 boron atom (TSelim_B4) had the lowest energy barrier (33.1 kJ/mol for wB97X-D3/def2-TZVPP and 43.6 kJ/mol for DLPNO-CCSDT/cc-pvdz). For the TSmigr_B3 transition state, the energy barrier was equal to 38.6 kJ/mol (wB97X-D3/def2-TZVPP) or 48.2 kJ/mol (DLPNO-CCSDT/cc-pvdz). The TSelim_B1 transition state in which the proton migrates to the apical boron atom had the highest energy barrier (46.6 kJ/mol for wB97X-D3/def2-TZVPP and 53.7 kJ/mol for DLPNO-CCSDT/cc-pvdz). Thus, analysing the energy profiles of possible pathways, one can conclude that the migration of hydrogen to the B4 atom was the most probable. It is noteworthy that, in the case of the [B10H11]− anion, the transition state energy barriers were higher than with the carboxonium derivative [B10H8O2CCH3(Hfac)]0. If the proton migrated to the equatorial boron atom (B10_TSmigr_eq), the energy barrier was equal to 59.1 kJ/mol for wB97X-D3/def2-TZVPP or 68.2 kJ/mol for DLPNO-CCSDT/cc-pvdz. In the case of migration to an apical position (B10_TSmigr_ap), the energy barrier was equal to 49.1 kJ/mol for wB97X-D3/def2-TZVPP or 57.2 kJ/mol for DLPNO-CCSDT/cc-pvdz.
Proton migration led to the formation of an intermediate in which the dihydrogen H2 fragment coordinated to one boron atom of the cluster cage. The nature of the interaction between the boron atom and the H2 fragment has been discussed in detail in several articles [28,29]. As in the case of transition state structures, the anion [B10H7O2CCH3(H2)]− has three possible isomers: H2_B1, H2_B3 and H2_B4 (Figure 3). For all isomers, the geometric parameters were quite similar. The distance between the hydrogen atoms was equal to 0.86–0.87 Å. The distance between a boron atom and a hydrogen atom was equal to 1.28–1.31 Å. The main geometric difference between transition state structures and [B10H7O2CCH3(H2)]− intermediates was the shortening of the H-H contacts and the broadening of the B-H contacts in an intermediate structure, compared with a transition state structure. It is noteworthy that the main geometric parameters were similar to analogous parameters in [B10H9(H2)]−; therefore, the nature of the introduced oxonium substituent had a slight effect on the bond parameters in the BH2 fragment. The isomer in which the H2 molecule was coordinated to the B4 atom (H2_B4) had a lower energy than the other isomers. The differences from the H2_B3 were 7.7 kJ/mol according to the wB97X-D3/def2-TZVPP calculation and 7.2 kJ/mol according to the DLPNO-CCSDT/cc-pvdz calculation. The isomer in which the dihydrogen fragment was coordinated with the apical boron atom H2_B1 had the highest relative energy. The differences between H2_B1 and H2_B4 were equal to 23.2 kJ/mol according to the wB97X-D3/def2-TZVPP calculation and 19.9 kJ/mol according to the DLPNO-CCSDT calculation. In the case of the [B10H9(H2)]− anion, the differences between the equatorial (B10_H2_eq) and apical isomers (B10_H2_ap) were equal to 11.6 kJ/mol using wB97X-D3/def2-TZVPP and 9.8 kJ/mol using DLPNO-CCSDT/cc-pvdz.
As in case of our previous study devoted to mechanism of formation of [B10H8O2CPh]−, the nature of B-H2 contact was investigated with the help of QTAIM formalism. Similar to the previously studied systems [B10H9H2] and [B10H8(OCOPh)H2], the analysis of the molecular graph of the of H2_B1, H2_B3 and H2_B4 revealed that the bond path from the boron atom was directed to the H-H bond centre (Figure 4). The B1_H2 isomer had the highest value of electron density at bond critical point (bcp) (Table S2). In addition, this isomer was characterized by the highest value of energy at bcp and the delocalization index. Thus, one can conclude that B1_H2 had the strongest covalent interaction between the boron atom and dihydrogen fragment. The B4_H2 isomer had the highest value of electron density at bcp devoted to the H-H interaction. This isomer was characterized by the highest value of energy at bcp and the delocalization index. B4_H2 isomer had the strongest covalent interaction between two hydrogen atoms in the H2 fragment.
In the next stage, the molecule of dihydrogen, H2, was eliminated through the formation of the transition state (TSelim_B1, TSelim_B3, TSelim_B4). These transition states had a significantly longer distance between the boron atom and the dihydrogen fragment (Figure 5). In the case of the elimination of the hydrogen molecule from a B3 boron atom (TSelim_B3), the distance between the boron atom and the hydrogen atoms of H2 lay in the range of 1.96–1.98 Å. In the case of TSelim_B4, the distance between the boron atom and the hydrogen atoms of H2 lay in the range of 2.19–2.21 Å. If the H2 molecule was eliminated from the boron atom in the apical position (TSelim_B1), the contact was the shortest, lying in the range of 1.73–1.74 Å. Additionally, the transition state was stabilised by an acetonitrile molecule. The elimination process had a significant energy barrier. TSelim_B4 had the lowest energy barrier: 145.2 kJ/mol (wB97X-D3/def2-TZVPP) and 109.5 kJ/mol (DLPNO-CCSDT/cc-pvdz). TSelim_B3 had a similar value, but it was higher: 151 kJ/mol (wB97X-D3/def2-TZVPP) and 115.1 kJ/mol (DLPNO-CCSDT/cc-pvdz). TSelim_B1 had the highest energy barrier values: 195.7 kJ/mol (wB97X-D3/def2-TZVPP) and 157.8 kJ/mol (DLPNO-CCSDT/cc-pvdz). Thus, the process of H2 molecule elimination most probably occurred from the B4 boron atom through the TSelim_B4 transition state. In the case of elimination from the equatorial boron atom of the [B10H9(H2)]− anion (B10_TSmigr_eq), the energy of the transition state was lower than that of the substituted carboxonium derivative. The relative Gibbs energies were equal to 139.9 kJ/mol (wB97X-D3/def2-TZVPP) and 104.2 kJ/mol (DLPNO-CCSDT/cc-pvdz). For elimination from the apical boron atom (B10_TSmigr_ap), the energy barrier was almost the same as in the case of the carboxonium derivative. The relative Gibbs energies were equal to 195.7 kJ/mol (wB97X-D3/def2-TZVPP) and 159.1 kJ/mol (DLPNO-CCSDT/cc-pvdz). Previously, an analogous calculation was carried out, and the energy barrier of hydrogen elimination was lower than in our case [36]. This discrepancy may be due to inaccuracies in the calculation scheme. In particular, all solvents have been explicitly accounted for. Our results are in good agreement with those obtained for hydrogen atom substitution for chlorine [28,29].
Finally, the target trisubstituted derivative was formed [B10H7O2CCH3(NCCH3)]0. For equatorial isomers [B10H7O2CCH3(NCCH3)]0 (Tris_B3 and Tris_B4), the B-N bond length was equal to 1.50 Å. For the apical isomer (Tris_B1), the B-N bond distance was equal to 1.47 Å. The CN bond distance was equal to 1.14 Å in all cases (Figure 6). These geometric parameters were very similar, or analogous, to the mono-substituted nitrilum derivative [B10H9NCCH3]−. The process of formation of a trisubstituted product was very exergonic. Tris_B4 had the most negative value of relative Gibbs energy. The overall Gibbs energy of the formation of the given isomer from [B10H8O2CCH3(Hfac)]0 and CH3CN was equal to −88.6 kJ/mol (wB97X-D3/def2-TZVPP) or −106.6 kJ/mol (DLPNO-CCSDT/cc-pvdz). The difference between Tris_B4 and Tris_B3 isomers was 5.1 kJ/mol according to the wB97X-D3/def2-TZVPP calculation or 5.64 kJ/mol according to the DLPNO-CCSDT/cc-pvdz calculation. Tris_B1 had the highest value of relative Gibbs energy. The difference between Tris_B1 and Tris_B4 was equal to 7.5 kJ/mol according to the wB97X-D3/def2-TZVPP calculation or 8.9 kJ/mol according to the DLPNO-CCSDT/cc-pvdz calculation. For monosubstituted nitrilium derivatives, the energy difference of apical [1-B10H9NCCH3]− and equatorial [2-B10H9NCCH3]− isomers was equal to 1 kJ/mol (wB97X-D3/def2-TZVPP) or 1.4 kJ/mol (to DLPNO-CCSDT/cc-pvdz).
In addition to geometric parameters, the bond orders of [B10H7O2CCH3(NCCH3)]0 isomers were calculated with the help of natural bond orbital (NBO) formalism. The Wiberg bond orders in Natural Atomic Orbital (NAO) basis for B–O interactions were equal to 0.70 (wB97X-D3/def2-TZVPP) and 0.57–0.58 (DLPNO-CCSDT/cc-pvdz). These values were similar for the initial carboxonium derivative [B10H8O2CCH3(Hfac)]0. In the case of initial [B10H8O2CCH3(Hfac)]0, the B–O bond orders were equal to 0.72 (wB97X-D3/def2-TZVPP) and 0.59 (DLPNO-CCSDT/cc-pvdz). The C–O bond orders for [B10H7O2CCH3(NCCH3)]0 isomers lay in the range of 1.30–1.31 (wB97X-D3/def2-TZVPP) and 1.20–1.22 (DLPNO-CCSDT/cc-pvdz). In the case of [B10H8O2CCH3(Hfac)]0, the C–O bond orders were equal to 1.30 (wB97X-D3/def2-TZVPP) and 1.21 (DLPNO-CCSDT/cc-pvdz). The B-N bond orders lay in the range of 0.81–0.83 (wB97X-D3/def2-TZVPP) and 0.57–0.58 (DLPNO-CCSDT/cc-pvdz). These values were similar to monosubstituted nitrilium derivatives with the general form [B10H9NCCH3]−. For monosubstituted nitrilium derivatives, the bond orders lay in the range 0.81–0.82 (wB97X-D3/def2-TZVPP) and 0.70–0.73 (DLPNO-CCSDT/cc-pvdz). The C≡N bond orders lay in the range of 2.58–2.60 (wB97X-D3/def2-TZVPP) and 2.54–2.55 (DLPNO-CCSDT/cc-pvdz). In the case of the analogous monosubstituted nitrilium derivative, the values of bond orders lay in the range of 2.59–2.60 (wB97X-D3/def2-TZVPP) and 2.56–2.57 (DLPNO-CCSDT/cc-pvdz). Thus, the main values of bond orders for trisubstituted derivatives were similar to the carboxonium derivative [B10H8O2CCH3(Hfac)]0 and nitrilium derivative [B10H9NCCH3]−.
The approach for preparation of the trisubstituted [B10H7O2CCH3(NCCH3)]0 derivative with exo-polyhedral nitrilium and carboxonium substituents was theoretically proposed. This approach was based on the EINS process. The protonated carboxonium derivative [B10H8O2CCH3(Hfac)]− can be used as the initial starting reagent. Such molecular species can interact with an acetonitrile molecule CH3CN with the formation of [B10H7O2CCH3(NCCH3)]0 derivatives. Three different pathways of hydrogen substitution to the nitrile molecule in [B10H8O2CCH3(Hfac)]− were considered (Figure 7 and Figures S1–S3). The most energetically favourable pathway was the substitution of the hydrogen atom at the boron atom at the B4 position. This route had the lowest energy of the [B10H7O2CCH3(H2)]− species and transition states of the elimination stage. The Tris_B4 isomer had the most energetically favourable pathway among the other isomers of [B10H7O2CCH3(NCCH3)]0 (Table 1). Comparing the energetic parameters for the formation of the trisubstituted derivative [B10H7O2CCH3(NCCH3)]0 and monosubstituted derivative [B10H9NCCH3]−, one can conclude that these characteristics were very similar. In view of this circumstance, it is reasonable to expect that the process of formation of the trisubstituted derivative [2,4,6-B10H7O2CCH3(NCCH3)]0 will proceed as smoothly as the process of obtaining monosubstituted derivatives [2-B10H9NCCH3]− [25].
Thus, based on theoretical calculations, it is easy to suggest a proposed experimental approach to obtain the target trisubstituted derivative [B10H7O2CCH3(NCCH3)]0 (Figure 8). The protonated form of the carboxonium derivative [2,6-B10H8O2CCH3*Hfac]0 can easily be obtained in situ through the interaction of [2,6-B10H8O2CCH3]− with excess of trifluoromethanesulfonic acid CF3SO3H [35]. Then, as follows from the presented theoretical calculations, interactions between [2,6-B10H8O2CCH3*Hfac]0 and an acetonitrile molecule CH3CN (in dichloromethane solution or in pure CH3CN) will lead to the formation of the trisubstituted derivative [2,4,6-B10H7O2CCH3(NCCH3)]0. Heating the resulting solution to its boiling point will significantly reduce the total synthesis time.

3. Materials and Methods

The DFT calculations were performed using the ORCA 4.2.1 program package [37]. The geometries of all model structures were fully optimised using the ωB97X-D3 functional in combination with the def2-TZVPP basis sets [38,39,40,41]. This method is applicable for a wide range of quantum chemical issues: atomic charges and chemical reactivity of organic and inorganic systems [42,43,44,45,46,47]. Previously, we have successfully applied the ωB97X-D3 functional for various calculations of closo-borate peculiarities: B-X (X = C, O, N, F) chemical bonding, non-covalent interactions, and molecular reactivity [35,48]. All calculations were performed using the RIJCOSX approximation with the def2/J auxiliary basis set [49]. Tight criteria of SCF convergence (“Tight SCF”) were employed for the calculations. The keywords “Grid5”, “FinalGrid6” and “GridX5” were used as parameters for the spatial integration grid. For more accurate estimation of thermodynamic characteristics, single point calculations at the DLPNO-CCSDT/cc-pvdz level were performed [50]. DLPNO-CCSDT calculations were carried out using the RIJK approximation with the cc-pvdz/c cc-pvtz/jk auxiliary basis sets. Very tight criteria of SCF convergence (“Verytight SCF”) were employed for the calculations. Zero-point corrections taken from the ωB97X-D3/def2-TZVPP computations were then added to the final energies. All considered closo-decaborate species had closed electron shells and the spin-restricted approximation was applied. During the geometry optimisation procedure, symmetry operations were not applied for the considered structures. Hessian matrices were calculated numerically for all model structures, to prove the location of correct minima on potential energy surfaces (no imaginary frequencies were found in any of the cases). The connectivity of each reaction step was also confirmed using the intrinsic reaction coordinate (IRC) calculations from the transition states [51,52,53]. Solvent molecules were not explicitly taken into account. Thus, solvent effects were considered using the Solvation Model based on Density (SMD) [54]. All calculations (geometry optimization, frequency calculation, DLPNO-CCSDT single point calculation, QTAIM analysis) were performed in a dichlromethane (CH2Cl2) phase. Topological analysis of the electron density distribution, based on the Quantum Theory of Atoms in Molecules (QTAIM) formalism developed by Bader [55,56,57], was employed with the Multiwfn program (version 3.7) [58]. The natural bond orbital (NBO) method was employed, using the NBO7 program package [59,60]. The Cartesian atomic coordinates for all optimised equilibrium model structures are presented in the Supplementary Materials. The visualisation of optimised structures was carried out with the help of the ChemCraft program (version 1.7) [61].

4. Conclusions

A comprehensive theoretical study of the mechanism for the formation of the trisubstituted derivative [B10H7O2CCH3(NCCH3)]0 was carried out. As in case of the mononitrlium derivative of closo-decaborate anion [B10H9NCCH3]−, the process of [B10H7O2CCH3(NCCH3)]0 preparation had an EINS mechanism. A trisubstituted compound was obtained on the basis of interaction of the protonated carboxonium derivative [B10H8O2CCH3(Hfac)]0 with an acetonitrile molecule CH3CN. The target trisubstituted derivative [B10H7O2CCH3(NCCH3)]0 had several possible isomers. The main pathways for the formation of such isomers were considered. The most energetically favourable pathway was the substitution of the hydrogen atom at the boron atom in the B4 position. This route had the lowest energies of the [B10H7O2CCH3(H2)]− intermediate and transition state at the elimination stage. Thus, the current theoretical study showed the possibility of obtaining a trisubstituted derivative based on a carboxonium derivative of closo-borate anions. This can be applied for developing a synthesis strategy for the preparation of such derivatives.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics11050201/s1, Table S1: Relative electronic energies (DLPNO-CCSDT/cc-pvdz level of theory) of main molecular species in kJ/mol; Table S2: Main topological parameters of electron density for interactions in B-H2 fragments. ρ(r)—electron density at the bcp, ∇2ρ(r)—Laplacian of electron density at the bcp, G Hb—total energy at the bcp, δ—delocalization index; Figure S1: Expanded general scheme for the formation of trisubstituted derivative Tris_B4; Figure S2: General scheme for the formation of trisubstituted derivative Tris_B1; Figure S3: General scheme for the formation of trisubstituted derivative Tris_B3; Figure S4: General scheme of formation of [2-B10H9NCCH3]−; Figure S5: General scheme of formation of [1-B10H9NCCH3]−; Table S3: Cartesian atomic coordinates of the calculated optimised equilibrium model structures. Gibbs energy (wB97X-D3 level; kJ/mol), electronic energy (DLPNO-CCSDT level; kJ/mol), electronic energy + ZPE corrections (DLPNO-CCSDT level; kJ/mol). All coordinates are given in Angstrom units, Å.

Author Contributions

Investigation, I.N.K., A.S.N. and A.V.K.; writing—original draft preparation, I.N.K.; writing—Review and Editing, A.S.N.; conceptualisation, A.S.N. and I.N.K.; data analysis, I.N.K., A.S.N. and A.V.K.; bond order analysis, A.S.N.; supplementary material preparation, A.V.K. and A.P.Z.; visualisation, A.P.Z. and I.N.K.; editing, data analysis and interpretation, A.S.N., I.N.K. and A.P.Z.; supervision, K.Y.Z. and N.T.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Russian Science Foundation (project No. 22-73-00201).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This work was prepared in commemoration of the 300th anniversary of St Petersburg State University’s founding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hagemann, H. Boron hydrogen compounds: Hydrogen storage and battery applications. Molecules 2021, 26, 7425. [Google Scholar] [CrossRef] [PubMed]
  2. Fink, K.; Uchman, M. Boron cluster compounds as new chemical leads for antimicrobial therapy. Coord. Chem. Rev. 2021, 431, 213684. [Google Scholar] [CrossRef]
  3. Zhao, X.; Yang, Z.; Chen, H.; Wang, Z.; Zhou, X.; Zhang, H. Progress in three-dimensional aromatic-like closo-dodecaborate. Coord. Chem. Rev. 2021, 444, 214042. [Google Scholar] [CrossRef]
  4. Gigante, A.; Duchêne, L.; Moury, R.; Pupier, M.; Remhof, A.; Hagemann, H. Direct Solution-Based Synthesis of Na4(B12H12)(B10H10) Solid Electrolyte. ChemSusChem 2019, 12, 4832–4837. [Google Scholar] [CrossRef] [PubMed]
  5. Duchêne, L.; Lunghammer, S.; Burankova, T.; Liao, W.-C.; Embs, J.P.; Copéret, C.; Wilkening, H.M.R.; Remhof, A.; Hagemann, H.; Battaglia, C. Ionic Conduction Mechanism in the Na2(B12H12)0.5(B10H10)0.5 Closo-Borate Solid-State Electrolyte: Interplay of Disorder and Ion–Ion Interactions. Chem. Mater. 2019, 31, 3449–3460. [Google Scholar] [CrossRef]
  6. Laskova, J.; Serdyukov, A.; Kosenko, I.; Ananyev, I.; Titova, E.; Druzina, A.; Sivaev, I.; Antonets, A.A.; Nazarov, A.A.; Bregadze, V.I. New Azido Coumarins as Potential Agents for Fluorescent Labeling and Their “Click” Chemistry Reactions for the Conjugation with closo-Dodecaborate Anion. Molecules 2022, 27, 8575. [Google Scholar] [CrossRef] [PubMed]
  7. Diab, M.; Mateo, A.; El Cheikh, J.; El Hajj, Z.; Haouas, M.; Ranjbari, A.; Guérineau, V.; Touboul, D.; Leclerc, N.; Cadot, E.; et al. Grafting of Anionic Decahydro-Closo-Decaborate Clusters on Keggin and Dawson-Type Polyoxometalates: Syntheses, Studies in Solution, DFT Calculations and Electrochemical Properties. Molecules 2022, 27, 7663. [Google Scholar] [CrossRef]
  8. Dou, D.; Mavunkal, I.J.; Bauer, J.A.K.; Knobler, C.B.; Hawthorne, M.F.; Shore, S.G. Synthesis and Structure of Triethylammonium 2-(Acetonitrile)nonahydro-closo-decaborate(1-). Inorg. Chem. 1994, 33, 6432–6434. [Google Scholar] [CrossRef]
  9. Bayer, M.J.; Hawthorne, M.F. An Improved Method for the Synthesis of [closo-B12(OH)12]−2. Inorg. Chem. 2004, 43, 2018–2020. [Google Scholar] [CrossRef]
  10. Al-Joumhawy, M.; Cendoya, P.; Shmalko, A.; Marei, T.; Gabel, D. Improved synthesis of halo- and oxonium derivatives of dodecahydrido-closo-dodecaborate(2-). J. Organomet. Chem. 2021, 949, 121967. [Google Scholar] [CrossRef]
  11. Semioshkin, A.A.; Sivaev, I.B.; Bregadze, V.I. Cyclic oxonium derivatives of polyhedral boron hydrides and their synthetic applications. Dalton Trans. 2008, 11, 977–992. [Google Scholar] [CrossRef] [PubMed]
  12. Zhu, T.-C.; Xing, Y.-Y.; Sun, Y.; Duttwyler, S.; Hong, X. Directed B–H functionalization of the closo -dodecaborate cluster via concerted iodination–deprotonation: Reaction mechanism and origins of regioselectivity. Org. Chem. Front. 2020, 7, 3648–3655. [Google Scholar] [CrossRef]
  13. Sun, Y.; Zhang, J.; Zhang, Y.; Liu, J.; van der Veen, S.; Duttwyler, S. The closo -Dodecaborate Dianion Fused with Oxazoles Provides 3D Diboraheterocycles with Selective Antimicrobial Activity. Chem.-A Eur. J. 2018, 24, 10364–10371. [Google Scholar] [CrossRef] [PubMed]
  14. Cao, K.; Zhang, C.-Y.; Xu, T.-T.; Wu, J.; Wen, X.-Y.; Jiang, W.-J.; Chen, M.; Yang, J. Synthesis of Polyhedral Borane Cluster Fused Heterocycles via Transition Metal Catalyzed B-H Activation. Molecules 2020, 25, 391. [Google Scholar] [CrossRef] [PubMed]
  15. Shelly, K.; Knobler, C.B.; Hawthorne, F. Synthesis of Monosubstituted Derivatives of closo -Decahydrodecaborate(2-). X-ray Crystal Structures of [closo-2-B10H9CO]− and [closo-2- B10H9NCO]−. Inorg. Chem. 1992, 31, 2889–2892. [Google Scholar] [CrossRef]
  16. Laskova, J.; Ananiev, I.; Kosenko, I.; Serdyukov, A.; Stogniy, M.; Sivaev, I.; Grin, M.; Semioshkin, A.; Bregadze, V.I. Nucleophilic addition reactions to nitrilium derivatives [B12H11NCCH3]− and [B12H11NCCH2CH3]−. Synthesis and structures of closo -dodecaborate-based iminols, amides and amidines. Dalton Trans. 2022, 51, 3051–3059. [Google Scholar] [CrossRef]
  17. Kaszyński, P.; Ringstrand, B. Functionalization of closo-borates via iodonium zwitterions. Angew. Chem.-Int. Ed. 2015, 54, 6576–6581. [Google Scholar] [CrossRef]
  18. Laila, Z.; Yazbeck, O.; Ghaida, F.A.; Diab, M.; El Anwar, S.; Srour, M.; Mehdi, A.; Naoufal, D. Clean-activation of the B–H bond in closo-decahydrodecaborate [B10H10]2− anion via soft-route. J. Organomet. Chem. 2020, 910, 121132. [Google Scholar] [CrossRef]
  19. Knoth, W.H.; Sauer, J.C.; England, D.C.; Hertler, W.R.; Muetterties, E.L. Chemistry of Boranes. XIX. 1 Derivative Chemistry of B10H10−2 and B12H12−2. J. Am. Chem. Soc. 1964, 86, 3973–3983. [Google Scholar] [CrossRef]
  20. Miller, H.C.; Miller, N.E.; Muetterties, E.L. Chemistry of Boranes. XX. Syntheses of Polyhedral Boranes. Inorg. Chem. 1964, 3, 1456–1463. [Google Scholar] [CrossRef]
  21. Jelinek, T.; Štibr, B.; Mareš, F.; Plešek, J.; Heřmánek, S. Halogenation of 4,5-dicarba-arachno- nonaborane(13),4,5-C2B7H13. Polyhedron 1987, 6, 1737–1740. [Google Scholar] [CrossRef]
  22. Frank, R.; Adhikari, A.K.; Auer, H.; Hey-Hawkins, E. Electrophile-induced nucleophilic substitution of the nido- dicarbaundecaborate anion nido-7,8-C2B9H12 by conjugated heterodienes. Chem.-A Eur. J. 2014, 20, 1440–1446. [Google Scholar] [CrossRef] [PubMed]
  23. Mahfouz, N.; Ghaida, F.A.; El Hajj, Z.; Diab, M.; Floquet, S.; Mehdi, A.; Naoufal, D. Recent Achievements on Functionalization within closo-Decahydrodecaborate [B10H10]2− Clusters. ChemistrySelect 2022, 7, e202200770. [Google Scholar] [CrossRef]
  24. Sivaev, I.B.; Kulikova, N.Y.; Nizhnik, E.A.; Vichuzhanin, M.V.; Starikova, Z.A.; Semioshkin, A.A.; Bregadze, V.I. Practical synthesis of 1,4-dioxane derivative of the closo-dodecaborate anion and its ring opening with acetylenic alkoxides. J. Organomet. Chem. 2008, 693, 519–525. [Google Scholar] [CrossRef]
  25. Stogniy, M.Y.; Erokhina, S.A.; Sivaev, I.B.; Bregadze, V.I. Nitrilium derivatives of polyhedral boron compounds (boranes, carboranes, metallocarboranes): Synthesis and reactivity. Phosphorus Sulfur Silicon Relat. Elem. 2019, 194, 983–988. [Google Scholar] [CrossRef]
  26. Sivaev, I.B.; Prikaznov, A.V.; Naoufal, D. Fifty years of the closo-decaborate anion chemistry. Collect. Czechoslov. Chem. Commun. 2010, 75, 1149–1199. [Google Scholar] [CrossRef]
  27. Sivaev, I.B.; Bregadze, V.I.; Sjöberg, S. Chemistry of closo-Dodecaborate Anion [B12H12]2−: A Review. Collect. Czechoslov. Chem. Commun. 2002, 67, 679–727. [Google Scholar] [CrossRef]
  28. Golub, I.E.; Filippov, O.A.; Belkova, N.V.; Epstein, L.M.; Shubina, E.S. The Mechanism of Halogenation of Decahydro-closo-Decaborate Dianion by Hydrogen Chloride. Russ. J. Inorg. Chem. 2021, 66, 1639–1648. [Google Scholar] [CrossRef]
  29. Golub, I.E.; Filippov, O.A.; Belkova, N.V.; Epstein, L.M.; Shubina, E.S. The reaction of hydrogen halides with tetrahydroborate anion and hexahydro-closo-hexaborate dianion. Molecules 2021, 26, 3754. [Google Scholar] [CrossRef]
  30. Kochnev, V.K.; Avdeeva, V.V.; Malinina, E.A.; Kuznetsov, N.T. Theoretical study of H2 Elimination from [BnHn+1] monoanions (n = 6–9, 11). Russ. J. Inorg. Chem. 2014, 59, 1268–1275. [Google Scholar] [CrossRef]
  31. Klyukin, I.N.; Kubasov, A.S.; Limarev, I.P.; Zhdanov, A.P.; Matveev, E.Y.; Polyakova, I.N.; Zhizhin, K.Y.; Kuznetsov, N.T. The new approach to formation of exo boron-oxygen bonds from the decahydro-closo-decaborate(2-) anion. Polyhedron 2015, 101, 215–222. [Google Scholar] [CrossRef]
  32. Ezhov, A.V.; Vyal’ba, F.Y.; Kluykin, I.N.; Zhdanova, K.A.; Bragina, N.A.; Zhdanov, A.P.; Zhizhin, K.Y.; Mironov, A.F.; Kuznetsov, N.T. Synthesis of New Bioinorganic Systems Based on Nitrilium Derivatives of closo-Decaborate Anion and meso-Arylporphyrins with Pendant Amino Groups. Macroheterocycles 2017, 10, 505–509. [Google Scholar] [CrossRef]
  33. Klyukin, I.N.; Zhdanov, A.P.; Matveev, E.Y.; Razgonyaeva, G.A.; Grigoriev, M.S.; Zhizhin, K.Y.; Kuznetsov, N.T. Synthesis and reactivity of closo-decaborate anion derivatives with multiple carbon-oxygen bonds. Inorg. Chem. Commun. 2014, 50, 28–30. [Google Scholar] [CrossRef]
  34. Klyukin, I.N.; Kolbunova, A.V.; Novikov, A.S.; Nelyubin, A.V.; Zhdanov, A.P.; Kubasov, A.S.; Selivanov, N.A.; Bykov, A.Y.; Zhizhin, K.Y.; Kuznetsov, N.T. Synthesis of Disubstituted Carboxonium Derivatives of Closo-Decaborate Anion [2,6-B10H8O2CC6H5]−: Theoretical and Experimental Study. Molecules 2023, 28, 1757. [Google Scholar] [CrossRef]
  35. Klyukin, I.N.; Kolbunova, A.V.; Novikov, A.S.; Nelyubin, A.V.; Selivanov, N.A.; Bykov, A.Y.; Klyukina, A.A.; Zhdanov, A.P.; Zhizhin, K.Y.; Kuznetsov, N.T. Protonation of Borylated Carboxonium Derivative [2,6-B10H8O2CCH3]−: Theoretical and Experimental Investigation. Int. J. Mol. Sci. 2022, 23, 4190. [Google Scholar] [CrossRef]
  36. Kochnev, V.K.; Kuznetsov, N.T. Theoretical study of protonation of the B10H102− anion and subsequent hydrogen removal due to substitution reaction in acidic medium. Comput. Theor. Chem. 2016, 1075, 77–81. [Google Scholar] [CrossRef]
  37. Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73. [Google Scholar] [CrossRef]
  38. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  39. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787. [Google Scholar] [CrossRef]
  40. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456. [Google Scholar] [CrossRef]
  41. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracyElectronic supplementary information. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  42. Nikolova, V.; Cheshmedzhieva, D.; Ilieva, S.; Galabov, B. Atomic Charges in Describing Properties of Aromatic Molecules. J. Org. Chem. 2019, 84, 1908–1915. [Google Scholar] [CrossRef]
  43. Oller, J.; Pérez, P.; Ayers, P.W.; Vöhringer-Martinez, E. Global and local reactivity descriptors based on quadratic and linear energy models for α, β -unsaturated organic compounds. Int. J. Quantum Chem. 2018, 118, e25706. [Google Scholar] [CrossRef]
  44. Cheriet, M.; Madi, F.; Nouar, L.; Lafifi, I.; Himri, S.; Merabet, N.; Khatmi, D. A DFT study of inclusion complexes of the antituberculosis drugs pyrazinamide and isoniazid with cucurbit[7]uril. J. Incl. Phenom. Macrocycl. Chem. 2017, 89, 127–136. [Google Scholar] [CrossRef]
  45. Kee, C.W. Molecular Understanding and Practical In Silico Catalyst Design in Computational Organocatalysis and Phase Transfer Catalysis—Challenges and Opportunities. Molecules 2023, 28, 1715. [Google Scholar] [CrossRef] [PubMed]
  46. Basdogan, Y.; Groenenboom, M.C.; Henderson, E.; De, S.; Rempe, S.B.; Keith, J.A. Machine Learning-Guided Approach for Studying Solvation Environments. J. Chem. Theory Comput. 2020, 16, 633–642. [Google Scholar] [CrossRef]
  47. Xavier, N.F.; Da Silva, A.M.; Bauerfeldt, G.F. Supercell calculations of the geometry and lattice energy of α-glycine crystal. J. Mol. Model. 2019, 25, 244. [Google Scholar] [CrossRef]
  48. Neumolotov, N.K.; Selivanov, N.A.; Bykov, A.Y.; Klyukin, I.N.; Novikov, A.S.; Zhdanov, A.P.; Zhizin, K.Y.; Kuznetsov, N.T. New Methods for Preparation of the Monofluorosubstituted Derivative of the closo-Borate Anion [2-B10H9F]2−, Its Properties, and Analysis of Its Reactivity. Russ. J. Inorg. Chem. 2022, 67, 1583–1590. [Google Scholar] [CrossRef]
  49. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  50. Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
  51. Gonzalez, C.; Schlegel, H.B. Improved algorithms for reaction path following: Higher-order implicit algorithms. J. Chem. Phys. 1991, 95, 5853–5860. [Google Scholar] [CrossRef]
  52. Gonzalez, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
  53. Gonzalez, C.; Schlegel, H.B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. [Google Scholar] [CrossRef]
  54. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
  55. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  56. Bader, R.; Legare, D. Properties of atoms in molecules: Structures and reactivities of boranes and carboranes. Can. J. Chem. 1992, 70, 657–677. [Google Scholar] [CrossRef]
  57. Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
  58. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comp. Chem. 2011, 33, 580–592. [Google Scholar] [CrossRef]
  59. Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 9781118229101. [Google Scholar]
  60. Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New vistas in localized and delocalized chemical bonding theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef]
  61. Chemcraft—Graphical Software for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com (accessed on 27 April 2023).
Inorganics 11 00201 g001 550
Figure 1. (a) Optimised structure of [B10H8O2CCH3(Hfac)]0. (b) Atomic number order in [B10H8O2CCH3(Hfac)]0. Exo-polyhedral atoms of hydrogen were omitted for clarity. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Figure 1. (a) Optimised structure of [B10H8O2CCH3(Hfac)]0. (b) Atomic number order in [B10H8O2CCH3(Hfac)]0. Exo-polyhedral atoms of hydrogen were omitted for clarity. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Inorganics 11 00201 g001
Inorganics 11 00201 g002 550
Figure 2. Optimised structures of hydrogen migration transition states TSmigr_B1, TSmigr_B3 and TSmigr_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Figure 2. Optimised structures of hydrogen migration transition states TSmigr_B1, TSmigr_B3 and TSmigr_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Inorganics 11 00201 g002
Inorganics 11 00201 g003 550
Figure 3. Optimised structures of H2_B1, H2_B3 and H2_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å. Interactions between boron atoms and Hfac are marked with orange dotted lines. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Figure 3. Optimised structures of H2_B1, H2_B3 and H2_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å. Interactions between boron atoms and Hfac are marked with orange dotted lines. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Inorganics 11 00201 g003
Inorganics 11 00201 g004 550
Figure 4. Molecular graph showing the results of the topological analysis of the electron density distribution in the model structure of H2_B1, H2_B3 and H2_B4.
Figure 4. Molecular graph showing the results of the topological analysis of the electron density distribution in the model structure of H2_B1, H2_B3 and H2_B4.
Inorganics 11 00201 g004
Inorganics 11 00201 g005 550
Figure 5. Optimised structures of hydrogen elimination transition states TSelim_B1, TSelim_B3 and TSelim_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Figure 5. Optimised structures of hydrogen elimination transition states TSelim_B1, TSelim_B3 and TSelim_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å. Interactions between boron atoms and Hfac are marked with orange dotted lines.
Inorganics 11 00201 g005
Inorganics 11 00201 g006 550
Figure 6. Optimised structures of target trisubstituted derivatives Tris_B1, Tris_B3 and Tris_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å.
Figure 6. Optimised structures of target trisubstituted derivatives Tris_B1, Tris_B3 and Tris_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red. Bond lengths are given in Angstroms, Å.
Inorganics 11 00201 g006
Inorganics 11 00201 g007 550
Figure 7. General scheme for the formation of trisubstituted derivative Tris_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red.
Figure 7. General scheme for the formation of trisubstituted derivative Tris_B4. Relative Gibbs energy (wB97X-D3 level; kJ/mol) is marked in black and relative electronic energy (DLPNO-CCSDT level + ZPE corrections; kJ/mol) is marked in red.
Inorganics 11 00201 g007
Inorganics 11 00201 g008 550
Figure 8. Proposed scheme of experimental formation of [2,4,6-B10H7O2CCH3(NCCH3)]0.
Figure 8. Proposed scheme of experimental formation of [2,4,6-B10H7O2CCH3(NCCH3)]0.
Inorganics 11 00201 g008
Table
Table 1. DFT (wB97X-D3/def2-TZVPP level of theory) relative Gibbs free energies of main molecular species and relative electronic energies with ZPE (DLPNO-CCSDT/cc-pvdz + ZPE level of theory) in kJ/mol.
Table 1. DFT (wB97X-D3/def2-TZVPP level of theory) relative Gibbs free energies of main molecular species and relative electronic energies with ZPE (DLPNO-CCSDT/cc-pvdz + ZPE level of theory) in kJ/mol.
Model SpeciesDFTDLPNO-CCSDT
[B10H8O2CCH3(Hfac)] + CH3CN0.00.0
Formation of Tris_B1
TSmigr_B1 + CH3CN46.653.7
H2_B1 + CH3CN43.152.3
TSelim_B1195.9157.8
Tris_B1 + H2−81.1−97.6
Formation of Tris_B3
Tsmigr_B3 + CH3CN38.648.2
H2_B3 + CH3CN27.639.7
Tselim_B3151.0115.1
Tris_B3 + H2−83.4−100.9
Formation of Tris_B4
TSmigr_B4 + CH3CN33.143.6
H2_B4 + CH3CN19.932.5
TSelim_B4145.2109.5
Tris_B4 + H2−88.5−106.5
[B10H11]− + CH3CN0.00.0
Formation of [1-B10H9NCCH3]−
B10_TSmigr_ap + CH3CN49.157.2
B10_H2_ap + CH3CN41.552.0
B10_TSelim_ap195.7159.1
[1-B10H9NCCH3]− + H2−57.9−74.5
Formation of [2-B10H9NCCH3]−
B10_TSmigr_eq + CH3CN59.168.2
B10_H2_eq + CH3CN29.842.2
B10_TSelim_eq139.9104.2
[2-B10H9NCCH3]− +H2−58.9−75.9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Klyukin, I.N.; Kolbunova, A.V.; Novikov, A.S.; Zhdanov, A.P.; Zhizhin, K.Y.; Kuznetsov, N.T. Theoretical Insight on the Formation Mechanism of a Trisubstituted Derivative of Closo-Decaborate Anion [B10H7O2CCH3(NCCH3)]0. Inorganics 2023, 11, 201. https://doi.org/10.3390/inorganics11050201

AMA Style

Klyukin IN, Kolbunova AV, Novikov AS, Zhdanov AP, Zhizhin KY, Kuznetsov NT. Theoretical Insight on the Formation Mechanism of a Trisubstituted Derivative of Closo-Decaborate Anion [B10H7O2CCH3(NCCH3)]0. Inorganics. 2023; 11(5):201. https://doi.org/10.3390/inorganics11050201

Chicago/Turabian Style

Klyukin, Ilya N., Anastasia V. Kolbunova, Alexander S. Novikov, Andrey P. Zhdanov, Konstantin Yu. Zhizhin, and Nikolay T. Kuznetsov. 2023. "Theoretical Insight on the Formation Mechanism of a Trisubstituted Derivative of Closo-Decaborate Anion [B10H7O2CCH3(NCCH3)]0" Inorganics 11, no. 5: 201. https://doi.org/10.3390/inorganics11050201

APA Style

Klyukin, I. N., Kolbunova, A. V., Novikov, A. S., Zhdanov, A. P., Zhizhin, K. Y., & Kuznetsov, N. T. (2023). Theoretical Insight on the Formation Mechanism of a Trisubstituted Derivative of Closo-Decaborate Anion [B10H7O2CCH3(NCCH3)]0. Inorganics, 11(5), 201. https://doi.org/10.3390/inorganics11050201

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop