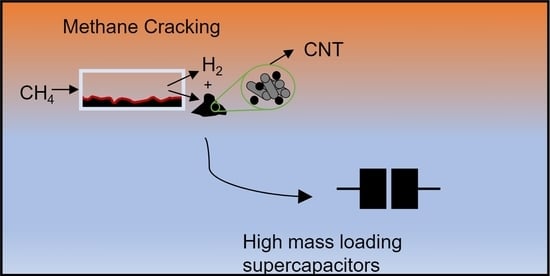
Superior Rate Capability of High Mass Loading Supercapacitors Fabricated with Carbon Recovered from Methane Cracking

Abstract

High mass loading (ca. 30 mg/cm²) electrodes were prepared with carbon recovered from catalytic methane cracking (MC). As-fabricated supercapacitors displayed 74% of capacitance retention from 6 mA/cm² to 60 mA/cm² and a Ragone plot’s slope of −7 Wh/kW (compared to 42% and −31 Wh/kW, respectively, for high mass loading devices fabricated with commercial carbon). The high-rate capability of the MC-recovered carbon is attributed to the presence of carbon black and carbon nanotubes produced during the reaction, which likely increased the electronic and ionic conductivity within the electrode. These results suggest that the by-product of this hydrogen generation route might be a suitable active material for supercapacitors.

1. Introduction

To avoid unreversible climate change, the IPCC has recently stressed the need to urgently decarbonize our society [1]. This has renewed the interest in hydrogen as a clean energy vector [2]. However, ca. 97% of the hydrogen is currently obtained via steam methane reforming, which is a CO₂-emitting process [3]. Catalytic methane cracking (or “methane pyrolysis”) does not present this problem since, in the absence of oxygen, the only by-product is solid carbon [4]. However, for this particular H₂ generation route to become a bridge to the hydrogen economy [5], it is important to find a suitable application for the large amounts of solid carbon that will be generated as a by-product upon this technology’s upscaling. If all the hydrogen generated in the world in 2020 (ca. 90 Mt) had been obtained via methane cracking, ca. 45 Mt of solid carbon would have been produced (and, to meet the goal of net zero emissions by 2050, this figure should double until 2030) [6].

Supercapacitors, an energy storage technology with a growing demand for high-power applications, could be an interesting route for draining this by-product, since carbon is the main component of their electrodes [7]. The features of the carbon obtained upon catalytic methane cracking depend on the reaction parameters (e.g., temperature) and on the nature of the catalyst (which is used in order to bring down the reaction temperature) [8,9]. Carbon-based catalysts appear to favor the formation of carbon black, whilst metal oxide-based catalysts have been shown to generate carbon nanotubes (CNT) more often [10]. Either way, both carbon black and CNTs are useful additives for carbon-based supercapacitor electrodes: both enhance electrical conductivity [11], and the latter also facilitates ionic transport within the electrodes [12].

These improvements are particularly relevant for thick electrodes, where the increased impedance usually precludes an effective utilization of all the theoretically active mass, especially when working at high current densities [13] (Figure 1).

As a result, the specific capacitance of the as-fabricated cells is smaller and, at high rates, their energy density is low because of the large fraction of “dead weight” [14]. Due to these problems, most widely published studies resort to electrodes with very low mass loadings (<5 mg/cm²) and reach artificially high performances, which do not reflect the behavior that the material would display in a commercial device [15]. Industries typically use high mass loading electrodes (ca. 10 mg/cm²) since, unlike the literature-reported results, the gravimetric performance of commercial supercapacitors is evaluated for the whole device (i.e., including the masses of the current collector, separator, casing, etc.) [16], and thus, if the active material’s mass were too low (compared to the overall mass), the gravimetric performance would be unacceptable. In a nutshell, low mass loadings lead to low energy and power densities in commercial devices, but high mass loadings do not allow for high energy densities at high power densities. Using the nanocarbons-enriched by-product of methane cracking (MC) in thick supercapacitor electrodes could increase their ionic and electronic conductivities and thus circumvent this impasse.

Some authors have already explored the capabilities of the carbon derived from a methane-to-hydrogen conversion process as an active material for supercapacitor electrodes. Zhang et al. [17] employed a charcoal-supported K₂CO₃ catalyst to obtain syngas (H₂ and CO) by methane dry reforming (MDR) and used the waste carbon as a supercapacitor material. The device, which worked with a KOH electrolyte, achieved a remarkable specific capacitance of 133 F/g @ 1 A/g, attributed to the carbon fibers formed upon the conversion process. Similarly, Krishnamoorthy et al. [18] fabricated supercapacitors from the spent catalyst of MDR, and the symmetric device (carbon-coated siloxane/Ni foam electrodes in 1M of TEABF₄) demonstrated a good rate capability but also a lower specific capacitance (ca. 25 F/g). Notwithstanding, in both cases, although the hydrogen generation did not release any greenhouse gases, it emitted CO, which is highly toxic [19]. Moreover, the supercapacitors fabricated with the reactions’ waste carbon had low mass loadings, and thus, their performances are hardly comparable to those of commercial devices.

Herein, we report that ultra-high mass loading supercapacitors (ca. 30 mg/cm²) fabricated with MC-recovered carbon from a clean and non-toxic H₂ generation route achieved, at high current densities, a higher performance than analogous devices prepared with commercial carbon.

2. Results and Discussion

Figure 2 shows a micrograph, taken at a ×10,000 magnification, for the carbon collected after the MC, where long filaments corresponding to carbon nanotubes wrapped around smaller particles (possibly carbon black) are visible.

Figure 3 shows, both for commercial carbon and for MC-recovered carbon, voltammograms obtained at increasing scan rates (Figure 3a,b, respectively) and galvanostatic charge–discharge curves obtained at increasing current densities (Figure 3c,d, respectively). At low rates, the voltammograms of commercial carbon (Figure 3a) are fairly rectangular and have a larger area; however, as the scan rate increases, their shape approaches that of an elongated ellipse (suggesting a high resistivity). Similarly, the charge–discharge curves show that whilst, at low current densities, commercial carbon cells have a longer (dis)charge period (which indicates a higher capacitance), their performance decreases rapidly with increasing current densities (resulting in large ohmic drops). On the contrary, the cells prepared with MC-recovered carbon manage to retain highly rectangular voltammograms (even at 100 mV/s), and their charge–discharge plots have consistently lower ohmic drops.

Figure 4 shows almost the same information represented in Figure 3, but enhancing the results obtained exclusively at very high rates (which are the ones that matter the most in this context). Comparing the two plots in Figure 4a, it becomes clear that only the cells fabricated with the MC-recovered carbon manage to retain a good capacitive behavior at high scan rates (100 mV/s). This is also demonstrated in Figure 4b, where the “fill factors” represent how close the voltammograms are to an ideal rectangle.

These results suggest an enhanced electric and ionic conductivity, also supported by the lower ohmic drop at extremely high current densities (Figure 4c,d). However, it is still quite high. This can be attributed to the ultra-high mass loadings (most literature-reported supercapacitor electrodes have mass loadings of <2 mg/cm² [20], whilst these have 30 mg/cm²) combined with the usage of an ultra-high current density. It is worth noting that supercapacitors are usually not tested above 50 mA/cm² (when high gravimetric current densities are reported, these are often due to very low mass loadings).

Figure 5 shows impedance measurements and respective fittings.

As shown in Figure 5, the data are well fitted to the equivalent electric circuit shown in the inset (similar to those used by Köps et al. [21] and Dsoke et al. [22]). Circuit fitting is not a straightforward task, and it often requires a trial-and-error approach. An equivalent electric circuit should be sophisticated enough to simulate the real behavior of the system as accurately as possible but also simple enough to remain intelligible and to enable the attribution of some physical meaning to its components.

The physical meaning of an impedance measurement is deeply tied to the frequency at which it was collected. Since each frequency is associated with a certain rate of charge/discharge, which, in turn, enables a certain level of ionic penetration within the electrode, the set of generated impedances provides information about different parts of the electrode|electrolyte system.

At ultrahigh frequencies (>50 kHz), the supercapacitor behaves basically as a resistor (R₁). This resistance (often called “series resistance”, since it is mostly the result of extrinsic contributions) includes not only the wiring and ohmic junctions (e.g., the contact resistance between the crocodile clips and the cell’s terminals) but also the resistivity of the bulk electrolyte [21]. At lower—but still high—frequencies (between 100 Hz and 50 kHz), the Nyquist plot of the device shows approximately a semi-circle.

This behavior is usually modeled by a capacitor in parallel with a resistor (R₂) [23]. Since, at these high frequencies, the ions are still not allowed enough time to diffuse deep within the electrode, only the outmost pores (directly in contact with the electrolyte) contribute to capacitance, and thus, the obtained values are typically a few orders of magnitude below the nominal capacitance. Under these conditions, the formation of the double-layer is mostly limited by the mobility of the electrons within the electrode. R₂ is thus mainly influenced by the thickness of the electrode and by its overall resistivity, which, in turn, is affected by the conductivities of the carbon particles and by the contact resistances between adjacent grains and between these and the current collector [22]. CNTs (and carbon black as well) are significantly more conducting than activated carbon, and thus, their presence in the MC-recovered carbon likely explains the large reduction in R₂ (0.6 Ω vs. 3.4 Ω, as displayed in

Table 1. Fitting parameters obtained for the equivalent electric circuits of the cells prepared with MC-recovered carbon and with commercial carbon.

	MC-Recovered	Commercial ca
R1 (Ω)	1.8	1.5
R2 (Ω)	0.6	3.4
CPE (sN/Ω)	8.0 × 10−5	2.1 × 10−5
N	0.9	0.9
W ($\sqrt{s}$/ Ω)	0.36	0.29
R3 (Ω)	1.9	2.1
C (F)	1.1	1.6

).

As for the “capacitor” in parallel with R₂, given the imperfect nature of the double-layer, it is actually more accurately modeled by a constant phase element (CPE). This circuit component has two features: its magnitude and its dispersion coefficient (N). The latter varies between 0 and 1: for N = 0, the element behaves like a perfect resistor, whilst, for N = 1, it behaves like a perfect capacitor [24]. In this case, N is quite high (N = 0.9), meaning that the magnitude of the CPE (in this case, represented as an admittance) can be roughly correlated with a capacitance. Because the magnitude of the CPE is larger for the MC-recovered carbon than for the commercial carbon, this suggests that the former has a higher capacitance at high frequencies (which further confirms the higher rate capability of this material).

At intermediate frequencies (typically between 100 Hz and 100 mHz), there is a transition regime which is diffusion-controlled. This behavior is often modeled by a Warburg element (W). However, because the Warburg element assumes that the diffusion process can be considered semi-infinite [25] (which is true for some pores but not for others), adding a resistance in parallel with this element (R₃) significantly improves the quality of the fitting by accounting for the large heterogeneity of time responses. In other words, while some ions are still freely diffusing across the electrodes, at the same time, others have already “hit pore walls” (i.e., are already in a bounded-diffusion regime, which is characteristic of the capacitive behavior). As the frequency decreases, more and more ions will have enough time to reach the diffusion boundaries and thus present a capacitive behavior (represented as a nearly vertical line in the Nyquist plot). The fact that R₃ is slightly lower for the MC-recovered carbon than for the commercial carbon suggests that the transition to the capacitive behavior is easier in the former. This enhanced transport might also be caused by CNTs acting as “ionic highways” and shortening the diffusion pathway. The maximum capacitance (obtained at ultra-low frequencies, at around 40 mHz) is, however, smaller for the MC-recovered carbon than for the commercial carbon. This is aligned with the results shown in Figure 6a.

Figure 6a shows the average areal capacitances obtained at several current densities for the symmetric coin cells fabricated with the two types of carbon.

MC-recovered carbon presents a lower areal capacitance (and a lower energy density) at low current densities, suggesting a lower SSA (confirmed by BET measurements—Figure S3). The fact that this carbon also contains CNTs (whose specific surface area is lower than that of activated carbon [26]) and some fragments of quartz wool (which were used in the inlet and outlet of the furnace and in the MC setup and unintentionally made their way into the MC-recovered carbon) probably accounts for the lower SSA.

These SiO₂ fibers (which could not be completely filtered out from the MC-recovered carbon) do not contribute to capacitance and thus only count as “dead weight”, hence bringing down the overall capacitance of the device. Nevertheless, it is worth stressing that the behavior at high current densities is the most relevant for supercapacitors since these are expected to work at high rates. Within this range (where the ions are allowed less time to reach the inner parts of the electrode), the MC-recovered carbon devices outperform the commercial carbon ones. Moreover, the MC-recovered carbon has a 74% capacitance retention from 6 mA/cm² to 60 mA/cm² (compared to only 42% for commercial carbon). In other words, for the device fabricated with commercial carbon, a significant percentage of its surface area is inaccessible to the electrolyte at high rates, and thus, its performance becomes unacceptable. MC-recovered carbon devices, however, are still performing at 167 mA/cm².

The results observed in Figure 6a are reinforced in Figure 6b, which compares the Ragone plots obtained for the two types of devices. Due to a decrease in the capacitance and to an increase in the ohmic drop, the energy and power densities of the commercial carbon device are highly degraded at high rates (the slope of the Ragone plot is −31 Wh/kW). For MC-recovered carbon, good performance is retained at high rates (the Ragone plot’s slope is only −7 Wh/kW). This metric is useful in comparing the performances of devices with similar thicknesses [27]. However, for devices with very different mass loadings (which is often the case when comparing literature-reported results), it is preferable to compare the areal capacitances at increasing current densities, as shown in Figure 7. It is worth stressing that all the areal capacitances reported were normalized by the footprint area (i.e., not by the BET surface area).

Among similar devices, MC-recovered carbon is in the top three (despite being, unlike the others, a non-optimized material that contains SiO₂ fibers). This superior rate capability at high mass loadings can probably be explained both by the additional conductive carbon black particles (resulting from MC) and by the presence of carbon nanotubes. Indeed, these appear to have a diameter of ca. 50 nm (which is ca. 50× larger than the size of the solvated ions) and thus may act as “highways”, enabling fast ionic transport into the inner parts of the electrode.

3. Materials and Methods

3.1. Methane Cracking

The MC has been performed in a fluidized bed reactor in an oxygen-free environment, at 850 °C, using an iron-based catalyst and commercial activated carbon as a support, at an inlet flow rate of 12.5 mL/min. Quartz wool was used at the inlet and outlet of the furnace. Due to the limited size of the reactor, two runs had to be performed to obtain enough carbon for the supercapacitor electrodes.

The carbon recovered from MC contained the methane-derived carbon, the carbon-supported catalyst and also some quartz wool fibers (which could not be completely filtered out). In each run, the loading of commercial carbon was ca. 4.5 g, and, since the reaction was performed for ca. 6 h, at an average conversion efficiency of 90%, the average contribution of methane-derived carbon to the total amount of carbon was estimated to be ca. 33% (i.e., approximately 2.2 g of by-product carbon would be produced per run), as detailed in ESI.

To investigate the morphology of the carbon generated upon methane cracking, the powder was placed on conductive carbon tape on top of aluminum stubs, and the electrical conductivity of the sample was further improved with a sputter-coated mixture of Au–Pd. Scanning electron micrographs (SEM) were recorded with a Field Emission Scanning Electron Microscope, JSM-7800F (by JEOL), at 5 kV in vacuum.

3.2. Electrodes and Coin Cells Preparation

Since the MC-recovered carbon contained some agglomerates, it was further ground with a mortar and pestle until roughly uniformly sized particles were observable by eye and then incorporated into a slurry with the following composition: 92.5 wt% of carbon, 5 wt% of PTFE (60 wt% dispersion in water from Sigma Aldrich, UK) and 2.5 wt% of carbon black (Super C65). The carbon, binder and conductive additive were dispersed in ethanol (20 mL per gram of dry mixture) and then further mixed for ca. 20 min, using a three-roll mill (EXAKT 50 I), at the maximum speed (500 rpm).

For comparison, a similar slurry was prepared with commercial supercapacitor-grade carbon (YP-50F, Kuraray) instead of the MC-recovered carbon. Each slurry was then rolled into a film with a ca. 600 µm thickness—this was the maximum thickness that could be achieved while preserving the mechanical integrity of the electrode without having to increase the binder content. Several identical circles with a 16 mm diameter were cut out of each film, and then the electrodes were dried overnight in an oven at 115 °C. All the electrodes were weighed, and an average mass loading of 30 ± 3.5 mg/cm² (1σ) was determined.

The active surface area of both electrode types (commercial and MC-based) was estimated by N₂ adsorption measurements performed on a Gemini VII 2390 p Series (Micromeritics), within a set of relative pressures ranging between 0.05 and 0.25 and at an evacuation rate of 133 kPa/min. Just before the measurements, the electrodes were degassed at 300 °C for 8 h, using a Micromeritics FlowPrep 060 Sample Degas System, and then weighed. The specific surface areas of the materials were calculated using the Brunauer–Emmett–Teller (BET) isotherm. These measurements revealed, for the commercial- and MC-based electrodes, a Specific Surface Area (SSA) of 1224 ± 30 m²/g and 496 ± 7 m²/g, respectively (Figures S3–S5, ESI).

3.3. Electrochemical Measurements

Electrochemical measurements were carried out in symmetric CR2032 coin cells (fabricated with the free-standing electrodes soaked in 1 M TEABF₄ in acetonitrile), using a Metrohm-Autolab potentiostat/galvanostat (PGSTAT302N) controlled by NOVA 2.1 software. To minimize contact resistances in the system, the connection of the cells’ terminals to the instrument was reinforced with copper tape. The cells were first stabilized by cycling voltammetry, with 60 wetting cycles performed at 30 mV/s between 0 and 2.5 V. Next, each cell was tested within this same range at varying scan rates (5–100 mV/s), and then galvanostatic charge–discharge tests were carried out (also from 0 to 2.5 V) at several current densities (0.1–2.5 A/g). Only the 10th voltammogram/charge–discharge cycle was considered in the calculations. Finally, the cells were also tested by potentiostatic electrochemical impedance spectroscopy (EIS), at 0 V, with a 10 mV amplitude, from 1 MHz to 40 mHz.

The capacitance of each cell ${C_{ }}_{}\left[\mathrm{F}\right]$, the specific capacitance of the material $C_{\mathrm{s}\mathrm{p}}$ [F/g], the areal capacitance $C_{\mathrm{a}}$ [F/cm²], the energy density $E_{\mathrm{s}\mathrm{p}}[\mathrm{W}\mathrm{h}/\mathrm{k}\mathrm{g}]$ and the power density $P_{\mathrm{s}\mathrm{p}}[\mathrm{k}\mathrm{W}/\mathrm{k}\mathrm{g}]$ during galvanostatic discharge were calculated, respectively, via Equations (1)–(5):

$${C_{}}_{}=\frac{i\Delta t}{\Delta V}$$

(1)

$${C_{\mathrm{s}\mathrm{p}}}_{}=\frac{4C}{m}$$

(2)

$${C_{\mathrm{a}}}_{}=\frac{C}{A}$$

(3)

$$E_{\mathrm{s}\mathrm{p}}=\frac{0.5C_{}{\Delta V}^2}{3.6m}$$

(4)

$$P_{\mathrm{s}\mathrm{p}}=\frac{{3.6E}_{\mathrm{s}\mathrm{p}}}{\Delta t}$$

(5)

where $i$ is the (constant) value of the discharging current, $\Delta t$ is the discharge time, $\Delta V$ is the difference between the cell voltage at the end and in the beginning of the discharge (after the voltage drop), $m$ (in g) is the total mass of both electrodes (i.e., considering carbon and the binder) and $A$ is the footprint area of the cell (ca. 2 cm²). The “fill factors” ($FF$) were obtained with Equation (6):

$$FF=\frac{{\int }_{t_0}^{t_{\mathrm{f}}}i\left(t\right)dV\left(t\right)}{∆V(i_{\mathrm{m}\mathrm{a}\mathrm{x}}-i_{\mathrm{m}\mathrm{i}\mathrm{n}})}$$

(6)

where $t_0$ and $t_{\mathrm{f}}$ are, respectively, the instant when the cycle begins and that when it finishes; $i$ is the instantaneous current and $dV$ is the voltage step (which depends on the scan rate and which is positive in the forward sweep and negative in the backwards sweep) and $i_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $i_{\mathrm{m}\mathrm{i}\mathrm{n}}$ are, respectively, the maximum and the minimum currents recorded during the cyclic voltammetry.

4. Conclusions

Methane cracking is an attractive route for obtaining hydrogen since, besides having a lower standard reaction enthalpy than hydrogen combustion (38 kJ/mol of H₂ against 286 kJ/mol, respectively [35]), its only by-product is solid carbon. This work has demonstrated that this by-product may be a suitable active material for high mass loading supercapacitors operating at high current densities. High mass loading supercapacitors (ca. 30 mg/cm²) prepared with this carbon showed a high rate capability: 74% of capacitance retention from 6 mA/cm² to 60 mA/cm² and a Ragone plot’s slope of −7 Wh/kW (compared to 42% and −31 Wh/kW, respectively, for high mass loading devices fabricated with commercial carbon). These promising preliminary results are attributed to carbon nanotubes (resulting from the MC process), which, despite their relatively low surface area, may facilitate the charge transport within the electrode. However, this hypothesis should be further confirmed. One possible way to do this would be to add the same amount of CNTs to the commercial carbon and assess whether the performance would be comparable to that of the MC-recovered carbon. Also, very importantly, the suitability of this by-product as a supercapacitor material should be confirmed, in the future, with cyclability tests. Moreover, a new furnace design is required to avoid the usage of quartz wool (since it negatively affects the performance of MC-recovered carbon). In case this proves technically challenging and in case it remains impossible to completely filter out these unintended fibers, these might be tentatively dissolved (using, for instance, HF/HNO₃ [36]). Furthermore, the MC parameters (reaction time, flow rate, catalyst loading and composition, surface area of the carbon support, etc.) could be optimized to tailor the properties of the generated carbon nanotubes (e.g., length, diameter) to enable the fabrication of supercapacitors with even better performances. Studies of devices with commercial-like mass loadings are currently in significant demand by the energy storage manufacturing sector (e.g., electric vehicles) [37], and thus, in the future, it would be interesting to study a range of different mass loadings and assess their impact on the capacitive performance of cells prepared with this MC-recovered carbon.