Paramagnetic Nuclear Magnetic Resonance: The Toolkit
Abstract
:1. Who
2. What
- (a)
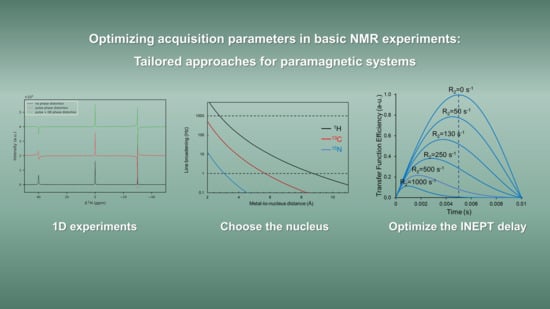
- One-dimensional experiments: fast relaxation and large spectral widths
- (b)
- Two-dimensional homonuclear 1H-1H experiments
- (c)
- Two-dimensional heteronuclear 1H-15N/1H-13C experiments
- (d)
- Relaxation rate measurements
- (e)
- 13C direct detected experiments
- (f)
- Multidimensional triple-resonance experiments
3. When/Where
3.1. One-Dimensional Experiments: Fast Relaxation and Large Spectral Widths
3.1.1. When Relaxation Is Fast
3.1.2. When the Shifts Are Large
3.2. Two-Dimensional Homonuclear 1H-1H Experiments
3.3. Two-Dimensional Heteronuclear 1H-15N/1H-13C Experiments
3.3.1. Fast Relaxing Signals Require Faster Experiments
3.3.2. Antiphase Detection: Saving Time to Preserve Signals
3.4. Relaxation Rate Measurements
3.5. 13C Direct Detected Experiments
3.6. Multidimensional Triple-Resonance Experiments
4. Why
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- La Mar, G.N.; Horrocks, W.D., Jr.; Allen, L.C. Isotropic Proton Resonance Shifts of Some Bis-(triarylphosphine) Complexes of Cobalt(II) and Nickel(II) Dihalides. J. Chem. Phys. 1964, 41, 2126–2134. [Google Scholar] [CrossRef]
- Thwaites, J.D.; Bertini, I.; Sacconi, L. Proton resonance studies of the solution equilibria of nickel(II) complexes with Schiff bases formed from salicylaldehydes and N,N-substituted ethylenediamines. II. Inorg. Chem. 1966, 5, 1036–1041. [Google Scholar] [CrossRef]
- Holm, R.H.; Everett, G.W.; Horrocks, W.D., Jr. Isotropic Nuclear Magnetic Resonance Shifts in Tetrahedral Bispyridine and Bispicoline Complexes of Nickel(II). J. Am. Chem. Soc. 1966, 88, 1071. [Google Scholar] [CrossRef]
- Kowalsky, A.J. Nuclear Magnetic Resonance Studies of Protein. J. Biol. Chem. 1962, 237, 1807–1819. [Google Scholar] [CrossRef] [PubMed]
- La Mar, G.N.; Sacconi, L. The influence of halogen, substituent and solvent on spin delocalization in high-spin, five-coordinated 2,6-diacetylpyridinebis(N-alkylimine) nickel dihalides. J. Am. Chem. Soc. 1968, 90, 7216–7223. [Google Scholar] [CrossRef]
- Parigi, G.; Ravera, E.; Piccioli, M.; Luchinat, C. Paramagnetic NMR restraints for the characterization of protein structural rearrangements. Curr. Opin. Struct. Biol. 2023, 80, 102595. [Google Scholar] [CrossRef]
- Bertini, I.; Luchinat, C. NMR of Paramagnetic Molecules in Biological Systems; Benjamin/Cummings: Menlo Park, CA, USA, 1986. [Google Scholar]
- Bertini, I.; Luchinat, C.; Parigi, G.; Ravera, E. NMR of Paramagnetic Molecules: Applications to Metallobiomolecules and Models; Elsevier: Amsterdam, The Netherlands, 2016; Volume 2. [Google Scholar]
- Ravera, E.; Gigli, L.; Fiorucci, L.; Luchinat, C.; Parigi, G. The evolution of paramagnetic NMR as a tool in structural biology. Phys. Chem. Chem. Phys. 2022, 24, 17397–17416. [Google Scholar] [CrossRef]
- Patt, S.L.; Sykes, B.D. Water eliminated Fourier transform NMR spectroscopy. J. Chem. Phys. 1972, 56, 3182. [Google Scholar] [CrossRef]
- Inubushi, T.; Becker, E.D. Efficient detection of paramagnetically shifted NMR resonances by optimizing the WEFT pulse sequence. J. Magn. Reson. 1983, 51, 128–133. [Google Scholar] [CrossRef]
- Hochmann, J.; Kellerhals, H. Proton NMR on deoxyhemoglobin: Use of a modified DEFT technique. J. Magn. Reson. 1980, 38, 23–39. [Google Scholar] [CrossRef]
- Bondon, A.; Mouro, C. PASE (PAramagetic Signal Enhancement): A New Method for NMR Study of Paramagnetic Proteins. J. Magn. Reson. 1998, 134, 154–157. [Google Scholar] [CrossRef]
- Helms, G.; Satterlee, J.D. Keeping PASE with WEFT: SHWEFT-PASE pulse sequences for H-1 NMR spectra of highly paramagnetic molecules. Magn. Reson. Chem. 2013, 51, 222–229. [Google Scholar] [CrossRef]
- Levitt, M.H.; Freeman, R.; Frenkiel, T. Broadband heteronuclear decoupling. J. Magn. Reson. 1982, 47, 328–330. [Google Scholar] [CrossRef]
- Solomon, I. Relaxation processes in a system of two spins. Phys. Rev. 1955, 99, 559–565. [Google Scholar] [CrossRef]
- Bloembergen, N. Comments on “Proton relaxation times in paramagnetic solutions”. J. Chem. Phys. 1957, 27, 575–596. [Google Scholar] [CrossRef]
- Gueron, M. Nuclear relaxation in macromolecules by paramagnetic ions: A novel mechanism. J. Magn. Reson. 1975, 19, 58–66. [Google Scholar] [CrossRef]
- Vega, A.J.; Fiat, D. Nuclear Relaxation Processes of Paramagnetic Complexes. Slow. Motion Case. Mol. Phys. 1976, 31, 347–355. [Google Scholar]
- Geraldes, C.F.G.C.; Luchinat, C. Lanthanides as shift and relaxation agents in elucidating the structure of proteins and nucleic acids. In The Lanthanides and Their Interrelations with Biosystems; CRC Press: Boca Raton, FL, USA, 2003; Volume 40, pp. 513–588. [Google Scholar]
- Gigli, L.; Di Grande, S.; Ravera, E.; Parigi, G.; Luchinat, C. NMR for Single Ion Magnets. Magnetochemistry 2021, 7, 96. [Google Scholar] [CrossRef]
- Neuhaus, D.; Williamson, M. The Nuclear Overhauser Effect in Structural and Conformational Analysis; VCH: New York, NY, USA, 1989. [Google Scholar]
- Lecomte, J.T.J.; Unger, S.W.; La Mar, G.N. Practical Considerations for the Measurements of the Homonuclear Overhauser Effect on Strongly Relaxed Protons in Paramagnetic Proteins. J. Magn. Reson. 1991, 94, 112–122. [Google Scholar] [CrossRef]
- Dugad, L.B.; La Mar, G.N.; Banci, L.; Bertini, I. Identification of localized redox states in plant-type two-iron ferredoxins using the nuclear overhauser effect. Biochemistry 1990, 29, 2263–2271. [Google Scholar] [CrossRef]
- Ramaprasad, S.; Johnson, R.D.; La Mar, G.N. 1H-NMR Nuclear Overhauser Enhancement and Paramagnetic Relaxation Determination of Peak Assignment and the Orientation of Ile-99 FG5 in Metcyanomyoglobin. J. Am. Chem. Soc. 1984, 106, 5330–5335. [Google Scholar] [CrossRef]
- de Ropp, J.S.; Thanabal, V.; La Mar, G.N. NMR Evidence for a Horseradish Peroxidase State with a Deprotonated Proximal Histidine. J. Am. Chem. Soc. 1985, 107, 8268–8270. [Google Scholar] [CrossRef]
- Lecomte, J.T.J.; La Mar, G.N. The homonuclear overhauser effect in H2O solution of low-spin hemeproteins. Assignment of protons in the heme cavity of sperm whale myoglobin. Eur. Biophys. J. 1986, 13, 373–381. [Google Scholar] [CrossRef] [PubMed]
- Santos, H.; Turner, D.L.; Xavier, A.V.; LeGall, J. Two-Dimensional NMR Studies of Electron Transfer in Cytochrome c3. J. Magn. Reson. 1984, 59, 177–180. [Google Scholar] [CrossRef]
- Ravera, E.; Gigli, L.; Czarniecki, B.; Lang, L.; Kummerle, R.; Parigi, G.; Piccioli, M.; Neese, F.; Luchinat, C. A Quantum Chemistry View on Two Archetypical Paramagnetic Pentacoordinate Nickel(II) Complexes Offers a Fresh Look on Their NMR Spectra. Inorg. Chem. 2021, 60, 2068–2075. [Google Scholar] [CrossRef]
- Banci, L.; Luchinat, C. Selective versus non-selective T1 experiments to determine metal-nucleus distances in paramagnetic proteins. Inorg. Chim. Acta 1998, 275–276, 373–379. [Google Scholar] [CrossRef]
- Santana, F.S.; Perfetti, M.; Briganti, M.; Sacco, F.; Poneti, G.; Ravera, E.; Soares, J.F.; Sessoli, R. A dysprosium single molecule magnet outperforming current pseudocontact shift agents. Chem. Sci. 2022, 13, 5860–5871. [Google Scholar] [CrossRef] [PubMed]
- Gregory, R.M.; Bain, A.D. The effects of finite rectangular pulses in NMR: Phase and intensity distortions for a spin-1/2. Concepts Magn. Reson. Part A 2009, 34A, 305–314. [Google Scholar] [CrossRef]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ravera, E. Phase distortion-free paramagnetic NMR spectra. J. Magn. Reson. Open 2021, 8–9, 100022. [Google Scholar] [CrossRef]
- Aue, W.P.; Bartholdi, E.; Ernst, R.R. Two-dimensional spectroscopy. Application to nuclear magnetic resonance. J. Chem. Phys. 1976, 64, 2229–2235. [Google Scholar] [CrossRef]
- Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Oxford University Press: London, UK, 1987. [Google Scholar]
- Wüthrich, K. NMR of Proteins and Nucleic Acids; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Keeler, J. Understanding NMR Spectroscopy; Wiley: London, UK, 2011; p. 526. [Google Scholar]
- Macura, S.; Ernst, R.R. Elucidation of cross relaxation in liquids by two-dimensional N.M.R. spectroscopy. Mol. Phys. 1980, 41, 95. [Google Scholar] [CrossRef]
- Bax, A.; Davis, D.G. Practical aspects of two-dimensional transverse NOE spectroscopy. J. Magn. Reson. 1985, 63, 207–213. [Google Scholar] [CrossRef]
- Simonis, U.; Dallas, J.L.; Walker, F.A. ROESY: A technique for establishing the existence of chemical exchange in paramagnetic model hemes with short T1 and T2 relaxation times. Inorg. Chem. 1992, 31, 5349–5350. [Google Scholar] [CrossRef]
- Borgias, B.; Thomas, P.D.; James, T.L. Complete Relaxation Matrix Analysis (CORMA). 5.0; University of California: San Francisco, CA, USA, 1989. [Google Scholar]
- Sørensen, O.W.; Eich, G.W.; Levitt, M.H.; Bodenhausen, G.; Ernst, R.R. Product Operator Formalism for the Description of NMR Pulse Experiments. Progr. NMR Spectrosc. 1983, 16, 163–192. [Google Scholar] [CrossRef]
- Shriver, J. Product operators and coherence transfer in multiple-pulse NMR experiments. Concepts Magn. Reson. 1992, 4, 1–34. [Google Scholar] [CrossRef]
- Bertini, I.; Luchinat, C.; Tarchi, D. Are true scalar proton-proton connectivities ever measured in COSY spectra of paramagnetic macromolecules? Chem. Phys. Lett. 1993, 203, 445–449. [Google Scholar] [CrossRef]
- Qin, J.; Delaglio, F.; La Mar, G.N.; Bax, A. Distinguishing the Effects of Cross Correlation and J Coupling in COSY Spectra of Paramagnetic Protein. J. Magn. Reson. Ser. B 1993, 102, 332–336. [Google Scholar] [CrossRef]
- Werbelow, L.G. Cross-Correlation and Interference Terms. In Encyclopedia of Nuclear Magnetic Resonance; Grant, D.M., Harris, R.K., Eds.; Wiley: Chichester, UK, 1996; pp. 4072–4079. [Google Scholar]
- Luchinat, C.; Steuernagel, S.; Turano, P. Application of 2D-NMR techniques to paramagnetic systems. Inorg. Chem. 1990, 29, 4351–4353. [Google Scholar] [CrossRef]
- Cavanagh, J.; Fairbrother, W.J.; Palmer, A.G., III; Rance, M.; Skelton, N.J. Protein NMR Spectroscopy. Principles and Practice; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Morris, G.A.; Freeman, R. Enhancement of Nuclear Magnetic Resonance Signals by Polarization Transfer. J. Am. Chem. Soc. 1979, 101, 760–762. [Google Scholar] [CrossRef]
- Bodenhausen, G.; Ruben, D.J. Natural abundance nitrogen-15 NMR by enhanced heteronuclear spectroscopy. Chem. Phys. Lett. 1980, 69, 185–188. [Google Scholar] [CrossRef]
- Werbelow, L.; Thevand, A. Anomalous Nuclear Spin Relaxation Effects in the Presence of Paramagnetic Substances. J. Magn. Reson. Ser. A 1993, 101, 317–319. [Google Scholar] [CrossRef]
- Santos, H.; Turner, D.L. 13C and proton NMR studies of horse ferricytochrome c. FEBS Lett. 1986, 194, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Bermel, W.; Bertini, I.; Felli, I.C.; Pierattelli, R. Speeding up 13C direct detection Biomolecular NMR experiments. J. Am. Chem. Soc. 2009, 131, 15339–15345. [Google Scholar] [CrossRef] [PubMed]
- Grifagni, D.; Silva, J.M.; Cantini, F.; Piccioli, M.; Banci, L. Relaxation-based NMR assignment: Spotlights on ligand binding sites in human CISD3. J. Inorg. Biochem. 2023, 239, 112089. [Google Scholar] [CrossRef] [PubMed]
- Bertini, I.; Donaire, A.; Luchinat, C.; Rosato, A. Paramagnetic relaxation as a tool for solution structure determination: Clostridium pasterianum ferredoxin as an example. Proteins Struct. Funct. Genet. 1997, 29, 348–358. [Google Scholar] [CrossRef]
- Clore, G.M. Practical Aspects of Paramagnetic Relaxation Enhancement in Biological Macromolecules. Methods Enzym. 2015, 564, 485–497. [Google Scholar]
- Iwahara, J.; Clore, G.M. Detecting transient intermediates in macromolecular binding by paramagnetic NMR. Nature 2006, 440, 1227–1230. [Google Scholar] [CrossRef]
- Tang, C.; Ghirlando, R.; Clore, G.M. Visualization of Transient Ultra-Weak Protein Self-Association in Solution Using Paramagnetic Relaxation Enhancement. J. Am. Chem. Soc. 2008, 130, 4048–4056. [Google Scholar] [CrossRef]
- Chen, Z.G.; de Ropp, J.S.; Hernandez, G.; La Mar, G.N. 2D NMR approaches to characterizing the molecular structure and dynamic stability of the active site for cyanide-inhibited horseradish peroxidase. J. Am. Chem. Soc. 1994, 116, 8772–8783. [Google Scholar] [CrossRef]
- Ciofi-Baffoni, S.; Gallo, A.; Muzzioli, R.; Piccioli, M. The IR-15N-HSQC-AP experiment: A new tool for NMR spectroscopy of paramagnetic molecules. J. Biomol. NMR 2014, 58, 123–128. [Google Scholar] [CrossRef]
- Trindade, I.B.; Invernici, M.; Cantini, F.; Louro, R.O.; Piccioli, M. PRE-driven protein NMR structures: An alternative approach in highly paramagnetic systems. FEBS J. 2021, 288, 3010–3023. [Google Scholar] [CrossRef] [PubMed]
- Donaldson, L.W.; Skrynnikov, N.R.; Choy, W.Y.; Muhandiram, D.R.; Sarkar, B.; Forman-Kay, J.D.; Kay, L.E. Structural characterization of proteins with an attached ATCUN motif by paramagnetic relaxation enhancement NMR spectroscopy. J. Am. Chem. Soc. 2001, 123, 9843–9847. [Google Scholar] [CrossRef]
- Invernici, M.; Trindade, I.B.; Cantini, F.; Louro, R.O.; Piccioli, M. Measuring transverse relaxation in highly paramagnetic systems. J. Biomol. NMR 2020, 74, 431–442. [Google Scholar] [CrossRef] [PubMed]
- Banci, L.; Brancaccio, D.; Ciofi-Baffoni, S.; Del Conte, R.; Gadepalli, R.; Mikolajczyk, M.; Neri, S.; Piccioli, M.; Winkelmann, J. [2Fe-2S] cluster transfer in iron-sulfur protein biogenesis. Proc. Natl. Acad. Sci. USA 2014, 111, 6203–6208. [Google Scholar] [CrossRef]
- Felli, I.C.; Pierattelli, R. 13C Direct Detected NMR for Challenging Systems. Chem. Rev. 2022, 122, 9468–9496. [Google Scholar] [CrossRef] [PubMed]
- Querci, L.; Trindade, I.B.; Invernici, M.; Silva, J.M.; Cantini, F.; Louro, R.O.; Piccioli, M. NMR of Paramagnetic Proteins: 13C Derived Paramagnetic Relaxation Enhancements Are an Additional Source of Structural Information in Solution. Magnetochemistry 2023, 9, 66. [Google Scholar] [CrossRef]
- Bermel, W.; Bertini, I.; Felli, I.C.; Kümmerle, R.; Pierattelli, R. 13C direct detection experiments on the paramagnetic oxidized monomeric copper, zinc superoxide dismutase. J. Am. Chem. Soc. 2003, 125, 16423–16429. [Google Scholar] [CrossRef] [PubMed]
- Querci, L.; Grifagni, D.; Trindade, I.B.; Silva, J.M.; Louro, R.O.; Cantini, F.; Piccioli, M. Paramagnetic NMR to study iron sulfur proteins: 13C detected experiments illuminate the vicinity of the metal center. J. Biomol. NMR 2023, 77, 247–259. [Google Scholar] [CrossRef]
- Mateos, B.; Conrad-Billroth, C.; Schiavina, M.; Beier, A.; Kontaxis, G.; Konrat, R.; Felli, I.C.; Pierattelli, R. The Ambivalent Role of Proline Residues in an Intrinsically Disordered Protein: From Disorder Promoters to Compaction Facilitators. J. Mol. Biol. 2020, 432, 3093–3111. [Google Scholar] [CrossRef]
- Takeuchi, K.; Gal, M.; Shimada, I.; Wagner, G. Low-g nuclei detection experiments for biomolecular NMR. In Recent Developments in Biomolecular NMR; Clore, G.M., Potts, J., Eds.; RSC Publishing: Cambridge, UK, 2012; pp. 25–52. [Google Scholar]
- Trindade, I.B.; Invernici, M.; Cantini, F.; Louro, R.O.; Piccioli, M. Sequence-specific assignments in NMR spectra of paramagnetic systems: A non-systematic approach. Inorg. Chim. Acta 2021, 514, 119984. [Google Scholar] [CrossRef]
- Clore, G.M.; Gronenborn, A.M. Structure of larger proteins in solutions: Three- and four- dimensional heteronuclear NMR spectroscopy. Science 1991, 252, 1390–1399. [Google Scholar] [CrossRef] [PubMed]
- Bertini, I.; Luchinat, C.; Rosato, A. The solution structure of paramagnetic metalloproteins. Progr. Biophys. Mol. Biol. 1996, 66, 43–80. [Google Scholar] [CrossRef] [PubMed]
- Wuthrich, K. Protein structure determination in solution by NMR spectroscopy. J. Biol. Chem. 1990, 265, 22059–22062. [Google Scholar] [CrossRef] [PubMed]
- Ott, J.C.; Wadepohl, H.; Enders, M.; Gade, L.H. Taking Solution Proton NMR to Its Extreme: Prediction and Detection of a Hydride Resonance in an Intermediate-Spin Iron Complex. J. Am. Chem. Soc. 2018, 140, 17413–17417. [Google Scholar] [CrossRef] [PubMed]
- Ott, J.C.; Suturina, E.A.; Kuprov, I.; Nehrkorn, J.; Schnegg, A.; Enders, M.; Gade, L.H. Observability of Paramagnetic NMR Signals at over 10 000 ppm Chemical Shifts. Angew. Chem. Int. Ed. Engl. 2021, 60, 22856–22864. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Smet, P.F.; Martin, L.I.D.J.; Pritzel, C.; Schmedt auf der Günne, J. Doping homogeneity in co-doped materials investigated at different length scales. Phys. Chem. Chem. Phys. 2020, 22, 818–825. [Google Scholar] [CrossRef] [PubMed]
- Novikov, V.V.; Pavlov, A.A.; Belov, A.S.; Vologzhanina, A.V.; Savitsky, A.; Voloshin, Y.Z. Transition Ion Strikes Back: Large Magnetic Susceptibility Anisotropy in Cobalt(II) Clathrochelates. J. Phys. Chem. Lett. 2014, 5, 3799–3803. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wires Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Van den Heuvel, W.; Soncini, A. NMR chemical shift as analytical derivative of the Helmholtz free energy. J. Chem. Phys. 2013, 138, 054113. [Google Scholar] [CrossRef]
- Lang, L.A.-O.; Ravera, E.A.-O.; Parigi, G.A.-O.; Luchinat, C.A.-O.; Neese, F.A.-O. Solution of a Puzzle: High-Level Quantum-Chemical Treatment of Pseudocontact Chemical Shifts Confirms Classic Semiempirical Theory. J. Phys. Chem. Lett. 2020, 11, 8735–8744. [Google Scholar] [CrossRef]
- Caillet-Saguy, C.; Piccioli, M.; Turano, P.; Lukat-Rodgers, G.; Wolff, N.; Rodgers, K.; Izadi-Pruneyre, N.; Delepierre, M.; Lecroisey, A. Heme carrier HasA: Learning about the role of the iron axial ligands in the heme uptake and release processes. J. Biol. Chem. 2012, 287, 26932–26943. [Google Scholar] [CrossRef] [PubMed]
- Neto, S.E.; Fonseca, B.M.; Maycock, C.; Louro, R.O. Analysis of the residual alignment of a paramagnetic multiheme cytochrome by NMR. Chem. Comm. 2014, 50, 4561–4563. [Google Scholar] [CrossRef]
- Fernandes, T.M.; Morgado, L.; Salgueiro, C.A.; Turner, D.L. Determination of the magnetic properties and orientation of the heme axial ligands of PpcA from Geobacter metallireducens by paramagnetic NMR. J. Inorg. Biochem. 2019, 198, 110718. [Google Scholar] [CrossRef] [PubMed]
- Kleingardner, J.G.; Bowman, S.E.J.; Bren, K.L. The Influence of Heme Ruffling on Spin Densities in Ferricytochromes c Probed by Heme Core 13C NMR. Inorg. Chem. 2013, 52, 12933–12946. [Google Scholar] [CrossRef] [PubMed]
- Worrall, J.A.; Liu, A.; Crowley, P.B.; Nocek, J.M.; Hoffman, B.M.; Ubbink, M. Myoglobin and cytochrome b5: A nuclear magnetic resonance study of a highly dynamic protein complex. Biochemistry 2002, 41, 11721–11730. [Google Scholar] [CrossRef] [PubMed]
- Banci, L.; Camponeschi, F.; Ciofi-Baffoni, S.; Piccioli, M. The NMR contribution to protein–protein networking in Fe–S protein maturation. JBIC J. Biol. Inorg. Chem. 2018, 23, 665–685. [Google Scholar] [CrossRef] [PubMed]
- Cai, K.; Markley, J.L. NMR as a Tool to Investigate the Processes of Mitochondrial and Cytosolic Iron-Sulfur Cluster Biosynthesis. Molecules 2018, 23, 2213. [Google Scholar] [CrossRef]
- Xia, B.; Jenk, D.; LeMaster, D.M.; Westler, W.M.; Markley, J.L. Electron-nuclear interactions in two prototypical [2Fe-2S] proteins: Selective (chiral) deuteration and analysis of 1H and 2H NMR signals from the alpha and beta hydrogens of cysteinyl residues that ligate the iron in the active sites of human ferredoxin and Anabaena 7120 vegetative ferredoxin. Arch. Biochem. Biophys. 2000, 373, 328–334. [Google Scholar]
- Beinert, H. Iron-sulfur proteins: Ancient structures, still full of surprises. J. Biol. Inorg. Chem. 2000, 5, 2–15. [Google Scholar] [CrossRef]
- Invernici, M.; Selvolini, G.; Silva, J.M.; Marrazza, G.; Ciofi-Baffoni, S.; Piccioli, M. Interconversion between [2Fe-2S] and [4Fe-4S] cluster glutathione complexes. Chem. Commun. 2022, 58, 3533–3536. [Google Scholar] [CrossRef]
- Blondin, G.; Girerd, J.J. Interplay of Electron Exchange and Electron-Transfer in Metal Polynuclear Complexes in Proteins or Chemical-Models. Chem. Rev. 1990, 90, 1359–1376. [Google Scholar] [CrossRef]
- Mouesca, J.-M.; Lamotte, B. Iron-Sulfur clusters and their electronic and magnetic properties. Coord. Chem. Rev. 1998, 178–180, 1573–1614. [Google Scholar] [CrossRef]
- Belinskii, M.I. Hyperfine evidence of strong double exchange in multimetallic {[Fe4S4]} active center of Escherichia coli sulfite reductase. JBIC J. Biol. Inorg. Chem. 1996, 1, 186–188. [Google Scholar] [CrossRef]
- Krishnamoorthi, R.; Markley, J.L.; Cusanovich, M.A.; Przysiecki, C.T. Hydrogen-1 nuclear magnetic resonance investigation of Clostridium pasteurianum rubredoxin: Previously unobserved signals. Biochemistry 1986, 25, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Oh, B.-H.; Markley, J.L. Multinuclear magnetic resonance studies of the 2Fe-2S* ferredoxin from Anabaena species strain PCC 7210. 3. Detection and characterization of hyperfine-shifted nitrogen-15 and hydrogen-1 resonances of the oxidized form. Biochemistry 1990, 29, 4012–4017. [Google Scholar] [CrossRef] [PubMed]
- Wilkens, S.J.; Xia, B.; Volkman, B.F.; Weinhold, F.; Markley, J.L.; Westler, W.M. Inadequacies of the Point-Dipole Approximation forDescribing Electron-Nuclear Interactions in Paramagnetic Proteins: Hybrid Density Functional Calculations and teh Analysis of NMR Relaxation of High Spin Iron(III) Rubredoxin. J. Phys. Chem. B 1998, 102, 8300–8305. [Google Scholar] [CrossRef]
- Machonkin, T.E.; Westler, W.M.; Markley, J.L. Strategy for the study of paramagnetic proteins with slow electronic relaxation rates by nmr spectroscopy: Application to oxidized human [2Fe-2S] ferredoxin. J. Am. Chem. Soc. 2004, 126, 5413–5426. [Google Scholar] [CrossRef]
- Macedo, A.L.; Moura, I.; Moura, J.J.G.; LeGall, J.; Huynh, B.H. Temperature-dependent proton NMR investigation of the electronic structure of the trinuclear iron cluster of the oxidized Desulfovibrio gigas ferredoxin II. Inorg. Chem. 1993, 32, 1101–1105. [Google Scholar] [CrossRef]
- Goodfellow, B.J.; Macedo, A.L.; Rodrigues, P.; Moura, I.; Wray, V.; Moura, J.J.G. The solution structure of a [3Fe-4S] ferredoxin: Oxidised ferredoxin II from Desulfovibrio gigas. J. Biol. Inorg. Chem. 1999, 4, 421–430. [Google Scholar] [CrossRef]
- Teixeira, M.; Batista, R.; Campos, A.P.; Gomes, C.; Mendes, J.; Pacheco, I.; Anemuller, S.; Hagen, W.R. A seven-iron ferredoxin from the thermoacidophilic archaeon Desulfurolobus ambivalens. Eur. J. Biochem. 1995, 227, 322–327. [Google Scholar] [CrossRef]
- Camponeschi, F.; Piccioli, M.; Banci, L. The Intriguing mitoNEET: Functional and Spectroscopic Properties of a Unique [2Fe-2S] Cluster Coordination Geometry. Molecules 2022, 27, 8218. [Google Scholar] [CrossRef] [PubMed]
- Camponeschi, F.; Gallo, A.; Piccioli, M.; Banci, L. The long-standing relationship between Paramagnetic NMR and Iron-Sulfur proteins: The mitoNEET example. An old method for new stories or the other way around? Magn. Reson. Discuss. 2021, 2, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Trindade, I.B.; Hernandez, G.; Lebegue, E.; Barriere, F.; Cordeiro, T.; Piccioli, M.; Louro, R.O. Conjuring up a ghost: Structural and functional characterization of FhuF, a ferric siderophore reductase from E. coli. J. Biol. Inorg. Chem. 2021, 26, 313–326. [Google Scholar] [CrossRef] [PubMed]
- Camponeschi, F.; Ciofi-Baffoni, S.; Calderone, V.; Banci, L. Molecular Basis of Rare Diseases Associated to the Maturation of Mitochondrial [4Fe-4S]-Containing Proteins. Biomolecules 2022, 12, 1009. [Google Scholar] [CrossRef]
- Paquete, C.M.; Saraiva, I.H.; Calçada, E.; Louro, R.O. Molecular basis for directional electron transfer. J. Biol. Chem. 2010, 285, 10370–10375. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Serres, R.; Clemancey, M.; Latour, J.M.; Blondin, G. Contribution of Mossbauer spectroscopy to the investigation of Fe/S biogenesis. J. Biol. Inorg. Chem. 2018, 23, 635–644. [Google Scholar] [CrossRef] [PubMed]
- Welegedara, A.P.; Yang, Y.; Lee, M.D.; Swarbrick, J.D.; Huber, T.; Graham, B.; Goldfarb, D.; Otting, G. Double-Arm Lanthanide Tags Deliver Narrow Gd3+-Gd3+ Distance Distributions in Double Electron-Electron Resonance (DEER) Measurements. Chem-Eur. J. 2017, 23, 11694–11702. [Google Scholar] [CrossRef]
- Srour, B.; Gervason, S.; Hoock, M.H.; Monfort, B.; Want, K.A.-O.; Larkem, D.; Trabelsi, N.; Landrot, G.A.-O.X.; Zitolo, A.A.-O.; Fonda, E.A.-O.; et al. Iron Insertion at the Assembly Site of the ISCU Scaffold Protein Is a Conserved Process Initiating Fe-S Cluster Biosynthesis. J. Am. Chem. Soc. 2022, 144, 17496–17515. [Google Scholar] [CrossRef]
- Camponeschi, F.; Muzzioli, R.; Ciofi-Baffoni, S.; Piccioli, M.; Banci, L. Paramagnetic 1H NMR Spectroscopy to Investigate the Catalytic Mechanism of Radical S-Adenosylmethionine Enzymes. J. Mol. Biol. 2019, 431, 4514–4522. [Google Scholar] [CrossRef]
- Honarmand Ebrahimi, K.; Ciofi-Baffoni, S.; Hagedoorn, P.L.; Nicolet, Y.; Le Brun, N.E.; Hagen, W.R.; Armstrong, F.A. Iron-sulfur clusters as inhibitors and catalysts of viral replication. Nat. Chem. 2022, 14, 253–266. [Google Scholar] [CrossRef]
- Brancaccio, D.; Gallo, A.; Piccioli, M.; Novellino, E.; Ciofi-Baffoni, S.; Banci, L. [4Fe-4S] Cluster Assembly in Mitochondria and Its Impairment by Copper. J. Am. Chem. Soc. 2017, 139, 719–730. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Wei, L.; Da, A.; Stark, H.; Hagedoorn, P.L.; Ciofi-Baffoni, S.; Cowley, S.A.; Louro, R.O.; Todorovic, S.; Mroginski, M.A.; et al. Radical-SAM dependent nucleotide dehydratase (SAND), rectification of the names of an ancient iron-sulfur enzyme using NC-IUBMB recommendations. Front. Mol. Biosci. 2022, 9, 1032220. [Google Scholar] [CrossRef] [PubMed]
- Bennett, S.P.; Crack, J.C.; Puglisi, R.; Pastore, A.; Le Brun, N.E. Native mass spectrometric studies of IscSU reveal a concerted, sulfur-initiated mechanism of iron-sulfur cluster assembly. Chem. Sci. 2022, 14, 78–95. [Google Scholar] [CrossRef] [PubMed]
- Gervason, S.; Larkem, D.; Mansour, A.B.; Botzanowski, T.; Muller, C.S.; Pecqueur, L.; Le Pavec, G.; Delaunay-Moisan, A.; Brun, O.; Agramunt, J.; et al. Physiologically relevant reconstitution of iron-sulfur cluster biosynthesis uncovers persulfide-processing functions of ferredoxin-2 and frataxin. Nat. Commun. 2019, 10, 3566. [Google Scholar] [CrossRef] [PubMed]
- Bubacco, L.; Salgado, J.; Tepper, A.W.J.W.; Vijgenboom, E.; Canters, G.W. 1H NMR spectroscopy of the binuclear Cu(II) active site of Streptomyces antibioticus tyrosinase. FEBS Lett. 1999, 442, 215–220. [Google Scholar] [CrossRef]
- Zaballa, M.-E.; Ziegler, L.; Kosman, D.J.; Vila, A.J. NMR Study of the Exchange Coupling in the Trinuclear Cluster of the Multicopper Oxidase Fet3p. J. Am. Chem. Soc. 2010, 132, 11191–11196. [Google Scholar] [CrossRef] [PubMed]
- Machczynski, M.C.; Babicz, J.T. Correlating the structures and activities of the resting oxidized and native intermediate states of a small laccase by paramagnetic NMR. J. Inorg. Biochem. 2016, 159, 62–69. [Google Scholar] [CrossRef]
- Arnesano, F.; Banci, L.; Bertini, I.; Felli, I.C.; Luchinat, C.; Thompsett, A.R. A strategy for the NMR characterization of type II copper(II) proteins: The case of the copper trafficking protein CopC from Pseudomonas Syringae. J. Am. Chem. Soc. 2003, 125, 7200–7208. [Google Scholar] [CrossRef]
- Abelein, A.; Ciofi-Baffoni, S.; Mörman, C.; Kumar, R.; Giachetti, A.; Piccioli, M.; Biverstål, H. Molecular Structure of Cu(II)-Bound Amyloid-β Monomer Implicated in Inhibition of Peptide Self-Assembly in Alzheimer’s Disease. JACS Au 2022, 2, 2571–2584. [Google Scholar] [CrossRef]
- Scanu, S.; Foerster, J.M.; Ullmann, G.M.; Ubbink, M. Role of Hydrophobic Interactions in the Encounter Complex Formation of the Plastocyanin and Cytochrome f Complex Revealed by Paramagnetic NMR Spectroscopy. J. Am. Chem. Soc. 2013, 135, 7681–7692. [Google Scholar] [CrossRef]
- Correa, J.; Garcia-Barandela, A.; Socias-Pinto, L.; Fernandez-Megia, E. Filtering the NMR Spectra of Mixtures by Coordination to Paramagnetic Cu2+. Anal. Chem. 2022, 94, 10907–10911. [Google Scholar] [CrossRef] [PubMed]
- Miao, Q.; Nitsche, C.; Orton, H.; Overhand, M.; Otting, G.; Ubbink, M. Paramagnetic Chemical Probes for Studying Biological Macromolecules. Chem. Rev. 2022, 122, 9571–9642. [Google Scholar] [CrossRef] [PubMed]
- Luchinat, C.; Soriano, A.; Djinovic-Carugo, K.; Saraste, M.; Malmström, B.G.; Bertini, I. Electronic and geometric structure of the CuA site studied by 1H NMR in a soluble domain of cytochrome c oxidase from Paracoccus denitrificans. J. Am. Chem. Soc. 1997, 119, 11023–11027. [Google Scholar] [CrossRef]
- Salgado, J.; Warmerdam, G.; Bubacco, L.; Canters, G.W. Understanding the electronic properties of the CuA site from the soluble domain of cytochrome c oxidase through paramagnetic 1H NMR. Biochemistry 1998, 37, 7378–7389. [Google Scholar] [CrossRef] [PubMed]
- Fernández, C.O.; Cricco, J.A.; Slutter, C.E.; Richards, J.H.; Gray, H.B.; Vila, A.J. Axial ligand modulation of the electronic structures of binuclear copper sites: Analysis of paramagnetic 1H NMR spectra of Met160Gln CuA. J. Am. Chem. Soc. 2001, 123, 11678–11685. [Google Scholar] [CrossRef]
- Abriata, L.A.; Ledesma, G.N.; Pierattelli, R.; Vila, A.J. Electronic structure of the ground and excited states of the CuA site by NMR spectroscopy. J. Am. Chem. Soc. 2009, 131, 1939–1946. [Google Scholar] [CrossRef]
- Spronk, C.; Zerko, S.; Gorka, M.; Kozminski, W.; Bardiaux, B.; Zambelli, B.; Musiani, F.; Piccioli, M.; Basak, P.; Blum, F.C.; et al. Structure and dynamics of Helicobacter pylori nickel-chaperone HypA: An integrated approach using NMR spectroscopy, functional assays and computational tools. J. Biol. Inorg. Chem. 2018, 23, 1309–1330. [Google Scholar] [CrossRef]
- Zambelli, B.; Basak, P.; Hu, H.; Piccioli, M.; Musiani, F.; Broll, V.; Imbert, L.; Boisbouvier, J.; Maroney, M.J.; Ciurli, S. The structure of the high-affinity nickel-binding site in the Ni,Zn-HypA•UreE2 complex. Metallomics 2023, 15, mfad003. [Google Scholar] [CrossRef]
- Bertini, I.; Luchinat, C. Cobalt(II) as a probe of the structure and function of carbonic anhydrase. Acc. Chem. Res. 1983, 16, 272–279. [Google Scholar] [CrossRef]
- Cerofolini, L.; Staderini, T.; Giuntini, S.; Ravera, E.; Fragai, M.; Parigi, G.; Pierattelli, R.; Luchinat, C. Long-range paramagnetic NMR data can provide a closer look on metal coordination in metalloproteins. J. Biol. Inorg. Chem. 2018, 23, 71–80. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, D.T.; Gronenborn, A.M. Ligand-Capped Cobalt(II) Multiplies the Value of the Double-Histidine Motif for PCS NMR Studies. J. Am. Chem. Soc. 2023, 145, 4564–4569. [Google Scholar] [CrossRef] [PubMed]
- Herath, I.D.; Breen, C.; Hewitt, S.H.; Berki, T.R.; Kassir, A.F.; Dodson, C.; Judd, M.; Jabar, S.; Cox, N.; Otting, G.; et al. A Chiral Lanthanide Tag for Stable and Rigid Attachment to Single Cysteine Residues in Proteins for NMR, EPR and Time-Resolved Luminescence Studies. Chemistry 2021, 27, 13009–13023. [Google Scholar] [CrossRef] [PubMed]
- Nitsche, C.; Otting, G. Intrinsic and Extrinsic Paramagnetic Probes. In Paramagnetism in Experimental Biomolecular NMR; Luchinat, C., Parigi, G., Ravera, E., Eds.; Royal Society of Chemistry: Cambridge, UK, 2018; Volume 1, pp. 189–218. [Google Scholar]
- Miao, Q.; Liu, W.M.; Kock, T.; Blok, A.; Timmer, M.; Overhand, M.; Ubbink, M. A Double-Armed, Hydrophilic Transition Metal Complex as a Paramagnetic NMR Probe. Angew. Chem. Int. Ed. Engl. 2019, 58, 13093–13100. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.J.; Rieder, P.S.; Abiko, L.A.; Rossler, P.; Gossert, A.D.; Haussinger, D.; Grzesiek, S. Nanobody GPS by PCS: An Efficient New NMR Analysis Method for G Protein Coupled Receptors and Other Large Proteins. J. Am. Chem. Soc. 2022, 144, 21728–21740. [Google Scholar] [CrossRef]
- Muntener, T.; Joss, D.; Haussinger, D.; Hiller, S. Pseudocontact Shifts in Biomolecular NMR Spectroscopy. Chem. Rev. 2022, 122, 9422–9467. [Google Scholar] [CrossRef]
- Parker, D.; Suturina, E.A.; Kuprov, I.; Chilton, N.F. How the Ligand Field in Lanthanide Coordination Complexes Determines Magnetic Susceptibility Anisotropy, Paramagnetic NMR Shift, and Relaxation Behavior. Acc. Chem. Res. 2020, 53, 1520–1534. [Google Scholar] [CrossRef]
- Mori, M.; Kateb, F.; Bodenhausen, G.; Piccioli, M.; Abergel, D. Towards structural dynamics: Protein motions viewed by chemical shift modulations and direct detection of C’N multiple-quantum relaxation. J. Am. Chem. Soc. 2010, 132, 3594–3600. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Querci, L.; Fiorucci, L.; Ravera, E.; Piccioli, M. Paramagnetic Nuclear Magnetic Resonance: The Toolkit. Inorganics 2024, 12, 15. https://doi.org/10.3390/inorganics12010015
Querci L, Fiorucci L, Ravera E, Piccioli M. Paramagnetic Nuclear Magnetic Resonance: The Toolkit. Inorganics. 2024; 12(1):15. https://doi.org/10.3390/inorganics12010015
Chicago/Turabian StyleQuerci, Leonardo, Letizia Fiorucci, Enrico Ravera, and Mario Piccioli. 2024. "Paramagnetic Nuclear Magnetic Resonance: The Toolkit" Inorganics 12, no. 1: 15. https://doi.org/10.3390/inorganics12010015
APA StyleQuerci, L., Fiorucci, L., Ravera, E., & Piccioli, M. (2024). Paramagnetic Nuclear Magnetic Resonance: The Toolkit. Inorganics, 12(1), 15. https://doi.org/10.3390/inorganics12010015