Field-Induced Slow Relaxation in a Dinuclear Dysprosium(III) Complex Based on 3-Methoxycinnamic Acid
Abstract
:1. Introduction
2. Results
2.1. Synthesis and Crystal Structure
2.2. DC Magnetic Properties
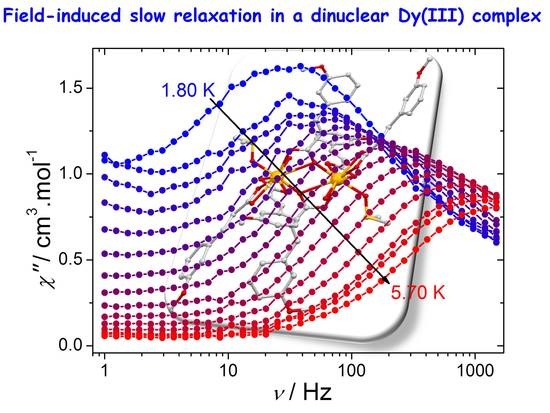
2.3. AC Magnetic Properties
3. Discussion
4. Materials and Methods
4.1. Synthesis and Crystal Structure
4.2. Magnetic Measurements
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.-Y.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Luzon, J.; Sessoli, R. Lanthanides in molecular magnetism: So fascinating, so challenging. Dalton Trans. 2012, 41, 13556–13567. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide single-molecule magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Troiani, F.; Affronte, M. Molecular spins for quantum information technologies. Chem. Soc. Rev. 2011, 40, 3119–3129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, Y.-C.; Liu, J.-L.; Vieru, V.; Ungur, L.; Jia, J.-H.; Chibotaru, L.F.; Lan, Y.; Wernsdorfer, W.; Gao, S.; et al. A stable pentagonal bipyramidal Dy(III) single-ion magnet with a record magnetization reversal barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.K.; Rajeshkumar, T.; Rajaraman, G.; Murugavel, R. An air-stable Dy(III) single-ion magnet with high anisotropy barrier and blocking temperature. Chem. Sci. 2016, 7, 5181–5191. [Google Scholar] [CrossRef]
- Ungur, L.; Chibotaru, L.F. Strategies toward high-temperature lanthanide-based single-molecule magnets. Inorg. Chem. 2016, 55, 10043–10056. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamaki, A.; Layfield, R.A. A dysprosium metallocene single-molecule magnet functioning at the axial limit. Angew. Chem. Int. Ed. Engl. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Bernot, K.; Golhen, S.; Le Guennic, B.; Guizouarn, T.; Ouahab, L.; Cador, O. Magnetic memory in an isotopically enriched and magnetically isolated mononuclear dysprosium complex. Angew. Chem. Int. Ed. 2015, 54, 1504–1507. [Google Scholar] [CrossRef] [PubMed]
- Blagg, R.J.; Ungur, L.; Tuna, F.; Speak, J.; Comar, P.; Collison, D.; Wernsdorfer, W.; McInnes, E.J.L.; Chibotaru, L.F.; Winpenny, R.E.P. Magnetic relaxation pathways in lanthanide single-molecule magnets. Nat. Chem. 2013, 5, 673–678. [Google Scholar] [CrossRef] [PubMed]
- Moreno Pineda, E.; Chilton, N.F.; Marx, R.; Dörfel, M.; Sells, D.O.; Neugebauer, P.; Jiang, S.-D.; Collison, D.; van Slageren, J.; McInnes, E.J.L.; et al. Direct measurement of dysprosium(III)···dysprosium(III) interactions in a single-molecule magnet. Nat. Comm. 2014, 5, 5243. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Habib, F.; Lin, P.-H.; Korobkov, I.; Enright, G.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Murugesu, M. Single-molecule magnet behavior for an antiferromagnetically superexchange-coupled dinuclear dysprosium(III) complex. J. Am. Chem. Soc. 2011, 133, 5319–5328. [Google Scholar] [CrossRef] [PubMed]
- Katoh, K.; Asano, R.; Miura, A.; Horii, Y.; Morita, T.; Breedlove, B.K.; Yamashita, M. Effect of f-f interactions on quantum tunnelling of the magnetization: Mono- and dinuclear Dy(III) phthalocyaninato triple-decker single-molecule magnets with the same octacoordination environment. Dalton Trans. 2014, 43, 7716–7725. [Google Scholar] [CrossRef] [PubMed]
- Xue, S.; Guo, Y.-N.; Ungur, L.; Tang, J.; Chibotaru, L.F. Tuning the magnetic interactions and relaxation dynamics of Dy2 single-molecule magnets. Chem. Eur. J. 2015, 21, 14099–14106. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Fang, M.; Evans, W.J.; Long, J.R. Strong exchange and magnetic blocking in N23−-radical-bridged lanthanide complexes. Nat. Chem. 2011, 3, 538–542. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Sangregorio, C.; Sessoli, R.; Gatteschi, D. Molecular engineering for single-chain-magnet behavior in a one-dimensional dysprosium–nitronyl nitroxide compound. Angew. Chem. Int. Edit. 2005, 44, 5817–5821. [Google Scholar] [CrossRef] [PubMed]
- Bernot, K.; Bogani, L.; Caneschi, A.; Gatteschi, D.; Sessoli, R. A family of rare-earth-based single chain magnets: Playing with anisotropy. J. Am. Chem. Soc. 2006, 128, 7947–7956. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, X.-L.; Wang, T.-W.; Song, Y.; You, X.-Z. Slow relaxation processes and single-ion magnetic behaviors in dysprosium-containing complexes. Inorg. Chem. 2010, 49, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Li, B.; Zhang, X.; Li, X.; Li, X.; Zhang, J. Three novel 1D lanthanide-carboxylate polymeric complexes: Syntheses, crystal structures and magnetic analyses. Dalton Trans. 2013, 42, 8504–8511. [Google Scholar] [CrossRef] [PubMed]
- Bartolome, E.; Bartolome, J.; Melnic, S.; Prodius, D.; Shova, S.; Arauzo, A.; Luzon, J.; Luis, F.; Turta, C. {Dy(α-fur)3}n: From double relaxation single-ion magnet behavior to 3D ordering. Dalton Trans. 2013, 42, 10153–10171. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Le Natur, F.; Cador, O.; Pointillart, F.; Calvez, G.; Daiguebonne, C.; Guillou, O.; Guizouarn, T.; Le Guennic, B.; Bernot, K. Experimental and theoretical evidence that electrostatics governs easy-axis orientation in Dy(III)-based molecular chains. Chem. Commun. 2014, 50, 13346–13348. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Meng, Y.-S.; Zhang, Y.-Q.; Jiang, S.-D.; Sun, H.-L.; Gao, S. A 1D dysprosium chain with slow magnetic relaxation constructed from a pyridine-N-oxide ligand. Chem. Commun. 2014, 50, 10434–10437. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.-C.; Zhang, M.; Wu, D.; Shao, D.; Zhao, X.-H.; Huang, W.; Wang, X.-Y. Single molecule magnet behavior observed in a 1-D dysprosium chain with quasi-D5h symmetry. Dalton Trans. 2015, 44, 20834–20838. [Google Scholar] [CrossRef] [PubMed]
- Holmberg, R.J.; Ho, L.T.A.; Ungur, L.; Korobkov, I.; Chibotaru, L.F.; Murugesu, M. Observation of unusual slow-relaxation of the magnetisation in a Gd-EDTA chelate. Dalton Trans. 2015, 44, 20321–20325. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Leng, J.-D.; Ding, Y.-S.; Wang, Y.; Zheng, Z.; Zheng, Y.-Z. Field and dilution effects on the magnetic relaxation behaviours of a 1D dysprosium(III)-carboxylate chain built from chiral ligands. Dalton Trans. 2015, 44, 13480–13484. [Google Scholar] [CrossRef] [PubMed]
- Holmberg, R.J.; Korobkov, I.; Murugesu, M. Enchaining EDTA-chelated lanthanide molecular magnets into ordered 1D networks. RSC Adv. 2016, 6, 72510–72518. [Google Scholar] [CrossRef]
- Khalfaoui, O.; Beghidja, A.; Long, J.; Boussadia, A.; Beghidja, C.; Guari, Y.; Larionova, J. Cinnamic acid derivatives rare-earth dinuclear complexes and one-dimensionnal architectures: Synthesis, characterization and magnetic properties. Dalton Trans. 2017, 46, 3943–3952. [Google Scholar] [CrossRef] [PubMed]
- Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The rich stereochemistry of eight-vertex polyhedra: A continuous shape measures study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Atanasov, M.; Bryan, A.M.; Lin, C.-Y.; Rekken, B.D.; Power, P.P.; Neese, F.; Long, J.R. Slow magnetization dynamics in a series of two-coordinate iron(II) complexes. Chem. Sci. 2013, 4, 125–138. [Google Scholar] [CrossRef]
- Meihaus, K.R.; Minasian, S.G.; Lukens, W.W.; Kozimor, S.A.; Shuh, D.K.; Tyliszczak, T.; Long, J.R. Influence of pyrazolate vs N-heterocyclic carbene ligands on the slow magnetic relaxation of homoleptic trischelate lanthanide(III) and uranium(III) complexes. J. Am. Chem. Soc. 2014, 136, 6056–6068. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, K.N. Theory of spin–lattice relaxation. Phys. Status Solidi (b) 1983, 117, 437–458. [Google Scholar] [CrossRef]
- Scott, P.L.; Jeffries, C.D. Spin-lattice relaxation in some rare-earth salts at helium temperatures; observation of the phonon bottleneck. Phys. Rev. 1962, 127, 32–51. [Google Scholar] [CrossRef]
- Amjad, A.; Figuerola, A.; Caneschi, A.; Sorace, L. Multiple magnetization reversal channels observed in a 3d-4f single molecule magnet. Magnetochemistry 2016, 2, 27. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Chilton, N.F.; Collison, D.; McInnes, E.J.L.; Winpenny, R.E.P.; Soncini, A. An electrostatic model for the determination of magnetic anisotropy in dysprosium complexes. Nat. Commun. 2013, 4, 2551. [Google Scholar] [CrossRef] [PubMed]
- APEX3 and SAINT, Version 3; Bruker AXS, Inc.: Madison, WI, USA, 2016.
- SADABS, Version 2.03; Bruker AXS, Inc.: Madison, WI, USA, 2001.
- Sheldrick, G. Crystal structure refinement with SHELXL. Acta Cryst. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Dowty, E. Atoms; Shape Software: Kingsport, TN, USA, 1999. [Google Scholar]
- Macrae, C.F.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Shields, G.P.; Taylor, R.; Towler, M.; van de Streek, J. Mercury: Visualization and analysis of crystal structures. J. Appl. Cryst. 2006, 39, 453–457. [Google Scholar] [CrossRef]
- Spek, A. Structure validation in chemical crystallography. Acta Cryst. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed]




| Compound | Dimensionality | τ at 1.8 K (ms) | Δ (cm−1) | m | C (s−1·K−m) | A(s−1·K−1) |
|---|---|---|---|---|---|---|
| [Dy(L)3(DMSO)(H2O)]2 (1) | dinuclear complex | 6.84 | 10 ± 1 | 9 * | 0.0078 ± 0.0003 | 79 ± 15 |
| [Dy(L′)3(DMSO)(H2O)]2 | dinuclear complex | 0.67 | - | 9 * | 0.38 ± 0.02 | 983 ± 36 |
| [Dy2(L)6(DMSO)(H2O)]n·DMF | 1-D structure | 2.04 | - | 4.5 ± 0.2 | 3.6 ± 0.8 | 249 ± 12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalfaoui, O.; Beghidja, A.; Long, J.; Beghidja, C.; Guari, Y.; Larionova, J. Field-Induced Slow Relaxation in a Dinuclear Dysprosium(III) Complex Based on 3-Methoxycinnamic Acid. Inorganics 2018, 6, 35. https://doi.org/10.3390/inorganics6010035
Khalfaoui O, Beghidja A, Long J, Beghidja C, Guari Y, Larionova J. Field-Induced Slow Relaxation in a Dinuclear Dysprosium(III) Complex Based on 3-Methoxycinnamic Acid. Inorganics. 2018; 6(1):35. https://doi.org/10.3390/inorganics6010035
Chicago/Turabian StyleKhalfaoui, Ouafa, Adel Beghidja, Jérôme Long, Chahrazed Beghidja, Yannick Guari, and Joulia Larionova. 2018. "Field-Induced Slow Relaxation in a Dinuclear Dysprosium(III) Complex Based on 3-Methoxycinnamic Acid" Inorganics 6, no. 1: 35. https://doi.org/10.3390/inorganics6010035
APA StyleKhalfaoui, O., Beghidja, A., Long, J., Beghidja, C., Guari, Y., & Larionova, J. (2018). Field-Induced Slow Relaxation in a Dinuclear Dysprosium(III) Complex Based on 3-Methoxycinnamic Acid. Inorganics, 6(1), 35. https://doi.org/10.3390/inorganics6010035