Local and Average Structure of Yb-Doped Ceria through Synchrotron and Neutron Pair Distribution Function
Abstract
:1. Introduction
2. Results and Discussion
2.1. Long-Range Structure
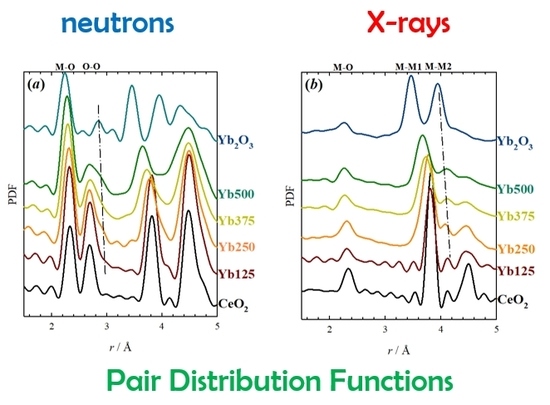
2.2. Local Structure—Neutron
2.3. Local Structure—X-Ray
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kilner, J.A. Defects and conductivity in ceria-based oxides. Chem. Lett. 2008, 37, 1012–1015. [Google Scholar] [CrossRef]
- Mogensen, M.; Sammes, N.M.; Tompsett, G.A. Physical, chemical and electrochemical properties of pure and doped ceria. Solid State Ionics 2000, 129, 63–94. [Google Scholar] [CrossRef]
- Coduri, M.; Checchia, S.; Longhi, M.; Ceresoli, D.; Scavini, M. Rare Earth Doped Ceria: The Complex Connection Between Structure and Properties. Front. Chem. 2018, 6, 526. [Google Scholar] [CrossRef]
- Malecka, M.A. Ceria-Based Mixed Oxides—Beautiful Structures. Chem. Select 2016, 1, 4246–4254. [Google Scholar] [CrossRef]
- Artini, C. Rare-Earth-Doped Ceria Systems and Their Performance as Solid Electrolytes: A Puzzling Tangle of Structural Issues at the Average and Local Scale. Inorg. Chem. 2018, 57, 13047–13062. [Google Scholar] [CrossRef] [Green Version]
- Horlait, D.; Claparede, L.; Clavier, N.; Szenknect, S.; Dacheux, N.; Ravaux, J.; Podor, R. Stability and Structural Evolution of CeIV1−xLnIIIxO2−x/2 Solid Solutions: A coupled µ-raman/XRD approach. Inorg. Chem. 2011, 50, 7150–7161. [Google Scholar] [CrossRef]
- Balazs, G.B.; Glass, R.S. ac impedance studies of rare earth oxide doped ceria. Solid State Ionics 1995, 76, 155–162. [Google Scholar] [CrossRef]
- Faber, J.; Geoffroy, C.; Roux, A.; Sylvestre, A.; Abelard, P. A Systematic Investigation of the dc Electrical Conductivity of Rare-Earth Doped Ceria. Appl. Phys. A 1989, 49, 225–232. [Google Scholar] [CrossRef]
- Andersson, D.A.; Simak, S.I.; Skorodumova, N.V.; Abrikosov, I.A.; Johansson, B. Optimization of ionic conductivity in doped ceria. Proc. Natl. Acad. Sci. USA 2006, 103, 3518–3521. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, H.; Deguchi, H.; Miura, K.; Horiuchi, M.; Inagaki, T. Investigation of the relationship between the ionic conductivity and the local structures of singly and doubly doped ceria compounds using EXAFS measurement. Solid State Ionics 2001, 140, 191–199. [Google Scholar] [CrossRef]
- Nitani, H.; Nakagawa, T.; Yamanouchi, M.; Osuki, T.; Yuya, M.; Yamamoto, T.A. XAFS and XRD study of ceria doped with Pr, Nd or Sm. Mater. Lett. 2004, 58, 2076–2081. [Google Scholar] [CrossRef]
- Shirbhate, S.C.; Yadav, A.K.; Acharya, S.A. Extended x-ray absorption fine structure spectroscopy and x-ray absorption near edge spectroscopy study of aliovalent doped ceria to correlate local structural changes with oxygen vacancies clustering. Appl. Phys. Lett. 2016, 108, 143501. [Google Scholar] [CrossRef]
- Giannici, F.; Gregori, G.; Aliotta, C.; Longo, A.; Maier, J.; Martorana, A. Structure and oxide-ion conductivity: Local order, defect interactions and grain boundary effects in acceptor-doped ceria. Chem. Mater. 2014, 26, 5594–6006. [Google Scholar] [CrossRef]
- Hooper, J.; Ismail, A.; Giorgi, J.B.; Woo, T.K. Computational insights into the nature of increased ionic conductivity in concentrated samarium-doped ceria: A genetic algorithm study. Phys. Chem. Chem. Phys. 2010, 12, 12969–12972. [Google Scholar] [CrossRef]
- Deguchi, H.; Yoshida, H.; Inagaki, T.; Horiuchi, M. Study of doped ceria using multiple data set fit. Solid State Ionics 2005, 176, 1817–1825. [Google Scholar] [CrossRef]
- Coduri, M.; Scavini, M.; Brunelli, M.; Pedrazzin, E.; Masala, P. Structural characterization of Tb- and Pr-doped ceria. Solid State Ionics 2014, 268, 150–155. [Google Scholar] [CrossRef]
- Martinez-Arias, A.; Hungria, A.B.; Fernandez-Garcia, M.; Iglesias-Juez, A.; Conesa, J.C.; Mather, G.C.; Munuera, G. Cerium-terbium mixed oxides as potential materials for anodes in solid oxide fuel cells. J. Power Sources 2005, 151, 43–51. [Google Scholar] [CrossRef]
- Coduri, M.; Brunelli, M.; Scavini, M.; Allieta, M.; Masala, P.; Capogna, L.; Fischer, H.; Ferrero, C. Rare Earth doped ceria: A combined X-ray and neutron pair distribution function study. Z. Kristallogr. 2012, 227, 272–279. [Google Scholar] [CrossRef]
- Andrievskaya, E.R.; Kornienko, O.A.; Sameljuk, A.V.; Sayir, A. Phase relation studies in the CeO2–La2O3 system at 1100–1500 °C. J. Eur. Ceram. Soc. 2011, 31, 1277–1283. [Google Scholar] [CrossRef]
- Wilkes, M.F.; Hayden, P.; Bhattacharya, A.K. Catalytic studies on ceria lanthana solid solutions III. Surface segregation and solid state studies. J. Catal. 2003, 219, 305–309. [Google Scholar] [CrossRef]
- Mandal, B.P.; Grover, V.; Roy, M.; Tyagi, A.K. X-ray diffraction and raman spectroscopic investigation on the phase relations in Yb2O3- and Tm2O3-Substituted CeO2. J. Am. Ceram. Soc. 2007, 90, 2961–2965. [Google Scholar] [CrossRef]
- Coduri, M.; Scavini, M.; Pani, M.; Carnasciali, M.M.; Klein, H.; Artini, C. From nano to microcrystals: Effects of different synthetic pathways on the defect architecture in heavily Gd-doped ceria. Phys. Chem. Chem. Phys. 2017, 19, 11612–11630. [Google Scholar] [CrossRef]
- Coduri, M.; Scavini, M.; Allieta, M.; Brunelli, M.; Ferrero, C. Defect structure of Y-doped ceria on different length scales. Chem. Mater. 2013, 25, 4278–4289. [Google Scholar] [CrossRef]
- Scavini, M.; Coduri, M.; Allieta, M.; Masala, P.; Cappelli, S.; Oliva, C.; Brunelli, M.; Orsini, F.; Ferrero, C. Percolating hierarchical defect structures drive phase transformation in Ce1−xGdxO2−x/2: A total scattering study. IUCr J. 2015, 2, 511–522. [Google Scholar] [CrossRef]
- Coduri, M.; Masala, P.; Allieta, M.; Peral, I.; Brunelli, M.; Biffi, C.A.; Scavini, M. Phase Transformations in the CeO2–Sm2O3 System: A multiscale powder diffraction investigation. Inorg. Chem. 2018, 57, 879–891. [Google Scholar] [CrossRef]
- Artini, C.; Carnasciali, M.M.; Plaisier, J.R.; Costa, G.A.; Pani, M. A novel method for the evaluation of the Rare Earth (RE) coordination number in RE-doped ceria through Raman spectroscopy. Solid State Ionics 2017, 311, 90–97. [Google Scholar] [CrossRef]
- Ou, D.R.; Mori, T.; Ye, F.; Takahashi, M. Oxygen vacancy ordering in heavily rare-earth-doped ceria. Appl. Phys. Lett. 2006, 89, 171911. [Google Scholar] [CrossRef] [Green Version]
- Ou, D.R.; Mori, T.; Ye, F.; Zou, J.; Auchterlonie, G.; Drennan, J. Oxygen-vacancy ordering in lanthanide-doped ceria: Dopant type dependence and structure model. Phys. Rev. B 2008, 77, 240108. [Google Scholar] [CrossRef]
- Ye, F.; Mori, T.; Ou, D.R.; Zou, J.; Drennan, J. A structure model of nano-sized domain in Gd-doped ceria. Solid State Ionics 2009, 180, 1414–1420. [Google Scholar] [CrossRef]
- Grover, V.; Banerji, A.; Sengupta, P.; Tyagi, A.K. Raman, XRD and microscopic investigations on CeO2– Lu2O3 and CeO2–Sc2O3 systems: A sub-solidus phase evolution study. J. Solid State Chem. 2008, 181, 1930–1935. [Google Scholar] [CrossRef]
- Malecka, M.A.; Kepinski, L.; Maczka, M. Structure and phase composition of nanocrystalline Ce1−xLuxO2−y. J. Solid State Chem. 2008, 18, 2306–2312. [Google Scholar] [CrossRef]
- Artini, C.; Pani, M.; Carnasciali, M.M.; Plaisier, J.R.; Costa, G.A. Lu-, Sm-, and Gd-doped Ceria: A comparative approach to their structural properties. Inorg. Chem. 2016, 55, 10567–10579. [Google Scholar] [CrossRef]
- Neutron News. 1992. Available online: https://www.ncnr.nist.gov/resources/n-lengths/ (accessed on 6 June 2016).
- Argyriou, D.N. Measurement of the static disorder contribution to the temperature factor in cubic stabilized ZrO2. J. Appl. Crystallogr. 1994, 27, 155–158. [Google Scholar] [CrossRef]
- Coduri, M.; Scavini, M.; Allieta, M.; Brunelli, M.; Ferrero, C. Local disorder in yttrium doped ceria (Ce1−xYxO2−x/2) probed by joint X-ray and Neutron Powder Diffraction. J. Phys. Conf. Ser. 2012, 340, 012056. [Google Scholar] [CrossRef]
- Ohashi, T.; Yamazaki, S.; Tokunaga, T.; Arita, Y.; Matsui, T.; Harami, T.; Kobayashi, K. EXAFS study of Ce1−xGdxO2−x/2. Solid State Ionics 1998, 113–115, 559–564. [Google Scholar] [CrossRef]
- Neder, N.B.; Frey, F.; Schulz, H. Defect structure of Zirconia (Zr0.85Ca0.15O1.85) at 290 K and 1550 K. Acta Cryst. 1990, 46, 799–809. [Google Scholar] [CrossRef]
- Allieta, M.; Brunelli, M.; Coduri, M.; Scavini, M.; Ferrero, C. Differential Pair Distribution Function applied to Ce1−xGdxO2−x/2 system. Z. Krist. Proc. 2011, 1, 15–20. [Google Scholar] [CrossRef]
- Scavini, M.; Coduri, M.; Allieta, M.; Brunelli, M.; Ferrero, C. Probing complex disorder in Ce1−xGdxO2−x/2 using the pair distribution function analysis. Chem. Mater. 2012, 24, 1338–1345. [Google Scholar] [CrossRef]
- Sardar, K.; Playford, H.Y.; Darton, R.J.; Barney, E.R.; Hannon, A.C.; Tompsett, D.; Fisher, J.; Kashtiban, R.J.; Sloan, J.; Ramos, S.; et al. Nanocrystalline cerium-bismuth oxides: Synthesis, structural characterization, and redox properties. Chem. Mater. 2010, 22, 6191–6201. [Google Scholar] [CrossRef]
- Gateshki, M.; Niederberger, M.; Deshpande, A.S.; Ren, Y.; and Petkov, V. Atomic-scale structure of nanocrystalline CeO2–ZrO2 oxides by total x-ray diffraction and pair distribution function analysis. J. Phys. Condens. Matter. 2007, 19, 156205. [Google Scholar] [CrossRef]
- Coduri, M.; Scavini, M.; Brunelli, M.; Masala, P. In situ pair distribution function study on lanthanum doped ceria. Phys. Chem. Chem. Phys. 2013, 15, 8495–8505. [Google Scholar] [CrossRef]
- Kraynis, O.; Timoshenko, J.; Huang, J.; Singh, H.; Wachtel, E.; Frenkel, A.I.; Lubomirsky, I. Modeling Strain Distribution at the Atomic Level in Doped Ceria Films with Extended X-ray Absorption Fine Structure Specroscopy. Inorg. Chem. 2019, 58, 7527–7536. [Google Scholar] [CrossRef]
- Checchia, S.; Scavini, M.; Allieta, M.; Brunelli, M.; Ferrero, C.; Coduri, M. Size and spatial correlation of defective domains in yttrium doped CeO2. Powder Diffr. 2015, 30, S119–S126. [Google Scholar] [CrossRef]
- Oliva, C.; Orsini, F.; Cappelli, S.; Arosio, P.; Allieta, M.; Coduri, M.; Scavini, M. Electron Spin Resonance and Atomic Force Microscopy Study on Gadolinium Doped Ceria. J. Spectrosc. 2015, 2015, 491840. [Google Scholar] [CrossRef]
- Scavini, M.; Brunelli, M.; Cazzaniga, M.; Checchia, S.; Coduri, M.; Cuello, G.J.; Ferrero, C.; Giannuzzi, M. Neutron Diffraction Study of Local and Mesoscopic Disorder Induced by La and Yb Double Doping in Ce1−x−yLaxYbyO2−(x+y)/2, Using PDF Analysis; Institute Laue Langevin (ILL): Grenoble, France, 2015. [Google Scholar]
- Fischer, H.E.; Cuello, G.J.; Palleau, P.; Feltin, D.; Barnes, A.C.; Badyal, Y.S.; Simonson, J.M. D4c: A very high precision diffractometer for disordered materials. Appl. Phys. A 2002, 74, S160–S162. [Google Scholar] [CrossRef]
- Larson, A.C.; Von Dreele, R.B. General Structural Analysis System (GSAS); Los Alamos National Laboratory: Santa Fe, NM, USA, 2004; pp. 86–748. [Google Scholar]
- Qiu, X.; Thompson, J.W.; Billinge, S.L.J. PDFgetX2: A GUI driven program to obtain the pair distribution function from X-ray powder diffraction data. J. Appl. Crystallogr. 2004, 37, 678. [Google Scholar] [CrossRef]
- Farrow, C.L.; Juhás, P.; Liu, J.W.; Bryndin, D.; Božin, E.S.; Bloch, J.; Proffen, T.; Billinge, S.J.L. PDFfit2 and PDFgui: Computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter. 2007, 19, 335219. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]








| μ (≤ 0.250) | 0 | 0.125 | 0.250 |
| space group | Fm-3m | Fm-3m | Fm-3m |
| a/Å | 5.40475(3) | 5.39803(3) | 5.38427(5) |
| msd(M)/Å2 | 0.00135(3) | 0.0043(7) | 0.0083(3) |
| msd(O)/Å2 | 0.00368(1) | 0.0067(8) | 0.0113(8) |
| msd mean/Å2 | 0.00138(9) | 0.00442(1) | 0.00836(0) |
| R(F2) | 0.0242 | 0.0173 | 0.0301 |
| RP | 0.0553 | 0.0288 | 0.0264 |
| ε/Δd/d | 0.000062(8) | 0.00041(2) | 0.00129(5) |
| DV/nm | 247(10) | 92(4) | 123(15) |
| μ(>0.250) | 0.375 | 0.500 | 1 |
| space group | Ia-3 | Ia-3 | Ia-3 |
| a/Å | 10.73049(1) | 10.68752(0) | 10.42843(7) |
| x(M2) | −0.0037(9) | −0.0125(4) | −0.03241(2) |
| x(O1) | 0.37729(4) | 0.37729(4) | 0.3910(3) |
| y(O1) | 0.14326(6) | 0.14326(6) | 0.1523(3) |
| z(O1) | 0.37775(3) | 0.37775(3) | 0.3809(3) |
| x(O2) | 0.37230(2) | 0.37230(2) | - |
| msd11(M1) | 0.014(7) | 0.024(1) | 0.00190(6) |
| msd12(M1) | 0.000(5) | 0.010(9) | - |
| msd11(M2) | 0.004(2) | 0.008(4) | 0.00150(4) |
| msd22(M2) | 0.017(4) | 0.004(4) | ≡msd11(M2) |
| msd33(M2) | 0.017(9) | 0.026(3) | ≡msd11(M2) |
| msd23(M2) | −0.004(2) | −0.006(4) | - |
| msd(O1/O2) | 0.006(1) | 0.014(7) | 0.0023(5) |
| Uave | 0.0134(6) | 0.0148(1) | 0.00160(2) |
| R(F2) | 0.0392 | 0.0323 | 0.0147 |
| RP | 0.0242 | 0.0292 | 0.0392 |
| ε/Δd/d | 0.00202(7) | 0.0031(2) | - |
| DV/nm | 67(7) | 77(17) | - |
| μ | Neutron | X-ray | |||||
|---|---|---|---|---|---|---|---|
| M–O Distance (Å) | O–O1 Distance (Å) | O–O2 Distance (Å) | O–O Relative Intensity | M–M1 Distance (Å) | M–M2 Distance (Å) | M–M Relative Intensity | |
| 0 | 2.341 | 2.702 | - | - | 3.826 | - | - |
| 0.125 | 2.323 | 2.697 | 2.875 | 0.098 | 3.807 | 4.122 | 0.047 |
| 0.250 | 2.306 | 2.683 | 2.870 | 0.231 | 3.783 | 4.081 | 0.141 |
| 0.375 | 2.296 | 2.687 | 2.865 | 0.272 | 3.728 | 4.101 | 0.171 |
| 0.500 | 2.284 | 2.669 | 2.864 | 0.378 | 3.675 | 4.090 | 0.290 |
| 1 | 2.233 | - | 2.851 | - | 3.472 | 3.936 | 0.493 |
| Model | Yb125 | Yb250 | ||
|---|---|---|---|---|
| Fluorite | Cluster | Fluorite | Cluster | |
| a | 10.766(5) | 10.770(5) | 10.724(6) | 10.747(7) |
| msd(M) | 0.0064(7) | 0.0060(8) | 0.0105(10) | 0.0073(10) |
| msd(O) | 0.0056(7) | 0.0056(8) | 0.0142(14) | 0.0136(15) |
| O shift/Å | 0 | 0.178 | 0 | 0.185 |
| Rw | 0.091 | 0.069 | 0.177 | 0.103 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coduri, M.; Bozzetti, D.; Checchia, S.; Brunelli, M.; Scavini, M. Local and Average Structure of Yb-Doped Ceria through Synchrotron and Neutron Pair Distribution Function. Inorganics 2019, 7, 102. https://doi.org/10.3390/inorganics7080102
Coduri M, Bozzetti D, Checchia S, Brunelli M, Scavini M. Local and Average Structure of Yb-Doped Ceria through Synchrotron and Neutron Pair Distribution Function. Inorganics. 2019; 7(8):102. https://doi.org/10.3390/inorganics7080102
Chicago/Turabian StyleCoduri, Mauro, Dario Bozzetti, Stefano Checchia, Michela Brunelli, and Marco Scavini. 2019. "Local and Average Structure of Yb-Doped Ceria through Synchrotron and Neutron Pair Distribution Function" Inorganics 7, no. 8: 102. https://doi.org/10.3390/inorganics7080102
APA StyleCoduri, M., Bozzetti, D., Checchia, S., Brunelli, M., & Scavini, M. (2019). Local and Average Structure of Yb-Doped Ceria through Synchrotron and Neutron Pair Distribution Function. Inorganics, 7(8), 102. https://doi.org/10.3390/inorganics7080102