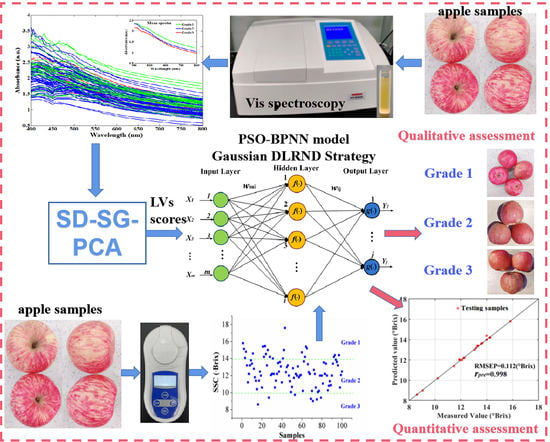
Qualitative and Quantitative Assessments of Apple Quality Using Vis Spectroscopy Combined with Improved Particle-Swarm-Optimized Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. SSC Measurement
2.3. Statistical Analysis
2.4. Spectral Acquisition
2.5. Spectral Pretreatment
2.6. Spectral Features Extraction
2.7. Qualitative and Quantitative Assessments Modeling
2.8. Dynamic Learning Rate Decay Strategy of BPNN Modeling
2.9. Particle Swarm Optimization (PSO)-Optimized BPNN Algorithm
3. Results and Analysis
3.1. Statistical Analysis of SSC
3.2. Spectral Acquisition
3.3. Spectral Pretreatment
3.4. Spectral Features Extraction
3.5. SSC Classification Assessments Based on BPNN Models
3.6. SD-SG-PCA-BPNN Model Combined with DLRND Strategy
3.7. SSC Classification Based on PSO-Optimized SD-SG-PCA-BPNN Algorithm
3.8. Quantitative Assessment of Apple SSC
4. Discussion
4.1. Quality Assessments of Fruits Based on Spectroscopy Technique
4.2. Comparison of Qualitative Assessments between Different Algorithms
4.3. Comparison of Quantitative Assessments between Different Algorithms
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jaeger, S.R.; Antúnez, L.; Ares, G.; Swaney-Stueve, M.; Jin, D.; Harker, F.R. Quality perceptions regarding external appearance of apples: Insights from experts and consumers in four countries. Postharvest Biol. Technol. 2018, 146, 99–107. [Google Scholar] [CrossRef]
- Zheng, Q.; Song, J.; Doncaster, K.; Rowland, E.; Byers, D.M. Qualitative and quantitative evaluation of protein extraction protocols for apple and strawberry fruit suitable for two-dimensional electrophoresis and mass spectrometry analysis. J. Agric. Food Chem. 2007, 55, 1663–1673. [Google Scholar] [CrossRef] [PubMed]
- Lorente, D.; Escandell-Montero, P.; Cubero, S.; Gomez-Sanchis, J.; Blasco, J. Visible–NIR reflectance spectroscopy and manifold learning methods applied to the detection of fungal infections on citrus fruit. J. Food Eng. 2015, 163, 17–24. [Google Scholar] [CrossRef]
- Mo, C.; Kim, M.S.; Kim, G.; Lim, J.; Delwiche, S.R.; Chao, K.; Lee, H.; Cho, B.-K. Spatial assessment of soluble solid contents on apple slices using hyperspectral imaging. Biosyst. Eng. 2017, 159, 10–21. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Y.; Sun, Y.; Zhou, H.; Chen, K. Identification of apple varieties using a multichannel hyperspectral imaging system. Sensors 2020, 20, 5120. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wu, Y.; Li, L.; Li, L. Nondestructive detection for forecasting the level of acidity and sweetness of apple based on NIR spectroscopy. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25 March 2017. [Google Scholar]
- Eisenstecken, D.; Sturz, B.; Robatscher, P.; Lozano, L.; Zanella, A.; Oberhuber, M. The potential of near infrared spectroscopy (NIRS) to trace apple origin: Study on different cultivars and orchard elevations. Postharvest Biol. Technol. 2019, 147, 123–131. [Google Scholar] [CrossRef]
- Mendoza, F.; Lu, R.; Cen, H. Grading of apples based on firmness and soluble solids content using Vis/SWNIR spectroscopy and spectral scattering techniques. J. Food Eng. 2014, 125, 59–68. [Google Scholar] [CrossRef]
- Song, W.; Wang, H.; Maguire, P.; Nibouche, O. Differentiation of organic and non-organic apples using near infrared reflectance spectroscopy-a pattern recognition approach. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Tran, N.-T.; Phan, Q.-T.; Nguyen, C.-N.; Fukuzawa, M. Machine learning-based classification of apple sweetness with multispectral sensor. In Proceedings of the 2021 21st ACIS International Winter Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD-Winter), Ho Chi Minh City, Vietnam, 28–30 January 2021; pp. 23–27. [Google Scholar]
- Zhang, M.; Zhang, B.; Li, H.; Shen, M.; Zhang, H.; Zhao, J. Non-Destructive detection of apple maturity by constructing spectral index based on reflectance spectrum. In Proceedings of the 2020 ASABE Annual International Virtual Meeting, Online, 13–15 July 2020. [Google Scholar]
- Xu, S.; Lu, H.; Wang, X.; Ference, C.M.; Liang, X.; Qiu, G. Nondestructive detection of internal flavor in ‘Shatian’ pomelo fruit based on visible/near infrared spectroscopy. HortScience 2021, 56, 1325–1330. [Google Scholar] [CrossRef]
- Hua, S.H.; Hsu, H.C.; Han, P. P-wave visible–shortwave–near-infrared (Vis-SW-NIR) detection system for the prediction of soluble solids content and firmness on wax apples. Appl. Spectrosc. 2019, 73, 1135–1145. [Google Scholar] [CrossRef]
- Fan, S.; Guo, Z.; Zhang, B.; Huang, W.; Zhao, C. Using Vis/NIR diffuse transmittance spectroscopy and multivariate analysis to predicate soluble solids content of apple. Food Anal. Methods 2016, 9, 1333–1343. [Google Scholar] [CrossRef]
- Torres, E.; Recasens, I.; Alegre, S. Potential of VIS/NIR spectroscopy to detect and predict bitter pit in ‘golden smoothee’ apples. Span. J. Agric. Res. 2021, 19, e1001. [Google Scholar] [CrossRef]
- Scalisi, A.; O’Connell, M.G. Application of visible/NIR spectroscopy for the estimation of soluble solids, dry matter and flesh firmness in stone fruits. J. Sci. Food Agric. 2021, 101, 2100–2107. [Google Scholar] [CrossRef]
- Tang, C.X.; He, H.Y.; Li, E.B.; Li, H.Q. Multispectral imaging for predicting sugar content of ‘Fuji’ apples. Opt. Laser Technol. 2018, 106, 280–285. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Opeña, H.; Yusiong, J.P. Automated tomato maturity grading using ABC-trained artificial neural networks. Malays. J. Comput. Sci. 2017, 30, 12–26. [Google Scholar] [CrossRef]
- Wei, K.; Ma, C.; Sun, K.; Liu, Q.; Pan, L. Relationship between optical properties and soluble sugar contents of apple flesh during storage. Postharvest Biol. Technol. 2020, 159, 111021. [Google Scholar] [CrossRef]
- Issa, M.M.; Nejem, R.M.; Van Staden, R.I.S.; Aboul-Enein, H.Y. New approach application of data transformation in mean centering of ratio spectra method. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2015, 142, 204–209. [Google Scholar] [CrossRef]
- Ji, W.; Viscarra Rossel, R.A.; Shi, Z. Improved estimates of organic carbon using proximally sensed Vis–NIR spectra corrected by piecewise direct standardization. Eur. J. Soil Sci. 2015, 66, 670–678. [Google Scholar] [CrossRef]
- Moura-Bueno, J.; Dalmolin, R.; Caten, A.; Dotto, A.; Demattê, J.A. Stratification of a local VIS-NIR-SWIR spectral library by homogeneity criteria yields more accurate soil organic carbon predictions. Geoderma. 2019, 337, 565–581. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z.; Tian, X.; Yang, X.; Cai, Z.; Li, J. Online analysis of watercore apples by considering different speeds and orientations based on Vis/NIR full-transmittance spectroscopy. Infrared Phys. Technol. 2022, 122, 104090. [Google Scholar] [CrossRef]
- Nan, W.U.; Liu, J.A.; Zhou, G.Y.; Yan, R.K. Prediction of chlorophyll content of leaves of oil camelliae after being infected with anthracnose based on vis/nir spectroscopy. Spectrosc. Spect. Anal. 2012, 32, 1221. [Google Scholar]
- Feng, L.; Chen, X.Q.; Cheng, Z.S.; Wen, X.D. Quantitative analysis for adsorption of polycarboxylate superplaticizer with different side-chain length on tuff powder using second derivative spectrometry. Spectrosc. Spect. Anal. 2019, 39, 2788–2793. [Google Scholar]
- Zhang, L.; Zhang, B.; Zhou, J.; Gu, B.; Tian, G. Uninformative biological variability elimination in apple soluble solids content inspection by using fourier transform near-infrared spectroscopy combined with multivariate analysis and wavelength selection algorithm. J. Anal. Methods Chem. 2017, 2017, 2525147. [Google Scholar] [CrossRef] [PubMed]
- Dhanoa, M.S.; Lister, S.J.; Sanderson, R.; Barnes, R.J. The link between multiplicative scatter correction (MSC) and standard normal variate (SNV) transformations of NIR spectra. J. Near Infrared Spectrosc. 1994, 2, 43–47. [Google Scholar] [CrossRef]
- Zhu, C.; Song, X.-S.; Liu, H.-B.; Chen, G.-Q.; Zhu, T. Optimize classification testing of apple juice combining derivative fluorescence spectroscopy with PCA. Int. J. Mod. Phys. B 2022, 36, 2240021. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Wang, W.; Zhang, J. Estimation of apple storage quality properties based on the mechanical properties with bp neural network. Trans. CSAE 2007, 23, 150–153. [Google Scholar]
- He, Y.; Li, X.-L.; Shao, Y.-N. Discrimination of varieties of apple using near infrared spectra based on principal component analysis and artificial neural network model. Spectrosc. Spectr. Anal. 2006, 26, 850–853. [Google Scholar]
- Sun, J.; Wu, X.; Palade, V.; Fang, W.; Lai, C.-H.; Xu, W. Convergence analysis and improvements of quantum-behaved particle swarm optimization. Inf. Sci. 2012, 193, 81–103. [Google Scholar] [CrossRef]
- Wang, S.J.; Dai, Y.T.; Shen, J.H.; Xuan, J.X. Research on expansion and classifcation of imbalanced data based on SMOTE algorithm. Sci. Rep. 2021, 11, 24039. [Google Scholar] [CrossRef]
- Mohd Naeem, M.N.; Mohd Fairulnizal, M.N.; Norhayati, M.K.; Zaiton, A.; Norliza, A.H.; Wan Syuriahti, W.Z.; Mohd Azerulazree, J.; Aswir, A.R.; Rusidah, S. The nutritional composition of fruit jams in the malaysian market. J. Saudi Soc. Agric. Sci. 2017, 16, 89–96. [Google Scholar] [CrossRef]
- Nam, Y.W.; Arai, Y.; Kunizane, T.; Koizumi, A. Water leak detection based on convolutional neural network (cnn) using actual leak sounds and the hold-out method. Water Supply 2021, 21, 3477–3485. [Google Scholar] [CrossRef]
- Behera, L.; Kumar, S.; Patnaik, A. On adaptive learning rate that guarantees convergence in feedforward networks. IEEE Trans. Neural Net. 2006, 17, 1116–1125. [Google Scholar] [CrossRef]
- Shen, W.; Li, G.; Wei, X.; Fu, Q.; Zhang, Y.; Qu, T.; Chen, C.; Wang, R. Assessment of dairy cow feed intake based on bp neural network with polynomial decay learning rate. Inf. Process. Agric. 2022, 9, 266–275. [Google Scholar] [CrossRef]
- Tollenaere, T. SuperSAB: Fast adaptive back propagation with good scaling properties. Neural Netw. 1990, 3, 561–573. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with warm restart. arxiv 2016, arXiv:1608.03983. [Google Scholar]
- Li, Y.; Zhang, Q.; Yoon, S.W. Gaussian process regression-based learning rate optimization in convolutional neural networks for medical images classification. Expert Syst. Appl. 2021, 184, 115357. [Google Scholar] [CrossRef]
- Fang, X.; Luo, H.; Tang, J. Structural damage detection using neural network with learning rate improvement. Comput. Struct. 2005, 83, 2150–2161. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Abd Elaziz, M. Review on applications of particle swarm optimization in solar energy systems. Int. J. Environ. Sci. Technol. 2019, 16, 1159–1170. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl. Based Syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Rose, H.E. Breakdown of the Lambert-Beer law. Nature 1952, 169, 287–288. [Google Scholar] [CrossRef]
- Alimohammadi, F.; Rasekh, M.; Sayyah, A.H.A.; Abbaspour-Gilandeh, Y.; Karami, H.; Sharabiani, V.R.; Fioravanti, A.; Gancarz, M.; Findura, P.; Kwaśniewski, D. Hyperspectral imaging coupled with multivariate analysis and artificial intelligence to the classification of maize kernels. Int. Agrophys. 2022, 36, 83–91. [Google Scholar] [CrossRef] [PubMed]
- Sharabiani, V.R.; Nazarloo, A.S.; Taghinezhad, E.; Veza, I.; Szumny, A.; Figiel, A. Prediction of winter wheat leaf chlorophyll content based on VIS/NIR spectroscopy using ANN and PLSR. Food Sci. Nutr. 2022, 11, 2166–2175. [Google Scholar] [CrossRef]
- Soltani Nazarloo, A.; Rasooli Sharabiani, V.; Abbaspour Gilandeh, Y.; Taghinezhad, E.; Szymanek, M.; Sprawka, M. Feasibility of using VIS/NIR spectroscopy and multivariate analysis for pesticide residue detection in tomatoes. Processes 2021, 9, 196. [Google Scholar] [CrossRef]
- Khorramifar, A.; Sharabiani, V.R.; Karami, H.; Kisalaei, A.; Lozano, J.; Rusinek, R.; Gancarz, M. Investigating changes in pH and soluble solids content of potato during the storage by electronic nose and Vis/NIR spectroscopy. Foods 2022, 11, 4077. [Google Scholar] [CrossRef]
- Escuredo, O.; Seijo-Rodríguez, A.; Inmaculada González-Martín, M.; Shantal Rodríguez-Flores, M.; Carmen Seijo, M. Potential of near infrared spectroscopy for predicting the physicochemical properties on potato flesh. Microchem. J. 2018, 141, 451–457. [Google Scholar] [CrossRef]
- Kohonen, T. Physiological interpretation of the self-organizing map algorithm. Neural Netw. 1993, 6, 895–905. [Google Scholar] [CrossRef]
- Albadr, M.A.A.; Tiun, S. Extreme learning machine: A review. Int. J. Appl. Eng. Res. 2017, 12, 4610–4623. [Google Scholar]
- Hajipour, A.; Shams-Nateri, A. Effect of classification by competitive neural network on reconstruction of reflectance spectra using principal component analysis. Color Res. Appl. 2017, 42, 182–188. [Google Scholar] [CrossRef]
- Zidan, M.; Abdel-Aty, A.-H.; El-shafei, M.; Feraig, M.; Al-Sbou, Y.; Eleuch, H.; Abdel-Aty, M. Quantum classification algorithm based on competitive learning neural network and entanglement measure. Appl. Sci. 2019, 9, 1277. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Luo, J.; Xu, Y.; Zhang, X. An enhanced bacterial foraging optimization and its application for training kernel extreme learning machine. Appl. Soft Comput. 2020, 86, 105884. [Google Scholar] [CrossRef]
- Kour, V.P.; Arora, S. Particle swarm optimization based support vector machine (P-SVM) for the segmentation and classification of plants. IEEE Access 2019, 7, 29374–29385. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, J.; Zhou, X.; Wu, X.; Lu, B.; Dai, C. Research on apple origin classification based on variable iterative space shrinkage approach with stepwise regression–support vector machine algorithm and visible-near infrared hyperspectral imaging. J. Food Process Eng. 2020, 43, e13432. [Google Scholar] [CrossRef]





















| Grade | SSC Range (°Brix) | Minimum (°Brix) | Maximum (°Brix) | Mean (°Brix) | Variance (°Brix) | SE of Mean * (°Brix) | MAD ** (°Brix) | CV *** (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 14–17.99 | 14.2 | 17.6 | 14.83 | 0.668 | 0.17423 | 0.5909 | 0.0551 |
| 2 | 10–13.99 | 10.2 | 13.867 | 12.06 | 1.136 | 0.12649 | 0.8512 | 0.0884 |
| 3 | 8–9.99 | 8.6 | 9.733 | 9.23 | 0.127 | 0.1348 | 0.2531 | 0.0386 |
| No. | Models | LVs | Neuron Number in Hidden Layer | Learning Rate | Classification Accuracy/% | Recall Rate/% | F1 Score/% |
|---|---|---|---|---|---|---|---|
| 1 | SNV-BPNN | 8 | 6 | 0.006 | 75.76 | 74.05 | 0.7675 |
| 2 | VN-BPNN | 5 | 10 | 0.004 | 66.67 | 63.55 | 0.6440 |
| 3 | SG-BPNN | 3 | 11 | 0.004 | 69.70 | 66.12 | 0.6786 |
| 4 | FD-BPNN | 35 | 12 | 0.006 | 81.82 | 79.18 | 0.8003 |
| 5 | SD-BPNN | 35 | 16 | 0.003 | 78.79 | 80.04 | 0.7705 |
| 6 | SD-SG-BPNN | 5 | 14 | 0.001 | 60.61 | 49.27 | 0.6451 |
| 10 | 14 | 0.001 | 63.64 | 52.01 | 0.7387 | ||
| 35 | 14 | 0.001 | 87.88 | 90.29 | 0.8755 | ||
| 7 | BPNN | 81 | 13 | 0.001 | 78.79 | 76.43 | 0.7758 |
| Reference | Object | Spectroscopy | Model | Evaluation Indicators |
|---|---|---|---|---|
| Ref. [4] | Apple | Vis/NIRS hyperspectral imaging | PLSR | R2 = 0.802, RMSE = ±0.674 °Brix (SSC) |
| Ref. [5] | Apple | Vis/NIRS hyperspectral imaging | PLS-DA | Accuracy of variety: 99.4% |
| Ref. [6] | Apple | NIRS | BP, GRNN1 | MAPE2 = 5.41% (acidity); MAPE = 13.95% (sweetness) |
| Ref. [7] | Apple | NIRS | PCA-DA | Accuracy of origin traceability: 93.6% (high-elevation), 77.9% (low-elevation) |
| Ref. [8] | Apple | Vis/SW-NIRS | SFS3, LDA | Accuracy range: 87.3–97.6% (firmness); 77.1–92.3% (SSC) |
| Ref. [9] | Apple | NIRS | PLS-DA | Classification accuracy = 96% |
| Ref. [10] | Apple | NIRS | DA | Classification accuracy = 91.3% (sweetness) |
| Ref. [11] | Apple | NIRS | SPA-LS-SVM | Classification accuracy = 90.11% (ripeness) |
| Ref. [12] | Shatian pomelo | Vis/NIRS | SG-MSC-GA-PCA-CNN-PLSR | R2 = 0.72, RMSE = 0.49 °Brix (SSC) R2 = 0.55, RMSE = 0.10% (acidity) |
| Ref. [13] | Wax apple | Vis/SW-NIRS | PLSR | Rp2 = 0.87, RMSEP = 0.66 °Brix(SSC) Rp2 = 0.80, RMSEP = 1.16 N/cm2 (firmness) |
| Ref. [14] | Apple | Vis/NIRS | MCARS4 and SPA-PLS | r = 0.946, RMSE = 0.527 °Brix for prediction set (SSC) |
| Ref. [15] | Golden apple | Vis/NIRS | LDA, QDA and SVM | Classification accuracy range: 75–81% (bitter pit) |
| Ref. [16] | Nectarine, peach, apricot and Japanese plums | Vis/NIRS | SD-PLSR | Classification accuracy: >75% (SSC, DMC and flesh firmness) |
| Ref. [45] | Maize | Vis/NIRS hyperspectral imaging | LDA and ANN | Classification accuracy: 95% (LDA), 85% (ANN) |
| Ref. [46] | Winter wheat | Vis/NIRS | SNV-SG-PLS and ANN | PLS: r = 0.92 and RMSE = 0.9131; ANN: r = 0.97 and RMSE = 0.7305 (LCC5) |
| Ref. [47] | Tomato | Vis/NIRS | PLS-DA | Accuracy of pesticide residue: 91.66% (prediction sets); SECV6 = 4.2767 |
| Ref. [48] | Potato | Vis/NIRS | PLS, ANN | Accuracy: PLS: 89% (SSC) and 93% (pH); ANN: 85% (SSC) and 90% (pH) |
| Ref. [49] | Potato | NIRS | PCA, PLS | R2 > 0.80 |
| Ours | Apple | Vis spectroscopy | SD-SG-PCA-PSO-BPNN | Classification accuracy: 100%; RMSEP = 0.112 °Brix; r = 0.998 (SSC) |
| Model | Pretreatment | LVs | Training Set | Testing Set | Leave-One-Out RMSECV (°Brix) | ||
|---|---|---|---|---|---|---|---|
| rcal | RMSEC (°Brix) | rpre | RMSEP (°Brix) | ||||
| PLSR | SD-SG | 5 | 0.388 | 1.597 | 0.527 | 1.540 | 1.3782 |
| 10 | 0.693 | 1.248 | 0.537 | 1.592 | 1.2117 | ||
| 35 | 0.824 | 0.981 | 0.758 | 1.417 | 1.3254 | ||
| BPNN | 35 | 0.991 | 0.224 | 0.814 | 1.107 | 0.8215 | |
| PSO-BPNN | 35 | 0.993 | 0.207 | 0.998 | 0.112 | 0.2693 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Ren, Z.; Wu, J.; Xiong, C.; Liu, L.; Sun, B.; Liang, G.; Zhou, M. Qualitative and Quantitative Assessments of Apple Quality Using Vis Spectroscopy Combined with Improved Particle-Swarm-Optimized Neural Networks. Foods 2023, 12, 1991. https://doi.org/10.3390/foods12101991
Peng W, Ren Z, Wu J, Xiong C, Liu L, Sun B, Liang G, Zhou M. Qualitative and Quantitative Assessments of Apple Quality Using Vis Spectroscopy Combined with Improved Particle-Swarm-Optimized Neural Networks. Foods. 2023; 12(10):1991. https://doi.org/10.3390/foods12101991
Chicago/Turabian StylePeng, Wenping, Zhong Ren, Junli Wu, Chengxin Xiong, Longjuan Liu, Bingheng Sun, Gaoqiang Liang, and Mingbin Zhou. 2023. "Qualitative and Quantitative Assessments of Apple Quality Using Vis Spectroscopy Combined with Improved Particle-Swarm-Optimized Neural Networks" Foods 12, no. 10: 1991. https://doi.org/10.3390/foods12101991
APA StylePeng, W., Ren, Z., Wu, J., Xiong, C., Liu, L., Sun, B., Liang, G., & Zhou, M. (2023). Qualitative and Quantitative Assessments of Apple Quality Using Vis Spectroscopy Combined with Improved Particle-Swarm-Optimized Neural Networks. Foods, 12(10), 1991. https://doi.org/10.3390/foods12101991