Thermal Degradation of Vegetable Oils
Abstract
:1. Introduction
2. Experimental Section
3. Results and Discussion
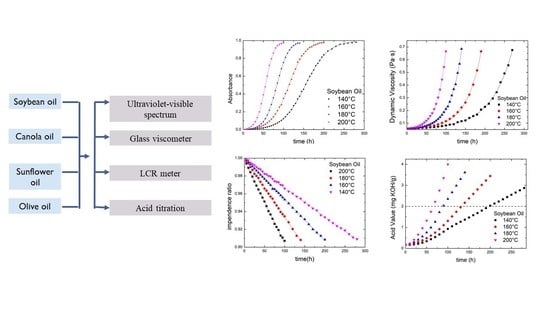
3.1. Ultraviolet-Visible Spectroscopy
3.2. Dynamic Viscosity
3.3. Electrical Impedance
3.4. Acid Value
3.5. Fourier Transform Infrared Spectroscopy (FTIR)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dupain, X.; Costa, D.J.; Schaverien, C.J.; Makkee, M.; Moulijn, J.A. Cracking of a rapeseed vegetable oil under realistic FCC conditions. Appl. Catal. B Environ. 2007, 72, 44–61. [Google Scholar] [CrossRef]
- Choe, E.; Min, D. Chemistry of deep-fat frying oils. J. Food Sci. 2007, 72, R77–R86. [Google Scholar] [CrossRef] [PubMed]
- Yen, P.-L.; Chen, B.-H.; Yang, F.L.; Lu, Y.-F. Effects of deep-frying oil on blood pressure and oxidative stress in spontaneously hypertensive and normotensive rats. Nutrition 2010, 26, 331–336. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yu, X.; Sun, D.; Li, J.; Wang, Y.; Cao, P.; Liu, Y. Effects of Polar Compounds Generated from the Deep-Frying Process of Palm Oil on Lipid Metabolism and Glucose Tolerance in Kunming Mice. J. Agric. Food Chem. 2016, 65, 208–215. [Google Scholar] [CrossRef] [PubMed]
- Cam, A.; Oyirifi, A.B.; Liu, Y.; Haschek, W.M.; Iwaniec, U.T.; Turner, R.T.; Engeseth, N.J.; Helferich, W.G. Thermally Abused Frying Oil Potentiates Metastasis to Lung in a Murine Model of Late-Stage Breast CancerThermally Abused Frying Oil Potentiates Me-tastasis to Lung. Cancer Prevent. Res. 2019, 12, 201–210. [Google Scholar] [CrossRef]
- Stott-Miller, M.; Neuhouser, M.L.; Stanford, J.L. Consumption of deep-fried foods and risk of prostate cancer. Prostate 2013, 73, 960–969. [Google Scholar] [CrossRef]
- Moros, J.; Roth, M.; Garrigues, S.; de la Guardia, M. Preliminary studies about thermal degradation of edible oils through attenuated total reflectance mid-infrared spectrometry. Food Chem. 2008, 114, 1529–1536. [Google Scholar] [CrossRef]
- Uncu, O.; Ozen, B.; Tokatli, F. Use of FTIR and UV–visible spectroscopy in determination of chemical characteristics of olive oils. Talanta 2019, 201, 65–73. [Google Scholar] [CrossRef]
- De la Mata, P.; Dominguez-Vidal, A.; Bosque-Sendra, J.M.; Ruiz-Medina, A.; Cuadros-Rodríguez, L.; Ayora-Cañada, M.J. Olive oil assessment in edible oil blends by means of ATR-FTIR and chemometrics. Food Control 2012, 23, 449–455. [Google Scholar] [CrossRef]
- Romano, R.; Giordano, A.; Le Grottaglie, L.; Manzo, N.; Paduano, A.; Sacchi, R.; Santini, A. Volatile compounds in intermittent frying by gas chromatography and nuclear magnetic resonance. Eur. J. Lipid Sci. Technol. 2013, 115, 764–773. [Google Scholar] [CrossRef]
- Caldwell, J.D.; Cooke, B.S.; Greer, M.K. High Performance Liquid Chromatography–Size Exclusion Chromatography for Rapid Analysis of Total Polar Compounds in Used Frying Oils. J. Am. Oil Chem. Soc. 2011, 88, 1669–1674. [Google Scholar] [CrossRef]
- Lazzerini, C.; Cifelli, M.; Domenici, V. Pigments in Extra-Virgin Olive Oil: Authenticity and Quality. In Products from Olive Tree; Books on Demand: McFarland, WI, USA, 2016. [Google Scholar] [CrossRef]
- Zhang, W.; Li, N.; Feng, Y.; Su, S.; Li, T.; Liang, B. A unique quantitative method of acid value of edible oils and studying the impact of heating on edible oils by UV–Vis spectrometry. Food Chem. 2015, 185, 326–332. [Google Scholar] [CrossRef]
- Khosroshahi, M.E. Effect of Temperature on Optical Properties of Vegetable Oils Using UV-Vis and Laser Fluorescence Spec-troscopy. Opt. Photon. J. 2018, 8, 247–263. [Google Scholar] [CrossRef]
- Jolayemi, O.S.; Tokatli, F.; Ozen, B. UV–Vis spectroscopy for the estimation of variety and chemical parameters of olive oils. J. Food Meas. Charact. 2021, 15, 4138–4149. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.; Liu, R.; Jin, Q.; Wang, X. Effect of frying conditions on fatty acid profile and total polar materials via viscosity. J. Food Eng. 2015, 166, 349–355. [Google Scholar] [CrossRef]
- Lioumbas, J.S.; Ampatzidis, C.; Karapantsios, T.D. Effect of potato deep-fat frying conditions on temperature dependence of olive oil and palm oil viscosity. J. Food Eng. 2012, 113, 217–225. [Google Scholar] [CrossRef]
- Firestone, D. Regulation of frying fat and oil. In Deep Frying; Elsevier: Amsterdam, The Netherlands, 2007; pp. 373–385. [Google Scholar]
- Advantec Company. Test Strips for Thermal Degradation of Frying Oils. Available online: https://www.advantec.co.jp/uploads/en/service_support/download/catalog/107-E-01-20060_AV-CHECK_A4.pdf (accessed on 6 July 2022).
- Šegatin, N.; Pajk Žontar, T.; Poklar Ulrih, N. Dielectric properties and dipole moment of edible oils subjected to ‘frying’ thermal treatment. Foods 2020, 9, 900. [Google Scholar] [CrossRef]
- Fendri, A.; Kallel, A.Y.; Nouri, H.; Ghariani, H.; Kanoun, O. Measurement System for Lossy Capacitive Sensors: Application to Edible Oils Quality Assessment. Sensors 2019, 19, 4299. [Google Scholar] [CrossRef]
- Khaled, A.Y.; Aziz, S.A.; Rokhani, F.Z. Capacitive sensor probe to assess frying oil degradation. Inf. Process. Agric. 2015, 2, 142–148. [Google Scholar] [CrossRef]
- ATAGO Company. Frying Oil Monitor DOM-24|Products—Frying Oil Monitor|ATAGO Co., Ltd. Available online: https://www.atago.net/en/products-dom-top.php (accessed on 6 July 2022).
- Wang, W.; Wang, Y.W.; Li, Z.X. Studies on Detection Device of Polar Components for Quality Evaluation of Frying Oil. Adv. Mater. Res. 2012, 562–564, 1815–1818. [Google Scholar] [CrossRef]
- Yang, C.-C.; Li, Y.-T.; Chiang, D.; Chiu, P.-K.; Lin, Y.-C.; Hsiao, W.-T. Comparison of Sensing Methods for Characterization of Heated Oils Degradation. In Proceedings of the 2021 IEEE Sensors Applications Symposium (SAS), Sundsvall, Sweden, 23–25 August 2021. [Google Scholar]
- Chiang, D.; Ding, C.-F.; Li, Y.-T.; Lin, Y.-C.; Chiu, P.-K.; Tsai, H.-Y. (Eds.) Assessment of frying oil degradation using laser direct writing interdigital sensors. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020. [Google Scholar]
- Ricca, M.; Foderà, V.; Vetri, V.; Buscarino, G.; Montalbano, M.; Leone, M. Oxidation Processes in Sicilian Olive Oils Investigated by a Combination of Optical and EPR Spectroscopy. J. Food Sci. 2012, 77, C1084–C1089. [Google Scholar] [CrossRef] [PubMed]
- Vlachos, N.; Skopelitis, Y.; Psaroudaki, M.; Konstantinidou, V.; Chatzilazarou, A.; Tegou, E. Applications of Fourier transform-infrared spectroscopy to edible oils. Anal. Chim. Acta 2006, 573–574, 459–465. [Google Scholar] [CrossRef] [PubMed]












| Temperature (°C) | αA (h−1) | A0 | A∞ | R2 |
|---|---|---|---|---|
| 200 | 0.091 | 0.0362 | 0.9632 | 0.998 |
| 180 | 0.068 | 0.0852 | 0.9951 | 0.997 |
| 160 | 0.047 | 0.0867 | 0.9774 | 0.996 |
| 140 | 0.035 | 0.0321 | 0.9675 | 0.997 |
| Oil Type | αA0 (h−1) | QA (kJ/mol) | R2 |
|---|---|---|---|
| Soybean | 58.34 | 25.44 | 0.995 |
| Canola | 69.18 | 26.17 | 0.994 |
| Olive | 14.58 | 20.99 | 0.998 |
| Sunflower | 31.98 | 23.40 | 0.997 |
| Annealing Time (°C) | φ0 (10−2 Pa·s) | φR (10−2 Pa·s) | φ0-φR(10−2 Pa·s) | αv (10−2 h−1) | R2 |
|---|---|---|---|---|---|
| 200 | 5.743 | 5.015 | 0.728 | 4.434 | 0.993 |
| 180 | 5.208 | 4.455 | 0.753 | 3.476 | 0.992 |
| 160 | 5.377 | 4.582 | 0.795 | 2.625 | 0.991 |
| 140 | 5.648 | 5.011 | 0.637 | 1.699 | 0.998 |
| Oil Type | αv0 (h−1) | Qv (kJ/mol) | R2 |
|---|---|---|---|
| Olive oil | 88.7 | 29.90 | 0.996 |
| Canola oil | 43.8 | 27.14 | 0.997 |
| Soybean oil | 30.4 | 25.77 | 0.996 |
| Sunflower oil | 17.8 | 23.58 | 0.998 |
| Oil Type | QE (kJ/mol) | R2 | |
|---|---|---|---|
| Soybean oil | 1.27 | 28.44 (±0.53) | 0.997 |
| Canola oil | 0.90 | 28.44 (±0.49) | 0.998 |
| Olive oil | 1.20 | 28.66 (±0.58) | 0.995 |
| Sunflower oil | 1.32 | 28.32 (±0.45) | 0.997 |
| Oil Type | tA0 (h) | QAC (kJ/mol) | R2 |
|---|---|---|---|
| Olive | 0.0192 | 30.9 | 0.997 |
| Canola | 0.0239 | 30.4 | 0.996 |
| Sunflower | 0.0369 | 29.0 | 0.995 |
| Soybean | 0.0392 | 29.1 | 0.996 |
| Wavenumber (cm−1) | Description |
|---|---|
| 3008 cm−1 | C-H stretching vibration of the cis-double bond (=CH) |
| 2924 cm−1, 2854 cm−1 | Symmetric and asymmetric stretching vibration of the aliphatic CH2 group |
| 1745 cm−1 | Ester carbonyl functional group of the Triglycerides |
| 1464 cm−1 | Bending vibrations of the CH2 and CH3 aliphatic groups |
| 1417 cm−1 | Rocking vibrations of CH bonds of cis-disubstituted olefins |
| 1399 cm−1 | Bending in-ddplane vibrations of CH cis-olefinic groups |
| 1323 cm−1 | The extra peak appears in mixed oil. |
| 1244 cm−1, 1162 cm−1, 1100 cm−1 | Stretching vibration of the C-O ester Groups |
| 1120 cm−1 | Aliphatic ethers |
| 840.5 cm−1 | trisubstituted alkenes |
| 720 cm−1 | Overlapping of the CH2 rocking vibration and the out-of-plane vibration of cis-disubstituted olefins |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, Y.-H.; Chiang, D.; Li, Y.-T.; Perng, T.-P.; Lee, S. Thermal Degradation of Vegetable Oils. Foods 2023, 12, 1839. https://doi.org/10.3390/foods12091839
Tsai Y-H, Chiang D, Li Y-T, Perng T-P, Lee S. Thermal Degradation of Vegetable Oils. Foods. 2023; 12(9):1839. https://doi.org/10.3390/foods12091839
Chicago/Turabian StyleTsai, Yi-Hsiou, Donyau Chiang, Yu-Ting Li, Tsong-Pyng Perng, and Sanboh Lee. 2023. "Thermal Degradation of Vegetable Oils" Foods 12, no. 9: 1839. https://doi.org/10.3390/foods12091839
APA StyleTsai, Y. -H., Chiang, D., Li, Y. -T., Perng, T. -P., & Lee, S. (2023). Thermal Degradation of Vegetable Oils. Foods, 12(9), 1839. https://doi.org/10.3390/foods12091839