Unsupervised Learning-Based Non-Invasive Fetal ECG Muti-Level Signal Quality Assessment
Abstract
:1. Introduction
2. Related Work
3. Preliminaries
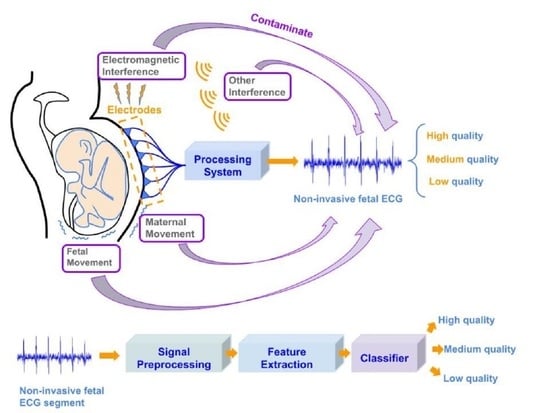
3.1. Non-Invasive Fetal ECG
3.2. Short-Time Fourier Transform
3.3. Autoencoder
3.4. Self-Organizing Map
- Initialize all the weight vectors randomly.
- Select an input sample from the training set .
- By computing the Euclidean distance for each neuron k, compare with the weights . The neuron with the shortest distance is declared as the winning neuron.
- After updating the weights of neurons, the winning neuron should resemble the input vector .
- The weight vectors of neighboring neurons are changed to more closely resemble the input vector. A weight vector changes more as the neuron gets closer to the winning neuron.
4. Proposed Method
4.1. Data Acquisition
4.2. Signal Pre-Processing
4.3. Feature Extraction
4.3.1. AE-Based Feature
4.3.2. Entropy-Based Features
- Approximate entropy (AppEn): AppEn is a common-use feature for quantifying irregularity in time series data with no knowledge about the system. Larger values of AppEn correspond to more complexity and irregularity in the data [14].
- Sample entropy (SampEn): To overcome the shortcomings of AppEn, including heavy dependency on the length of the recording and lack of relative consistency, SampEn was introduced. Compared with AppEn, SampEn avoids self-matches, so it can be independent of the length of recordings and extract relative consistency [15].
- Spectral entropy (SpecEn): Spectral entropy, based on Shannon entropy, can quantify the regularity or uncertainty of the power spectrum during a specific period. In actuality, the regularity of the power spectrum distribution is mirrored in spectral entropy. The higher SpecEn indicates a more uniform power spectrum distribution [16].
- Permutation entropy (PEn): A continuous time series can be transformed into a symbolic sequence using the permutation approach, and PEn is the output of the statistics of the symbolic sequences. PEn of time series data, which can be calculated simply and quickly, contains temporal information [17].
4.3.3. Statistical Features
- Detrended fluctuation analysis (DFA): The main purpose of DFA is to extract long-range correlation in non-stationary time series. Many researchers have used DFA for analyzing cardiac interbeat intervals [18].
- Fractal dimension (FD): FD is a quantitative metric used in biomedical signal processing to gauge the complexity of discrete temporal physiological data. FD can aid in the understanding of physiological processes [19].
- Higuchi fractal dimension (HFD): Higuchi’s approach to FD calculation is proved to reach accurate and reliable estimation results, which is called HFD. This technique can be used to compute moving window estimates of FD for non-stationary signals by segmenting signals into brief quasi-stationary frames. It is also suited for estimating FD of segments with a short time duration of time series [19].
4.3.4. ECG SQIs
4.4. Multi-Level Signal Quality Classification
- Size of output layer: 8 × 8.
- Initial value of learning rate: 0.5.
- The number of iterations: 100,000.
- Neighborhood function: bubble.
4.5. Performance Evaluation
4.5.1. For Classification Performance
- Precision: the proportion of the FECG segments correctly predicted as one class in all the FECG segments predicted as the class.
- Recall: the proportion of the FECG segments correctly predicted as one class in all the FECG segments labeled as the class.
- F1-score: the harmonic mean of precision and recall.
4.5.2. For Improvement of FHR Estimation
- Root mean square error (RMSE) between the estimated fetal RR interval (FRRI) value and the reference value , which is given as follows:where is the number of the FECG signal segments for the estimated FRRIs.
- Averaged absolute error (AAE) between the estimated value and the reference valuewhere denotes the sampling frequency of the FECG recordings.
- The removal rate, which is the proportion of the removed FHRs through the method over all the estimated FHRs.
5. Results and Discussion
5.1. Feature Evaluation
5.2. Classification Evaluation
5.3. Improvement of FHR Estimation
5.4. Limitation and Future Works
5.4.1. About the Number of Quality Levels
5.4.2. About the Unbalanced Dataset
5.4.3. About the Coverage
5.4.4. About Practical Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zarzoso, V.; Nandi, A.K. Noninvasive fetal electrocardiogram extraction: Blind separation versus adaptive noise cancellation. IEEE Trans. Biomed. Eng. 2001, 48, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Kumari, N.; Acharjya, D.P. Data classification using rough set and bioinspired computing in healthcare applications—An extensive review. Multimed Tools Appl. 2022, 1–27. [Google Scholar] [CrossRef]
- Reiss, A.; Indlekofer, I.; Schmidt, P.; Van Laerhoven, K. Deep PPG: Large-scale heart rate estimation with convolutional neural networks. Sensors 2019, 19, 3079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oh, S.L.; Hagiwara, Y.; Raghavendra, U.; Yuvaraj, R.; Arunkumar, N.; Murugappan, M.; Acharya, U.R. A deep learning approach for Parkinson’s disease diagnosis from EEG signals. Neural Comput. Appl. 2020, 32, 10927–10933. [Google Scholar] [CrossRef]
- Eom, H.; Lee, D.; Han, S.; Hariyani, Y.S.; Lim, Y.; Sohn, I.; Park, K.; Park, C. End-to-End Deep Learning Architecture for Continuous Blood Pressure Estimation Using Attention Mechanism. Sensors 2020, 20, 2338. [Google Scholar] [CrossRef] [Green Version]
- Bhavanasi, G.; Werthen-Brabants, L.; Dhaene, T.; Couckuyt, I. Patient activity recognition using radar sensors and machine learning. Neural Comput. Appl. 2022, 34, 16033–16048. [Google Scholar] [CrossRef]
- Clifford, G.D.; Behar, J.; Li, Q.; Rezek, I. Signal Quality Indices and data fusion for determining clinical acceptability of electrocardiograms. Physiol. Meas. 2012, 33, 1419–1433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Q.; Rajagopalan, C.; Clifford, G.D. A machine learning approach to multi-level ECG signal quality classification. Comput. Methods Programs Biomed. 2014, 117, 435–447. [Google Scholar] [CrossRef]
- Huerta, A.; Martinez-Rodrigo, A.; Gonzalez, V.B.; Quesada, A.; Rieta, J.J.; Alcaraz, R. Quality Assessment of very long-term ECG recordings using a convolutional neural network. In Proceedings of the 2019 E-Health and Bioengineering Conference (EHB), Iasi, Romania, 21–23 November 2019; pp. 1–4. [Google Scholar]
- Seeuws, N.; De Vos, M.; Bertrand, A. Electrocardiogram quality assessment using unsupervised deep learning. IEEE Trans. Biomed. Eng. 2021, 69, 882–893. [Google Scholar] [CrossRef]
- Rahmati, A.K.; Setarehdan, S.K.; Araabi, B.N. A PCA/ICA based Fetal ECG Extraction from Mother Abdominal Recordings by Means of a Novel Data-driven Approach to Fetal ECG Quality Assessment. J. Biomed. Phys. Eng. 2017, 7, 37–50. [Google Scholar]
- Andreotti, F.; Grasser, F.; Malberg, H.; Zaunseder, S. Non-invasive fetal ECG signal quality assessment for Multichannel Heart Rate Estimation. IEEE Trans. Biomed. Eng. 2017, 64, 2793–2802. [Google Scholar] [CrossRef] [PubMed]
- Fotiadou, E.; van Sloun, R.J.; van Laar, J.O.; Vullings, R. A dilated inception CNN-LSTM network for fetal heart rate estimation. Physiol. Meas. 2021, 42, 045007. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. In Proceedings of the 1991 IEEE Seventeenth Annual Northeast Bioengineering Conference, Hartford, CT, USA, 4–5 April 1991; Volume 88, pp. 2297–2301. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lind, N. Entropy optimization principles with applications. Struct. Saf. 1993, 12, 243–244. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Jospin, M.; Caminal, P.; Jensen, E.W.; Litvan, H.; Vallverdu, M.; Struys, M.M.R.F.; Vereecke, H.E.M.; Kaplan, D.T. Detrended fluctuation analysis of EEG as a measure of depth of anesthesia. IEEE Trans. Biomed. Eng. 2007, 54, 840–846. [Google Scholar] [CrossRef]
- Esteller, R.; Vachtsevanos, G.; Echauz, J.; Litt, B. A comparison of waveform fractal dimension algorithms. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 177–183. [Google Scholar] [CrossRef] [Green Version]
- Cai, D.; Zhang, C.; He, X. Unsupervised Feature Selection for Multi-Cluster Data. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 333–342. [Google Scholar]
- Shi, X.; Yamamoto, K.; Ohtsuki, T.; Matsui, Y.; Owada, K. Non-invasive Fetal ECG Signal Quality Assessment based on Unsupervised Learning Approach. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11–15 July 2022; pp. 1296–1299. [Google Scholar]
- Lee, M.Y.; Won, H.S. Technique of fetal echocardiography. Obstet. Gynecol. Sci. 2013, 56, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Grivell, R.M.; Alfirevic, Z.; Gyte, G.M.L.; Devane, D. Antenatal cardiotocography for fetal assessment. Cochrane Database Syst. Rev. 2015, 2015, CD007863. [Google Scholar] [CrossRef]
- Hasan, M.A.; Reaz, M.B.I.; Ibrahimy, M.I.; Hussain, M.S.; Uddin, J. Detection and processing techniques of FECG signal for fetal monitoring. Biol. Proced. Online 2009, 11, 263–295. [Google Scholar] [CrossRef] [Green Version]
- Norén, H.; Blad, S.; Carlsson, A.; Flisberg, A.; Gustavsson, A.; Lilja, H.; Wennergren, M.; Hagberg, H. Stan in clinical practice—The outcome of 2 years of regular use in the city of Gothenburg. Am. J. Obstet. Gynecol. 2006, 195, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, G.; Wei, Y. Non-invasive fetal electrocardiogram monitoring techniques: Potential and future research opportunities in smart textiles. Signals 2021, 2, 392–412. [Google Scholar] [CrossRef]
- Behar, J.A.; Bonnemains, L.; Shulgin, V.; Oster, J.; Ostras, O.; Lakhno, I. Noninvasive fetal electrocardiography for the detection of fetal arrhythmias. Prenat. Diagn. 2019, 39, 178–187. [Google Scholar] [CrossRef] [PubMed]
- Rui, T.; Zhang, S.; Ren, T.; Tang, J.; Zou, J. Data Reconstruction based on supervised deep auto-encoder. In Pacific Rim Conference on Multimedia; Springer: Cham, Switzerland, 2018; pp. 869–879. [Google Scholar]
- Roy, M.S.; Gupta, R.; Sharma, K.D. Photoplethysmogram signal quality evaluation by unsupervised learning approach. In Proceedings of the 2020 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 October 2020; pp. 6–10. [Google Scholar]
- Ghosal, P.; Sarkar, D.; Kundu, S.; Roy, S.; Sinha, A.; Ganguli, S. ECG beat Quality Assessment Using Self Organizing Map. In Proceedings of the 2017 4th International Conference on Opto-Electronics and Applied Optics (Optronix), Kolkata, India, 2–3 November 2017; pp. 1–5. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Oshio, S.; Kimura, Y.; Nishigori, H.; Sato, N.; Minato, T.; Khandoker, A.H.; Owada, K.; Sudo, K.; Odagiri, N.; Yaegashi, N. A comparison study on safety and efficacy of maternal abdominal-lead fetal ecg under regulatory science. Adv. Clin. Transl. Res 2018, 2, 1–12. [Google Scholar]
- Kimura, Y.; Ito, T.; Matuyama, F.; Chida, S.; Katayama, N.; Nakao, M.; Okamura, K. Measurement method for the fetal electrocardiogram. Minim Invasive Ther. Allied. Technol. 2006, 15, 214–217. [Google Scholar] [CrossRef]
- Niida, N.; Wang, L.; Ohtsuki, T.; Owada, K.; Honma, N.; Hayashi, H. Fetal Heart Rate Detection Using First Derivative of ECG Waveform and Multiple Weighting Functions. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Virtual, 1–5 November 2021; pp. 434–438. [Google Scholar]
- Valderrama, C.E.; Stroux, L.; Katebi, N.; Paljug, E.; Hall-Clifford, R.; Rohloff, P.; Marzbanrad, F.; Clifford, G.D. An Open Source Autocorrelation-based Method for Fetal Heart Rate Estimation from One-Dimensional Doppler Ultrasound. Physiol. Meas. 2019, 40, 025005. [Google Scholar] [CrossRef]
- Yamamoto, K.; Toyoda, K.; Ohtsuki, T. Spectrogram-based non-contact RRI estimation by accurate peak detection algorithm. IEEE Access 2018, 6, 60369–60379. [Google Scholar] [CrossRef]
- Borowska, M. Entropy-based algorithms in the analysis of biomedical signals. Stud. Logic Gramm. Rhetor. 2015, 43, 21–32. [Google Scholar] [CrossRef] [Green Version]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Kohonen, T.; Nieminen, I.T.; Honkela, T. On the quantization error in SOM vs. VQ: A critical and systematic study. In Advances in Self-Organizing Maps; Springer: Berlin/Heidelberg, Germany, 2009; pp. 133–144. [Google Scholar]
- Varanini, M.; Tartarisco, G.; Billeci, L.; Macerata, A.; Pioggia, G.; Balocchi, R. A multi-step approach for non-invasive fetal ECG analysis. Comput. Cardiol. 2013, 2013, 281–284. [Google Scholar]








| Precision | Recall | F1-Score | ||
|---|---|---|---|---|
| K-means | Medium | 0.61 | 0.78 | 0.68 |
| High | 0.80 | 0.75 | 0.78 | |
| Low | 0.88 | 0.69 | 0.77 | |
| Average | 0.76 | 0.74 | 0.74 | |
| K-means++ | Medium | 0.61 | 0.77 | 0.68 |
| High | 0.80 | 0.75 | 0.78 | |
| Low | 0.87 | 0.69 | 0.77 | |
| Average | 0.76 | 0.74 | 0.74 | |
| Hierarchy Clustering | Medium | 0.55 | 0.91 | 0.69 |
| High | 0.88 | 0.68 | 0.77 | |
| Low | 0.97 | 0.56 | 0.71 | |
| Average | 0.80 | 0.72 | 0.72 | |
| Spectral Clustering | Medium | 0.55 | 0.80 | 0.65 |
| High | 0.79 | 0.74 | 0.76 | |
| Low | 0.87 | 0.53 | 0.66 | |
| Average | 0.74 | 0.69 | 0.69 | |
| SOM | Medium | 0.85 | 0.85 | 0.85 |
| High | 0.92 | 0.96 | 0.94 | |
| Low | 0.92 | 0.88 | 0.90 | |
| Average | 0.90 | 0.90 | 0.90 |
| No Removal | With Removal | ||||
|---|---|---|---|---|---|
| Subject | RMSE [ms] | AAE [bpm] | RMSE [ms] | AAE [bpm] | Removal Rate |
| 1 | 0.0047 | 0.4835 | 0.0033 | 0.3045 | 21.61% |
| 2 | 0.0075 | 1.0433 | 0.0038 | 0.4722 | 27.47% |
| 3 | 0.0018 | 0.3687 | 0.0016 | 0.3472 | 8.42% |
| 4 | 0.0021 | 0.3447 | 0.0020 | 0.3334 | 9.52% |
| 5 | 0.0033 | 0.3478 | 0.0029 | 0.3212 | 7.69% |
| 6 | 0.0010 | 0.2133 | 0.0010 | 0.2043 | 10.26% |
| 7 | 0.0019 | 0.2915 | 0.0011 | 0.2264 | 13.19% |
| 8 | 0.0191 | 1.2037 | 0.0193 | 1.0410 | 9.52% |
| 9 | 0.0078 | 1.0200 | 0.0075 | 0.9871 | 12.09% |
| 10 | 0.0036 | 0.3664 | 0.0011 | 0.2130 | 12.09% |
| Average | 0.0053 | 0.5683 | 0.0044 | 0.4450 | 13.18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Yamamoto, K.; Ohtsuki, T.; Matsui, Y.; Owada, K. Unsupervised Learning-Based Non-Invasive Fetal ECG Muti-Level Signal Quality Assessment. Bioengineering 2023, 10, 66. https://doi.org/10.3390/bioengineering10010066
Shi X, Yamamoto K, Ohtsuki T, Matsui Y, Owada K. Unsupervised Learning-Based Non-Invasive Fetal ECG Muti-Level Signal Quality Assessment. Bioengineering. 2023; 10(1):66. https://doi.org/10.3390/bioengineering10010066
Chicago/Turabian StyleShi, Xintong, Kohei Yamamoto, Tomoaki Ohtsuki, Yutaka Matsui, and Kazunari Owada. 2023. "Unsupervised Learning-Based Non-Invasive Fetal ECG Muti-Level Signal Quality Assessment" Bioengineering 10, no. 1: 66. https://doi.org/10.3390/bioengineering10010066
APA StyleShi, X., Yamamoto, K., Ohtsuki, T., Matsui, Y., & Owada, K. (2023). Unsupervised Learning-Based Non-Invasive Fetal ECG Muti-Level Signal Quality Assessment. Bioengineering, 10(1), 66. https://doi.org/10.3390/bioengineering10010066