An Attempt to Predict the Preferential Cellular Orientation in Any Complex Mechanical Environment
Abstract
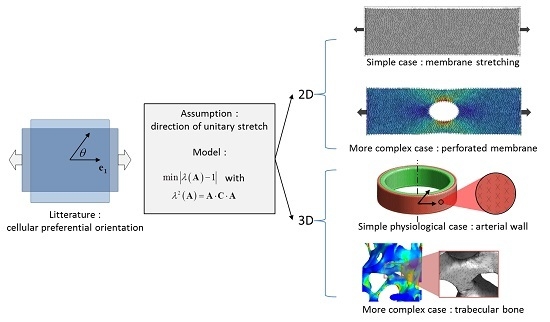
:1. Introduction
2. Materials and Methods
2.1. Calculation of Unitary Stretch and Numerical Implementation
2.2. Numerical Implementation
2.3. Planar Case: Stretching of a Membrane
2.4. Physiological Case: Inflation of an Arterial Segment
2.5. Illustration for a Complex 2D Mechanical Environment: Stretching of a Perforated Membrane
2.6. Illustration for a Complex 3D Mechanical Environment: Compression of a Trabecular Bone Sample
3. Results
3.1. Simple Example: Sensitivity to Poisson’s Ratio in Uniaxial Tension
3.2. Planar Case: Stretching of a Membrane
3.3. Physiological Case: Inflation of an Arterial Segment
3.4. Illustration for a Complex 2D Mechanical Environment: Stretching of a Perforated Membrane
3.5. Illustration for a Complex 3D Mechanical Environment: Compression of a Trabecular Bone Sample
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Liu, Y.-S.; Lee, O.K. In Search of the Pivot Point of Mechanotransduction: Mechanosensing of Stem Cells. Cell Transplant. 2014, 23, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Skardal, A.; Mack, D.; Atala, A.; Soker, S. Substrate elasticity controls cell proliferation, surface marker expression and motile phenotype in amniotic fluid-derived stem cells. J. Mech. Behav. Biomed. Mater. 2013, 17, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J.; Dufresne, E.; Schwartz, M. Mechanotransduction and extracellular matrix homeostasis. Nat. Rev. Mol. Cell Biol. 2014, 15, 802–812. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D.E. Cellular mechanotransduction: Putting all the pieces together again. FASEB J. 2006, 20, 811–827. [Google Scholar] [CrossRef] [PubMed]
- Ricca, B.L.; Venugopalan, G.; Fletcher, D.A. To pull or be pulled: Parsing the multiple modes of mechanotransduction. Curr. Opin. Cell Biol. 2013, 25, 558–564. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.H.-C.; Jia, F.; Gilbert, T.W.; Woo, S.L.-Y. Cell orientation determines the alignment of cell-produced collagenous matrix. J. Biomech. 2003, 36, 97–102. [Google Scholar] [CrossRef]
- Jungbauer, S.; Gao, H.; Spatz, J.P.; Kemkemer, R. Two Characteristic Regimes in Frequency-Dependent Dynamic Reorientation of Fibroblasts on Cyclically Stretched Substrates. Biophys. J. 2008, 95, 3470–3478. [Google Scholar] [CrossRef] [PubMed]
- Livne, A.; Bouchbinder, E.; Geiger, B. Cell reorientation under cyclic stretching. Nat. Commun. 2014, 5, 3938. [Google Scholar] [CrossRef] [PubMed]
- Nagayama, K.; Kimura, Y.; Makino, N.; Matsumoto, T. Strain waveform dependence of stress fiber reorientation in cyclically stretched osteoblastic cells: Effects of viscoelastic compression of stress fibers. Am. J. Physiol. Cell Physiol. 2012, 302, C1469–C1478. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ip, W.; Boissy, R.; Grood, E.S. Cell orientation response to cyclically deformed substrates: Experimental validation of a cell model. J. Biomech. 1995, 28, 1543–1552. [Google Scholar] [CrossRef]
- Wang, J.H.-C.; Goldschmidt-Clermont, P.; Wille, J.; Yin, F.C.-P. Specificity of endothelial cell reorientation in response to cyclic mechanical stretching. J. Biomech. 2001, 34, 1563–1572. [Google Scholar] [CrossRef]
- Zhang, L.; Kahn, C.J.F.; Chen, H.-Q.; Tran, N.; Wang, X. Effect of uniaxial stretching on rat bone mesenchymal stem cell: Orientation and expressions of collagen types I and III and tenascin-C. Cell Biol. Int. 2008, 32, 344–352. [Google Scholar] [CrossRef] [PubMed]
- Kanda, K.; Matsuda, T.; Oka, T. Two-dimensional orientational response of smooth muscle cells to cyclic stretching. ASAIO J. Am. Soc. Artif. Intern. Organs 1992, 38, M382–M385. [Google Scholar] [CrossRef]
- Wang, J.H.-C. Substrate Deformation Determines Actin Cytoskeleton Reorganization: A Mathematical Modeling and Experimental Study. J. Theor. Biol. 2000, 202, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Buck, R.C. Reorientation response of cells to repeated stretch and recoil of the substratum. Exp. Cell Res. 1980, 127, 470–474. [Google Scholar] [CrossRef]
- Faust, U.; Hampe, N.; Rubner, W.; Kirchgeßner, N.; Safran, S.; Hoffmann, B.; Merkel, R. Cyclic Stress at mHz Frequencies Aligns Fibroblasts in Direction of Zero Strain. PLoS ONE 2011, 6, e28963. [Google Scholar] [CrossRef] [PubMed]
- Standley, P.R.; Camaratta, A.; Nolan, B.P.; Purgason, C.T.; Stanley, M.A. Cyclic stretch induces vascular smooth muscle cell alignment via NO signaling. Am. J. Physiol. Heart Circ. Physiol. 2002, 283, H1907–H1914. [Google Scholar] [CrossRef] [PubMed]
- Rudnicki, J.W. Fundamentals of Continuum Mechanics, 1st ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley-Blackwell: Chichester, UK; New York, NY, USA, 2000. [Google Scholar]
- Lefever, J.A.; Jaime García, J.; Smith, J.H. A patient-specific, finite element model for noncommunicating hydrocephalus capable of large deformation. J. Biomech. 2013, 46, 1447–1453. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C. Computational stress-deformation analysis of arterial walls including high-pressure response. Int. J. Cardiol. 2007, 116, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. Lond. Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Jiu-sheng, R. Effects of dispersion of fiber orientation on the mechanical property of the arterial wall. J. Theor. Biol. 2012, 301, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Navidbakhsh, M.; Shojaei, A.; Faghihi, S. Measurement of the uniaxial mechanical properties of healthy and atherosclerotic human coronary arteries. Mater. Sci. Eng. C 2013, 33, 2550–2554. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar]
- Grant, C.A.; Twigg, P.C.; Tobin, D.J. Static and dynamic nanomechanical properties of human skin tissue using atomic force microscopy: Effect of scarring in the upper dermis. Acta Biomater. 2012, 8, 4123–4129. [Google Scholar] [CrossRef] [PubMed]
- Buganza Tepole, A. Computational systems mechanobiology of wound healing. Comput. Methods Appl. Mech. Eng. 2017, 314, 46–70. [Google Scholar] [CrossRef]
- Assidi, M.; Ganghoffer, J.-F. Composites with auxetic inclusions showing both an auxetic behavior and enhancement of their mechanical properties. Compos. Struct. 2012, 94, 2373–2382. [Google Scholar] [CrossRef]
- Dos Reis, F.; Ganghoffer, J.F. Equivalent mechanical properties of auxetic lattices from discrete homogenization. Comput. Mater. Sci. 2012, 51, 314–321. [Google Scholar] [CrossRef]
- Tondon, A.; Kaunas, R. The Direction of Stretch-Induced Cell and Stress Fiber Orientation Depends on Collagen Matrix Stress. PLoS ONE 2014, 9, e89592. [Google Scholar] [CrossRef] [PubMed]
- Laurent, C.P.; Vaquette, C.; Martin, C.; Guedon, E.; Wu, X.; Delconte, A.; Dumas, D.; Hupont, S.; Isla, N.D.; Rahouadj, R.; et al. Towards a Tissue-Engineered Ligament: Design and Preliminary Evaluation of a Dedicated Multi-Chamber Tension-Torsion Bioreactor. Processes 2014, 2, 167–179. [Google Scholar] [CrossRef]
- Milan, J.-L.; Planell, J.A.; Lacroix, D. Simulation of bone tissue formation within a porous scaffold under dynamic compression. Biomech. Model. Mechanobiol. 2010, 9, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Sandino, C.; Lacroix, D. A dynamical study of the mechanical stimuli and tissue differentiation within a CaP scaffold based on micro-CT finite element models. Biomech. Model. Mechanobiol. 2011, 10, 565–576. [Google Scholar] [CrossRef] [PubMed]
- Laurent, C.P.; Latil, P.; Durville, D.; Rahouadj, R.; Geindreau, C.; Orgéas, L.; Ganghoffer, J.-F. Mechanical behaviour of a fibrous scaffold for ligament tissue engineering: Finite elements analysis vs. X-ray tomography imaging. J. Mech. Behav. Biomed. Mater. 2014, 40, 222–233. [Google Scholar] [CrossRef] [PubMed]
- Laurent, C.P.; Durville, D.; Mainard, D.; Ganghoffer, J.-F.; Rahouadj, R. A multilayer braided scaffold for Anterior Cruciate Ligament: Mechanical modeling at the fiber scale. J. Mech. Behav. Biomed. Mater. 2012, 12, 184–196. [Google Scholar] [CrossRef] [PubMed]
- Nakaoka, S.; Aihara, K. Stochastic simulation of structured skin cell population dynamics. J. Math. Biol. 2013, 66, 807–835. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.J.; Landman, K.A.; Bhaganagarapu, K. Coalescence of interacting cell populations. J. Theor. Biol. 2007, 247, 525–543. [Google Scholar] [CrossRef] [PubMed]
- Arino, O.; Kimmel, M. Comparison of Approaches to Modeling of Cell Population Dynamics. SIAM J. Appl. Math. 1993, 53, 1480–1504. [Google Scholar] [CrossRef]
- Sanz-Herrera, J.A.; Moreo, P.; García-Aznar, J.M.; Doblaré, M. On the effect of substrate curvature on cell mechanics. Biomaterials 2009, 30, 6674–6686. [Google Scholar] [CrossRef] [PubMed]
- Martínez, E.; Engel, E.; Planell, J.A.; Samitier, J. Effects of artificial micro- and nano-structured surfaces on cell behaviour. Ann. Anat. Anat. Anz. 2009, 191, 126–135. [Google Scholar] [CrossRef] [PubMed]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laurent, C.P.; Ganghoffer, J.-F.; Rahouadj, R. An Attempt to Predict the Preferential Cellular Orientation in Any Complex Mechanical Environment. Bioengineering 2017, 4, 16. https://doi.org/10.3390/bioengineering4010016
Laurent CP, Ganghoffer J-F, Rahouadj R. An Attempt to Predict the Preferential Cellular Orientation in Any Complex Mechanical Environment. Bioengineering. 2017; 4(1):16. https://doi.org/10.3390/bioengineering4010016
Chicago/Turabian StyleLaurent, Cédric P, Jean-François Ganghoffer, and Rachid Rahouadj. 2017. "An Attempt to Predict the Preferential Cellular Orientation in Any Complex Mechanical Environment" Bioengineering 4, no. 1: 16. https://doi.org/10.3390/bioengineering4010016
APA StyleLaurent, C. P., Ganghoffer, J. -F., & Rahouadj, R. (2017). An Attempt to Predict the Preferential Cellular Orientation in Any Complex Mechanical Environment. Bioengineering, 4(1), 16. https://doi.org/10.3390/bioengineering4010016