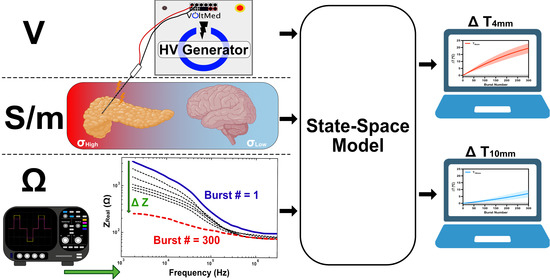
Real-Time Temperature Rise Estimation during Irreversible Electroporation Treatment through State-Space Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. AGAR Model
2.2. Treatment Parameters
2.3. Real-Time Impedance Acquisition
2.4. Temperature Acquisition
2.5. Data Processing
2.6. Development of the Mathematical Model
2.7. Validation of the Mathematical Model against FEM
3. Results
3.1. Experimental Data Results
3.2. Model Validation with Training and Validation Data Sets
3.3. Model Implementation with Test Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FAST | Fourier Analysis SpecTroscopy |
| FEM | Finite Element Modeling |
| H-FIRE | High-Frequency Irreversible Electroporation |
| IRE | Irreversible Electroporation |
| N4SID | Numerical Algorithms for Subspace State-Space Identification |
| PEF | Pulsed Electric Field |
| SSM | State-Space Model |
Appendix A
N4sid Oblique Projection by LQ Decomposition
References
- Geboers, B.; Scheffer, H.J.; Graybill, P.M.; Ruarus, A.H.; Nieuwenhuizen, S.; Puijk, R.S.; van den Tol, P.M.; Davalos, R.V.; Rubinsky, B.; de Gruijl, T.D.; et al. High-voltage electrical pulses in oncology: Irreversible electroporation, electrochemotherapy, gene electrotransfer, electrofusion, and electroimmunotherapy. Radiology 2020, 295, 254–272. [Google Scholar] [CrossRef]
- Maor, E.; Sugrue, A.; Witt, C.; Vaidya, V.R.; DeSimone, C.V.; Asirvatham, S.J.; Kapa, S. Pulsed electric fields for cardiac ablation and beyond: A state-of-the-art review. Heart Rhythm 2019, 16, 1112–1120. [Google Scholar] [CrossRef] [PubMed]
- Wittkampf, F.H.; van Es, R.; Neven, K. Electroporation and its relevance for cardiac catheter ablation. JACC Clin. Electrophysiol. 2018, 4, 977–986. [Google Scholar] [CrossRef] [PubMed]
- Weaver, J.C.; Smith, K.C.; Esser, A.T.; Son, R.S.; Gowrishankar, T. A brief overview of electroporation pulse strength–duration space: A region where additional intracellular effects are expected. Bioelectrochemistry 2012, 87, 236–243. [Google Scholar] [CrossRef]
- Yarmush, M.L.; Golberg, A.; Serša, G.; Kotnik, T.; Miklavčič, D. Electroporation-based technologies for medicine: Principles, applications, and challenges. Annu. Rev. Biomed. Eng. 2014, 16, 295–320. [Google Scholar] [CrossRef]
- Weaver, J.C. Electroporation: A general phenomenon for manipulating cells and tissues. J. Cell. Biochem. 1993, 51, 426–435. [Google Scholar] [CrossRef]
- Mercadal, B.; Beitel-White, N.; Aycock, K.N.; Castellví, Q.; Davalos, R.V.; Ivorra, A. Dynamics of cell death after conventional IRE and H-FIRE treatments. Ann. Biomed. Eng. 2020, 48, 1451–1462. [Google Scholar] [CrossRef]
- Napotnik, T.B.; Polajžer, T.; Miklavčič, D. Cell death due to electroporation–a review. Bioelectrochemistry 2021, 141, 107871. [Google Scholar] [CrossRef] [PubMed]
- Davalos, R.V.; Mir, L.; Rubinsky, B. Tissue ablation with irreversible electroporation. Ann. Biomed. Eng. 2005, 33, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Faroja, M.; Ahmed, M.; Appelbaum, L.; Ben-David, E.; Moussa, M.; Sosna, J.; Nissenbaum, I.; Goldberg, S.N. Irreversible electroporation ablation: Is all the damage nonthermal? Radiology 2013, 266, 462–470. [Google Scholar] [CrossRef]
- Van Den Bos, W.; Scheffer, H.J.; Vogel, J.A.; Wagstaff, P.G.; De Bruin, D.M.; De Jong, M.C.; Van Gemert, M.J.; De La Rosette, J.J.; Meijerink, M.R.; Klaessens, J.H.; et al. Thermal energy during irreversible electroporation and the influence of different ablation parameters. J. Vasc. Interv. Radiol. 2016, 27, 433–443. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Moser, M.; Zhang, E.; Zhang, W.; Zhang, B. Optimization of electrode configuration and pulse strength in irreversible electroporation for large ablation volumes without thermal damage. J. Eng. Sci. Med. Diagn. Ther. 2018, 1, 021002. [Google Scholar] [CrossRef]
- Martin, R.C.; Kwon, D.; Chalikonda, S.; Sellers, M.; Kotz, E.; Scoggins, C.; McMasters, K.M.; Watkins, K. Treatment of 200 locally advanced (stage III) pancreatic adenocarcinoma patients with irreversible electroporation: Safety and efficacy. Ann. Surg. 2015, 262, 486–494. [Google Scholar] [CrossRef]
- Philips, P.; Hays, D.; Martin, R.C. Irreversible electroporation ablation (IRE) of unresectable soft tissue tumors: Learning curve evaluation in the first 150 patients treated. PLoS ONE 2013, 8, e76260. [Google Scholar] [CrossRef] [PubMed]
- Ansari, D.; Kristoffersson, S.; Andersson, R.; Bergenfeldt, M. The role of irreversible electroporation (IRE) for locally advanced pancreatic cancer: A systematic review of safety and efficacy. Scand. J. Gastroenterol. 2017, 52, 1165–1171. [Google Scholar] [CrossRef] [PubMed]
- Silk, M.T.; Wimmer, T.; Lee, K.S.; Srimathveeravalli, G.; Brown, K.T.; Kingham, P.T.; Fong, Y.; Durack, J.C.; Sofocleous, C.T.; Solomon, S.B. Percutaneous ablation of peribiliary tumors with irreversible electroporation. J. Vasc. Interv. Radiol. 2014, 25, 112–118. [Google Scholar] [CrossRef]
- Dunki-Jacobs, E.; Philips, P.; Martin Ii, R. Evaluation of thermal injury to liver, pancreas and kidney during irreversible electroporation in an in vivo experimental model. J. Br. Surg. 2014, 101, 1113–1121. [Google Scholar] [CrossRef]
- Kurata, K.; Nomura, S.; Takamatsu, H. Three-dimensional analysis of irreversible electroporation: Estimation of thermal and non-thermal damage. Int. J. Heat Mass Transf. 2014, 72, 66–74. [Google Scholar] [CrossRef]
- Wagstaff, P.G.; de Bruin, D.M.; van den Bos, W.; Ingels, A.; van Gemert, M.J.; Zondervan, P.J.; Verdaasdonk, R.M.; van Lienden, K.P.; van Leeuwen, T.G.; de la Rosette, J.J.; et al. Irreversible electroporation of the porcine kidney: Temperature development and distribution. In Urologic Oncology: Seminars and Original Investigations; Elsevier: Amsterdam, The Netherlands, 2015; Volume 33, pp. 168.e1–168.e7. [Google Scholar]
- Agnass, P.; van Veldhuisen, E.; van Gemert, M.J.; van der Geld, C.W.; van Lienden, K.P.; van Gulik, T.M.; Meijerink, M.R.; Besselink, M.G.; Kok, H.P.; Crezee, J. Mathematical modeling of the thermal effects of irreversible electroporation for in vitro, in vivo, and clinical use: A systematic review. Int. J. Hyperth. 2020, 37, 486–505. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, H.J.; Vogel, J.A.; Van Den Bos, W.; Neal, R.E.; Van Lienden, K.P.; Besselink, M.G.; Van Gemert, M.J.; Van Der Geld, C.W.; Meijerink, M.R.; Klaessens, J.H.; et al. The influence of a metal stent on the distribution of thermal energy during irreversible electroporation. PLoS ONE 2016, 11, e0148457. [Google Scholar] [CrossRef] [PubMed]
- Brock, R.M.; Beitel-White, N.; Davalos, R.V.; Allen, I.C. Starting a fire without flame: The induction of cell death and inflammation in electroporation-based tumor ablation strategies. Front. Oncol. 2020, 10, 1235. [Google Scholar] [CrossRef]
- Zhao, J.; Wen, X.; Tian, L.; Li, T.; Xu, C.; Wen, X.; Melancon, M.P.; Gupta, S.; Shen, B.; Peng, W.; et al. Irreversible electroporation reverses resistance to immune checkpoint blockade in pancreatic cancer. Nat. Commun. 2019, 10, 899. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Li, Z.; Han, X.; Zhu, Z.; Zhao, Y.; Liu, Z.; Lv, Y. Irreversible Electroporation: An Emerging Immunomodulatory Therapy on Solid Tumor. Front. Immunol. 2022, 12, 811726. [Google Scholar] [CrossRef] [PubMed]
- Arena, C.B.; Mahajan, R.L.; Nichole Rylander, M.; Davalos, R.V. An experimental and numerical investigation of phase change electrodes for therapeutic irreversible electroporation. J. Biomech. Eng. 2013, 135, 111009. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, T.J.; Bonakdar, M.; Bhonsle, S.; Neal, R.E.; Aardema Jr, C.H.; Robertson, J.L.; Goldberg, S.N.; Davalos, R.V. Effects of internal electrode cooling on irreversible electroporation using a perfused organ model. Int. J. Hyperth. 2018, 35, 44–55. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, T.J.; Lorenzo, M.F.; Zhao, Y.; Neal II, R.E.; Robertson, J.L.; Goldberg, S.N.; Davalos, R.V. Cycled pulsing to mitigate thermal damage for multi-electrode irreversible electroporation therapy. Int. J. Hyperth. 2019, 36, 952–962. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, J.D.; Fesmire, C.C.; Petrella, R.A.; Fogle, C.A.; Xing, L.; Gerber, D.; Sano, M.B. High-frequency irreversible electroporation using 5000-V waveforms to create reproducible 2-and 4-cm ablation zones—A laboratory investigation using mechanically perfused liver. J. Vasc. Interv. Radiol. 2020, 31, 162–168. [Google Scholar] [CrossRef]
- Aycock, K.N.; Campelo, S.N.; Davalos, R.V. A Comparative Modeling Study of Thermal Mitigation Strategies in Irreversible Electroporation Treatments. J. Heat Transf. 2022, 144, 031206. [Google Scholar] [CrossRef] [PubMed]
- Cindrič, H.; Mariappan, P.; Beyer, L.; Wiggermann, P.; Moche, M.; Miklavčič, D.; Kos, B. Retrospective study for validation and improvement of numerical treatment planning of irreversible electroporation ablation for treatment of liver tumors. IEEE Trans. Biomed. Eng. 2021, 68, 3513–3524. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, M.F.; Bhonsle, S.P.; Arena, C.B.; Davalos, R.V. Rapid impedance spectroscopy for monitoring tissue impedance, temperature, and treatment outcome during electroporation-based therapies. IEEE Trans. Biomed. Eng. 2020, 68, 1536–1546. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251. [Google Scholar] [CrossRef] [PubMed]
- IT’IS Database for thermal and electromagnetic parameters of biological tissues, Version 4.0. Available online: https://itis.swiss/virtual-population/tissue-properties/downloads/database-v4-1/ (accessed on 15 August 2022).
- Garcia, P.A.; Davalos, R.V.; Miklavcic, D. A numerical investigation of the electric and thermal cell kill distributions in electroporation-based therapies in tissue. PLoS ONE 2014, 9, e103083. [Google Scholar] [CrossRef]
- Mohammadi, A.; Bianchi, L.; Asadi, S.; Saccomandi, P. Measurement of ex vivo liver, brain and pancreas thermal properties as function of temperature. Sensors 2021, 21, 4236. [Google Scholar] [CrossRef] [PubMed]
- Popiel, C.; Wojtkowiak, J. Simple formulas for thermophysical properties of liquid water for heat transfer calculations (from 0 C to 150 C). Heat Transf. Eng. 1998, 19, 87–101. [Google Scholar] [CrossRef]
- Ngo, I.L.; Jeon, S.; Byon, C. Thermal conductivity of transparent and flexible polymers containing fillers: A literature review. Int. J. Heat Mass Transf. 2016, 98, 219–226. [Google Scholar] [CrossRef]
- Castellví, Q.; Mercadal, B.; Ivorra, A. Assessment of electroporation by electrical impedance methods. Handb. Electroporation 2016, 67, 1–20. [Google Scholar]
- Ivorra, A.; Rubinsky, B. In vivo electrical impedance measurements during and after electroporation of rat liver. Bioelectrochemistry 2007, 70, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Dean, D.; Ramanathan, T.; Machado, D.; Sundararajan, R. Electrical impedance spectroscopy study of biological tissues. J. Electrost. 2008, 66, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Schwan, H.P. Electrical properties of tissue and cell suspensions. In Advances in Biological and Medical Physics; Elsevier: Amsterdam, The Netherlands, 1957; Volume 5, pp. 147–209. [Google Scholar]
- Voyer, D.; Silve, A.; Mir, L.M.; Scorretti, R.; Poignard, C. Dynamical modeling of tissue electroporation. Bioelectrochemistry 2018, 119, 98–110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jamaludin, I.; Wahab, N.; Khalid, N.; Sahlan, S.; Ibrahim, Z.; Rahmat, M.F. N4SID and MOESP subspace identification methods. In Proceedings of the 2013 IEEE 9th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 8–10 March 2013; pp. 140–145. [Google Scholar]
- Asada, H. Subspace Methods for System Identification: Realization; Department of Mechanical Engineering MIT: Cambridge, MA, USA, 2020. [Google Scholar]







| Material | Parameter | Value | Units | Ref |
|---|---|---|---|---|
| Agar | Density, Specific heat, cp Thermal conductivity, k Temperature coefficient, | 998 4182 0.598 2 | kg/m3 J/(kg·K) W/(m·K) %/C | [36] [36] [36] [36] |
| Insulation | Density, Specific heat, cp Thermal conductivity, k Electrical conductivity, | 2329 700 0.2 1 × 10−12 | kg/m3 J/(kg·K) W/(m·K) S/m | [26] [26] [37] [26] |
| Stainless Steel | Density, Specific heat, cp Thermal conductivity, k Electrical conductivity, | 7900 500 15 2.22 × 106 | kg/m3 J/(kg·K) W/(m·K) S/m | [26] [26] [26] [26] |
| Temperature Distance | HV-HC | LV-LC | HV-LC | LV-HC | |
|---|---|---|---|---|---|
| Fit Accuracy (%) | T | 95.8 | 88.4 | 90.7 | 93.7 |
| T | 93.2 | 58.9 | 90.0 | 90.9 | |
| Maximum Absolute Error (C) | T | 1.45 | 0.06 | 0.30 | 0.19 |
| T | 0.52 | 0.35 | 0.31 | 0.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campelo, S.N.; Jacobs, E.J., IV; Aycock, K.N.; Davalos, R.V. Real-Time Temperature Rise Estimation during Irreversible Electroporation Treatment through State-Space Modeling. Bioengineering 2022, 9, 499. https://doi.org/10.3390/bioengineering9100499
Campelo SN, Jacobs EJ IV, Aycock KN, Davalos RV. Real-Time Temperature Rise Estimation during Irreversible Electroporation Treatment through State-Space Modeling. Bioengineering. 2022; 9(10):499. https://doi.org/10.3390/bioengineering9100499
Chicago/Turabian StyleCampelo, Sabrina N., Edward J. Jacobs, IV, Kenneth N. Aycock, and Rafael V. Davalos. 2022. "Real-Time Temperature Rise Estimation during Irreversible Electroporation Treatment through State-Space Modeling" Bioengineering 9, no. 10: 499. https://doi.org/10.3390/bioengineering9100499
APA StyleCampelo, S. N., Jacobs, E. J., IV, Aycock, K. N., & Davalos, R. V. (2022). Real-Time Temperature Rise Estimation during Irreversible Electroporation Treatment through State-Space Modeling. Bioengineering, 9(10), 499. https://doi.org/10.3390/bioengineering9100499