Thermal Conductivity of Detonation Nanodiamond Hydrogels and Hydrosols by Direct Heat Flux Measurements
Abstract
:1. Introduction
2. Results
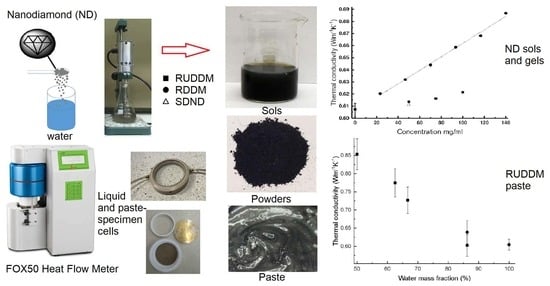
2.1. Nanodiamond Hydrosols
2.2. Nanodiamond Gels and Pastes
3. Discussion
4. Conclusions
5. Materials and Methods
5.1. FOX 50 Heat Flow Meter
5.2. Other Equipment
5.3. Samples
5.4. Reagents and Solvents
5.5. Sample Preparation Procedures
5.5.1. Preparation of Sols and Gels
5.5.2. Preparation of RUDDM Pastes
5.6. Determination of Thermal Conductivity
5.7. Heat Flux Measurements
5.7.1. Two-Spacer Calibration with Pyrex
5.7.2. Measurements in a Liquid Cell
5.7.3. Measurements in the Paste-Specimen Cell
5.8. Rheological Measurements
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calibration of the Heat Flux Cell for Liquids
Appendix A1. Plate Temperature Difference



Appendix A2. Solvent
| Solvent | kexp ± 0.005 | kref [63] |
|---|---|---|
| Water | 0.526 | 0.607 |
| Methanol | 0.194 | 0.202 |
| Ethanol | 0.158 | 0.167 |
| Ethylene glycol | 0.233 | 0.254 |
| N-methyl-2-pyrrolidone | 0.157 | 0.167 |

Appendix A3. Sample Thickness
Appendix B. Silicon Oxide Sols

| AM | ,% | 1.6 | 3.2 | 8.1 | 16.1 | , R2 = 0.999 |
| k, W m−1 K−1 | 0.615 | 0.621 (2) | 0.646 (6) | 0.682 (12) | ||
| SM-30 | ,% | 1.6 | 3.2 | 8.1 | 16.1 | , R2 = 0.998 |
| k, W m−1 K−1 | 0.611 | 0.619 (2) | 0.636 (5) | 0.672 (10) | ||
| TMA | ,% | 1.9 | 3.8 | 9.4 | 18.8 | , R2 = 0.990 |
| k, W m−1 K−1 | 0.621 | 0.626 (3) | 0.656 (8) | 0.688 (13) | ||
| HS-40 | ,% | 2.3 | 4.6 | 11.5 | 23 | , R2 = 0.993 |
| k, W m−1 K−1 | 0.619 | 0.638 (5) | 0.665 (9) | 0.714 (18) | ||
| CL-X | ,% | 2.7 | 5.4 | 13.4 | 26.9 | , R2 = 0.998 |
| k, W m−1 K−1 | 0.616 | 0.628 (3) | 0.657 (8) | 0.703 (16) | ||
| TM-50 | ,% | 3.1 | 6.2 | 15.4 | 30.9 | , R2 = 0.999 |
| k, W m−1 K−1 | 0.622 | 0.636 (5) | 0.681 (12) | 0.755 (24) |

References
- Dolmatov, V.Y. Detonation-synthesis nanodiamonds: Synthesis, structure, properties and applications. Russ. Chem. Rev. 2007, 76, 339–360. [Google Scholar] [CrossRef]
- Chernysheva, M.G.; Popov, A.G.; Tashlitsky, V.N.; Badun, G.A. Cationic surfactant coating nanodiamonds: Adsorption and peculiarities. Colloids Surf. Physicochem. Eng. Aspects 2019, 565, 25–29. [Google Scholar] [CrossRef]
- Shenderova, O.A.; Gruen, D.M. Ultrananocrystalline Diamond, 2nd ed.; Shenderova, O.A., Ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zhang, K.; Zhao, Q.; Qin, S.; Fu, Y.; Liu, R.; Zhi, J.; Shan, C. Nanodiamonds conjugated upconversion nanoparticles for bio-imaging and drug delivery. J. Colloid Interface Sci. 2019, 537, 316–324. [Google Scholar] [CrossRef]
- Qin, S.-R.; Zhao, Q.; Cheng, Z.-G.; Zhang, D.-X.; Zhang, K.-K.; Su, L.-X.; Fan, H.-J.; Wang, Y.-H.; Shan, C.-X. Rare earth-functionalized nanodiamonds for dual-modal imaging and drug delivery. Diamond Relat. Mater. 2019, 91, 173–182. [Google Scholar] [CrossRef]
- Mochalin, V.N.; Pentecost, A.; Li, X.M.; Neitzel, I.; Nelson, M.; Wei, C.; He, T.; Guo, F.; Gogotsi, Y. Adsorption of drugs on nanodiamond: Toward development of a drug delivery platform. Mol. Pharm. 2013, 10, 3728–3735. [Google Scholar] [CrossRef]
- Mochalin, V.N.; Shenderova, O.; Ho, D.; Gogotsi, Y. The properties and applications of nanodiamonds. Nat. Nanotechnol. 2011, 7, 11–23. [Google Scholar] [CrossRef]
- Buchatskaya, Y.; Romanchuk, A.; Yakovlev, R.; Shiryaev, A.; Kulakova, I.; Kalmykov, S. Sorption of actinides onto nanodiamonds. Radiochim. Acta 2015, 103, 205–211. [Google Scholar] [CrossRef]
- Stehlik, S.; Varga, M.; Ledinsky, M.; Jirasek, V.; Artemenko, A.; Kozak, H.; Ondic, L.; Skakalova, V.; Argentero, G.; Pennycook, T.; et al. Size and purity control of HPHT Nanodiamonds down to 1 nm. J. Phys. Chem. C Nanomater. Interfaces 2015, 119, 27708–27720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balandin, A.A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Usoltseva, L.O.; Korobov, M.V.; Proskurnin, M.A. Photothermal spectroscopy: A promising tool for nanofluids. J. Appl. Phys. 2020, 128, 190901. [Google Scholar] [CrossRef]
- Volkov, D.S.; Proskurnin, M.A.; Korobov, M.V. Elemental analysis of nanodiamonds by inductively-coupled plasma atomic emission spectroscopy. Carbon 2014, 74, 1–13. [Google Scholar] [CrossRef]
- Huang, H.; Pierstorff, E.; Osawa, E.; Ho, D. Active nanodiamond hydrogels for chemotherapeutic delivery. Nano Lett. 2007, 7, 3305–3314. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Pierstorff, E.; Osawa, E.; Ho, D. Protein-mediated assembly of nanodiamond hydrogels into a biocompatible and biofunctional multilayer nanofilm. ACS Nano 2008, 2, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Proskurnin, M.A.; Usoltseva, L.O.; Volkov, D.S.; Nedosekin, D.A.; Korobov, M.V.; Zharov, V.P. Photothermal and heat-transfer properties of aqueous detonation nanodiamonds by photothermal microscopy and transient spectroscopy. J. Phys. Chem. C 2021, 125, 7808–7823. [Google Scholar] [CrossRef]
- Qiu, L.; Zhu, N.; Feng, Y.; Michaelides, E.E.; Żyła, G.; Jing, D.; Zhang, X.; Norris, P.M.; Markides, C.N.; Mahian, O. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys. Rep. 2020, 843, 1–81. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Nimo, J.; Pastoriza-Gallego, M.; Piñeiro, M.; Legido, J.; Lugo, L. Thermal conductivity of dry anatase and rutile nano-powders and ethylene and propylene glycol-based TiO2 nanofluids. J. Chem. Thermodyn. 2015, 83, 67–76. [Google Scholar] [CrossRef]
- Shvidchenko, A.V.; Eidelman, E.D.; Vul, A.Y.; Kuznetsov, N.M.; Stolyarova, D.Y.; Belousov, S.I.; Chvalun, S.N. Colloids of detonation nanodiamond particles for advanced applications. Adv. Colloid Interface Sci. 2019, 268, 64–81. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, N.M.; Belousov, S.I.; Bakirov, A.V.; Chvalun, S.N.; Kamyshinsky, R.A.; Mikhutkin, A.A.; Vasiliev, A.L.; Tolstoy, P.M.; Mazur, A.S.; Eidelman, E.D. Unique rheological behavior of detonation nanodiamond hydrosols: The nature of sol-gel transition. Carbon 2020, 161, 486–494. [Google Scholar] [CrossRef]
- Mikheev, I.V.; Pirogova, M.O.; Usoltseva, L.O.; Uzhel, A.S.; Bolotnik, T.A.; Kareev, I.E.; Bubnov, V.P.; Lukonina, N.S.; Volkov, D.S.; Goryunkov, A.A.; et al. Green and rapid preparation of long-term stable aqueous dispersions of fullerenes and endohedral fullerenes: The pros and cons of an ultrasonic probe. Ultrason. Sonochem. 2021, 73, 105533. [Google Scholar] [CrossRef] [PubMed]
- Tomchuk, O.V.; Avdeev, M.V.; Aleksenskii, A.E.; Vul, A.Y.; Ivankov, O.I.; Ryukhtin, V.V.; Füzi, J.; Garamus, V.M.; Bulavin, L.A. Sol-gel transition in nanodiamond aqueous dispersions by small-angle scattering. J. Phys. Chem. C 2019, 123, 18028–18036. [Google Scholar] [CrossRef]
- Vul, A.Y.; Eidelman, E.D.; Aleksenskiy, A.E.; Shvidchenko, A.V.; Dideikin, A.T.; Yuferev, V.S.; Lebedev, V.T.; Kul’velis, Y.V.; Avdeev, M.V. Transition sol-gel in nanodiamond hydrosols. Carbon 2017, 114, 242–249. [Google Scholar] [CrossRef]
- Kuznetsov, N.M.; Belousov, S.I.; Stolyarova, D.Y.; Bakirov, A.V.; Chvalun, S.N.; Shvidchenko, A.V.; Eidelman, E.D.; Vul, A.Y. Effect of diamond nanoparticle chains on rheological properties of hydrosol. Diamond Relat. Mater. 2018, 83, 141–145. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Usoltseva, L.O.; Volkov, D.S.; Avramenko, N.V.; Korobov, M.V.; Proskurnin, M.A. Nanodiamond aqueous dispersions as potential nanofluids: The determination of properties by thermal lensing and other techniques. Nanosyst. Phys. Chem. Math. 2018, 9, 17–20. [Google Scholar] [CrossRef] [Green Version]
- Prasher, R.; Song, D.; Wang, J.; Phelan, P. Measurements of nanofluid viscosity and its implications for thermal applications. Appl. Phys. Lett. 2006, 89, 133108. [Google Scholar] [CrossRef]
- Eapen, J.; Williams, W.C.; Buongiorno, J.; Hu, L.W.; Yip, S.; Rusconi, R.; Piazza, R. Mean-field versus microconvection effects in nanofluid thermal conduction. Phys. Rev. Lett. 2007, 99, 095901. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Yu, W.; Singh, D.; Cookson, D.; Routbort, J. Application of SAXS to the study of particle-size-dependent thermal conductivity in silica nanofluids. J. Nanoparticle Res. 2008, 10, 1109–1114. [Google Scholar] [CrossRef]
- Buongiorno, J.; Venerus, D.C.; Prabhat, N.; McKrell, T.; Townsend, J.; Christianson, R.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.-w.; Alvarado, J.L.; et al. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 2009, 106, 094312. [Google Scholar] [CrossRef] [Green Version]
- Laun, H.M. Rheological properties of aqueous polymer dispersions. Angew. Makromol. Chem. 1984, 123, 335–359. [Google Scholar] [CrossRef]
- Comet, M.; Pichot, V.; Schnell, F.; Spitzer, D. Oxidation of detonation nanodiamonds in a reactive formulation. Diamond Relat. Mater. 2014, 47, 35–39. [Google Scholar] [CrossRef]
- Yeganeh, M.; Shahtahmasebi, N.; Kompany, A.; Goharshadi, E.; Youssefi, A.; Šiller, L. Volume fraction and temperature variations of the effective thermal conductivity of nanodiamond fluids in deionized water. Int. J. Heat Mass Transf. 2010, 53, 3186–3192. [Google Scholar] [CrossRef]
- Yu, Q.; Kim, Y.J.; Ma, H. Nanofluids with plasma treated diamond nanoparticles. Appl. Phys. Lett. 2008, 92, 103111. [Google Scholar] [CrossRef]
- Sundar, L.S.; Hortiguela, M.J.; Singh, M.K.; Sousa, A.C.M. Thermal conductivity and viscosity of water based nanodiamond (ND) nanofluids: An experimental study. Int. Commun. Heat Mass Transf. 2016, 76, 245–255. [Google Scholar] [CrossRef]
- Mashali, F.; Languri, E.; Mirshekari, G.; Davidson, J.; Kerns, D. Nanodiamond nanofluid microstructural and thermo-electrical characterization. Int. Commun. Heat Mass Transf. 2019, 101, 82–88. [Google Scholar] [CrossRef]
- Guzei, D.; Minakov, A.; Rudyak, V.Y. On efficiency of convective heat transfer of nanofluids in laminar flow regime. Int. J. Heat Mass Transf. 2019, 139, 180–192. [Google Scholar] [CrossRef]
- Xie, H.; Yu, W.; Li, Y. Thermal performance enhancement in nanofluids containing diamond nanoparticles. J. Phys. D Appl. Phys. 2009, 42, 095413. [Google Scholar] [CrossRef]
- Sundar, L.S.; Singh, M.K.; Sousa, A.C. Experimental thermal conductivity and viscosity of nanodiamond-based propylene glycol and water mixtures. Diamond Relat. Mater. 2016, 69, 49–60. [Google Scholar] [CrossRef]
- Xie, H.; Yu, W.; Li, Y.; Chen, L. Discussion on the thermal conductivity enhancement of nanofluids. Nanoscale Res. Lett. 2011, 6, 124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taha-Tijerina, J.J.; Narayanan, T.N.; Tiwary, C.S.; Lozano, K.; Chipara, M.; Ajayan, P.M. Nanodiamond-based thermal fluids. ACS Appl. Mater. Interfaces 2014, 6, 4778–4785. [Google Scholar] [CrossRef]
- Kidalov, S.; Shakhov, F.; Vul, A.Y. Thermal conductivity of sintered nanodiamonds and microdiamonds. Diamond Relat. Mater. 2008, 17, 844–847. [Google Scholar] [CrossRef]
- Matsubara, H.; Kikugawa, G.; Bessho, T.; Ohara, T. Evaluation of thermal conductivity and its structural dependence of a single nanodiamond using molecular dynamics simulation. Diamond Relat. Mater. 2020, 102, 107669. [Google Scholar] [CrossRef]
- Khvesyuk, V.I.; Skryabin, A.S. Heat conduction in nanostructures. High Temp. 2017, 55, 434–456. [Google Scholar] [CrossRef]
- Volchenko, T.S.; Yalovets, A.P. Calculation of the effective thermal conductivity of powders formed by spherical particles in a gaseous atmosphere. Tech. Phys. 2016, 61, 324–336. [Google Scholar] [CrossRef]
- Pujula, M.; Sánchez-Rodríguez, D.; Lopez-Olmedo, J.P.; Farjas, J.; Roura, P. Measuring thermal conductivity of powders with differential scanning calorimetry. J. Therm. Anal. Calorim. 2016, 125, 571–577. [Google Scholar] [CrossRef] [Green Version]
- Torii, S.; Yang, W.-J. Heat transfer augmentation of aqueous suspensions of nanodiamonds in turbulent pipe flow. J. Heat Transf. 2009, 131, 043203. [Google Scholar] [CrossRef]
- Torii, S. Experimental study on thermal transport phenomenon of nanofluids as working fluid in heat exchanger. Int. J. Air-Cond. Refrig. 2014, 22, 1450005. [Google Scholar] [CrossRef]
- Pryazhnikov, M.; Minakov, A.; Rudyak, V.Y.; Guzei, D. Thermal conductivity measurements of nanofluids. Int. J. Heat Mass Transf. 2017, 104, 1275–1282. [Google Scholar] [CrossRef] [Green Version]
- Jang, S.P.; Choi, S.U. Cooling performance of a microchannel heat sink with nanofluids. Appl. Therm. Eng. 2006, 26, 2457–2463. [Google Scholar] [CrossRef]
- Kidalov, S.V.; Shakhov, F.M.; Vul, A.Y. Thermal conductivity of nanocomposites based on diamonds and nanodiamonds. Diamond Relat. Mater. 2007, 16, 2063–2066. [Google Scholar] [CrossRef]
- Bialkowski, S.E.; Astrath, N.G.C.; Proskurnin, M.A. Photothermal Spectroscopy Methods; Wiley: Hoboken, NJ, USA, 2019; p. 512. [Google Scholar]
- Mikheev, I.V.; Usoltseva, L.O.; Ivshukov, D.A.; Volkov, D.S.; Korobov, M.V.; Proskurnin, M.A. Approach to the Assessment of size-dependent thermal properties of disperse solutions: Time-resolved photothermal lensing of aqueous pristine fullerenes C60 and C70. J. Phys. Chem. C 2016, 120, 28270–28287. [Google Scholar] [CrossRef]
- Meilakhs, A.; Aleksenskii, A. Diffusion of overheated and overcooled particles as a mechanism of thermal conductivity in nanofluids. JETP Lett. 2020, 111, 338–342. [Google Scholar] [CrossRef]
- Ge, Z.; Cahill, D.G.; Braun, P.V. Thermal conductance of hydrophilic and hydrophobic interfaces. Phys. Rev. Lett. 2006, 96, 186101. [Google Scholar] [CrossRef] [PubMed]
- Alexeev, D.; Chen, J.; Walther, J.H.; Giapis, K.P.; Angelikopoulos, P.; Koumoutsakos, P. Kapitza resistance between few-layer graphene and water: Liquid layering effects. Nano Lett. 2015, 15, 5744–5749. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Ma, R.; Zhang, T.; Luo, T. Origin of hydrophilic surface functionalization-induced thermal conductance enhancement across solid-water interfaces. ACS Appl. Mater. Interfaces 2018, 10, 28159–28165. [Google Scholar] [CrossRef] [PubMed]
- Rajabpour, A.; Seif, R.; Arabha, S.; Heyhat, M.M.; Merabia, S.; Hassanali, A. Thermal transport at a nanoparticle-water interface: A molecular dynamics and continuum modeling study. J. Chem. Phys. 2019, 150, 114701. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Yang, M.; Liu, B.; Xu, M.; Zhang, T.; Zhuang, B.; Ding, D.; Huai, X.; Zhang, H. Enhanced thermal conductance at the graphene–water interface based on functionalized alkane chains. RSC Adv. 2019, 9, 4563–4570. [Google Scholar] [CrossRef] [Green Version]
- Jabbari, F.; Rajabpour, A.; Saedodin, S.; Wongwises, S. Effect of water/carbon interaction strength on interfacial thermal resistance and the surrounding molecular nanolayer of CNT and graphene flake. J. Mol. Liq. 2019, 282, 197–204. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Wang, L. Review of heat conduction in nanofluids. J. Heat Transf. 2011, 133, 040801. [Google Scholar] [CrossRef]
- Volkov, D.S.; Krivoshein, P.K.; Mikheev, I.V.; Proskurnin, M.A. Pristine detonation nanodiamonds as regenerable adsorbents for metal cations. Diamond Relat. Mater. 2020, 110, 108121. [Google Scholar] [CrossRef]
- Usoltseva, L.O.; Volkov, D.S.; Nedosekin, D.A.; Korobov, M.V.; Proskurnin, M.A.; Zharov, V.P. Absorption spectra of nanodiamond aqueous dispersions by optical absorption and optoacoustic spectroscopies. Photoacoustics 2018, 12, 55–66. [Google Scholar] [CrossRef] [PubMed]
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 96th ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Tavman, I.; Turgut, A.; Chirtoc, M.; Schuchmann, H.; Tavman, S. Experimental investigation of viscosity and thermal conductivity of suspensions containing nanosized ceramic particles. Arch. Mater. Sci. 2008, 34, 99–104. [Google Scholar]
- Kang, H.U.; Kim, S.H.; Oh, J.M. Estimation of thermal conductivity of nanofluid using experimental effective particle volume. Exp. Heat Transf. 2006, 19, 181–191. [Google Scholar] [CrossRef]
- Yan, S.; Wang, F.; Shi, Z.; Tian, R. Heat transfer property of SiO2/water nanofluid flow inside solar collector vacuum tubes. Appl. Therm. Eng. 2017, 118, 385–391. [Google Scholar] [CrossRef]
- Moldoveanu, G.M.; Huminic, G.; Minea, A.A.; Huminic, A. Experimental study on thermal conductivity of stabilized Al2O3 and SiO2 nanofluids and their hybrid. Int. J. Heat Mass Transf. 2018, 127, 450–457. [Google Scholar] [CrossRef]
- Jahanshahi, M.; Hosseinizadeh, S.; Alipanah, M.; Dehghani, A.; Vakilinejad, G. Numerical simulation of free convection based on experimental measured conductivity in a square cavity using Water/SiO2 nanofluid. Int. Commun. Heat Mass Transf. 2010, 37, 687–694. [Google Scholar] [CrossRef]
- Palacios, A.; Cong, L.; Navarro, M.E.; Ding, Y.; Barreneche, C. Thermal conductivity measurement techniques for characterizing thermal energy storage materials—A review. Renew. Sustain. Energy Rev. 2019, 108, 32–52. [Google Scholar] [CrossRef]
- Antoniadis, K.D.; Tertsinidou, G.J.; Assael, M.J.; Wakeham, W.A. Necessary conditions for accurate, transient hot-wire measurements of the apparent thermal conductivity of nanofluids are seldom satisfied. Int. J. Thermophys. 2016, 37, 78. [Google Scholar] [CrossRef]










| RDDM | c, mg mL−1 | 23 | 47 | 70 | 93 | 117 | 140 |
| c,% v/v | 0.7 | 1.4 | 2.0 | 2.7 | 3.4 | 4.1 | |
| k, W m−1 K−1 | 0.620 (2%) | 0.632 (4%) | 0.644 (6%) | 0.659 (8%) | 0.668 (10%) | 0.687 (13%) | |
| RUDDM | c, mg mL−1 | 50 | 75 | 100 | |||
| c,% v/v | 1.7 | 2.4 | 3.5 | ||||
| k, W m−1 K−1 | 0.613 | 0.616 | 0.621 (2%) | ||||
| SDND | c, mg mL−1 | 50 | |||||
| c,% v/v | 1.4 | ||||||
| k, W m−1 K−1 | 0.611 |
| Measurement | T.E. | S.E. | P.E.% | min N.B. | C.B. | ΔT |
|---|---|---|---|---|---|---|
| Two-thickness calibration | 0.5 °C | 200 µV | 2 | 16 | 6 | 20 °C |
| Liquid cell test | 0.5 °C | 200 µV | 2 | 15 | 5 | 20 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usoltseva, L.O.; Volkov, D.S.; Karpushkin, E.A.; Korobov, M.V.; Proskurnin, M.A. Thermal Conductivity of Detonation Nanodiamond Hydrogels and Hydrosols by Direct Heat Flux Measurements. Gels 2021, 7, 248. https://doi.org/10.3390/gels7040248
Usoltseva LO, Volkov DS, Karpushkin EA, Korobov MV, Proskurnin MA. Thermal Conductivity of Detonation Nanodiamond Hydrogels and Hydrosols by Direct Heat Flux Measurements. Gels. 2021; 7(4):248. https://doi.org/10.3390/gels7040248
Chicago/Turabian StyleUsoltseva, Liliya O., Dmitry S. Volkov, Evgeny A. Karpushkin, Mikhail V. Korobov, and Mikhail A. Proskurnin. 2021. "Thermal Conductivity of Detonation Nanodiamond Hydrogels and Hydrosols by Direct Heat Flux Measurements" Gels 7, no. 4: 248. https://doi.org/10.3390/gels7040248
APA StyleUsoltseva, L. O., Volkov, D. S., Karpushkin, E. A., Korobov, M. V., & Proskurnin, M. A. (2021). Thermal Conductivity of Detonation Nanodiamond Hydrogels and Hydrosols by Direct Heat Flux Measurements. Gels, 7(4), 248. https://doi.org/10.3390/gels7040248