A Light Scattering Investigation of Enzymatic Gelation in Self-Assembling Peptides
Abstract
:1. Introduction
2. Results and Discussion
2.1. pH Evolution in the Urea–Urease Reaction: Optimizing Parameters to Obtain Homogeneous Gels
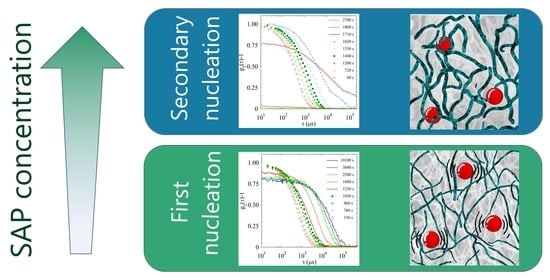
2.2. Light Scattering Study of the SAPs’ Aggregation Kinetics
2.2.1. Sample H
2.2.2. Sample L
2.2.3. Comparison of Samples’ Dynamics
2.3. Light Scattering Study of the SAPs Solution Seeded with Nanoparticles
2.3.1. Sample H
2.3.2. Sample L
2.4. Discussion
3. Conclusions
4. Materials and Methods
4.1. SAP Sample Preparation
4.2. Optical Methods: Dynamic Light Scattering and Photon Correlation Imaging
4.3. pH Measurement
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAP | Self-assembling peptides |
| ECM | Extracellular matrix |
| GdL | Glucono--lactone |
| CD | Circular dichroism |
| FTIR | Fourier-transform infrared spectroscopy |
| Fmoc | 9-Fluorenylmethyloxycarbonyl |
| Tfa | Trifluoroacetate |
| HPLC | High-performance liquid chromatography |
| LC-MS | Liquid chromatography–mass spectroscopy |
| DLS | Dynamic light scattering |
| PCI | Photon correlation imaging |
| ICF | Intensity correlation function |
References
- Carlini, A.S.; Adamiak, L.; Gianneschi, N.C. Biosynthetic polymers as functional materials. Macromolecules 2016, 49, 4379–4394. [Google Scholar] [CrossRef] [PubMed]
- Panja, S.; Adams, D.J. Urea-Urease Reaction in Controlling Properties of Supramolecular Hydrogels: Pros and Cons. Chem.-Eur. J. 2021, 27, 8928–8939. [Google Scholar] [CrossRef] [PubMed]
- Estroff, L.A.; Hamilton, A.D. Water gelation by small organic molecules. Chem. Rev. 2004, 104, 1201–1218. [Google Scholar] [CrossRef]
- Schweitzer-Stenner, R.; Alvarez, N.J. Short peptides as tunable, switchable, and strong gelators. J. Phys. Chem. B 2021, 125, 6760–6775. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yang, Z. Short-peptide-based molecular hydrogels: Novel gelation strategies and applications for tissue engineering and drug delivery. Nanoscale 2012, 4, 5259–5267. [Google Scholar] [CrossRef]
- Sutton, S.; Campbell, N.L.; Cooper, A.I.; Kirkland, M.; Frith, W.J.; Adams, D.J. Controlled release from modified amino acid hydrogels governed by molecular size or network dynamics. Langmuir 2009, 25, 10285–10291. [Google Scholar] [CrossRef] [PubMed]
- Naskar, J.; Palui, G.; Banerjee, A. Tetrapeptide-based hydrogels: For encapsulation and slow release of an anticancer drug at physiological pH. J. Phys. Chem. B 2009, 113, 11787–11792. [Google Scholar] [CrossRef]
- Raspa, A.; Carminati, L.; Pugliese, R.; Fontana, F.; Gelain, F. Self-assembling peptide hydrogels for the stabilization and sustained release of active Chondroitinase ABC in vitro and in spinal cord injuries. J. Control. Release 2021, 330, 1208–1219. [Google Scholar] [CrossRef]
- Sangeetha, N.M.; Maitra, U. Supramolecular gels: Functions and uses. Chem. Soc. Rev. 2005, 34, 821–836. [Google Scholar] [CrossRef]
- Genové, E.; Shen, C.; Zhang, S.; Semino, C.E. The effect of functionalized self-assembling peptide scaffolds on human aortic endothelial cell function. Biomaterials 2005, 26, 3341–3351. [Google Scholar] [CrossRef]
- Gelain, F.; Luo, Z.; Zhang, S. Self-assembling peptide EAK16 and RADA16 nanofiber scaffold hydrogel. Chem. Rev. 2020, 120, 13434–13460. [Google Scholar] [CrossRef] [PubMed]
- Loo, Y.; Wan, A.C.; Hauser, C.A.; Lane, E.B.; Benny, P. Xeno-free self-assembling peptide scaffolds for building 3D organotypic skin cultures. FASEB BioAdvances 2022, 4, 631–637. [Google Scholar] [CrossRef] [PubMed]
- Gelain, F.; Bottai, D.; Vescovi, A.; Zhang, S. Designer self-assembling peptide nanofiber scaffolds for adult mouse neural stem cell 3-dimensional cultures. PLoS ONE 2006, 1, e119. [Google Scholar] [CrossRef] [PubMed]
- Gelain, F.; Luo, Z.; Rioult, M.; Zhang, S. Self-assembling peptide scaffolds in the clinic. NPJ Regen. Med. 2021, 6, 9. [Google Scholar] [CrossRef] [PubMed]
- Fu, K.; Wu, H.; Su, Z. Self-assembling peptide-based hydrogels: Fabrication, properties, and applications. Biotechnol. Adv. 2021, 49, 107752. [Google Scholar] [CrossRef] [PubMed]
- Pugliese, R.; Gelain, F. Peptidic biomaterials: From self-assembling to regenerative medicine. Trends Biotechnol. 2017, 35, 145–158. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Z.; Adams, D.J. Controlling peptidebased hydrogelation. Mater. Today 2012, 15, 500–507. [Google Scholar] [CrossRef]
- Amdursky, N.; Orbach, R.; Gazit, E.; Huppert, D. Probing the inner cavities of hydrogels by proton diffusion. J. Phys. Chem. C 2009, 113, 19500–19505. [Google Scholar] [CrossRef]
- Diaferia, C.; Rosa, E.; Morelli, G.; Accardo, A. Fmoc-diphenylalanine hydrogels: Optimization of preparation methods and structural insights. Pharmaceuticals 2022, 15, 1048. [Google Scholar] [CrossRef]
- Diaferia, C.; Rosa, E.; Gallo, E.; Morelli, G.; Accardo, A. Differently N-Capped Analogues of Fmoc-FF. Chem.-Eur. J. 2023, e202300661. [Google Scholar] [CrossRef]
- Majumder, L.; Chatterjee, M.; Bera, K.; Maiti, N.C.; Banerji, B. Solvent-assisted tyrosine-based dipeptide forms low-molecular weight gel: Preparation and its potential use in dye removal and oil spillage separation from water. ACS Omega 2019, 4, 14411–14419. [Google Scholar] [CrossRef]
- Li, X.; Gao, Y.; Kuang, Y.; Xu, B. Enzymatic formation of a photoresponsive supramolecular hydrogel. Chem. Commun. 2010, 46, 5364–5366. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Mao, H.; Tong, S.c.; Liu, C.; Yan, R.; Zhao, L.; Zhu, L.; Bao, C. A Facile and Versatile Approach to Construct Photoactivated Peptide Hydrogels by Regulating Electrostatic Repulsion. ACS Nano 2023, 17, 5536–5547. [Google Scholar] [CrossRef]
- Vegners, R.; Shestakova, I.; Kalvinsh, I.; Ezzell, R.M.; Janmey, P.A. Use of a gel-forming dipeptide derivative as a carrier for antigen presentation. J. Pept. Sci. Off. Publ. Eur. Pept. Soc. 1995, 1, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Xing, H.; Rodger, A.; Comer, J.; Picco, A.S.; Huck-Iriart, C.; Ezell, E.L.; Conda-Sheridan, M. Urea-modified self-assembling peptide amphiphiles that form well-defined nanostructures and hydrogels for biomedical applications. ACS Appl. Bio Mater. 2022, 5, 4599–4610. [Google Scholar] [CrossRef] [PubMed]
- de Loos, M.; Friggeri, A.; van Esch, J.; Kellogg, R.M.; Feringa, B.L. Cyclohexane bis-urea compounds for the gelation of water and aqueous solutions. Org. Biomol. Chem. 2005, 3, 1631–1639. [Google Scholar] [CrossRef] [PubMed]
- Helen, W.; De Leonardis, P.; Ulijn, R.V.; Gough, J.; Tirelli, N. Mechanosensitive peptide gelation: Mode of agitation controls mechanical properties and nano-scale morphology. Soft Matter 2011, 7, 1732–1740. [Google Scholar] [CrossRef]
- Panja, S.; Adams, D.J. Maintaining homogeneity during a sol–gel transition by an autocatalytic enzyme reaction. Chem. Commun. 2019, 55, 47–50. [Google Scholar] [CrossRef]
- Reddy, S.M.M.; Shanmugam, G.; Duraipandy, N.; Kiran, M.S.; Mandal, A.B. An additional fluorenylmethoxycarbonyl (Fmoc) moiety in di-Fmoc-functionalized L-lysine induces pH-controlled ambidextrous gelation with significant advantages. Soft Matter 2015, 11, 8126–8140. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, H.; Yang, Z.; Xu, B. Supramolecular hydrogels respond to ligand- receptor interaction. J. Am. Chem. Soc. 2003, 125, 13680–13681. [Google Scholar] [CrossRef]
- Mahler, A.; Reches, M.; Rechter, M.; Cohen, S.; Gazit, E. Rigid, self-assembled hydrogel composed of a modified aromatic dipeptide. Adv. Mater. 2006, 18, 1365–1370. [Google Scholar] [CrossRef]
- Adams, D.J.; Butler, M.F.; Frith, W.J.; Kirkland, M.; Mullen, L.; Sanderson, P. A new method for maintaining homogeneity during liquid–hydrogel transitions using low molecular weight hydrogelators. Soft Matter 2009, 5, 1856–1862. [Google Scholar] [CrossRef]
- Pocker, Y.; Green, E. Hydrolysis of D-glucono-. delta.-lactone. I. General acid-base catalysis, solvent deuterium isotope effects, and transition state characterization. J. Am. Chem. Soc. 1973, 95, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Braun, G.A.; Ary, B.E.; Dear, A.J.; Rohn, M.C.; Payson, A.M.; Lee, D.S.; Parry, R.C.; Friedman, C.; Knowles, T.P.; Linse, S.; et al. On the mechanism of self-assembly by a hydrogel-forming peptide. Biomacromolecules 2020, 21, 4781–4794. [Google Scholar] [CrossRef] [PubMed]
- Nagarkar, R.P.; Schneider, J.P. Synthesis and Primary Characterization of Self-Assembled Peptide-Based Hydrogels. In Nanostructure Design: Methods and Protocols; Gazit, E., Nussinov, R., Eds.; Humana Press: Totowa, NJ, USA, 2008; pp. 61–77. [Google Scholar]
- Pitz, M.E.; Nukovic, A.M.; Elpers, M.A.; Alexander-Bryant, A.A. Factors Affecting Secondary and Supramolecular Structures of Self-Assembling Peptide Nanocarriers. Macromol. Biosci. 2022, 22, 2100347. [Google Scholar] [CrossRef]
- Yan, C.; Pochan, D.J. Rheological properties of peptide-based hydrogels for biomedical and other applications. Chem. Soc. Rev. 2010, 39, 3528–3540. [Google Scholar] [CrossRef]
- Meleties, M.; Britton, D.; Katyal, P.; Lin, B.; Martineau, R.L.; Gupta, M.K.; Montclare, J.K. High-Throughput Microrheology for the Assessment of Protein Gelation Kinetics. Macromolecules 2022, 55, 1239–1247. [Google Scholar] [CrossRef]
- Meleties, M.; Martineau, R.L.; Gupta, M.K.; Montclare, J.K. Particle-Based Microrheology As a Tool for Characterizing Protein-Based Materials. ACS Biomater. Sci. Eng. 2022, 8, 2747–2763. [Google Scholar] [CrossRef]
- Guilbaud, J.B.; Saiani, A. Using small angle scattering (SAS) to structurally characterise peptide and protein self-assembled materials. Chem. Soc. Rev. 2011, 40, 1200–1210. [Google Scholar] [CrossRef]
- McDowall, D.; Adams, D.J.; Seddon, A.M. Using small angle scattering to understand low molecular weight gels. Soft Matter 2022, 18, 1577–1590. [Google Scholar] [CrossRef]
- Hule, R.A.; Nagarkar, R.P.; Altunbas, A.; Ramay, H.R.; Branco, M.C.; Schneider, J.P.; Pochan, D.J. Correlations between structure, material properties and bioproperties in self-assembled β-hairpin peptide hydrogels. Faraday Discuss. 2008, 139, 251–264. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ran, Y.; Ge, Y.; Raza, F.; Li, S.; Zafar, H.; Wu, Y.; Paiva-Santos, A.C.; Yu, C.; Sun, M.; et al. pH-sensitive peptide hydrogels as a combination drug delivery system for cancer treatment. Pharmaceutics 2022, 14, 652. [Google Scholar] [CrossRef] [PubMed]
- Larsen, T.H.; Branco, M.C.; Rajagopal, K.; Schneider, J.P.; Furst, E.M. Sequence-dependent gelation kinetics of β-hairpin peptide hydrogels. Macromolecules 2009, 42, 8443–8450. [Google Scholar] [CrossRef]
- Haines-Butterick, L.; Rajagopal, K.; Branco, M.; Salick, D.; Rughani, R.; Pilarz, M.; Lamm, M.S.; Pochan, D.J.; Schneider, J.P. Controlling hydrogelation kinetics by peptide design for three-dimensional encapsulation and injectable delivery of cells. Proc. Natl. Acad. Sci. USA 2007, 104, 7791–7796. [Google Scholar] [CrossRef] [PubMed]
- Keiderling, T.A. Structure of condensed phase peptides: Insights from vibrational circular dichroism and Raman optical activity techniques. Chem. Rev. 2020, 120, 3381–3419. [Google Scholar] [CrossRef] [PubMed]
- Bajpayee, N.; Vijayakanth, T.; Rencus-Lazar, S.; Dasgupta, S.; Desai, A.V.; Jain, R.; Gazit, E.; Misra, R. Exploring Helical Peptides and Foldamers for the Design of Metal Helix Frameworks: Current Trends and Future Perspectives. Angew. Chem. 2023, 135, e202214583. [Google Scholar] [CrossRef]
- DiGuiseppi, D.; Kraus, J.; Toal, S.E.; Alvarez, N.; Schweitzer-Stenner, R. Investigating the formation of a repulsive hydrogel of a cationic 16mer peptide at low ionic strength in water by vibrational spectroscopy and rheology. J. Phys. Chem. B 2016, 120, 10079–10090. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Morris, K.; Laybourn, A.; Elias, D.; Hicks, M.R.; Rodger, A.; Serpell, L.; Adams, D.J. Self-assembly mechanism for a naphthalene- dipeptide leading to hydrogelation. Langmuir 2010, 26, 5232–5242. [Google Scholar] [CrossRef]
- Hu, G.; Pojman, J.A.; Scott, S.K.; Wrobel, M.M.; Taylor, A.F. Base-catalyzed feedback in the urea- urease reaction. J. Phys. Chem. B 2010, 114, 14059–14063. [Google Scholar] [CrossRef]
- Qin, Y.; Cabral, J.M. Kinetic studies of the urease-catalyzed hydrolysis of urea in a buffer-free system. Appl. Biochem. Biotechnol. 1994, 49, 217–240. [Google Scholar] [CrossRef]
- Heuser, T.; Weyandt, E.; Walther, A. Biocatalytic feedback-driven temporal programming of self-regulating peptide hydrogels. Angew. Chem. 2015, 127, 13456–13460. [Google Scholar] [CrossRef]
- Wrobel, M.M.; Bánsági, T.; Scott, S.K.; Taylor, A.F.; Bounds, C.O.; Carranza, A.; Pojman, J.A. pH wave-front propagation in the urea-urease reaction. Biophys. J. 2012, 103, 610–615. [Google Scholar] [CrossRef] [PubMed]
- Arosio, P.; Cukalevski, R.; Frohm, B.; Knowles, T.P.; Linse, S. Quantification of the concentration of Aβ42 propagons during the lag phase by an amyloid chain reaction assay. J. Am. Chem. Soc. 2014, 136, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Arosio, P.; Knowles, T.P.; Linse, S. On the lag phase in amyloid fibril formation. Phys. Chem. Chem. Phys. 2015, 17, 7606–7618. [Google Scholar] [CrossRef]
- Dudukovic, N.A.; Zukoski, C.F. Gelation of Fmoc-diphenylalanine is a first order phase transition. Soft Matter 2015, 11, 7663–7673. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, H.; Zhao, X. Mechanistic study of self-assembling peptide rada16-i in formation of nanofibers and hydrogels. J. Nanotechnol. Eng. Med. 2010, 1, 011007. [Google Scholar] [CrossRef]
- Emamyari, S.; Kargar, F.; Sheikh-Hasani, V.; Emadi, S.; Fazli, H. Mechanisms of the self-assembly of EAK16-family peptides into fibrillar and globular structures: Molecular dynamics simulations from nano-to micro-seconds. Eur. Biophys. J. 2015, 44, 263–276. [Google Scholar] [CrossRef]
- Pandya, M.J.; Spooner, G.M.; Sunde, M.; Thorpe, J.R.; Rodger, A.; Woolfson, D.N. Sticky-end assembly of a designed peptide fiber provides insight into protein fibrillogenesis. Biochemistry 2000, 39, 8728–8734. [Google Scholar] [CrossRef]
- Lara, C.; Adamcik, J.; Jordens, S.; Mezzenga, R. General self-assembly mechanism converting hydrolyzed globular proteins into giant multistranded amyloid ribbons. Biomacromolecules 2011, 12, 1868–1875. [Google Scholar] [CrossRef]
- Gurry, T.; Stultz, C.M. Mechanism of amyloid-β fibril elongation. Biochemistry 2014, 53, 6981–6991. [Google Scholar] [CrossRef]
- Scheidt, T.; Apińska, U.; Kumita, J.R.; Whiten, D.R.; Klenerman, D.; Wilson, M.R.; Cohen, S.I.; Linse, S.; Vendruscolo, M.; Dobson, C.M.; et al. Secondary nucleation and elongation occur at different sites on Alzheimer’s amyloid-β aggregates. Sci. Adv. 2019, 5, eaau3112. [Google Scholar] [CrossRef] [PubMed]
- Törnquist, M.; Michaels, T.C.; Sanagavarapu, K.; Yang, X.; Meisl, G.; Cohen, S.I.; Knowles, T.P.; Linse, S. Secondary nucleation in amyloid formation. Chem. Commun. 2018, 54, 8667–8684. [Google Scholar] [CrossRef] [PubMed]
- Maleki, M.; Natalello, A.; Pugliese, R.; Gelain, F. Fabrication of nanofibrous electrospun scaffolds from a heterogeneous library of co-and self-assembling peptides. Acta Biomater. 2017, 51, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Pugliese, R.; Maleki, M.; Zuckermann, R.N.; Gelain, F. Self-assembling peptides cross-linked with genipin: Resilient hydrogels and self-standing electrospun scaffolds for tissue engineering applications. Biomater. Sci. 2019, 7, 76–91. [Google Scholar] [CrossRef]
- Buzzaccaro, S.; Ruzzi, V.; Faleo, T.; Piazza, R. Microrheology of a thermosensitive gelling polymer for cell culture. J. Chem. Phys. 2022, 157, 174901. [Google Scholar] [CrossRef] [PubMed]
- Gelain, F.; Cigognini, D.; Caprini, A.; Silva, D.; Colleoni, B.; Donega, M.; Antonini, S.; Cohen, B.; Vescovi, A. New bioactive motifs and their use in functionalized self-assembling peptides for NSC differentiation and neural tissue engineering. Nanoscale 2012, 4, 2946–2957. [Google Scholar] [CrossRef]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; Mineola: Dover, NY, USA, 2000; Volume 376. [Google Scholar]
- Joosten, J.G.; McCarthy, J.L.; Pusey, P.N. Dynamic and static light scattering by aqueous polyacrylamide gels. Macromolecules 1991, 24, 6690–6699. [Google Scholar] [CrossRef]
- Pusey, P.N.; Van Megen, W. Dynamic light scattering by non-ergodic media. Phys. A Stat. Mech. Its Appl. 1989, 157, 705–741. [Google Scholar] [CrossRef]
- Usuelli, M.; Cao, Y.; Bagnani, M.; Handschin, S.; Nyström, G.; Mezzenga, R. Probing the structure of filamentous nonergodic gels by dynamic light scattering. Macromolecules 2020, 53, 5950–5956. [Google Scholar] [CrossRef]
- Duri, A.; Sessoms, D.A.; Trappe, V.; Cipelletti, L. Resolving long-range spatial correlations in jammed colloidal systems using photon correlation imaging. Phys. Rev. Lett. 2009, 102, 085702. [Google Scholar] [CrossRef]
- Secchi, E.; Roversi, T.; Buzzaccaro, S.; Piazza, L.; Piazza, R. Biopolymer gels with “physical” cross-links: Gelation kinetics, aging, heterogeneous dynamics, and macroscopic mechanical properties. Soft Matter 2013, 9, 3931–3944. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Gittings, A.; Suh, S.; Dixon, P.; Durian, D.J. Speckle-visibility spectroscopy: A tool to study time-varying dynamics. Rev. Sci. Instruments 2005, 76, 093110. [Google Scholar] [CrossRef]
- Piazza, R.; Campello, M.; Buzzaccaro, S.; Sciortino, F. Phase Behavior and Microscopic Dynamics of a Thermosensitive Gel-Forming Polymer. Macromolecules 2021, 54, 3897–3906. [Google Scholar] [CrossRef]
- Filiberti, Z.; Piazza, R.; Buzzaccaro, S. Multiscale relaxation in aging colloidal gels: From localized plastic events to system-spanning quakes. Phys. Rev. E 2019, 100, 042607. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buzzaccaro, S.; Ruzzi, V.; Gelain, F.; Piazza, R. A Light Scattering Investigation of Enzymatic Gelation in Self-Assembling Peptides. Gels 2023, 9, 347. https://doi.org/10.3390/gels9040347
Buzzaccaro S, Ruzzi V, Gelain F, Piazza R. A Light Scattering Investigation of Enzymatic Gelation in Self-Assembling Peptides. Gels. 2023; 9(4):347. https://doi.org/10.3390/gels9040347
Chicago/Turabian StyleBuzzaccaro, Stefano, Vincenzo Ruzzi, Fabrizio Gelain, and Roberto Piazza. 2023. "A Light Scattering Investigation of Enzymatic Gelation in Self-Assembling Peptides" Gels 9, no. 4: 347. https://doi.org/10.3390/gels9040347
APA StyleBuzzaccaro, S., Ruzzi, V., Gelain, F., & Piazza, R. (2023). A Light Scattering Investigation of Enzymatic Gelation in Self-Assembling Peptides. Gels, 9(4), 347. https://doi.org/10.3390/gels9040347