Assessment of Cavitation Models for Compressible Flows Inside a Nozzle
Abstract
:1. Introduction
2. Flow Configuration
3. Methodology
3.1. Mixture Model
3.2. Cavitation Models
3.2.1. Schnerr and Sauer (SS) Model
3.2.2. Zwart, Gerber, and Belamri (ZGB)
3.3. Liquid and Vapor Compressibility Models
3.3.1. Tait Equation
3.3.2. Ideal Gas Law
3.4. Sonic Speed in Mixture Phase Model
Wallis Sonic Speed in the Two-Phase System
4. Numerical Methods
5. Results and Discussion
5.1. Influence of Turbulence Modelling
5.2. Cavitation Model Assessment
5.3. Influence of Compressibility
6. Conclusions
- Four turbulence models were evaluated, the standard k-epsilon, realizable k-epsilon, Launder and Sharma k-epsilon, and SST k-omega. The results showed that turbulent viscosity profoundly affected the results, and that the realizable k-epsilon model was found to provide the most accurate results which is believed to be due to the formulation of turbulent viscosity.
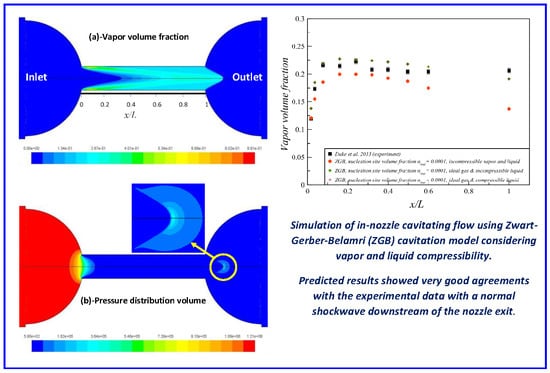
- The performance of the SS and ZGB cavitating models were analyzed and compared. The comparison of results showed higher vapor volume fraction when using the ZGB model because of the higher initial evaporation rate in the ZGB model, and lesser overall condensation rate with the ZGB model. The analyses also suggested that using incompressible liquid and vapor assumption, the models failed to capture the flow physics accurately.
- Simulations of the models with both liquid and vapor phase to be compressible showed that the SS model failed to predict the flow physics with a weak agreement with experimental data particularly in the nozzle core region, which is again believed to be due to the overestimation of condensation rate. However, the prediction results of the ZGB model were in better agreement with the experimental data and showed the ideal gas assumption allowed the cavitation vapor volume to change by the change in the local pressure. As a result, the cavitation vapor volume has been improved and increased compared to the incompressible assumption, particularly on the core region. In addition, a normal shockwave was predicted downstream of the cavitation region where the local sonic speed becomes subsonic from supersonic.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| speed of sound in the liquid phase | |
| speed of sound in the liquid-vapor mixture | |
| speed of sound in the vapor phase | |
| specific heat at constant pressure | |
| specific heat at constant volume | |
| cavitation number | |
| Nozzle diameter | |
| condensation coefficient | |
| evaporation coefficient | |
| reference bulk modulus | |
| bulk modulus | |
| L | Length of the nozzle |
| molecular weight | |
| density exponent | |
| bubble number density per unit volume of pure liquid | |
| bubble number density per unit volume of fluid mixture | |
| reference pressure | |
| pressure | |
| far-field pressure | |
| saturated vapor pressure | |
| saturation vapor pressure | |
| bubble radius | |
| bubble growth rate | |
| specific gas constant | |
| net phase change rate | |
| net condensation rate | |
| net evaporation rate | |
| universal gas constant | |
| Reynolds Number | |
| Temperature |
| liquid volume fraction | |
| vapor volume fraction | |
| nucleation site per volume fraction | |
| specific heat ratio | |
| molecular viscosity of the mixture | |
| molecular viscosity of the liquid | |
| molecular viscosity of the vapor | |
| reference density of liquid | |
| density of mixture | |
| density of the liquid | |
| density of the vapor | |
| mixture shear stress tensor |
References
- Karplus, H.B. Velocity of sound in a liquid containing gas bubbles. J. Acoust. Soc. Am. 1957, 29, 1261–1262. [Google Scholar] [CrossRef]
- Semenov, N.I.; Kosterin, S.I. Results of studying the speed of sound in moving gas-liquid systems. Teploenergetika 1964, 11, 46–51. [Google Scholar]
- Henry, R.E.; Grolmes, M.A.; Fauske, H.K. Pressure-Pulse Propagation in Two-Phase One-and Two-Component Mixtures. Technical Report No. ANL-7792; Argonne National Lab., Ill: Lemont, IL, USA, 1971. [Google Scholar] [CrossRef] [Green Version]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995; Volume 44. [Google Scholar]
- McWilliam, D.; Duggins, R.K. Speed of sound in bubbly liquids. Inst. Mech. Eng. Conf. Proc. 1969, 184, 102–107. [Google Scholar] [CrossRef]
- Soteriou, C.; Andrews, R.; Smith, M. Direct Injection Diesel Sprays and the Effect of Cavitation and Hydraulic Flip on Atomization. SAE Trans. 1995, 104, 128–153. [Google Scholar]
- Numachi, F.; Yamabe, M.; Oba, R. Cavitation Effect on the Discharge Coefficient of the Sharp-Edged Orifice Plate. ASME J. Basic Eng. 1960, 82, 1–6. [Google Scholar] [CrossRef]
- Yan, Y.; Thorpe, R.B. Flow regime transitions due to cavitation in the flow through an orifice. Int. J. Multiph. Flow 1990, 16, 1023–1045. [Google Scholar] [CrossRef]
- Simoneau, R.J. Pressure distribution in a converging-diverging nozzle during two-phase choked flow of subcooled nitrogen. In Proceedings of the Winter Animal Meeting of the American Society of Mechanical Engineers, Houston, TX, USA, 30 November–5 December 1975. Nasa Technical Report, 75N26306, Full Text. [Google Scholar]
- Simoneau, R.J.; Hendricks, R.C. Two-phase choked flow of cryogenic fluids in converging-diverging nozzles. NASA STI/Recon Tech. Rep. N 1979, 79, 29468. [Google Scholar]
- Waldrop, M.; Thomas, F. Video: Shock wave propagation: Cavitation of dodecane in a converging-diverging nozzle. In Proceedings of the 68th Annual meeting of APS Phys, Boston, MA, USA, 22–24 November 2015. [Google Scholar] [CrossRef]
- Winklhofer, E.; Kull, E.; Kelz, E.; Morozov, A. Comprehensive hydraulic and flow field documentation in model throttle experiments under cavitation conditions. In Proceedings of the ILASS-Europe 2001, 17 International Conference on Liquid Atomization and Spray Systems, Zurich, Switzerland, 2–6 September 2001. [Google Scholar] [CrossRef]
- Dorofeeva, I.; Thomas, F.; Dunn, P. Cavitation of JP-8 fuel in a converging-diverging nozzle: Experiments and modeling. In Proceedings of the 7th International Symposium on Cavitation, Ann Arbor, MI, USA, 17–22 August 2009. [Google Scholar]
- Battistoni, M.; Som, S.; Longman, D.E. Comparison of mixture and multifluid models for in-nozzle cavitation prediction. J. Eng. Gas Turbines Power 2014, 136, 61506. [Google Scholar] [CrossRef]
- Duke, D.; Kastengren, A.; Tilocco, F.Z.; Powell, C. Synchrotron x-ray measurements of cavitation. In Proceedings of the 25th Annual Conference on Liquid Atomization and Spray Systems, ILASS-Americas, Pittsburgh, PA, USA, 21–23 May 2013; pp. 5–8. [Google Scholar]
- Schmidt, D.P.; Gopalakrishnan, S.; Jasak, H. Multi-dimensional simulation of thermal non-equilibrium channel flow. Int. J. Multiph. Flow 2010, 36, 284–292. [Google Scholar] [CrossRef]
- Bilicki, Z.; Kestin, J. Physical aspects of the relaxation model in two-phase flow. R. Soc. London A Math. Phys. Eng. Sci. 1990, 428, 379–397. [Google Scholar]
- Brennen, C.E. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Manninen, M.; Taivassalo, V.; Kallio, S. On the Mixture Model for Multiphase Flow; VTT Publications 288: Espoo, Finland, 1996. [Google Scholar]
- Battistoni, M.; Grimaldi, C.N. Analysis of transient cavitating flows in diesel injectors using diesel and biodiesel fuels. SAE Int. J. Fuels Lubr. 2010, 3, 2010-01-2245. [Google Scholar] [CrossRef]
- Rayleigh, L., VIII. On the pressure developed in a liquid during the collapse of a spherical cavity. London, Edinburgh, Dublin Philos. Mag. J. Sci. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Drew, D.A.; Passman, S.L. Theory of Multicomponent Fluids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 135. [Google Scholar]
- Cristofaro, M.; Edelbauer, W.; Koukouvinis, P.; Gavaises, M. Influence of Diesel Fuel Viscosity on Cavitating Throttle Flow Simulations under Erosive Operation Conditions. ACS Omega 2020, 5, 7182–7192. [Google Scholar] [CrossRef] [PubMed]
- Grogger, H.A.; Alajbegovic, A. Calculation of the cavitating flow in venturi geometries using two-fluid model. In Proceedings of the SME Proceeding, FEDSM’98, Washington, DC, USA, 21–25 June 1998; p. 5295. [Google Scholar]
- Kobayashi, H. The subgrid-scale models based on coherent structures for rotating homogeneous turbulence and turbulent channel flow. Phys. Fluids 2005, 17, 45104. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and numerical modelling of unsteady cavitation dynamics. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001; Volume 1. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Dymond, J.H.; Malhotra, R. The Tait equation: 100 years on. Int. J. Thermophys. 1988, 9, 941–951. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Gavaises, M.; Li, J.; Wang, L. Large Eddy Simulation of Diesel injector including cavitation effects and correlation to erosion damage. Fuel 2016, 175, 26–39. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Irawan, D.; García, A.; Gutiérrez, A.J.; Álvarez, E.; Blanco, E. Modeling of coil cooling using 2D and 3D computational fluid dynamics (CFD). In Proceedings of the 3rd International Congress on Water, Waste and Energy Management, Rome, Italy, 18–20 July 2016. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-epsilon eddy viscosity model for high Reynolds number turbulent flows: Model development and validation. ScienceDirect 1995, 24, 227–238. [Google Scholar]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–137. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Bauer, D.; Chaves, H.; Arcoumanis, C. Measurements of void fraction distribution in cavitating pipe flow using x-ray CT. Meas. Sci. Technol. 2012, 23, 55302. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Sauer, J.; Schnerr, G.H. Modeling and computation of unsteady cavitation flows in injection nozzles. Méc. Ind. 2001, 2, 383–394. [Google Scholar] [CrossRef]
- Ivings, M.J.; Causon, D.M.; Toro, E.F. On Riemann solvers for compressible liquids. Int. J. Numer. Methods Fluids 1998, 28, 395–418. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent 14.5 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- McCain, W.D., Jr. Properties of Petroleum Fluids; PennWell Corporation: Tulsa, OK, USA, 2017. [Google Scholar]
- Wallis, G.B. One-Dimensional Two-Phase Flow; McGraw-Hill: New York, NY, USA, 1969; Volume 1. [Google Scholar]
- Srinivasan, V.; Salazar, A.; Saito, K. Numerical simulation of cavitation dynamics using a cavitation-induced-momentum-defect (CIMD) correction approach. Appl. Math. Model. 2009, 33, 1529–1559. [Google Scholar] [CrossRef]
- Schmidt, D.P.; Rutland, C.J.; Corradini, M.L. A fully compressible, two-dimensional model of small, high-speed, cavitating nozzles. At. Sprays 1999, 9, 255–276. [Google Scholar] [CrossRef]
- Kader, B.A. Temperature and concentration profiles in fully turbulent boundary layers. Int. J. Heat Mass Transf. 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Sauer, J.; Schnerr, G.H. Unsteady Cavitating Flow: A New Cavitation Model Based on Modified Front Capturing Method and Bubble Dynamics. In Proceedings of the 2000 ASME Fluids Engineering Division summer meeting, Boston, MA, USA, 11–15 June 2000; pp. 1073–1080. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. Trans. Soc. Mech. Eng. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Martynov, S.B.; Mason, D.J.; Heikal, M.R. Numerical simulation of cavitation flows based on their hydrodynamic similarity. Int. J. Engine Res. 2006, 7, 283–296. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A. Investigation of in-Nozzle Flow Characteristics of Fuel Injectors of IC Engines. Ph.D. Thesis, University of London, London, UK, 2017. [Google Scholar]

















| Fuel Flow Rate [L/hr] | Reynolds Number, Re | Cavitation Number, CN | T [°C] | ||
|---|---|---|---|---|---|
| 1060 ± 60 | 87 ± 2 | 26.8 ± 0.24 | 15,800 | 11.2 | 25 |
| 101,325 | 777.97 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Ghobadian, A.; Nouri, J.M. Assessment of Cavitation Models for Compressible Flows Inside a Nozzle. Fluids 2020, 5, 134. https://doi.org/10.3390/fluids5030134
Kumar A, Ghobadian A, Nouri JM. Assessment of Cavitation Models for Compressible Flows Inside a Nozzle. Fluids. 2020; 5(3):134. https://doi.org/10.3390/fluids5030134
Chicago/Turabian StyleKumar, Aishvarya, Ali Ghobadian, and Jamshid M. Nouri. 2020. "Assessment of Cavitation Models for Compressible Flows Inside a Nozzle" Fluids 5, no. 3: 134. https://doi.org/10.3390/fluids5030134
APA StyleKumar, A., Ghobadian, A., & Nouri, J. M. (2020). Assessment of Cavitation Models for Compressible Flows Inside a Nozzle. Fluids, 5(3), 134. https://doi.org/10.3390/fluids5030134