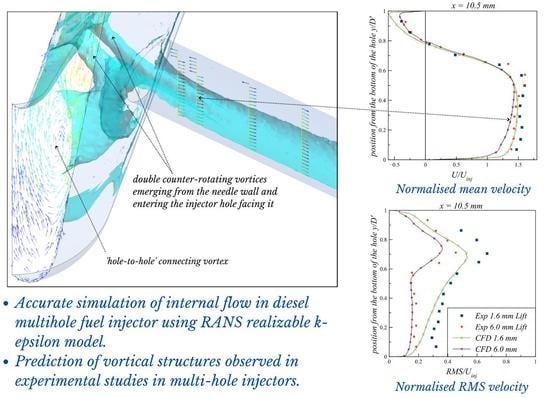
Predictions of Vortex Flow in a Diesel Multi-Hole Injector Using the RANS Modelling Approach
Abstract
:1. Introduction
2. Flow Configuration
3. Methodology
3.1. Governing Equations
3.2. Turbulence Model
4. Numerical Methods
5. Results and Discussion
5.1. Validation of Simulation Results
5.2. Flow Field Analysis
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| = Cavitation number | Non-dimensional number |
| = Diameter of an injector hole | Mm |
| = Turbulent kinetic energy | m2s−2 |
| Number of injector holes | Non-dimensional number |
| = Pressure | Pa |
| = Mean pressure | Pa |
| Injection pressure | Pa |
| = Back (downstream) pressure | Pa |
| = Saturated vapour pressure | Pa |
| Volumetric flow rate | m3s−1 |
| = Reynolds number | Non-dimensional number |
| = Mean rate of strain tensor | s−1 |
| = Fluctuating rate of strain tensor | s−1 |
| = Temperature | K |
| = Velocity in the ith direction | ms−1 |
| = Mean velocity in the ith direction | ms−1 |
| = Fluctuating velocity component in the direction | ms−1 |
| Greek Symbols | |
| = Epsilon | m2s−3 |
| = Kronecker delta | Non-dimensional number |
| = Molecular viscosity of the fluid | Pa·s−1 |
| = Turbulent viscosity | Pa·s−1 |
| = Kinematic viscosity of the fluid | m2s−1 |
| = Kinematic viscosity of the liquid | m2s−1 |
| = Density | kg·m−3 |
| = Mean rate of rotation tensor | s−1 |
| = Angular velocity | rad·s−1 |
| Abbreviations | |
| CT | Computed tomography |
| CCD | Charge-coupled device |
| DES | Detached-eddy simulation |
| LDV | Laser Doppler velocimetry |
| LES | Large-eddy simulation |
| RANS | Reynolds-averaged Navier–Stokes |
| RMS | Root mean square |
Appendix A. Grid Independence Study at Low Lift
| Grid | Number of Cells | |
|---|---|---|
| 1 | 1,792,278 | 17.7 |
| 2 | 6,892,758 | 10.44 |
| 3 | 11,049,454 | 9.54 |
| 4 | 19,023,384 | 7.5 |
| 5 | 16,410,517 | 7.21 |
| 6 | 21,216,968 | 7.14 |
| 7 | 33,446,472 | 7.16 |


References
- Zhao, H. Advanced Direct Injection Combustion Engine Technologies and Development: Diesel Engines; Elsevier: Amsterdam, The Netherlands, 2009; Volume 2. [Google Scholar]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Soteriou, C.; Andrews, R.; Smith, M. Direct Injection Diesel Sprays and the Effect of Cavitation and Hydraulic Flip on Atomization. SAE Trans. 1995, 104, 128–153. [Google Scholar]
- Arcoumanis, C.; Gavaises, M.; Nouri, J.M.; Abdul-Wahab, E.; Horrocks, R.W. Analysis of the Flow in the Nozzle of a Vertical Multi-Hole Diesel Engine Injector. SAE Trans. 1998, 1245–1259. [Google Scholar] [CrossRef]
- Afzal, H.; Arcoumanis, C.; Gavaises, M.; Kampanis, N. Internal Flow in Diesel Injector Nozzles: Modelling and Experiments. IMechE Pap. S 1999, 492, 25–44. [Google Scholar]
- Arcoumanis, C.; Flora, H.; Gavaises, M.; Kampanis, N.; Horrocks, R. Investigation of Cavitation in a Vertical Multi-Hole Injector. SAE Trans. 1999, 108, 661–678. [Google Scholar]
- Arcoumanis, C.; Gavaises, M.; Nouri, J.M. The role of cavitation in automotive fuel injection systems. In Proceedings of the 8th International Symposium on Internal Combustion Diagnostics, Baden-Baden, Germany, 10–11 June 2008; pp. 159–167. [Google Scholar]
- Roth, H.; Gavaises, M.; Arcoumanis, C. Cavitation Initiation, Its Development and Link with Flow Turbulence in Diesel Injector Nozzles. SAE Trans. 2002, 111, 561–580. [Google Scholar]
- Mitroglou, N.; Nouri, J.M.; Gavaises, M.; Arcoumanis, C. Spray Characteristics of a Multi-Hole Injector for Direct-Injection Gasoline Engines. Int. J. Engine Res. 2006, 7, 255–270. [Google Scholar] [CrossRef] [Green Version]
- Mitroglou, N.; Gavaises, M.; Nouri, J.M.; Arcoumanis, C. Cavitation inside Enlarged and Real-Size Fully Transparent Injector Nozzles and Its Effect on near Nozzle Spray Formation. In Proceedings of the DIPSI Workshop 2011, Droplet Impact Phenomena & Spray Investigations, Bergamo, Italy, 27 May 2011; pp. 33–45. [Google Scholar]
- Mirshahi, M.; Nouri, J.M.; Yan, Y.; Gavaises, M. Link between In-Nozzle Cavitation and Jet Spray in a Gasoline Multi-Hole Injector. In Proceedings of the ILASS-Europe, 25th European Conference on Liquid Atomization and Spray Systems, Chania, Greece, 1–4 September 2013. [Google Scholar]
- Kumar, A.; Ghobadian, A.; Nouri, J.M. Assessment of Cavitation Models for Compressible Flows Inside a Nozzle. Fluids 2020, 5, 134. [Google Scholar] [CrossRef]
- Kumar, A.; Ghobadian, A.; Nouri, J. Numerical Simulation and Experimental Validation of Cavitating Flow in a Multi-Hole Diesel Fuel Injector. Int. J. Engine Res. 2021. [Google Scholar] [CrossRef]
- Giannadakis, E.; Gavaises, M.; Roth, H.; Arcoumanis, C. Cavitation Modelling in Single-Hole Diesel Injector Based on Eulerian-Lagrangian Approach. In Proceedings of the THIESEL International Conference on Thermo-and Fluid Dynamic Processes in Diesel Engines, Valencia, Spain, 7–10 September 2004. [Google Scholar]
- Giannadakis, E.; Gavaises, M.; Arcoumanis, C. Modelling of Cavitation in Diesel Injector Nozzles. J. Fluid Mech. 2008, 616, 153–193. [Google Scholar] [CrossRef] [Green Version]
- Papoutsakis, A.; Theodorakakos, A.; Giannadakis, E.; Papoulias, D.; Gavaises, M. LES Predictions of the Vortical Flow Structures in Diesel Injector Nozzles. SAE Tech. Pap. 2009. [Google Scholar] [CrossRef]
- Sou, A.; Biçer, B.; Tomiyama, A. Numerical Simulation of Incipient Cavitation Flow in a Nozzle of Fuel Injector. Comput. Fluids 2014, 103, 42–48. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Naseri, H.; Gavaises, M. Performance of Turbulence and Cavitation Models in Prediction of Incipient and Developed Cavitation. Int. J. Engine Res. 2017, 18, 333–350. [Google Scholar] [CrossRef]
- Karathanassis, I.K.; Hwang, J.; Koukouvinis, P.; Pickett, L.; Gavaises, M. Combined visualisation of cavitation and vortical structures in a real-size optical diesel injector. Exp. Fluids 2021, 62. [Google Scholar] [CrossRef]
- Kolovos, K.; Kyriazis, N.; Koukouvinis, P.; Vidal, A.; Gavaises, G.; McDavid, R.M. Simulation of transient effects in a fuel injector nozzle using real-fluid thermodynamic closure. Appl. Energy Combust. Sci. 2021, 7, 100037. [Google Scholar] [CrossRef]
- Mamaikin, D.; Knorsch, T.; Rogler, P.; Wang, J.; Wensing, M. The effect of transient needle lift on the internal flow and near-nozzle spray characteristics for modern GDI systems investigated by high-speed X-ray imaging. Int. J. Engine Res. 2021. [Google Scholar] [CrossRef]
- Strotos, G.; Koukouvinis, P.; Theodorakakos, A.; Gavaises, M.; Bergeles, G. Transient heating effects in high pressure Diesel injector nozzles. Int. J. Heat Fluid Flow 2015, 51, 257–267. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada Flintridge, CA, USA, 1998; Volume 2, ISBN 0963605151. [Google Scholar]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New K-Epsilon Eddy Viscosity Model for High Reynolds Number Turbulent Flows: Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Kumar, A. Investigation of In-Nozzle Flow Characteristics of Fuel Injectors of IC Engines. Ph.D. Thesis, City, University of London, London, UK, 2017. [Google Scholar] [CrossRef]
- Nouri, J.M.; Whitelaw, J.H.; Yianneskis, M. A Refractive-Index Matching Technique for Solid/Liquid Flows. Laser Anemometry Fluid Mech. 1988, 3, 335. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Alfonsi, G. Reynolds-Averaged Navier–Stokes Equations for Turbulence Modeling. Appl. Mech. Rev. 2009, 62. [Google Scholar] [CrossRef]
- Schumann, U. Realizability of Reynolds—Stress Turbulence Models. Phys. Fluids 1977, 20, 721–725. [Google Scholar] [CrossRef]
- Lumley, J.L. Computational modeling of turbulent flows. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 18, pp. 123–176. ISBN 0065-2156. [Google Scholar]
- Fluent, A. 14.5 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980; ISBN 9781315275130. [Google Scholar]
- Kader, B.A. Temperature and Concentration Profiles in Fully Turbulent Boundary Layers. Int. J. Heat Mass Transf. 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Hanjalic, K. Will RANS survive LES? A View of Perspectives. J. Fluids Eng. 2005, 127, 831–839. [Google Scholar] [CrossRef]













| Case | Series | Needle Lift (mm) | (bar) | (bar) | (m/s) | Volumetric Flow Rate Qt (L/s) | Temperature (°C) | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.6 (low) | 0.45 | 18,000 | 2.55 | 1.80 | 8.43 | 0.487 | 25 ± 0.5 |
| 2 | 1.6 (low) | 0.45 | 18,000 | 2.55 | 1.80 | 8.43 | 0.487 | 25 ± 0.5 | |
| 2 | 1 | 6.0 (full) | 0.44 | 21,000 | 1.80 | 1.27 | 9.84 | 0.568 | 25 ± 0.5 |
| 2 | 6.0 (full) | 0.44 | 21,000 | 1.80 | 1.27 | 9.84 | 0.568 | 25 ± 0.5 |
| Case | Needle Lift | (1) * Inlet (Mass Flow Rate) | (2) * Outlet (Constant Pressure) | (3) * Walls | (4) * Interface (Rotational Periodic) |
|---|---|---|---|---|---|
| 1 | 1.6 mm (lower) | 0.0726 kg/s | 180,000 N/m2 | No-slip | 60 |
| 2 | 6.0 mm (full) | 0.0847 kg/s | 127,000 N/m2 | No-slip | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Nouri, J.; Ghobadian, A. Predictions of Vortex Flow in a Diesel Multi-Hole Injector Using the RANS Modelling Approach. Fluids 2021, 6, 421. https://doi.org/10.3390/fluids6120421
Kumar A, Nouri J, Ghobadian A. Predictions of Vortex Flow in a Diesel Multi-Hole Injector Using the RANS Modelling Approach. Fluids. 2021; 6(12):421. https://doi.org/10.3390/fluids6120421
Chicago/Turabian StyleKumar, Aishvarya, Jamshid Nouri, and Ali Ghobadian. 2021. "Predictions of Vortex Flow in a Diesel Multi-Hole Injector Using the RANS Modelling Approach" Fluids 6, no. 12: 421. https://doi.org/10.3390/fluids6120421
APA StyleKumar, A., Nouri, J., & Ghobadian, A. (2021). Predictions of Vortex Flow in a Diesel Multi-Hole Injector Using the RANS Modelling Approach. Fluids, 6(12), 421. https://doi.org/10.3390/fluids6120421