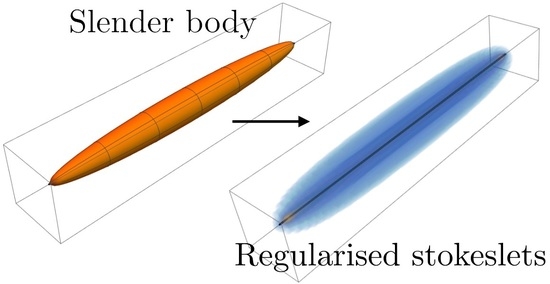
Regularized Stokeslets Lines Suitable for Slender Bodies in Viscous Flow
Abstract
:1. Introduction
2. Background into Viscous Flows around Slender Bodies
2.1. Stokes Flow and Classical Singularity Solutions
2.2. Regularized Singularity Solutions
2.3. Classical Slender-Body Theory
2.4. Regularized Slender-Body Theories
3. Regularizations for the Flow Far from a Slender Body
4. Regularization’s for the Flow Near a Slender Body
5. Testing the Conditions on Common Blob Types
5.1. Power-Law Blobs
5.2. Compact Blobs
5.3. Gaussian Blobs
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cox, R.G. The motion of long slender bodies in a viscous fluid Part 1. General theory. J. Fluid Mech. 1970, 44, 791. [Google Scholar] [CrossRef]
- Lighthill, J. Flagellar Hydrodynamics: The John von Neumann Lecture, 1975. SIAM Rev. 1976, 18, 161–230. [Google Scholar] [CrossRef]
- Batchelor, G.K. Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 1970, 44, 419–440. [Google Scholar] [CrossRef]
- Keller, J.B.; Rubinow, S.I. Slender-body theory for slow viscous flow. J. Fluid Mech. 1976, 75, 705–714. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.E. An improved slender-body theory for Stokes flow. J. Fluid Mech. 1979, 99, 411–431. [Google Scholar] [CrossRef]
- Götz, T. Interactions of Fibers and Flow: Asymptotics, Theory and Numerics. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 2000. [Google Scholar]
- Koens, L.; Lauga, E. The boundary integral formulation of Stokes flows includes slender-body theory. J. Fluid Mech. 2018, 850, R1. [Google Scholar] [CrossRef] [Green Version]
- Andersson, H.I.; Celledoni, E.; Ohm, L.; Owren, B.; Tapley, B.K. An integral model based on slender body theory, with applications to curved rigid fibers. Phys. Fluids 2021, 33, 041904. [Google Scholar] [CrossRef]
- Barta, E.; Liron, N. Slender Body Interactions for Low Reynolds Numbers—Part I: Body-Wall Interactions. SIAM J. Appl. Math. 1988, 48, 992–1008. [Google Scholar] [CrossRef]
- Koens, L.; Montenegro-Johnson, T.D. Local drag of a slender rod parallel to a plane wall in a viscous fluid. Phys. Rev. Fluids 2021, 6, 064101. [Google Scholar] [CrossRef]
- Kim, M.J.; Kim, M.J.; Bird, J.C.; Park, J.; Powers, T.R.; Breuer, K.S. Particle image velocimetry experiments on a macro-scale model for bacterial flagellar bundling. Exp. Fluids 2004, 37, 782–788. [Google Scholar] [CrossRef]
- Das, D.; Lauga, E. Computing the motor torque of Escherichia coli. Soft Matter 2018, 14, 5955–5967. [Google Scholar] [CrossRef] [Green Version]
- Higdon, J.J.L. A hydrodynamic analysis of flagellar propulsion. J. Fluid Mech. 1979, 90, 685. [Google Scholar] [CrossRef]
- Barta, E.; Weihs, D. Creeping flow around a finite row of slender bodies in close proximity. J. Fluid Mech. 2006, 551, 1–17. [Google Scholar] [CrossRef]
- Cummins, C.; Seale, M.; Macente, A.; Certini, D.; Mastropaolo, E.; Viola, I.M.; Nakayama, N. A separated vortex ring underlies the flight of the dandelion. Nature 2018, 562, 414–418. [Google Scholar] [CrossRef]
- Rodenborn, B.; Chen, C.H.; Swinney, H.L.; Liu, B.; Zhang, H.P. Propulsion of microorganisms by a helical flagellum. Proc. Natl. Acad. Sci. USA 2013, 110, E338–E347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gray, J.; Hancock, G.J. The Propulsion of Sea-Urchin Spermatozoa. J. Exp. Biol. 1955, 32, 802–814. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Moldovan, R.; Yeung, C.; Wu, X. Swimming efficiency of bacterium Escherichia coli. Proc. Natl. Acad. Sci. USA 2006, 103, 13712–13717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koens, L.; Zhang, H.; Moeller, M.; Mourran, A.; Lauga, E. The swimming of a deforming helix. Eur. Phys. J. E 2018, 41, 119. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chan, F.K.; Parthasarathy, T.; Gazzola, M. Modeling and simulation of complex dynamic musculoskeletal architectures. Nat. Commun. 2019, 10, 4825. [Google Scholar] [CrossRef] [Green Version]
- Becker, L.E.; Koehler, S.A.; Stone, H.A. On self-propulsion of micro-machines at low Reynolds number: Purcell’s three-link swimmer. J. Fluid Mech. 2003, 490, 15–35. [Google Scholar] [CrossRef] [Green Version]
- Tătulea-Codrean, M.; Lauga, E. Asymptotic theory of hydrodynamic interactions between slender filaments. Phys. Rev. Fluids 2021, 6, 074103. [Google Scholar] [CrossRef]
- Waszkiewicz, R.; Szymczak, P.; Lisicki, M. Stability of sedimenting flexible loops. J. Fluid Mech. 2021, 919, A14. [Google Scholar] [CrossRef]
- Man, Y.; Page, W.; Poole, R.J.; Lauga, E. Bundling of elastic filaments induced by hydrodynamic interactions. Phys. Rev. Fluids 2017, 2, 123101. [Google Scholar] [CrossRef] [Green Version]
- Cortez, R. The Method of Regularized Stokeslets. SIAM J. Sci. Comput. 2001, 23, 1204–1225. [Google Scholar] [CrossRef]
- Cortez, R.; Fauci, L.; Medovikov, A. The method of regularized Stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys. Fluids 2005, 17, 031504. [Google Scholar] [CrossRef]
- Zhao, B.; Lauga, E.; Koens, L. Method of regularized stokeslets: Flow analysis and improvement of convergence. Phys. Rev. Fluids 2019, 4, 084104. [Google Scholar] [CrossRef]
- Smith, D.J. A boundary element regularized Stokeslet method applied to cilia- and flagella-driven flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 3605–3626. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, M.T.; Smith, D.J. The art of coarse Stokes: Richardson extrapolation improves the accuracy and efficiency of the method of regularized stokeslets. R. Soc. Open Sci. 2021, 8, 210108. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.N.; Cortez, R. Reduction of the Regularization Error of the Method of Regularized Stokeslets for a Rigid Object Immersed in a Three-Dimensional Stokes Flow. Commun. Comput. Phys. 2014, 15, 126–152. [Google Scholar] [CrossRef]
- Walker, B.J.; Curtis, M.P.; Ishimoto, K.; Gaffney, E.A. A regularised slender-body theory of non-uniform filaments. J. Fluid Mech. 2020, 899, A3. [Google Scholar] [CrossRef]
- Cortez, R.; Nicholas, M. Slender body theory for Stokes flows with regularized forces. Commun. Appl. Math. Comput. Sci. 2012, 7, 33–62. [Google Scholar] [CrossRef] [Green Version]
- Cortez, R. Regularized Stokeslet segments. J. Comput. Phys. 2018, 375, 783–796. [Google Scholar] [CrossRef] [Green Version]
- Buchmann, A.; Fauci, L.J.; Leiderman, K.; Strawbridge, E.; Zhao, L. Mixing and pumping by pairs of helices in a viscous fluid. Phys. Rev. E 2018, 97, 023101. [Google Scholar] [CrossRef] [Green Version]
- Martindale, J.D.; Jabbarzadeh, M.; Fu, H.C. Choice of computational method for swimming and pumping with nonslender helical filaments at low Reynolds number. Phys. Fluids 2016, 28, 021901. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.; Cortez, R.; Fauci, L. Computing Flows Around Microorganisms: Slender-Body Theory and Beyond. Am. Math. Mon. 2014, 121, 810. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.; Koehl, M.A.R.; Oakes, C.; Bustamante, G.; Fauci, L. Effects of cell morphology and attachment to a surface on the hydrodynamic performance of unicellular choanoflagellates. J. R. Soc. Interface 2019, 16, 20180736. [Google Scholar] [CrossRef] [Green Version]
- Bouzarth, E.L.; Hutson, K.R.; Miller, Z.L.; Saine, M.E. Using Regularized Singularities to Model Stokes Flow: A Study of Fluid Dynamics Induced by Metachronal Ciliary Waves. In An Introduction to Undergraduate Research in Computational and Mathematical Biology. Foundations for Undergraduate Research in Mathematics; Birkhäuser: Cham, Switzerland, 2020; pp. 443–469. [Google Scholar] [CrossRef]
- Olson, S.D.; Suarez, S.S.; Fauci, L.J. Coupling biochemistry and hydrodynamics captures hyperactivated sperm motility in a simple flagellar model. J. Theor. Biol. 2011, 283, 203–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montenegro-Johnson, T.D.; Koens, L.; Lauga, E. Microscale flow dynamics of ribbons and sheets. Soft Matter 2017, 13, 546–553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ohm, L. Remarks on Regularized Stokeslets in Slender Body Theory. Fluids 2021, 6, 283. [Google Scholar] [CrossRef]
- Kim, S.; Karrila, S.J. Microhydrodynamics: Principles and Selected Applications; Courier Corporation: Boston, MA, USA, 2005; p. 507. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932; p. 605. [Google Scholar]
- Pozrikidis, C. Boundary Integral and Singularity Methods for Linearized Viscous Flow; Cambridge University Press: Cambridge, UK, 1992; p. 259. [Google Scholar]
- Chwang, A.T.; Wu, T.Y. Hydromechanics of low-Reynolds-number flow. Part 2. Singularity method for Stokes flows. J. Fluid Mech. 1975, 67, 787–815. [Google Scholar] [CrossRef] [Green Version]
- Montenegro-Johnson, T.; Smith, A.; Smith, D.; Loghin, D.; Blake, J. Modelling the fluid mechanics of cilia and flagella in reproduction and development. Eur. Phys. J. E Soft Matter 2012, 35, 111. [Google Scholar] [CrossRef] [Green Version]
- Montenegro-Johnson, T.D. Microtransformers: Controlled microscale navigation with flexible robots. Phys. Rev. Fluids 2018, 3, 062201. [Google Scholar] [CrossRef] [Green Version]
- Ainley, J.; Durkin, S.; Embid, R.; Boindala, P.; Cortez, R. The method of images for regularized Stokeslets. J. Comput. Phys. 2008, 227, 4600–4616. [Google Scholar] [CrossRef]
- Cortez, R.; Varela, D. A general system of images for regularized Stokeslets and other elements near a plane wall. J. Comput. Phys. 2015, 285, 41–54. [Google Scholar] [CrossRef]
- Hinch, E.J. Perturbation Methods; Cambridge University Press: Cambridge, UK, 1991; p. 160. [Google Scholar]
- Lauga, E. Bacterial Hydrodynamics. Annu. Rev. Fluid Mech. 2016, 48, 105–130. [Google Scholar] [CrossRef] [Green Version]
- Gaffney, E.A.; Gadêlha, H.; Smith, D.J.; Blake, J.R.; Kirkman-Brown, J.C. Mammalian Sperm Motility: Observation and Theory. Annu. Rev. Fluid Mech. 2011, 43, 501–528. [Google Scholar] [CrossRef] [Green Version]
- Katsamba, P.; Michelin, S.; Montenegro-Johnson, T.D. Slender Phoretic Theory of chemically active filaments. J. Fluid Mech. 2020, 898, A24. [Google Scholar] [CrossRef]
- Borker, N.S.; Koch, D.L. Slender body theory for particles with non-circular cross-sections with application to particle dynamics in shear flows. J. Fluid Mech. 2019, 877, 1098–1133. [Google Scholar] [CrossRef] [Green Version]
- Koens, L.; Lauga, E. Slender-ribbon theory. Phys. Fluids 2016, 28, 013101. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; Ohm, L. Accuracy of slender body theory in approximating force exerted by thin fiber on viscous fluid. Stud. Appl. Math. 2021, 147, 127–179. [Google Scholar] [CrossRef]
- Mori, Y.; Ohm, L.; Spirn, D. Theoretical Justification and Error Analysis for Slender Body Theory. Commun. Pure Appl. Math. 2020, 73, 1245–1314. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; Ohm, L.; Spirn, D. Theoretical Justification and Error Analysis for Slender Body Theory with Free Ends. Arch. Ration. Mech. Anal. 2020, 235, 1905–1978. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Koens, L. Regularized Stokeslets Lines Suitable for Slender Bodies in Viscous Flow. Fluids 2021, 6, 335. https://doi.org/10.3390/fluids6090335
Zhao B, Koens L. Regularized Stokeslets Lines Suitable for Slender Bodies in Viscous Flow. Fluids. 2021; 6(9):335. https://doi.org/10.3390/fluids6090335
Chicago/Turabian StyleZhao, Boan, and Lyndon Koens. 2021. "Regularized Stokeslets Lines Suitable for Slender Bodies in Viscous Flow" Fluids 6, no. 9: 335. https://doi.org/10.3390/fluids6090335
APA StyleZhao, B., & Koens, L. (2021). Regularized Stokeslets Lines Suitable for Slender Bodies in Viscous Flow. Fluids, 6(9), 335. https://doi.org/10.3390/fluids6090335